基于Copula-Monte Carlo法的水庫下游洪水概率分布研究

劉章君，郭生練，胡 瑤，楊 光，尹家波

(武漢大學水資源與水電工程科學國家重點實驗室，湖北武漢430072)

基于Copula-Monte Carlo法的水庫下游洪水概率分布研究

劉章君，郭生練，胡 瑤，楊 光，尹家波

(武漢大學水資源與水電工程科學國家重點實驗室，湖北武漢430072)

利用Copula函數構造水庫調洪控制時段洪量和區間洪峰的聯合分布，通過調洪函數將水庫入庫洪量轉換為下泄洪峰，隨機模擬得到兩分區洪峰流量，提出了推求水庫下游洪水概率分布的Copula-Monte Carlo(Copula-MC)方法。應用清江流域隔河巖水庫實例進行驗證，推求下游高壩洲斷面的洪水概率分布，并與忽略洪水相關性的獨立MC法進行比較，結果表明，獨立MC法計算的洪峰流量系統偏小，會低估高壩洲斷面的防洪風險；Copula-MC法得到的100年一遇高壩洲斷面設計洪水與天然情況下相比減小32.6%。Copula-MC法充分考慮了上游水庫斷面和區間洪水的空間相關性及地區組成的隨機性，結果合理可行。

水庫調蓄；概率分布；Copula函數；Copula-Monte Carlo法；清江流域

0 引 言

設計斷面的洪水概率分布是對其洪水情勢的統計描述，是各類水利水電工程規劃設計中的重要依據。河流上游調蓄作用較大的水庫對洪水具有調節作用，改變了下游天然洪水的時程分配及峰、量，從而影響下游洪水的概率分布。研究上游水庫如何進行設計才能滿足下游設計斷面的防洪要求，或者當水庫的泄洪設施規模、防洪庫容等參數確定時，水庫對下游設計斷面的影響等問題，都需要研究受水庫調洪影響后下游洪水的概率分布問題[1- 2]。

目前的計算方法可以分為“自下而上”和“自上而下”兩大類。前者通過擬定設計斷面設計洪水的地區組成，即將設計斷面設計洪量分配給上游各分區以研究水庫的調洪影響。選擇科學合理的分配規則來分配設計洪量是此類方法的關鍵。由于各分區洪水有一定的相關性，其相互遭遇組合具有明顯的隨機性，給實際分析帶來了很大的困難。學者們先后提出了典型年法和同頻率地區組成法兩種常用方法[1- 2]及最近的JC法[3- 4]和Copula函數法[5- 7]等洪量分配規則。然而，這類方法簡單地假定水庫調蓄后設計斷面的洪水與天然情況同頻率，沒有充分考慮洪水地區組成的隨機特性和水庫的調洪影響。后者則較好地克服了上述問題，它不去研究如何分配設計斷面的設計洪量，而是研究上游各分區洪水所有可能的組合遭遇情況，能夠反映水庫對不同頻率洪水的調洪效應。該類方法按照處理方式的不同主要包括概率組合離散求和法和隨機模擬法[1- 2]。由于上游水庫斷面和區間洪水通常具有空間相關性，使得離散求和法往往受到聯合概率分布函數求解的限制，需要對變量進行獨立性處理，難免出現信息失真，具有較大的局限性。為此，文獻[8]通過Copula函數直接對條件概率曲線進行離散，克服了離散求和法需要進行變量獨立性轉換的問題，提出了改進的離散求和法。隨機模擬法利用隨機模擬技術建立設計斷面及各分區洪水過程線的模擬模型，用人工方法隨機生成足夠長的、能滿足設計需要的洪水資料系列，通過長系列洪水資料直接求出設計斷面受水庫調洪影響后的洪水頻率曲線及設計值。該法的精度主要取決于所建立的隨機模型是否合理，能否反映洪水的客觀規律[9]。

本文結合隨機模擬法思想，考慮上游水庫調洪控制時段洪量和區間洪峰間的相關性，利用Copula函數構造其聯合分布；通過水庫調洪函數將水庫入庫洪量轉換為最大下泄流量，隨機模擬得到兩分區洪峰流量；提出推求水庫下游洪水概率分布的Copula-Monte Carlo(Copula-MC)方法。以清江流域隔河巖水庫為例對所提方法進行驗證，并探討是否考慮分區洪水空間相關性對計算結果的影響。

1 問題的數學描述

典型單庫防洪系統中A為上游水庫，C為設計斷面，B為水庫與設計斷面之間的區間流域。X、Y及QA分別為水庫A來水、區間B來水和經水庫A調蓄后的下泄洪水，顯然它們均可被視為隨機變量，概率分布函數分別用FX(x)、FY(y)及FQA(qA)表示。由于對調洪能力較大的水庫洪量往往其控制作用，因此令X表示洪量，Y與QA表示流量。QA由水庫來水X和水庫調洪函數gA(·)所確定(見圖1)

QA=gA(X)

(1)

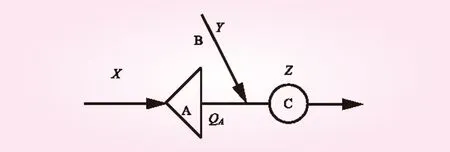
圖1 單庫防洪系統示意

斷面C處受水庫調洪影響后的洪水流量Z也是一隨機變量，并且等于水庫的下泄洪水QA與區間來水Y之和(考慮洪水傳播時間)，即

Z=QA+Y

(2)

現欲推求Z的概率分布FZ(z)。它可由QA和Y的聯合分布來確定，即聯合概率密度fQA,Y(qA,y)通過以下積分確定[2]。即

(3)

式中，qA0、y0分別為QA和Y的樣本空間的下界。

式(3)從理論上給出了FZ(z)的計算方法，但實際中往往因水庫最大下泄流量QA的概率分布非常復雜，常需分段處理；且QA、Y的空間相關性使得QA和Y的聯合分布難以求解。因此，本文擬采用Copula-MC法避開QA和Y聯合分布求解的難題，首先構造X和Y的聯合分布，再聯合抽樣模擬大量樣本(x，y)，通過水庫調洪函數qA=gA(x)得到(qA，y)，qA與y相加后統計得到設計斷面洪峰的概率分布曲線及設計值。

2 水庫調洪函數

在推求設計斷面洪水概率分布函數時，通常認為水庫本身的泄洪設施及調洪規則已經確定，假定水庫的泄量僅與來水有關[2]。對于調洪庫容較大的水庫，調洪結果主要受入庫洪水總量控制。假定來水x出現大小不同的洪量w1、w2…，選擇一個典型洪水過程線，按洪量控制放大過程線，并經水庫調洪演算，得到對應于wi的最大下泄流量qAi，點繪wi-qAi相關圖。如果水庫采用自由泄流方式，可根據點群中心采用一個曲線函數進行擬合求得該函數表達式qA=gA(x)。如果水庫有控泄要求，在某些洪量范圍內，下泄量qA成一水平直線，有時在某一洪量上下，下泄量發生突變。此時，可將洪量進行分段，對每一段采用不同的函數表達式擬合，將函數表達式組成函數組作為水庫的調洪函數一般可表示為[2，10]

(4)

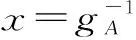
(5)

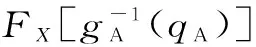
3 Copula-Monte Carlo方法

3.1 Copula函數

Copula函數是定義域為[0，1]均勻分布的多維聯合分布函數，根據Sklar定理，它可以將多個隨機變量的邊緣分布連接起來構造聯合分布。一般而言，水庫斷面和區間流域洪水之間存在較強的正相關性，通常采用Gumbel-Hougaard Copula函數來構造二者的聯合分布[11- 13]，數學表達式為

(6)

式中，u=FX(x)和v=FY(y)分別代表邊緣分布函數，Copula函數參數θ與Kendall秩相關系數τ的關系為θ=1/(1-τ)[14]。

3.2 推求水庫下游洪水概率分布的基本步驟

通過聯合分布函數可以對存在相關性的隨機變量X和Y成對地進行隨機抽樣，從而達到對二者同時隨機模擬的目的，進而給出計算水庫下游洪水概率分布的Copula-MC法。具體步驟如下[15]：

(1)根據建立的兩變量聯合分布，可以得到當X為指定值x時Y的條件分布，數學表達式為

(7)

(2)產生服從[0，1]均勻分布的兩個獨立隨機數r1和r2。

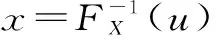
(4)令r2等于X=x時Y的條件分布值，即r2=SX(y|X=x)，式(7)計算繁瑣，為求解方便，將式(7)表達為

(8)

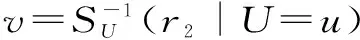
(5)通過z=qA+y計算得到z。

(6)重復步驟 2～5共n次，可以模擬出n個z值，采用數學期望公式[1]計算經驗頻率，得到水庫下游設計斷面的洪水概率分布。

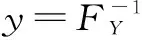
4 應用實例

清江是湖北省境內最大的一條長江支流，發源于湖北省利川市齊岳山，流域面積1.7萬km2(見圖1)，實例中A為隔河巖水庫，C為高壩洲斷面，B為隔河巖-高壩洲區間流域(簡稱“隔-高區間”)。隔河巖水庫控制面積14 430 km2，具有年調節能力；高壩洲水庫位于隔河巖水庫下游50 km處，控制面積15 650 km2，為徑流式電站，無調節能力；隔-高區間面1 220 km2，在此區間洪水傳播時間較短，可不考慮河道調蓄作用。隔河巖水庫為長江錯峰預留5.0億m3防洪庫容，必然會改變高壩洲斷面天然洪水的概率分布。

4.1 邊緣分布

按照我國《水利水電工程設計洪水計算規范》[1]的規定，假設隔河巖水庫斷面最大3 d洪量和隔-高區間、高壩洲斷面天然洪峰流量均服從P-Ⅲ分布，各水庫斷面和區間的天然設計洪水統計參數見表1。采用χ2檢驗法進行假設檢驗，在5%的顯著性水平下，自由度為k-r-1(r為參數個數，k為χ2檢驗的分組數)的χ2檢驗的接受域為小于等于臨界值，表中χ0.05為臨界值，3個隨機變量的P-III型分布均通過了檢驗。

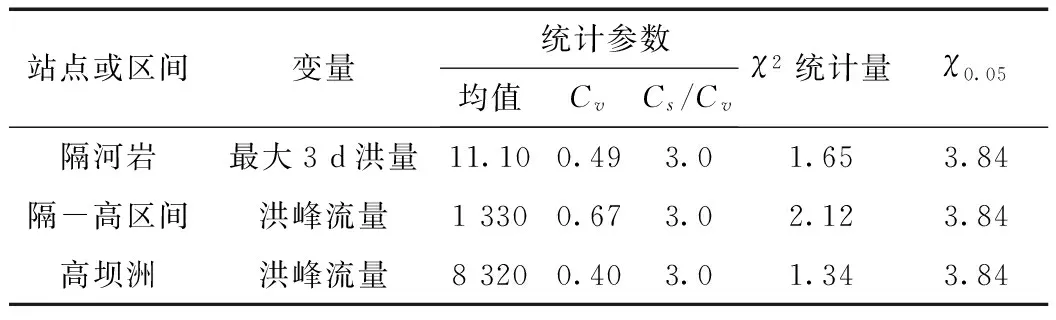
表1 各分區天然設計洪水統計參數

4.2 隔河巖水庫調洪函數

根據隔河巖水庫對洪水的調節特性，選取3d為控制時段。經計算，隔河巖斷面最大3d洪量2年一遇的值為9.82億m3，1 000年一遇的值為39.35億m3。在推求水庫調洪函數時，假定入庫洪量取值從8億～42億m3，離散間距0.05億m3，以離散的3 d洪量為控制，按1997年典型洪水過程線同倍比放大得到各自的設計洪水過程線，輸入到隔河巖水庫按調洪規則[9]進行調洪演算得到該洪量對應的最大下泄流量，點繪曲線(x，qA)(見圖2)。

某橋梁位于太原市某主干路上，為1座南北走向的5跨簡支普通鋼筋混凝土實心板梁橋，跨徑組合為5×6.7 m，橋梁中心線與河道中心線法線逆交10°，橋面總寬35 m。每跨上部結構均由33榀普通鋼筋混凝土實心板梁組成，人行道下實心板梁與車行道下實心板梁間無鉸縫連接，梁高均為0.33 m，每跨8號、9號、22號、23號實心板梁底寬均為1.5 m，其余板梁底寬均為1.0 m，橋面鋪裝為約20 cm厚的瀝青混凝土。該橋曾進行拓寬改建，改建時僅保留了老橋的下部結構，并于其兩側各新建了一幅橋。該橋梁的橫斷面示意圖見圖1。

對調洪函數進行分段擬合，得

(9)

圖2 隔河巖水庫調洪函數

對式(9)所得函數進行檢驗，將所有離散點據對應的洪量采用調洪函數進行計算得到對應的最大下泄流量，與實際調度值進行比較，發現相對誤差均不超過2%，表明簡化得到的調洪函數精度較高，能滿足計算要求。可由式(9)及隔河巖水庫天然來水最大3 d洪量的概率分布求得隔河巖水庫最大下泄流量的概率分布，如式(10)和圖3所示。

(10)

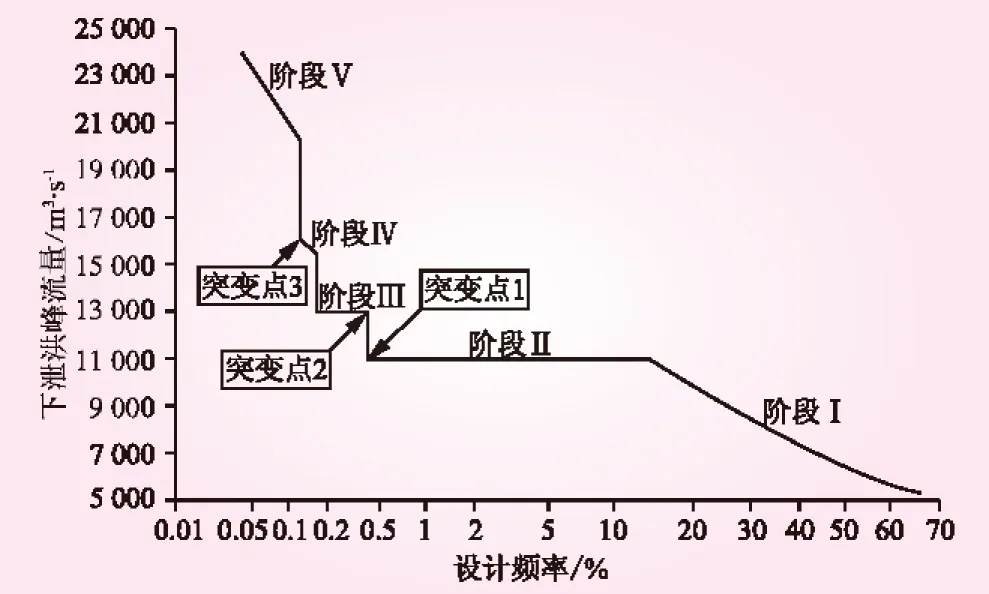
圖3 隔河巖水庫下泄洪峰的概率分布曲線

可以看出，根據入庫洪水量級的大小，可以將隔河巖水庫下泄洪峰的概率分布分為5個階段： I當入庫洪量<16.70億m3時，水庫按來多少水泄多少水的方式運行；II當入庫洪量>16.70億m3時，為滿足下游防洪要求水庫按一級控泄流量11 000 m3/s進行控泄；III當入庫洪量>33.15億m3時，為滿足下游防洪要求水庫按二級控泄流量13 000 m3/s進行控泄；IV當入庫洪量>37.09億m3時，表明該次洪水的量級已超過下游防洪標準，水庫不再承擔下游防洪任務，水庫敞泄運行；V當入庫洪量>38.35億m3時，表明該次洪水的量級已超過設計標準，同時臨時性啟用非常泄洪措施進行敞泄，以確保水庫的安全。階段I隨著入庫洪水量級的增大而逐步轉換到階段V。4次轉換過程中，只有階段I到階段II的轉換過程是漸變形成的，其他3次均為突變。3個突變點的設計頻率分別為0.41%、0.17%和0.125%。這造成最大下泄流量在區間(11 000， 13 000)、(13 000， 15 495) 、(16 038， 20 715) m3/s出現“空缺”。另外，在階段II和階段III由于水庫采用控泄的調洪方式，設計頻率[0.41%， 13.98%]對應的最大下泄流量均為11 000 m3/s；設計頻率[0.17%， 0.41%]對應的最大下泄流量均為13 000 m3/s。

“自下而上”類方法通常將下游設計斷面設計洪量分配給上游各分區以研究水庫的調洪影響。這類方法對洪量的分配方案具有很強的依賴性，科學合理的分配規則極為重要，當上游水庫具有復雜調洪規則(如有控泄要求)時，這類方法的可靠性較差，科學合理性將受到質疑[16]。本文所提Copula-MC法則不需要研究如何分配高壩洲斷面的設計洪量，可以考慮隔河巖斷面和隔-高區間洪水所有可能的組合遭遇情況，較好地反映洪水地區組成的隨機特性和水庫的調洪影響。

4.3 兩分區洪峰流量隨機生成

采用1958年～2010年隔河巖斷面最大3 d洪量和區間洪峰資料，得到秩相關系數為0.674，聯合分布的參數為3.07。通過聯合分布的經驗頻率和理論頻率，計算了實測樣本的均方根誤差(RMSE)[17]，結果為0.030 7，說明Gumbel-Hougaard Copula函數對聯合分布的擬合效果較好。將53年的經驗聯合分布值與理論聯合分布值點繪為圖4，其確定性系數為0.991 9，經驗頻率與理論頻率值的擬合情況很好。圖5是另外一種形式對聯合觀測變量的經驗聯合分布值與理論聯合分布值進行的對比。圖4和圖5表明所建立的聯合分布是合理可行的。

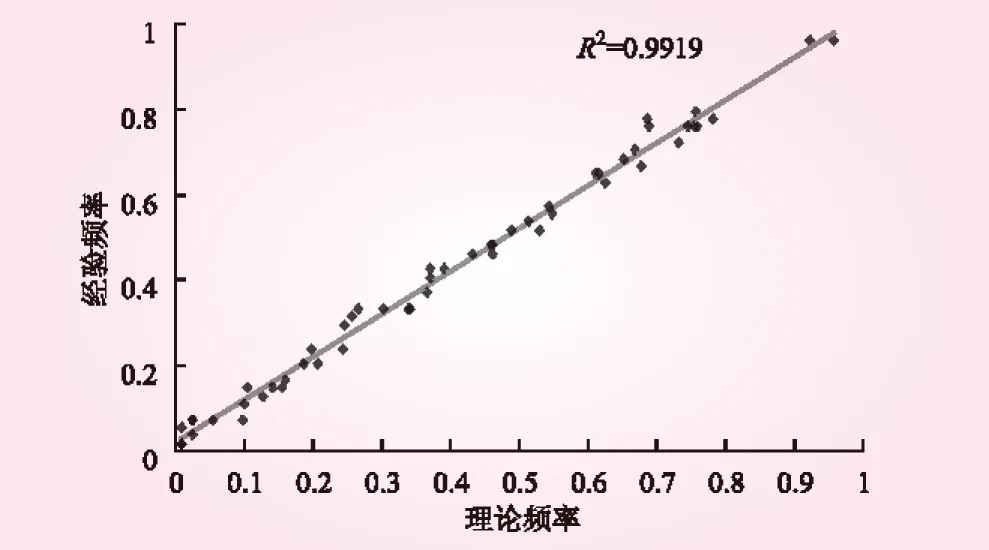
圖4 經驗頻率和理論頻率相關關系

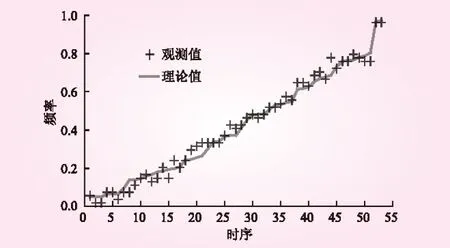
圖5 經驗頻率和理論頻率比較

運用上述3.2節中的Copula-MC法和獨立MC法，各模擬1萬組隔河巖水庫最大3d洪量及隔-高區間洪峰，結果點繪于圖6。對比圖6a和圖6b可知，考慮兩分區洪水的相關性情況下，隨機模擬的散點分布較為集中且散點在某一直線附近聚集，而未考慮時，散點均勻的散布在整個二維空間區域。這說明兩種方法模擬的隔河巖水庫最大3d洪量及隔-高區間洪峰組合差異較大。將實測資料點據點繪在隨機模擬的散點圖中，可以看出Copula-MC法由于考慮了洪水相關性，對實測資料的吻合效果更好，構建的隨機模型更能反映實際情況。

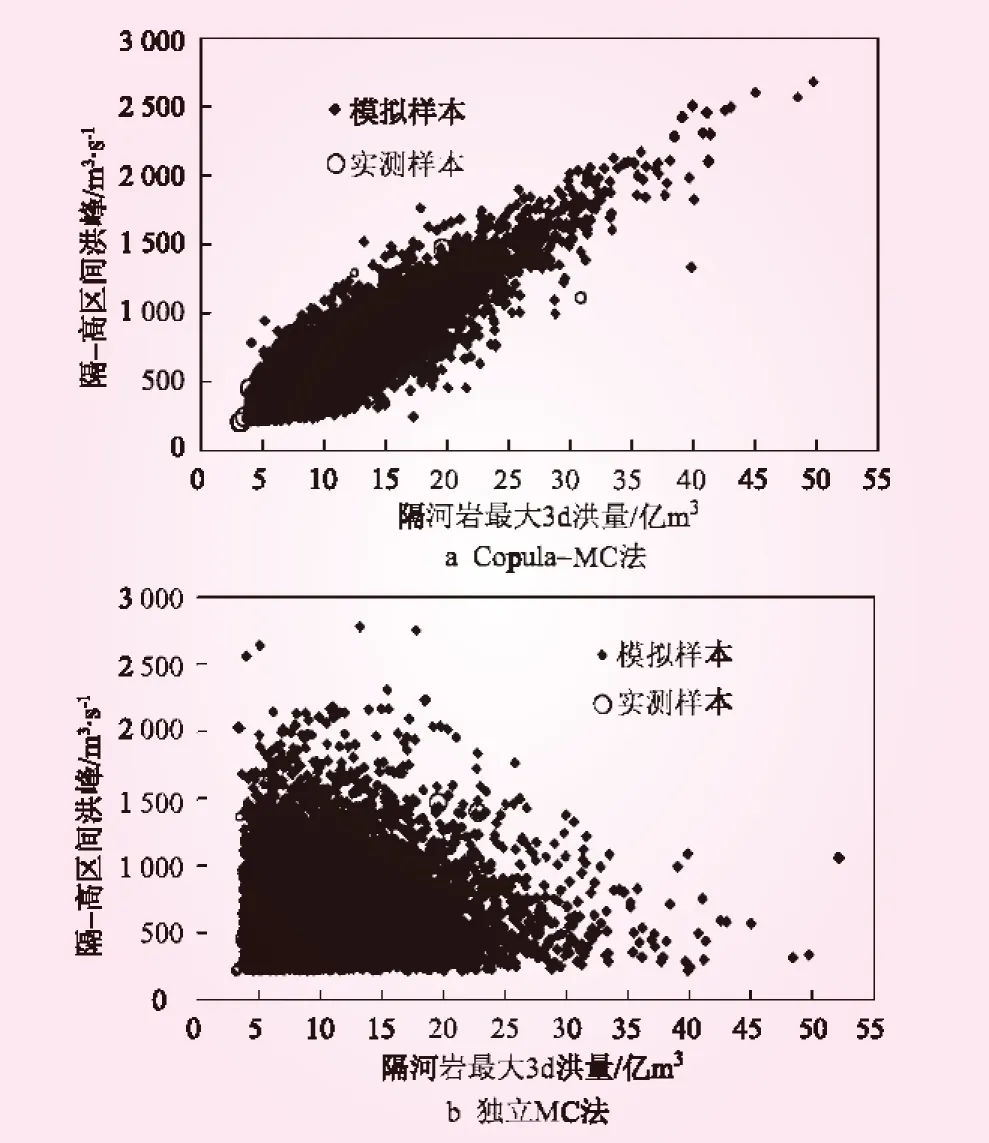
圖6 隔河巖斷面最大3 d洪量與隔-高區間洪峰隨機生成散點

4.4 受隔河巖水庫影響的高壩洲斷面洪水概率分布

利用上述隨機生成的大量高壩洲斷面洪峰流量，采用數學期望公式計算經驗頻率，得到Copula-MC法和獨立MC法計算得到的受隔河巖水庫影響的高壩洲斷面洪峰流量頻率曲線(見圖7)；同時，將天然情況下的高壩洲斷面洪峰流量頻率曲線也列于圖7，以便分析隔河巖水庫的調洪作用對高壩洲斷面洪峰流量頻率曲線的影響。將6種常用設計頻率的計算結果列于表2。

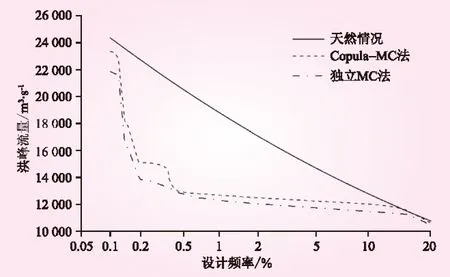
圖7 三種情形下高壩洲斷面洪峰流量頻率曲線

從圖7和表2的計算結果可以發現：與高壩洲斷面天然洪峰流量相比，兩種方法計算的受隔河巖水庫調蓄影響的洪峰流量均有不同程度的削減。可以發現，隔河巖水庫對于中小洪水的調節作用不顯著，故受其調洪影響的高壩洲斷面洪峰流量頻率曲線與天然情況無明顯差異；對于大洪水過程則調節能力逐漸減弱，整體規律與實際情況相符。與Copula-MC法相比，獨立MC法推求的高壩洲斷面洪峰流量系統偏小，最大可達10%左右。因此，不考慮兩分區洪水的空間相關性會低估高壩洲斷面的防洪風險。Copula-MC法計算的高壩洲斷面100年一遇洪峰流量由天然情況的18 800 m3/s減小為12 670 m3/s(此值相當于高壩洲斷面天然情況下10年一遇設計洪水)，削減6 130 m3/s(32.6%)。由此可知，隔河巖水庫的調洪作用對高壩洲斷面設計洪水的影響巨大。

表2 高壩洲斷面設計洪峰流量計算結果對比

5 結 論

應用清江流域隔河巖水庫實例對本文提出的方法進行驗證，主要研究結論如下：

(1)所提方法能充分考慮上游水庫斷面和區間洪水的空間相關性及地區組成的隨機性，結果合理可行。受隔河巖水庫調洪的影響，高壩洲斷面天然洪峰流量均有不同程度的削減，Copula-Monte Carlo方法推求的100年一遇設計洪水的削峰率達到32.6%。

(2)獨立Monte Carlo法假定各分區洪水相互獨立，忽略了洪水的空間相關性，計算的洪峰流量與Copula-Monte Carlo法相比系統偏小，會低估設計斷面的防洪風險。

[1] SL44—2006 水利水電工程設計洪水計算規范[S].

[2] 水利部長江水利委員會水文局， 水利部南京水文水資源研究所. 水利水電工程設計洪水計算手冊[M]. 北京： 中國水利水電出版社， 2001．

[3]謝小平， 黃靈芝， 席秋義， 等. 基于JC法的設計洪水地區組成研究[J]. 水力發電學報， 2006， 25(6)： 125- 129．

[4]黃靈芝， 謝小平， 黃強， 等. 梯級水庫設計洪水地區組成研究中的JC法[J]. 自然災害學報， 2006， 15(4)： 163- 167．

[5]閆寶偉， 郭生練， 郭靖， 等. 基于Copula函數的設計洪水地區組成研究[J]. 水力發電學報， 2010， 29(6)： 60- 65．

[6]劉章君， 郭生練， 李天元， 等. 基于Copula函數的梯級水庫設計洪水地區組成研究[J]. 水資源研究， 2014， 3(2)： 124- 135．

[7]劉章君， 郭生練， 李天元， 等. 梯級水庫設計洪水最可能地區組成法計算通式[J]. 水科學進展， 2014， 25(4)： 549- 558．

[8]李天元， 郭生練， 劉章君， 等. 梯級水庫下游設計洪水計算方法研究[J]. 水利學報， 2014， 45(6)： 641- 648．

[9]李雨， 郭生練， 周研來， 等. 考慮入庫洪水隨機過程的梯級水庫防洪優化調度[J]. 四川大學學報： 工程科學版， 2012， 44(6)： 13- 20．

[10]何長寬. 用概率組合法確定并聯水庫下游洪峰流量的概率分布[J]. 水利水電技術， 1998， 29(7)： 49- 51．

[11]張娜， 郭生練， 肖義， 等. 基于聯合分布的設計暴雨方法[J]. 水力發電， 2008， 34(1)： 18- 21．

[12]楊立峰， 周研來， 夏世明， 等. 基于阿基米德聯合函數的洪水過程隨機模擬研究[J]. 水力發電， 2011， 37(4)： 20- 23．

[13]馮平， 李新. 基于 Copula 函數的非一致性洪水峰量聯合分析[J]. 水利學報， 2013， 44(10)： 1137- 1147．

[14]劉和昌， 梁忠民， 姚軼， 等. 基于 Copula 函數的水文變量條件組合分析[J]. 水力發電， 2014， 40(5)： 13- 16．

[15]肖義， 郭生練， 熊立華， 等. 一種新的洪水過程隨機模擬方法研究[J]. 四川大學學報： 工程科學版， 2007， 39(2)： 55- 60．

[16]王銳琛， 陳源澤， 孫漢賢. 梯級水庫下游洪水概率分布的計算方法[J]. 水文， 1990， 9(1)： 1- 8．

[17]郭生練， 閆寶偉， 肖義， 等. Copula函數在多變量水文分析計算中的應用及研究進展[J]. 水文， 2008， 28(3)： 1- 7．

(責任編輯 陳 萍)

Flood Probability Distribution Estimation under the Influence of Upstream Reservoir Regulation Based on Monte Carlo Method

LIU Zhangjun， GUO Shenglian， HU Yao， YANG Guang， YING Jiabo

(State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University， Wuhan 430072， Hubei， China)

The joint distribution of controlling flood volume at reservoir site and peak discharge at interval basin is firstly constructed based on Copula function， then the reservoir inflowing flood volume is transformed into outflow peak discharge by using flood regulation function and the flood peak discharge at the two sub-basins is got by using stochastic simulation method， and finally the Copula-Monte Carlo (Copula-MC) method for flood probability distribution estimation is developed. The Qingjiang basin is chosen as the case study and the peak discharge probability distribution of Gaobazhou site is estimated under the influence of Geheyan Reservoir by using Copula-MC method， and the results are compared with Independence-MC method that ignores the correlation. The results demonstrate that the flood peaks of Independence-MC method are systematically smaller than those of Copula-MC method， which may lead to an increased risk in Gaobazhou site， and the 100-year design peak discharge estimated by Copula-MC method at Gaobazhou site has been cut by 32.6%. The calculation results of proposed Copula-MC method are reasonable because it can capture the spatial correlation of floods occurred at each sub-basin and reflects the stochastic characteristics of flood region composition．

reservoir regulation; probability distribution; Copula function; Copula-Monte Carlo method; Qingjiang Basin

2014- 12- 12

國家自然科學基金重大項目(51190094)

劉章君(1991—)，男，江西吉安人，博士研究生，研究方向為水文分析與計算.

TV122.3

A

0559- 9342(2015)08- 0017- 06