碎紙片拼接復原的算法研究

郭 偉，崔艷星

（長治學院 數學系,山西 長治 046011）

1 引言

破碎文件的拼接在司法物證復原、歷史文獻修復以及軍事情報獲取等領域都有著重要的應用。傳統上,拼接復原工作需由人工完成，準確性較高,但效率較低。當碎片數量巨大，人工拼接很難在短時間內完成任務。隨著計算機技術的發展，人們試圖開發研究碎紙片的自動拼接技術，以提高拼接復原效率。現對以下問題進行討論：對給定的來自同一頁印刷文字文件的碎紙機破碎紙片（僅縱切）,建立碎紙片拼接復原模型和算法,并對附件1給出的一頁文件的碎片數據進行拼接復原。復原結果表達以圖片形式表達。

2 復原算法思想描述

對于給定的來自同一頁印刷文字文件的碎紙機破碎紙片（僅縱切）；首先，通過觀察這些字的特點,可以通過人工干預[1]將紙條左邊全是整字、符號的碎紙條找出來,這就找出了這些紙條中的第一條。同樣，我們可以確定出最后一條碎片。因為每條碎紙片中離邊緣最近的那些字，有的是整字，有的是半字,有的是符號,有的是空格,所以對碎片的拼接有一定的難度.為了使問題簡單化,我們聯想到把文字轉化為數字,其中這些數字用“0”或者“1”來代替；半個字用0表示,整個字、符號、空格都用1表示。

其次,我們把紙條中最左邊轉化成的數字按所在行形成左向量,同樣最右邊的那些文字形成一個右向量。這樣每個碎紙條都可以用兩個向量來表示。進而我們就把碎紙片文字的拼接問題轉化為向量是否相等的問題了。如果一個紙條的左向量和另一個紙條的右向量相等,說明這兩條紙條可拼接到一起，這個過程可利用c#編程完成排序[2]。

最后,根據上述排序結果,利用MATLAB程序可以檢驗c#編程運行結果并實現紙片的復原[3,4]。

3 復原算法的實現

首先,從對于給定的來自同一頁印刷文字文件的碎紙機破碎紙片（僅縱切）的向量中找出初始向量。因為破碎前紙片的最左邊的字都是整字,我們可以通過人工干預,很容易把都是整字的碎紙條找出來,即左向量是[0,0,…,0,0]的紙條找出來。這樣我們就找出了初始向量。假如找到的初始向量為Li,則初始向量所在紙條的右向量為。

其次，尋找與Ri相等的向量Lj（其中i 不等于j）。假如Ri-Lj=0,即Ri與Lj相等,則第i-1條碎片與第j-1條碎片拼接成功.成功后再用Rj尋找下一條。假如Rj-Lk≠0,則說明Rj與Lk不相等,則第j-1條碎片與第k-1條碎片拼接不成功,不成功的話再用Rj-Lk是否等于0來尋找下一條,{其中,k≠j}；假如Ri-Lj≠0則假如有Ri-Lh=0,則拼接成功.假如Ri-Lh≠0,則依次類推。

最后,由Rm-Ln=0.則碎紙片排序完成。對于上述過程。我們建立了如下的流程圖：

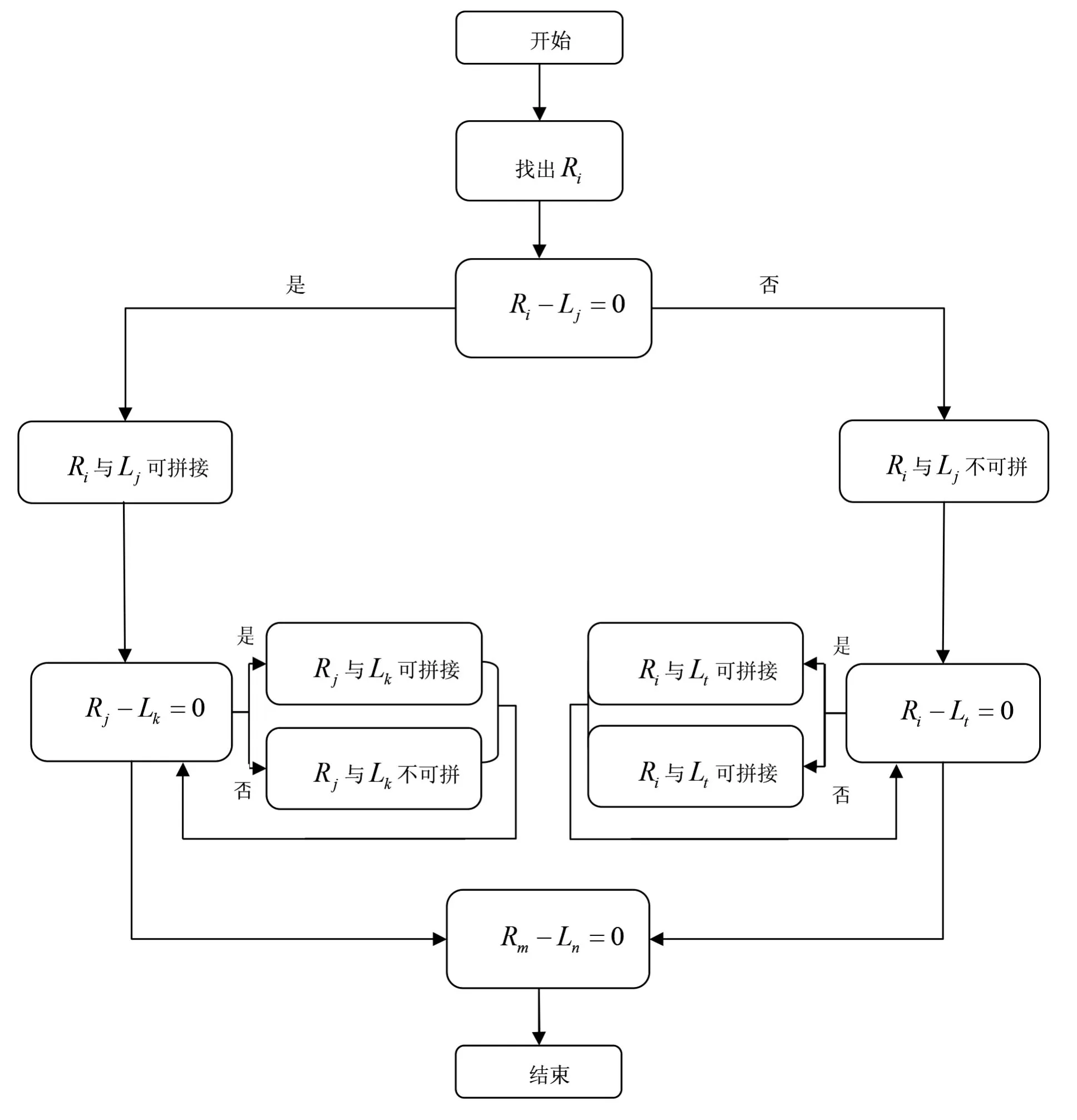
例如：下圖是給定碎片，共19支(從左至右編號000～018)，現將其復原。

首先，找到其中左側為整字的碎片，向量表示結果見附錄1,上圖中第一條碎片是第8條碎片,最后一條碎片是第6條碎片,所以在用該流程時,i=9,n=7。然后,利用MATLAB程序,檢驗結果并將碎紙片拼接復原。具體程序見附錄2.復原圖片結果分別見附錄3。

4 附錄

附錄1

L1=[1,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1]

R1=[0,0,0,0,0,0,1,1,0,0,0,0,1,0,0,1,0,1,1,0,0,0,0,0,0,0,0,1]

L2=[1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,1,0,0,0,0,0,0,0,1,0,0]

R2=[0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0]

L3=[0,0,0,0,0,0,1,1,0,0,1,0,1,1,0,0,1,0,1,0,0,0,1,0,1,0,0,1]

R3=[0,1,0,0,0,0,0,0,1,1,0,1,0,1,0,1,0,1,0,0,0,1,0,1,0,0,0,0]

L4=[0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0]

R4=[0,0,0,1,0,0,0,1,1,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0]

L5=[0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0]

R5=[0,0,0,0,1,1,0,1,0,1,0,0,0,1,0,1,0,1,1,1,1,0,0,0,0,0,0,0]

L6=[0,0,0,0,1,1,0,1,0,1,0,0,0,1,0,1,0,1,1,1,1,0,0,0,0,0,0,0]

R6=[0,0,0,1,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,1,0,1,1,0,0]

L7=[0,0,0,0,0,0,1,1,0,0,0,0,1,0,0,1,0,1,1,0,0,0,0,0,0,0,0,1]

R7=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]

L8=[1,1,0,1,0,0,1,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,0,0]

R8=[0,0,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,1,0,0,1,0,0,0,0,0,0,1]

L9=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]

R9=[1,0,1,0,1,1,0,1,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0]

L10=[0,0,0,1,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,1,0,1,1,0,0]

R10=[0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0]

L11=[0,0,0,1,0,0,0,1,1,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0]

R11=[0,0,0,0,0,0,1,1,0,0,1,0,1,1,0,0,1,0,1,0,0,0,1,0,1,0,0,1]

L12=[0,0,1,1,1,1,1,0,1,1,0,0,0,0,1,1,1,1,0,0,0,0,0,1,0,0,1,0]

R12=[1,1,0,1,0,0,1,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,0,0]

L13=[1,0,0,1,0,0,0,1,0,1,0,1,1,1,0,1,1,1,1,1,1,1,1,0,1,0,0,1]

R13=[0,0,1,0,1,1,1,0,1,0,1,1,0,1,1,0,0,1,0,1,1,1,0,1,1,1,1,1]

L14=[0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0]

R14=[1,0,1,0,1,1,1,0,0,0,0,0,1,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0]

L15=[1,0,1,0,1,1,0,1,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0]

R15=[1,0,0,1,0,0,0,1,0,1,0,1,1,1,0,1,1,1,1,1,1,1,1,0,1,0,0,1]

L16=[0,0,1,0,1,1,1,0,1,0,1,1,0,1,1,0,0,1,0,1,1,1,0,1,1,1,1,1]

R16=[0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0]

L17=[0,1,0,0,0,0,0,0,1,1,0,1,0,1,0,1,0,1,0,0,0,1,0,1,0,0,0,0]

R17=[1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,1,0,0,0,0,0,0,0,1,0,0]

L18=[0,0,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,1,0,0,1,0,0,0,0,0,0,1]

R18=[1,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1]

L19=[1,0,1,0,1,1,1,0,0,0,0,0,1,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0]

R19=[0,0,1,1,1,1,1,0,1,1,0,0,0,0,1,1,1,1,0,0,0,0,0,1,0,0,1,0]

附錄2

I1=imread ('008.bmp');

I2=imread ('014.bmp');

I3=imread ('012.bmp');

I4=imread ('015.bmp');

I5=imread ('003.bmp');

I6=imread ('010.bmp');

I7=imread ('002.bmp');

I8=imread ('016.bmp');

I9=imread ('001.bmp');

I10=imread ('004.bmp');

I11=imread ('005.bmp');

I12=imread ('009.bmp');

I13=imread ('013.bmp');

I14=imread ('018.bmp');

I15=imread ('011.bmp');

I16=imread ('007.bmp');

I17=imread ('017.bmp');

I18=imread ('000.bmp');

I19=imread ('006.bmp');

I=[I1,I2,I3,I4,I5,I6,I7,I8,I9,I10,I11,I12,I13,I14,I15,I16,I17,I18,I19];imshow（I）

附錄3

［1］韓中庚,數學建模方法及其應用,第二版［M］.北京：高等教育出版社,2009.

［2］王聚豐,楊啟帆.數學建模案例集［M］.北京:高等教育出版社,2003.

［3］司守奎,孫璽菁.數學建模算法與應用［M］.北京：國防工業出版社,2011.

［4］賈海燕,碎紙自動拼接,http://www.docin.com,2013年9月15日［DB/OL］.