三角輪系式移動機構動力學建模及仿真
岳龍旺,朱敬花,吳利濤,武可艷
(1.河南工業大學機電工程學院,河南鄭州 450007;2.天津世紀天源安全衛生監測有限公司,天津 300191)
0 前言
輪椅是下肢傷殘者和年老體弱者出門時必不可少的代步工具,但是傳統的輪椅不具備爬樓和越障功能。隨著機器人技術的發展,各種新型移動式機器人輪椅不斷涌現。對于新型輪椅來說,爬樓和越障能力是衡量其性能的重要指標。具備爬樓和越障功能的移動機器人多采用輪式、腿式、履帶式、復合式移動機構。履帶式移動機構體積大,比較笨重,能量效率低。在平地行駛過程中劣勢比較明顯,不能滿足快速移動的要求;腿足式移動機構結構復雜、控制難度大,目前仍處于實驗室研究階段;復合式移動機構結構復雜、控制難度大,有效載荷小;輪式移動機構機動性好、結構簡單、易于控制、能量消耗低,但其越野性能較差,通常只能越過高度小于車輪半徑的障礙物。為提高輪式移動機構的越障能力,國內外專家學者開發了多種輪式移動機構[2-5]。在輪式移動式機構中,三角輪系式移動機構因其既有輪式機構的輕便、靈活、高效,又能實現爬樓和越障功能而受到重視。三角輪系式移動機構的運動學、動力學特性對于保證移動式機器人的爬樓和越障性能、提高乘坐舒適性有重要影響[6-7]。
基于對三角輪系式機構分析與綜合,利用拉格朗日法建立了三角輪系的動力學模型,利用MATLAB的Simulation工具箱對其工作特性進行了仿真分析,得到三角輪系控制參數與爬樓機器人工作性能的映射關系,為三角輪系式爬樓越障機器人控制系統設計奠定了基礎。
1 三角輪系式移動機構
移動機構的三角輪系結構示意圖如圖1所示,其單側三維結構示意圖如圖2所示。在平整的路面上行駛時,三角輪系中的任意兩輪先著地,在運動的過程中約束系桿7不能轉動只能隨車輪做平移運動,此時的驅動輪系轉變為定軸輪系,此時小車在平整路面可以快速行駛,由于此時的兩個車輪都為驅動輪,有效利用了三角輪系的質量,也增加了車輪和地面的接觸面積,提高了爬樓越障機器人在松軟地面的通過能力。根據差動輪系的傳動比關系,當爬樓越障機器人遇到障礙物時,系桿7將帶動整個三角輪系繞中心軸6轉動,通過三角輪系的翻轉實現爬樓越障功能。
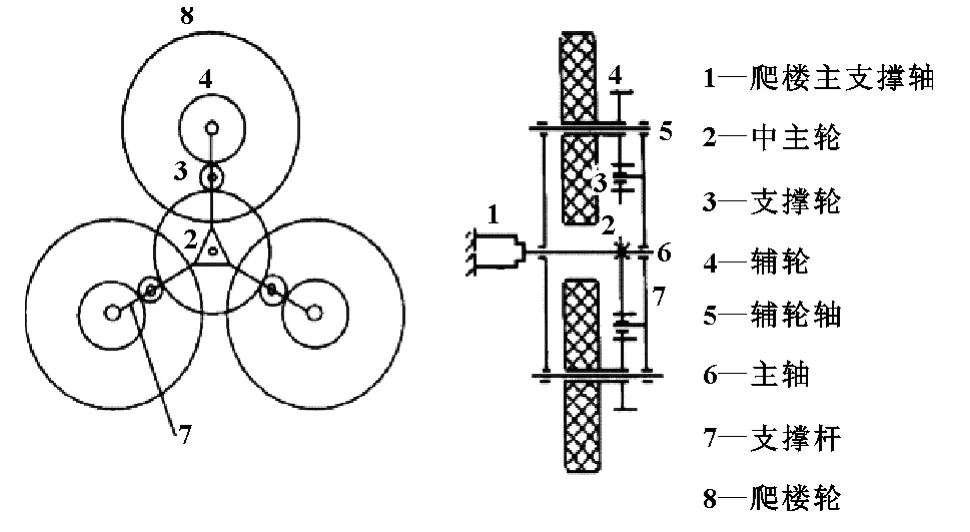
圖1 三角輪系結構示意圖

圖2 三角輪系單側三維結構示意圖
2 三角輪系拉格朗日動力學模型
為簡化計算,假定三角輪系與臺階間不會發生打滑現象。由于運動速度不高,所以可忽略運動系統因慣性力引起的動載荷。采用拉格朗日法對三角輪系進行動力學建模[8-9]。
2.1 三角輪系平移運動動力學模型
當三角輪系作平移運動時,只有各個輪子的自轉,沒有輪系的公轉。當爬樓越障機器人在斜面上做平動運動時,只有一個沿x軸的自由度,取χ為廣義坐標,其中θ為爬樓機器人的爬坡角度。以三角輪系的中心為研究對象來研究整個機器人的運動情況,如圖3所示。
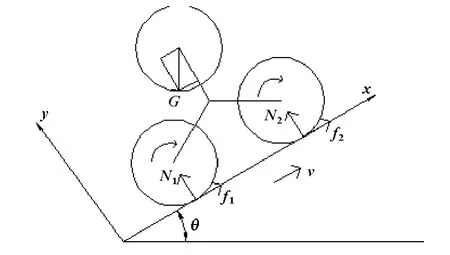
圖3 三角輪系平移運動示意圖
系統勢能Ep即三角輪系中心的高度變化所引起的勢能:
系統廣義力Qχ為:

其中M力矩為電機作用在三角輪系中兩個行走輪的力矩轉變成的摩擦力對三角輪系的驅動力,只有當f=時爬樓機器人才向前運轉。
應用拉格朗日方程:
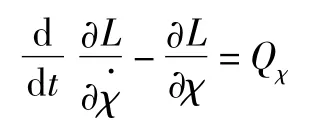
得爬樓機器人的動力學模型:
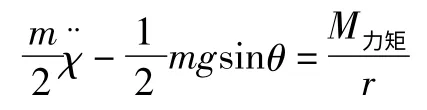
2.2 三角輪系翻轉運動動力學模型
當爬樓機器人在攀爬樓梯時兩個驅動電機停止工作,只有翻轉電機工作,即爬樓機器人在此過程中只發生翻轉運動,因此它只有一個翻轉自由度,假定其翻轉角度為θ,取θ為廣義坐標向量,如圖4所示。
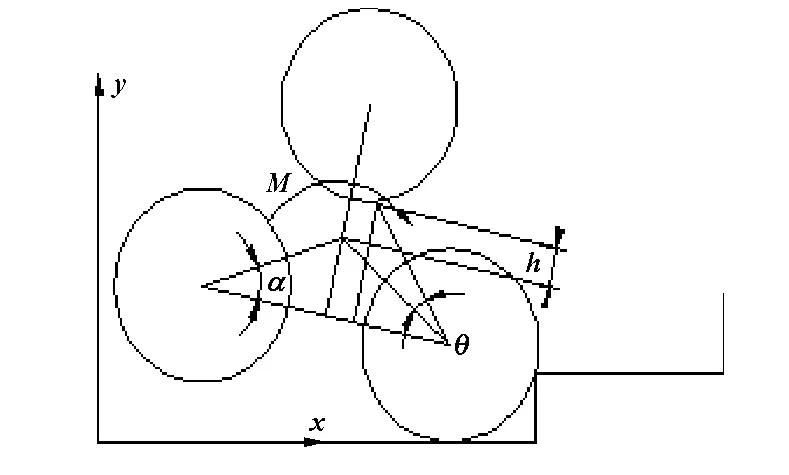
圖4 三角輪系爬樓時狀態示意圖
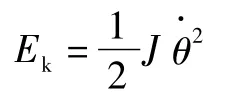
則系統動能Ek為:。系統勢能Ep為:
其中J為爬樓機器人的轉動慣量,
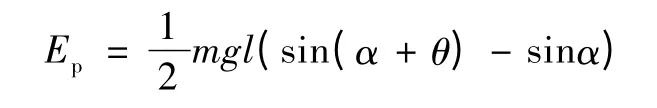
其中α=30。
則拉格朗日算子L為:
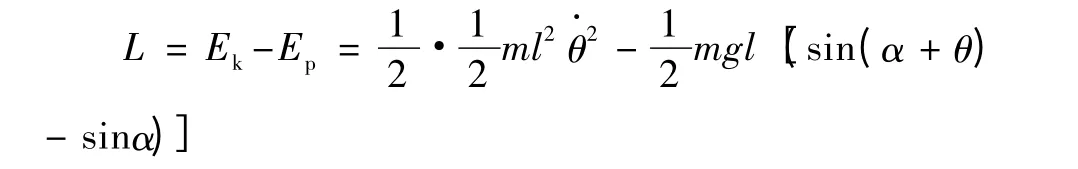
系統廣義力Qχ為:
Qθ=M翻轉力矩
應用拉格朗日方程:
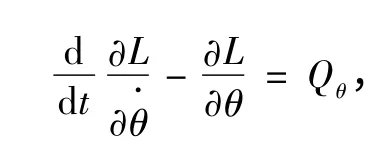
代入上式可得:
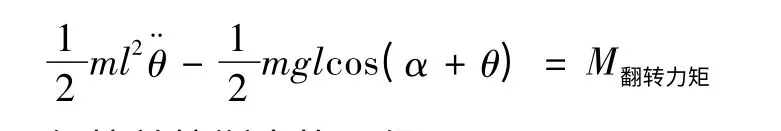
經拉普拉斯變換可得:
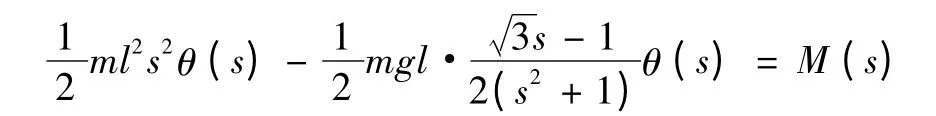
代入爬樓機器人的具體參數可得其實際模型的傳遞函數:
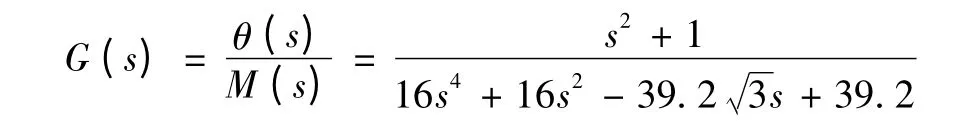
取重力加速g=9.8 m/s2。
3 仿真分析
利用MATALAB里面的Simulink(Dynamic System Simulation)工具箱進行仿真。MATLAB中的PID函數可以對爬樓機器人進行控制分析,利用Z-N法則來調整PID參數可以使其達到近似穩定,以實現三角輪系式移動機器人的穩定運行[8-10]。
3.1 PID控制分析
前面已經得到了爬樓機器人小車的開環傳遞函數,輸入為電機輸送給機器人小車的翻轉力矩Mfanzhuan,輸出為小車圍繞輪組中心旋轉的翻轉角度θ,被控對象實際模型的傳遞函數為:
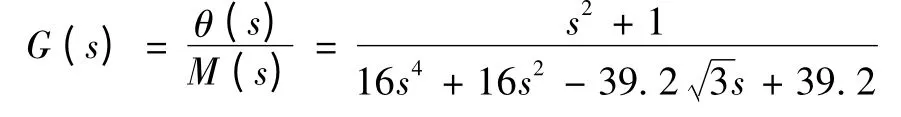
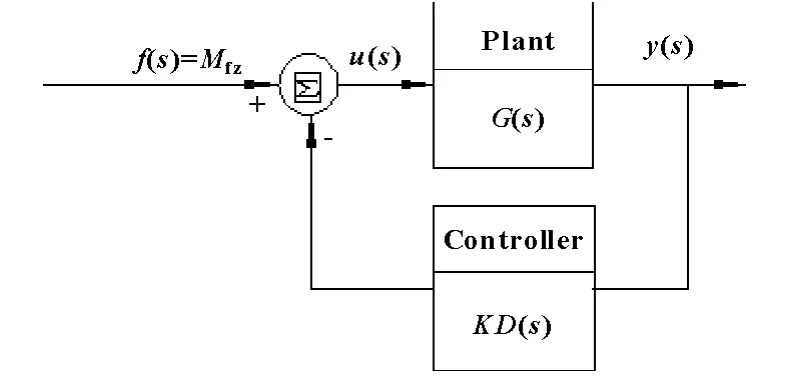
給系統施加一個脈沖擾動,輸出量為爬樓機器人的翻轉角度時,系統框圖如圖5所示。其中KD(s)是PID控制器的傳遞函數,G(s)是被控對象爬樓機器人小車的傳遞函數。
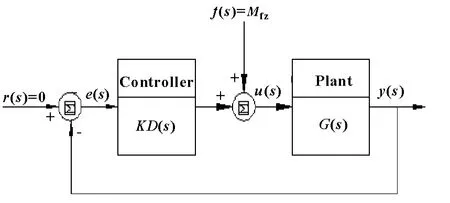
當輸入r(s)=0,爬樓機器人的結構框圖變成圖6所示的傳遞函數,該系統的輸出為:
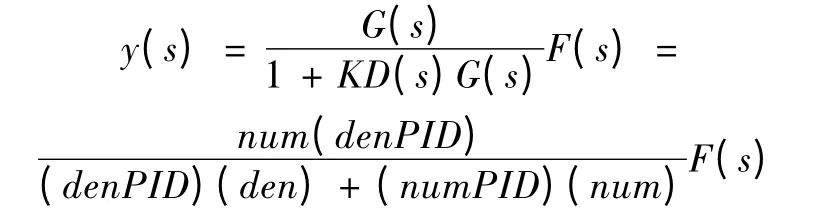
式中:num、den為爬樓機器人傳遞函數的分子項和分母項,numPⅠD、denPⅠD為控制器傳遞函數的分子項和分母項,K為PID控制器的增益。
3.2 PID控制器的參數整定
在MATLAB的Simulink工具箱中建立爬樓機器人攀爬樓梯時的模型如圖7所示,其中PID controller是封裝之后的PID控制器。
利用齊格勒-尼克爾斯第二法則簡稱Z-N法則進行PID控制器的參數整定,假設Ti=∞,Td=0,即只有比例控制kp,將比例系數kp由零逐漸增大到系統的輸出首次呈現持續的等幅振蕩,如圖8所示,此時對應的臨界增益kc=600,振蕩周期Tc=0.3 s,根據Z-N法則可知:kp=0.6kc,Ti=0.5 Tc,Td=0.125·Tc,則PID控制器參數為:kp=0.6kc=360,ki=kp/Ti=1 200,kd=kp·Td=108[11]。
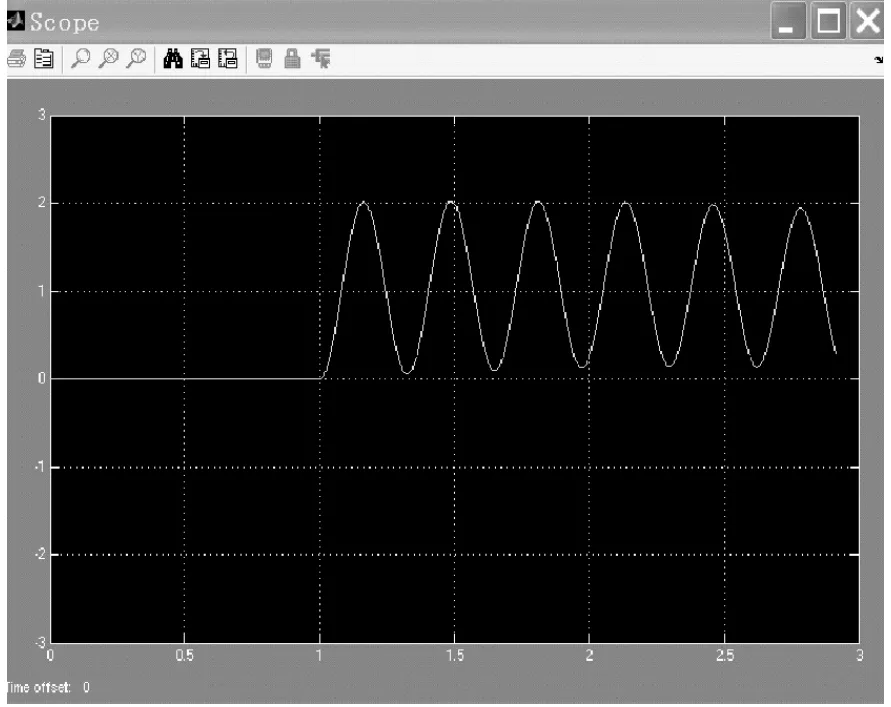
圖8 P控制仿真結果圖(kc=600)
3.3 仿真分析
將PID參數值kp=0.6kc=360,ki=kp/Ti=1 200,kd=kp·Td=108[11],代入仿真模型,得控制系統仿真結果如圖9所示。由仿真結果圖可以看出,系統在1.2 s左右的時間內可以達到穩定,超調量為20%,因此此系統有較好的穩定性。
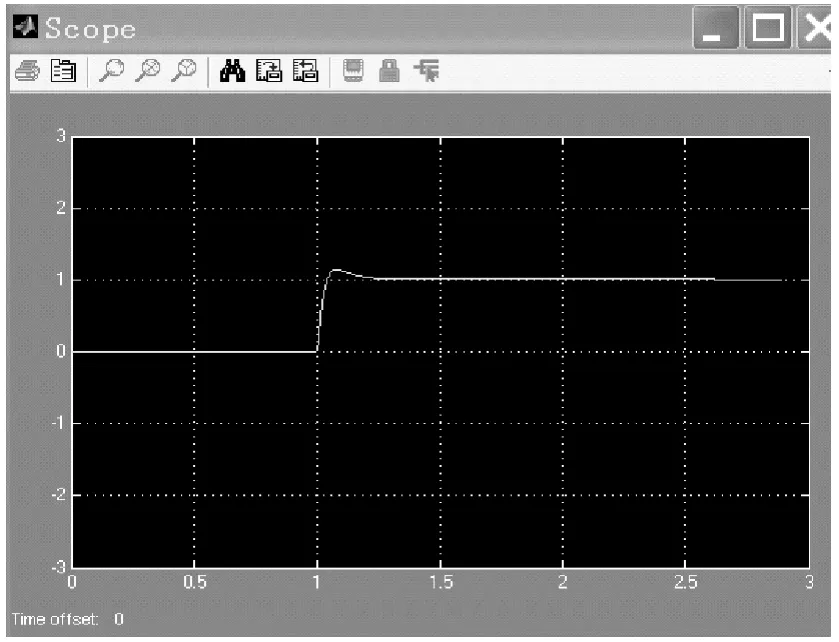
4 結束語
三角輪系式移動機構的動力學特性是影響爬樓越障機器人性能的重要因素。利用拉格朗日法對三角輪系進行動力學模型,利用MATLAB對控制系統進行仿真,分析結果對于爬樓越障機器人控制系統設計有重要參考價值。
[1]武明,馬希金.一種新型爬樓梯輪椅的動力學建模及穩定性分析[J].中國生物醫學工程學報,2000,19(3):47-50.
[2]NANDY G C,XU Y.Dynamic Model of a Gyroscopic Wheel[C].Robotics and Automation,1998.Proceedings.1998 IEEE International Conference on.IEEE,1998.
[3]HAYATI S,VOLPE R,et al.The Rocky 7 Rover:a Mars Science craft Prototype[C].Proceedings of IEEE International Conference on Robotics and Automation,1997.
[4]吉炎.懸臂式六輪移動機器人越障性能研究[D].長沙:中南大學,2006.
[5]BOT@4000 Mobility System,Independence Technology.L.L.C.http://www.ibotnow.com[OL].
[6]YUE Longwang,WU Keyan,LIU C B.Study of a New Stair-climbing and Obstacle-traversing Robot[J].Advanced Materials Research,2011,211:686-690.
[7]YUE Longwang,WU Keyan,TU W Q.Design and Analysis of Stair-Climbing and Obstacle-Traversing Robot[J].2011,224(2):224-225.
[8]固高科技有限公司.倒立擺實驗系統[M].2005.
[9]魯墨武,石磊.基于MATLAB的機器人建模與動力學仿真[J].制造業信息化2010,47(10):40-43.
[10]NALECZAndrze G.Influence of Vehicle and Roadway Factor on the Dynamics of Tripped Rollover[J].International Journal of Vehicle Ddsign,1989,10(3):321-346.
[11]鄒伯敏.自動控制理論[M].北京:機械工業出版社,2007.
- 機床與液壓的其它文章
- Manufacturing of self-lubricating diamond tools with Ni-Cr alloy adding with Ni/C
- Vibration response analysis of a lathe spindle by using the ANSYS finite element method
- Car following model with consideration of the vehicle’s mechanical inertia effect and its stability analysis
- Software design for spur gear tooth thickness based on MATLAB/GUI
- Dynamic study on ultrasonic horn
- Analysis and research of OPC technology in coal mine monitoring data transmission system

