數控機床進給系統精度保持性研究

王義強，胡斌峰，楊林霖

(1．浙江大學寧波理工學院，浙江寧波 315100;2．浙江大學機械與能源工程學院，浙江杭州 315000)

0 前言

隨著現代制造技術的飛速發展，數控機床作為最普遍、最重要的現代工作母機［1］，自20世紀50年代誕生以來［2］，以其強大的柔性制造能力得到了飛速發展與廣泛應用。然而，國產數控機床在精度保持性上一直落后于國外高端產品［3-4］，這也導致了國產數控機床國內市場占有率普遍偏低。精度保持性不僅體現在機床進給系統的定位精度，更重要的是機床在長時間工作中，持續保持原有定位精度和重復定位精度的能力。目前國家標準一直沒有對機床的精度保持性進行嚴格的定量規定，而實際操作中的各種原因也導致了對機床的精度保持性的評估一直是業內的一項難題。缺乏良好的精度保持性，數控機床的質量就沒有保證，其理論研究和生產實踐均受到制約［5］。因此，對國產數控機床進給系統的精度保持性進行試驗研究，分析其衰減變化模型，可以有效增強數控機床的可靠性。

1 精度保持性理論模型

1．1 精度保持性定義

1．1．1 精度失效事件

精度失效事件通常是指進給系統實際工作精度超出規定的工作精度范圍，這里的工作精度主要指系統的單向定位精度、雙向定位精度和重復定位精度。對于文中而言主要研究機械部件的磨損、疲勞等有害過程對機械傳動系統定位精度產生的影響，因此為了排除伺服系統、部件間隙對測量結果的影響，只對其單向定位精度進行可靠性分析及建模。因此文中精度失效事件指的是進給系統前后兩次測量得到的單向定位精度的變化量，超過了預先規定的最大變化值。

1．1．2 精度保持時間(距離)

精度保持時間(距離)，指的是相鄰兩次精度失效事件的間隔時間(距離)。這里的時間是廣義的，可以是系統連續工作的時間或累計移動的距離。

1．1．3 精度可靠度和精度失效概率

精度可靠度R(x)，指的是進給系統在考察行程x內不發生精度失效故障的概率。精度失效概率F(x)，指的是在考察行程x內產品發生精度故障的概率。產品在行程x的單位距離內發生失效的概率稱作失效概率密度函數f(x)。

1．2 非齊次泊松過程(NHPP)

在規定的條件與時間內，產品完成規定功能的能力稱為可靠性［6］。進給系統精度失效是在多種過程共同作用之下產生的結果［7］，例如導軌的振動、絲杠的磨損等，且這些過程通常都是隨機的。所以，精度失效事件的發生具有隨機性，并且服從一定的概率分布，因而可以參照可靠性統計模型進行數據分析。

文中的可靠性預測模型主要是考察隨著行程累積產品故障次數的變化規律。記N(x)(x＞0)為產品在(0，x］內的累積故障次數，非齊次泊松過程是指同時滿足以下3個條件的計數過程［8］:

(1)N(0)=0，且N(x)是累積行程x的非減函數;

(2){N(x)，x＞0}具有獨立增量，即在行程區間(0，s］與(s，x］內發生的故障次數N(s)與N(x)-N(s)是相對獨立的;

(3)在短時間段(x，x+h］內，發生一次故障的概率為:產品在行程區間(x，x+s］內累計故障次數為k的概率為:

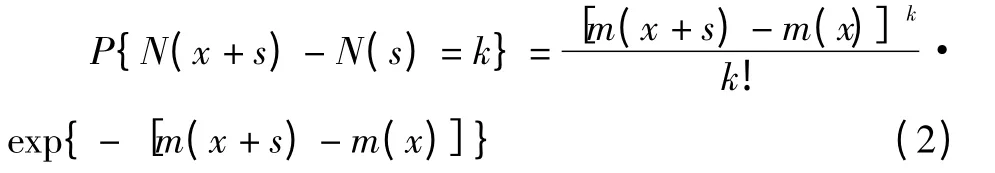
其中:λ(x)為失效率函數，是指單位行程內產品失效的次數;均值函數為，表示(0，x］內產品平均失效次數。

1．3 預測理論模型

AMSAA理論描述的冪律過程是非齊次泊松過程(NHPP)的一種［9-10］，其失效率函數和均值函數分別如下:

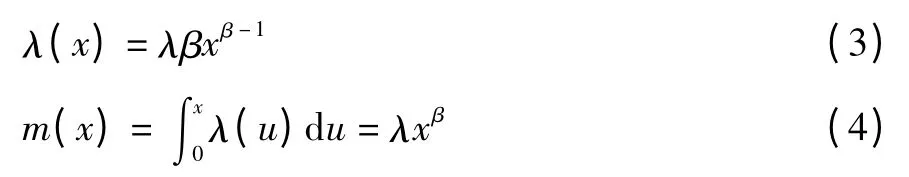
其中:λ＞0，β＞0。

設數組(x1，x2，…，xn)是計數過程N(x)觀測到的n次精度故障對應的累積行程Xi(i=1，2，…，n)的樣本值，且x1≤x2≤…≤xn。為了得到(X1，X2，…，Xn)的聯合密度函數，需對精度故障發生區間的概率進行分類。若(X1，X2，…，Xn)的聯合密度函數為f(x1，x2，…，xn)，則在n個小區間(x1，x1+d x1］，(x2，x2+d x2］，…，(xn，xn+d xn］上各發生一次精度故障的概率為:

令Ai(i=1，2，…，n)表示在區間(xi，xi+d xi］上發生1次精度故障的事件，Bi(i=1，2，…，n)表示在區間(xi，xi+1］上沒有發生精度故障的事件。則觀測到樣本所代表的事件可以表示為Bi，因此根據NHPP過程理論:

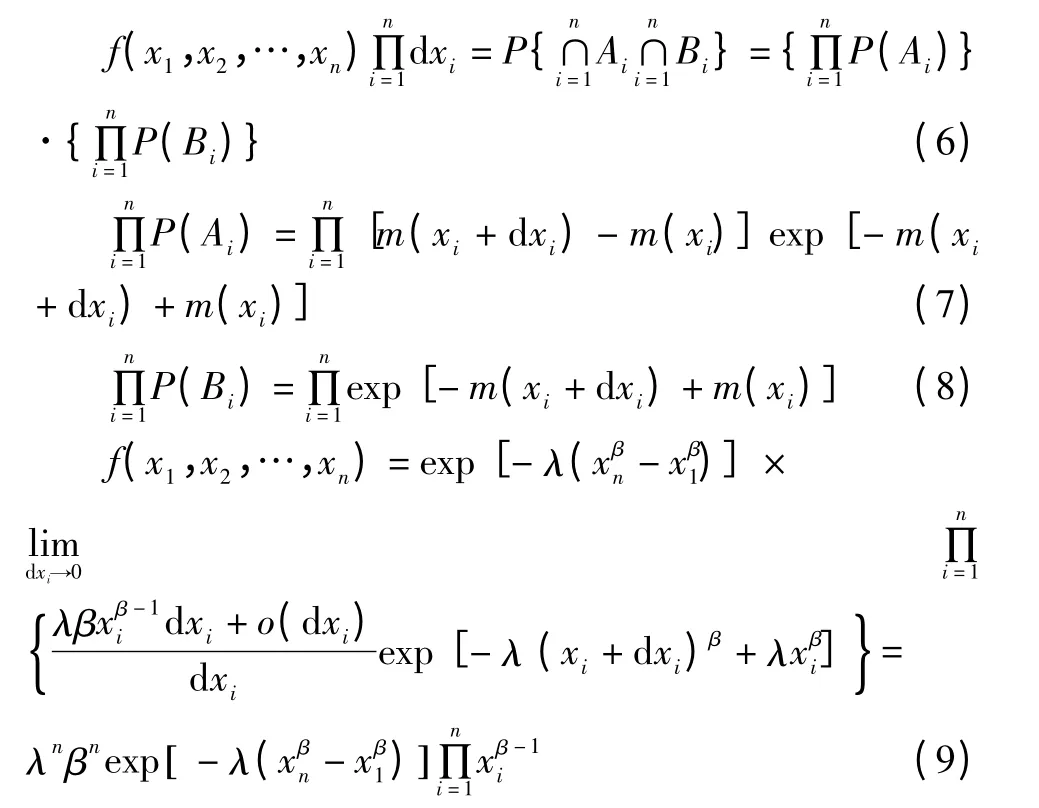
對應的對數似然函數:

則可以得到似然函數偏微分方程組:

根據上述方程組，可以得到λ，β最大似然估計值分別是:

則式(14)化簡為:

該式是一個典型的非線性方程，運用MATLAB軟件可以進行求解。

2 進給系統精度保持性試驗

2．1 試驗臺設計

為了在實驗室條件下模擬其精度隨工作時間的衰減變化過程，進行加速壽命試驗可以在較短時間內使進給系統精度故障暴露出來。本試驗方案基于恒定應力加速壽命試驗理論，設計了滾動直線導軌副試驗系統，通過氣缸對進給試驗臺施加軸向負載。最終搭建的試驗臺實物圖如圖1所示。

圖1 試驗臺實物圖

2．2 進給系統軸線定位精度測量方法

伺服電機按照編程指令位置，驅動工作臺沿著軸線運動到一系列的目標位置Pi，并在各目標位置停留足夠的時間以便測量和記錄實際位置。參照標準規定，本方案在420 mm的進給軸線上選取5個點作為測量點，在每個點重復測量5次偏差，測量間距分別是:9，98，102，97，103，11。測量方案如圖2所示。

圖2 精度測量方案

試驗過程中，進給系統以往復加載跑合1 000次為一個測量周期，進行一次定位精度的測量，實驗總共跑合1 200個測量周期，累積跑合距離504 km。以遠離電機的方向為正方向，布置的測量點按照正方向依次為(P1，P2，P3，P4，P5)。試驗暫不分析由反向間隙產生的誤差，主要研究單向定位精度。

3 數據處理與驗證

3．1 數據預處理

本次計算取前1 000次精度測量結果，此時進給系統累計跑合420 km，相對于設計壽命470 km而言，此次的試驗周期較長，可以反映出進給系統定位精度隨行程的變化規律。根據試驗數據的測量結果，以定位精度單向增大5μm為一個精度故障事件，共統計得到47次精度故障事件。分別記錄每次精度故障時的累積跑合次數ki(i=1，2，3，…，47)如表1所示。

表1 故障累積跑合次數ki記錄表

累積行程增量xi(i=1，2，3，…，47)與累積跑合次數ki(i=1，2，3，…，47)關系式:

3．2 參數估計結果

根據公式(12)及(15)，以累積跑合次數ki(i=1，2，3，…，47)作為樣本值，計算得到:

β=0．655，λ=0．537

則失效率函數:

均值函數:

計算的失效率函數與測量結果擬合情況如圖3所示。

圖3 失效率擬合曲線

根據分析結果，可以做出以下推斷:

(1)在跑合初期，進給系統處于磨合期，隨著跑合次數的增加失效率逐漸降低;當跑合次數超過300次后，失效率趨于穩定，進給系統進入穩定期。

(2)進給系統在跑合k次后的定位精度預測公式為:

其中:A0為進給系統初始精度，μm。

4 結論

運用基于AMSAA模型的非齊次泊松過程對定位精度隨累積跑合行程的變化規律及其分布函數進行了擬合，根據實驗數據對精度保持性模型進行了參數估計，得到失效率函數與均值函數，推導出精度預測公式，并進行了驗證。

［1］楊兆軍，陳傳海，陳菲，等．數控機床可靠性技術的研究進展［J］．機械工程學報，2013，49(6):89-98．

［2］ALTINTAS Y．Manufacturing Automation:Metal Cutting Mechanics，Machine Tool Vibrations，and CNC Design［M］．Cambridge:Cambridge University Press，2012．

［3］仇健，張凱，李鑫，等．國內外數控機床定位精度對比分析研究［J］．組合機床與自動化加工技術，2013(8):1-3．

［4］屠國俊，陶衛軍，馮虎田，等．滾動功能部件可靠性研究及其關鍵技術［J］．制造技術與機床，2011(4):17-19．

［5］韋富基，譚順學．高精度數控機床伺服進給系統精度研究［J］．制造業自動化，2012，34(9):69-71．

［6］黃祥瑞．可靠性工程［M］．北京:清華大學出版社，1990．

［7］A C普羅尼科夫．數控機床的精度與可靠性［M］．李昌琪，遇立基，譯．北京機械工業出版社，1987．

［8］王智明，楊建國，王國強，等．多臺數控機床最小維修的可靠性評估［J］．哈爾濱工業大學學報，2011，43(7):127-130．

［9］杜振華，趙宇，黃敏．基于AMSAA模型的研制試驗數據可靠性綜合評估［J］．北京航空航天大學學報，2003，29(8):745-748．

［10］VAN Dyck J，VERDONCK T．Precision of Power-law NHPPEstimates for Multiple Systems with Known Failure Rate Scaling［J］．Reliability Engineering＆System Safety，2014，126:143-152．