基于多孔彈性介質(zhì)理論的高濃流漿箱鋸齒形流道仿真模擬

董茜茜， 剛芹果

（河北大學(xué) 建筑工程學(xué)院，河北 保定 071002）

0 引言

基于對(duì)理論和實(shí)驗(yàn)結(jié)果的研究，日本制漿與造紙技術(shù)協(xié)會(huì)設(shè)計(jì)了鋸齒形高濃流漿箱［1］。文獻(xiàn)［1］提出了4種不同結(jié)構(gòu)形式的鋸齒形流道。文獻(xiàn)［2］指出濃度超過10%時(shí)，紙漿內(nèi)纖維絮聚形成多孔網(wǎng)絡(luò)狀，可以當(dāng)做多孔介質(zhì)［2］。文獻(xiàn)［3］、［4］分別對(duì)中高濃紙漿的孔隙率和滲透率進(jìn)行了測定。

本文基于文獻(xiàn)［1］～文獻(xiàn)［4］的研究結(jié)果，根據(jù)多孔彈性介質(zhì)理論，運(yùn)用有限元分析軟件ABAQUS，對(duì)不同結(jié)構(gòu)形式的鋸齒形流道進(jìn)行模擬仿真，得到高濃紙漿的孔隙率、孔壓、Mises應(yīng)力等，為進(jìn)一步設(shè)計(jì)優(yōu)化高濃流漿箱提供了又一新的方法。

1 多孔彈性介質(zhì)理論

1.1 多孔彈性介質(zhì)概念

多孔介質(zhì)是指由多相物質(zhì)所占據(jù)的空間，也是多相物質(zhì)共存的一種組合體；從任一相來說，其它相均彌散在其中，故又稱多孔材料。其中，固體相稱為固體骨架；沒有固體骨架的那部分空間稱作孔隙，它常由液體或氣體或氣液兩相占有［5］。考慮固體骨架的線彈性時(shí)，稱為多孔彈性介質(zhì)。

1.2 多孔彈性介質(zhì)模型［6］

（1）應(yīng)力-應(yīng)變關(guān)系：

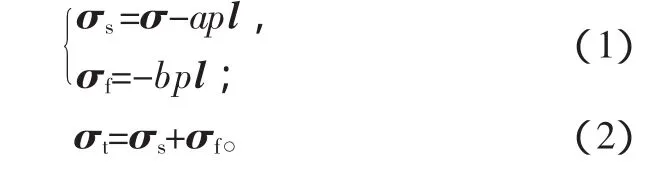
式中：σs、σf、σt分別為骨架、液相和總應(yīng)力張量；p 為液體壓力；a、b分別為骨架和液相的體積分?jǐn)?shù)，a+b=1；σ為有效應(yīng)力張量；l為單位張量。

骨架的變形與強(qiáng)度的變化都只取決于有效應(yīng)力。骨架具有線彈性，根據(jù)胡克定律有

式中：ε為彈性應(yīng)變；C為彈性張量。對(duì)于各向同性體，表征材料彈性性質(zhì)的參數(shù)有2個(gè)，即彈性模量和泊松比。

2）連續(xù)性方程。

仲裁庭認(rèn)為,埃及政府基于公共目的的征收行為是合法的，這一點(diǎn)并無爭議,但征收目的的合法性并不當(dāng)然地免除政府承擔(dān)補(bǔ)償?shù)牧x務(wù)。仲裁庭對(duì)補(bǔ)償金額的標(biāo)準(zhǔn)進(jìn)行了詳細(xì)分析：(1)對(duì)于投資者投入的資金(本金和貸款)，應(yīng)當(dāng)予以補(bǔ)償。(2)項(xiàng)目開發(fā)的費(fèi)用。仲裁庭認(rèn)為，SPP公司所要求的開發(fā)費(fèi)用的補(bǔ)償過高，由于并非所有索賠的費(fèi)用都妥善記錄在案，因此對(duì)于收款人不明確的開發(fā)費(fèi)用不予補(bǔ)償。(3)訴訟和仲裁的相關(guān)費(fèi)用。只賠償與仲裁直接相關(guān)的訴訟費(fèi)用。(4)商業(yè)機(jī)會(huì)的喪失。仲裁庭認(rèn)可了SPP公司主張的商業(yè)機(jī)會(huì)損失，即對(duì)于投資項(xiàng)目價(jià)值的合理預(yù)期收益予以賠償。

骨架和液相都為不可壓縮，多孔彈性介質(zhì)模型的連續(xù)性方程為

其中，Vs、Vf分別為骨架和液相的速度向量。

3）滲流方程和平衡方程：

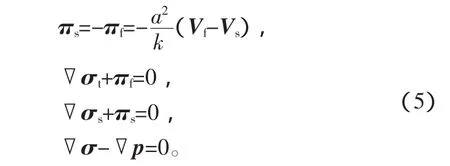
其中，πs、πf分別為骨架和液相的體力向量，k為滲透率。

1.3 定解條件

1）初始條件。

只需設(shè)定體積分?jǐn)?shù)，其他參數(shù)為0。在本次模擬中，只需設(shè)定紙漿濃度。

2）邊界條件。

應(yīng)力邊界條件為

2 不同結(jié)構(gòu)的鋸齒形流道的仿真模擬

文獻(xiàn)［1］提出的新設(shè)計(jì)的鋸齒形流道是由曲面形突擴(kuò)和漸縮區(qū)所組成，如圖1所示。每個(gè)流道由具有相同形狀的3個(gè)單元串聯(lián)而成，每個(gè)單元由“杯”和“角”組成，在“杯”中，曲面是向外凸的，在“角”中，曲面是向內(nèi)凹的［1］。

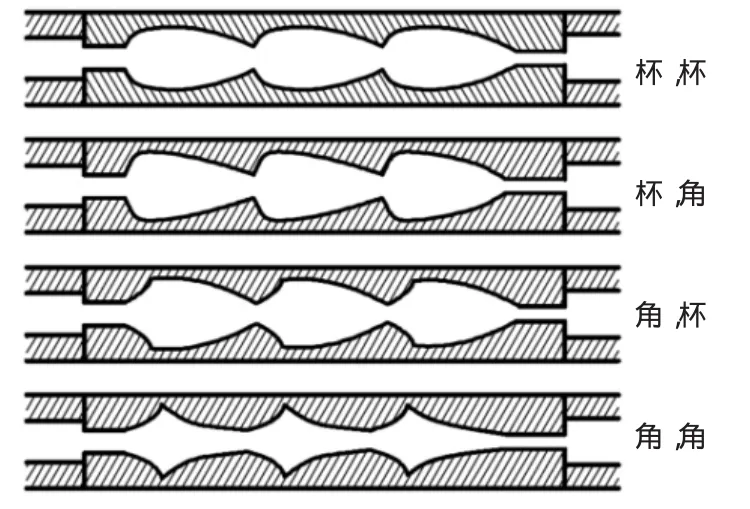
圖1 不同結(jié)構(gòu)的鋸齒形流道

2.1 分析過程

本次研究對(duì)象是濃度為12%的紙漿。根據(jù)文獻(xiàn)［3］，濃度為12%的紙漿的孔隙率為10.5%，相應(yīng)的孔隙比為0.117；根據(jù)文獻(xiàn)［4］，濃度為12%的紙漿的滲透率k為9.75×10-6m/s；骨架的彈性模量E設(shè)為80 MPa，泊松比μ設(shè)為0.48。

以“杯，杯”結(jié)構(gòu)為例，根據(jù)其幾何結(jié)構(gòu)和特性，計(jì)算模型如圖2所示，劃分網(wǎng)格如圖3所示。紙漿從1處進(jìn)入流道，采取壓力進(jìn)口，壓力設(shè)為P1=1 000 Pa；紙漿從5處流出流道，采取自由邊界。運(yùn)用ABAQUS軟件進(jìn)行求解。

2.2 結(jié)果分析

通過計(jì)算可以得到紙漿在不同結(jié)構(gòu)型式流道中的孔隙率、孔壓、Mises應(yīng)力等數(shù)據(jù)。由于孔隙率能反映出紙漿中纖維在流道中的分布情況，本次模擬只對(duì)孔隙分布進(jìn)行分析。不同結(jié)構(gòu)形式流道的孔隙分布如圖4～圖7所示。

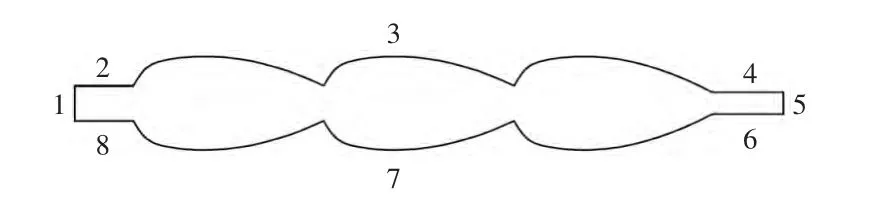
圖2“杯，杯”型結(jié)構(gòu)流道計(jì)算模型

圖3 網(wǎng)格劃分

圖4“杯，杯”型結(jié)構(gòu)流道中，紙漿孔隙分布

圖5“杯，角”型結(jié)構(gòu)流道中，紙漿孔隙分布

圖6“角，杯”型結(jié)構(gòu)流道中，紙漿孔隙分布

圖7“角，角”型結(jié)構(gòu)流道中，紙漿孔隙分布

通過得到的紙漿在不同結(jié)構(gòu)型式的流道中的孔隙分布圖可知，在流道的突擴(kuò)處和漸縮處，紙漿孔隙率變化較大，紙漿纖維分布不均勻程度增加。突擴(kuò)處對(duì)紙漿孔隙率的影響大于漸縮處對(duì)紙漿孔隙率的影響，突擴(kuò)處對(duì)紙漿纖維的分布均勻性的影響大于漸縮處對(duì)紙漿纖維的分布均勻性的影響。

紙漿在“杯，角”型和“角，杯”型結(jié)構(gòu)流道中，孔隙率變化很小，紙漿中纖維分布均勻；紙漿在“杯，杯”型和“角，角”型結(jié)構(gòu)流道中，孔隙率變化明顯，紙漿中纖維分布不均勻程度增加。

3結(jié)語

運(yùn)用ABAQUS仿真軟件對(duì)不同型式高濃流漿箱鋸齒形流道的仿真研究，得到紙漿的孔隙率。該結(jié)果與文獻(xiàn)［1］中的實(shí)驗(yàn)結(jié)果基本一致。

本次的模擬中，將紙漿纖維當(dāng)作各向同性體。中高濃紙漿中，纖維絮聚、纏結(jié)嚴(yán)重，纖維具有各向異性的特點(diǎn)；但在已有的研究中，并沒有對(duì)纖維各向異性的特性參數(shù)進(jìn)行測定。這也為以后的實(shí)驗(yàn)研究提供了一個(gè)新的方向。

［1］ 陳克復(fù).中高濃制漿造紙技術(shù)的理論與實(shí)踐［M］.北京：中國輕工業(yè)出版社，2007.

［2］ 宣征南，陳克復(fù)，陳奇峰.紙漿多孔介質(zhì)特性的實(shí)驗(yàn)研究［J］.湖北造紙，2006（4）：8-10.

［3］ 宣征南，高麗兵，陳克復(fù).中高濃紙漿孔隙率測定的研究［J］.中華紙業(yè)，2007，28（7）：31-33.

［4］ 高麗兵，宣征南，侯來靈.中高濃紙漿滲透率的研究［J］.茂名學(xué)院學(xué)報(bào)，2007，17（1）：38-40.

［5］ 林瑞泰.多孔介質(zhì)傳熱傳質(zhì)引論［M］.北京：科學(xué)出版社，1995.

［6］ 竇長永.關(guān)節(jié)軟骨纖維增強(qiáng)多孔彈性力學(xué)特性研究［D］.深圳：哈爾濱工業(yè)大學(xué)深圳研究生院，2011.

［7］ 貝爾.多孔介質(zhì)流體動(dòng)力學(xué)［M］.北京：中國建筑工業(yè)出版社，1983.