基于迭代積分粒子濾波的目標(biāo)跟蹤算法*

毛少鋒,馮新喜,鹿傳國(guó),危 璋

(1 空軍工程大學(xué)信息與導(dǎo)航學(xué)院,西安 710077;2 95806部隊(duì),北京 100000)

基于迭代積分粒子濾波的目標(biāo)跟蹤算法*

毛少鋒1,馮新喜1,鹿傳國(guó)2,危 璋1

(1 空軍工程大學(xué)信息與導(dǎo)航學(xué)院,西安 710077;2 95806部隊(duì),北京 100000)

針對(duì)粒子濾波在非線性目標(biāo)跟蹤中存在粒子退化的問題,提出一種迭代積分粒子濾波的目標(biāo)跟蹤算法。該算法從改進(jìn)重要性函數(shù)的角度入手,在積分卡爾曼濾波的基礎(chǔ)上,通過高斯牛頓迭代的方法進(jìn)行量測(cè)更新,并對(duì)粒子集合中的粒子進(jìn)行迭代積分卡爾曼濾波,使得構(gòu)造的重要性函數(shù)更加貼近真實(shí)后驗(yàn)分布。仿真結(jié)果表明,與粒子濾波算法、積分粒子濾波算法相比,該算法在有效改善非線性目標(biāo)跟蹤中粒子退化的同時(shí),提高了跟蹤精度。

高斯牛頓迭代;積分卡爾曼濾波;重要性函數(shù);非線性目標(biāo)跟蹤

0 引言

現(xiàn)代戰(zhàn)場(chǎng)環(huán)境中,通過角度獲得的目標(biāo)數(shù)據(jù)信息大都是非線性量測(cè),其跟蹤實(shí)質(zhì)就是利用角度信息來估計(jì)目標(biāo)的運(yùn)動(dòng)狀態(tài)[1]。而粒子濾波(particle filter,PF)[2]可以較好的解決這一非線性濾波估計(jì)問題。

然而粒子退化問題一直是影響粒子濾波精度的一個(gè)重要方面。粒子濾波使用先驗(yàn)概率密度作為重要性函數(shù),沒有考慮最新的量測(cè)信息,使得狀態(tài)估計(jì)存在較大誤差[2]。因此,文獻(xiàn)[3]采用擴(kuò)展卡爾曼濾波(extended kalman filter,EKF)產(chǎn)生重要性函數(shù),但是EKF需要進(jìn)行求導(dǎo)運(yùn)算,容易引入截?cái)嗾`差;文獻(xiàn)[4]采用的是無跡卡爾曼濾波(unscented kalman filter,UKF),UKF需要設(shè)計(jì)合理的Sigma點(diǎn),否則可能導(dǎo)致濾波發(fā)散;文獻(xiàn)[5]利用迭代擴(kuò)展卡爾曼濾波(iterated extended kalman filter,IEKF),運(yùn)用高斯-牛頓迭代方法進(jìn)行線性化時(shí)誤差較大,精度要求較高時(shí)也難以滿足需求;文獻(xiàn)[6]采用容積卡爾曼濾波(cubature kalman filter,CKF),CKF一般在高維情況下有較好的實(shí)時(shí)性,維數(shù)較低時(shí)效果不是很好。

針對(duì)以上問題,文中利用高斯牛頓迭代方法[7]對(duì)積分卡爾曼濾波(quadrature kalman filter,QKF)[8]的量測(cè)進(jìn)行迭代更新,構(gòu)造重要性函數(shù),提出一種迭代積分粒子濾波(iterated quadrature particle filter,IQPF)算法。該算法通過高斯牛頓迭代對(duì)QKF算法進(jìn)行迭代處理,使得迭代QKF產(chǎn)生的重要性密度函數(shù)更加接近真實(shí)后驗(yàn)概率分布。仿真結(jié)果表明,該算法有效的提高了目標(biāo)的跟蹤精度。

1 非線性目標(biāo)跟蹤模型

文中以二維無源傳感器目標(biāo)跟蹤系統(tǒng)為例。此時(shí),無源傳感器只提供角度信息,具體的幾何關(guān)系如圖1所示。

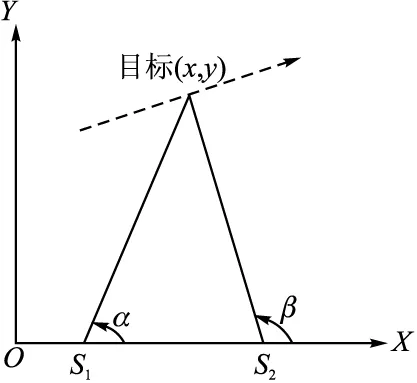
圖1 目標(biāo)與傳感器之間的幾何關(guān)系

對(duì)于勻速運(yùn)動(dòng)目標(biāo),運(yùn)動(dòng)模型可以寫為:

X(k)=FX(k-1)+W(k-1)

(1)

式中:F為狀態(tài)轉(zhuǎn)移矩陣;W(k)為過程高斯白噪聲,服從N(0,Q),Q為協(xié)方差矩陣。

目標(biāo)跟蹤模型的量測(cè)方程為:

Z(k)=h(X(k))+V(k)= [α(k)β(k)]T+V(k)

(2)

(3)

(4)

其中：α(k)、β(k)分別為傳感器1和2的方位量測(cè)值。X=(x(k),y(k))為目標(biāo)在k時(shí)刻的位置坐標(biāo),S1=(x1(k),y1(k))為傳感器1在k時(shí)刻的位置坐標(biāo),S2=(x2(k),y2(k))為傳感器2在k時(shí)刻的位置坐標(biāo)。V(k)為觀測(cè)噪聲,服從N(0,R),而R為量測(cè)噪聲協(xié)方差矩陣。

從量測(cè)方程中可以看出,這是一個(gè)典型的非線性問題,需要通過非線性濾波技術(shù)來獲得優(yōu)估計(jì),下面給出迭代積分粒子濾波跟蹤算法。

2 基于迭代的積分粒子濾波算法

2.1 QKF算法

2007年A.Ienkaran[8]等提出的QKF濾波算法通過使用求積分的原則計(jì)算非線性隨機(jī)變量的均值和協(xié)方差,避免了求導(dǎo)運(yùn)算,并且在低維情況下有較好的濾波效果。同時(shí)它除了具有UKF的優(yōu)點(diǎn)以外,采樣點(diǎn)數(shù)還可以根據(jù)不同的系統(tǒng)要求而改變,具體的算法流程見文獻(xiàn)[9]。

2.2 迭代QKF的量測(cè)更新

然而QKF算法對(duì)模型具有較強(qiáng)的依賴性,且對(duì)濾波的初始條件比較敏感,因此每次迭代相比上一步迭代能否更逼近理想值是不確定的。而迭代QKF利用觀測(cè)更新得到的狀態(tài)估計(jì),對(duì)系統(tǒng)的非線性量測(cè)方程進(jìn)行線性化,這樣每次迭代都采用最新的迭代值,可以有效的減少Q(mào)KF算法線性化過程中帶來的誤差。

高斯牛頓迭代主要用來求解非線性最小二乘問題。由于QKF屬于一種高斯次優(yōu)濾波算法,其中所包含的隨機(jī)量符合高斯分布,因此,可使用最大后驗(yàn)估計(jì)來計(jì)算更新狀態(tài)。

利用最小均方誤差估計(jì)準(zhǔn)則,可得目標(biāo)狀態(tài)的估計(jì)值為:

(5)

根據(jù)貝葉斯理論,后驗(yàn)概率為:

預(yù)測(cè)概率為:

(7)

其中,p(Zk|Xk)為似然概率,由量測(cè)方程和噪聲協(xié)方差矩陣確定。Bell指出卡爾曼濾波的量測(cè)更新可以表示為一個(gè)求極大后驗(yàn)估計(jì)的問題。經(jīng)過上面的分析,也就是求極大似然估計(jì)的問題,即極小化的“費(fèi)用函數(shù)”[10],這樣就可以將問題轉(zhuǎn)化為求下列函數(shù)的極小值:

(8)

用觀測(cè)量和狀態(tài)預(yù)測(cè)這兩個(gè)相互獨(dú)立的隨機(jī)量構(gòu)造了一個(gè)偽觀測(cè)量:

(9)

則此觀測(cè)量同樣為高斯隨機(jī)變量,均值和方差分別表示為:

E(Xk)=[h(Xk)Xk]T

(10)

V=diag([RP])

(11)

則式(8)可表示為:

(12)

令STS=V-1,L(Xk)=S[Z-E(Xk)],則有:

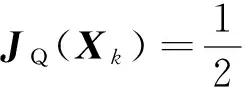
(13)

根據(jù)上式可以看出,QKF的量測(cè)更新則轉(zhuǎn)化為最小二乘問題,按照高斯牛頓方法,對(duì)于目標(biāo)函數(shù)JQ(Xk),高斯牛頓迭代可表示為:

(14)

其中i為迭代次數(shù),函數(shù)L(Xk)的一階導(dǎo)數(shù)為:

(15)

因此,將式(15)代入式(14),整理可得到迭代QKF的量測(cè)更新方程為:

同時(shí)可得到迭代QKF的協(xié)方差矩陣方程為:

(17)

2.3 IQPF算法

通過對(duì)粒子集合中的每個(gè)粒子進(jìn)行迭代QKF濾波,來產(chǎn)生粒子濾波的重要性函數(shù),使得粒子的分布更接近狀態(tài)的后驗(yàn)概率分布。

IQPF中粒子采樣的具體步驟如下:

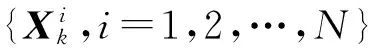
(18)

(19)

則歸一化權(quán)值為:

(20)

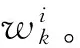
5)重采樣,根據(jù)有效粒子數(shù)和預(yù)設(shè)門限來判斷是否需要重采樣,得到等權(quán)值粒子集。

(21)

(22)

3 仿真分析

為了驗(yàn)證算法的有效性,通過兩組實(shí)驗(yàn),對(duì)IQPF算法和PF算法、QPF算法的性能進(jìn)行對(duì)比分析。

實(shí)驗(yàn)1:通過一組典型的一維非線性模型估計(jì)問題驗(yàn)證IQPF算法的濾波性能,設(shè)系統(tǒng)模型的狀態(tài)方程和觀測(cè)方程為:

Xk=1+sin (0.4πk)+0.5Xk-1+wk-1

式中：過程噪聲服從Gamma分布,wk～Gamma(3,2),觀測(cè)噪聲服從正態(tài)分布,Vk～N(0,0.000 1),初始狀態(tài)X0=1,粒子數(shù)為N=200,蒙特卡羅實(shí)驗(yàn)仿真次數(shù)為50次,重采樣部分采用殘差采樣法,仿真時(shí)間為T=60 s,迭代QKF采用的積分點(diǎn)數(shù)為m=3。

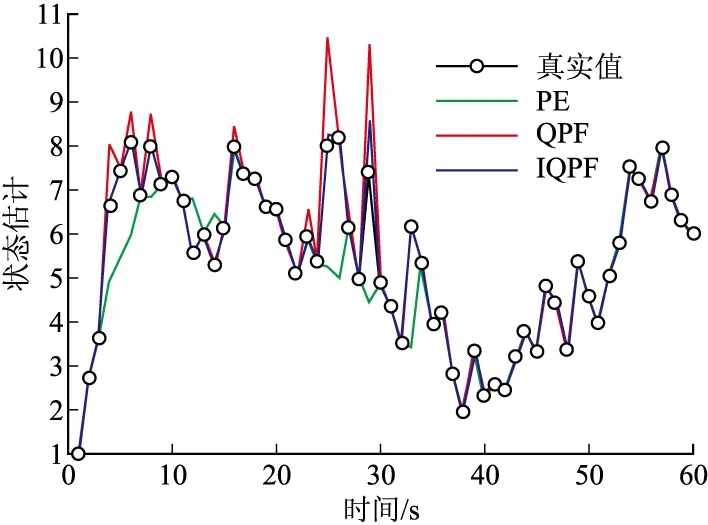
圖2 系統(tǒng)狀態(tài)估計(jì)

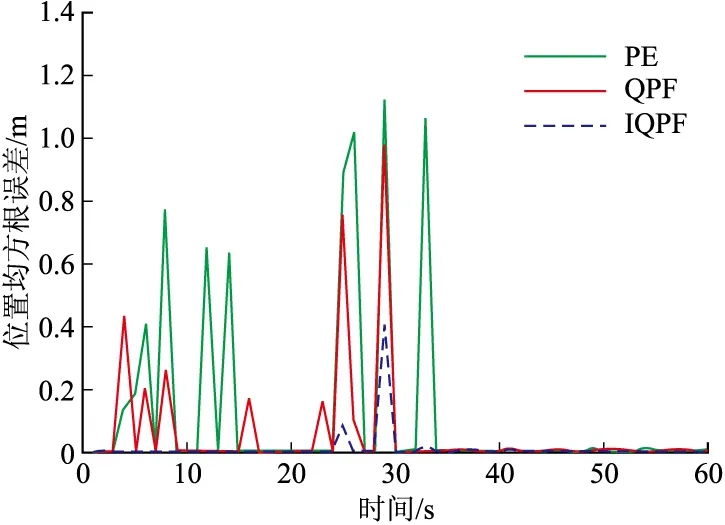
圖3 位置均方根誤差

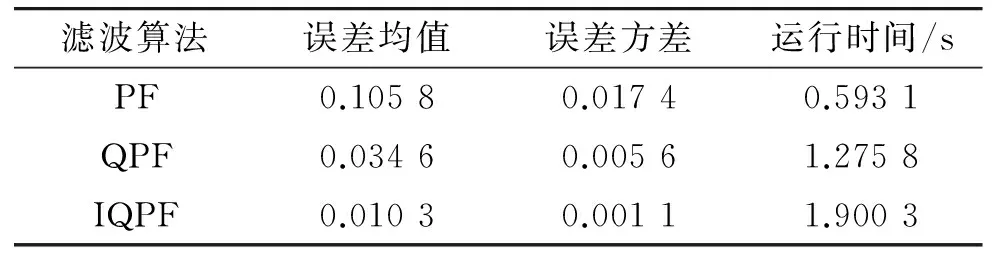
表1 各算法均方根誤差的均值和方差

圖2為各種算法的狀態(tài)估計(jì)曲線,圖3為它們的均方根誤差曲線圖,表1為各算法均方根誤差的均值和方差以及平均運(yùn)行時(shí)間。從仿真結(jié)果可以看出,PF算法在進(jìn)行系統(tǒng)狀態(tài)估計(jì)過程中,有時(shí)會(huì)出現(xiàn)較大的偏離,而IQPF相比PF、QPF能夠較好的估計(jì)系統(tǒng)狀態(tài)。此外,從表1可以看出,IQPF的均方根誤差較小,有效改善了濾波估計(jì)的精度,這主要在于IQPF迭代時(shí)選取的是上一次迭代的最新值。

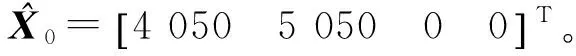
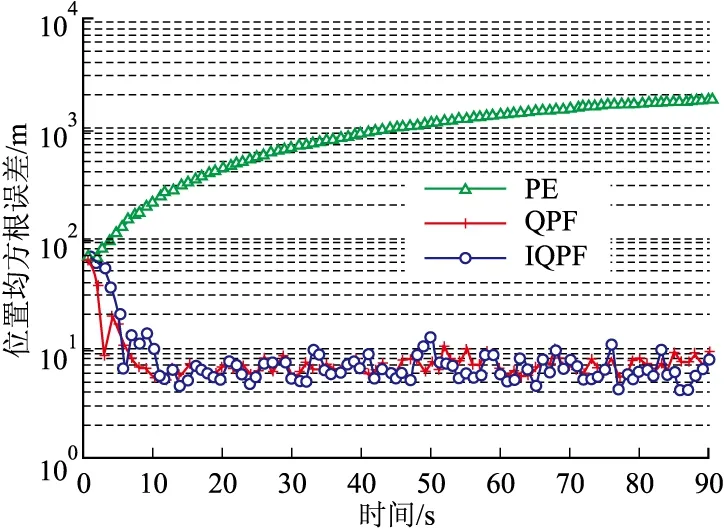
圖4 位置均方根誤差

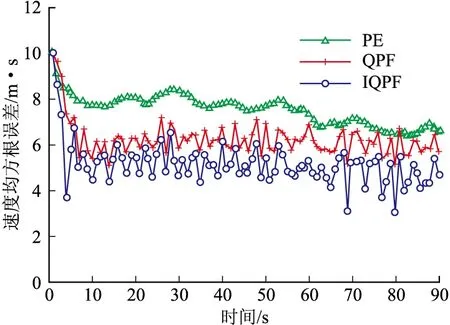
圖5 速度均方根誤差

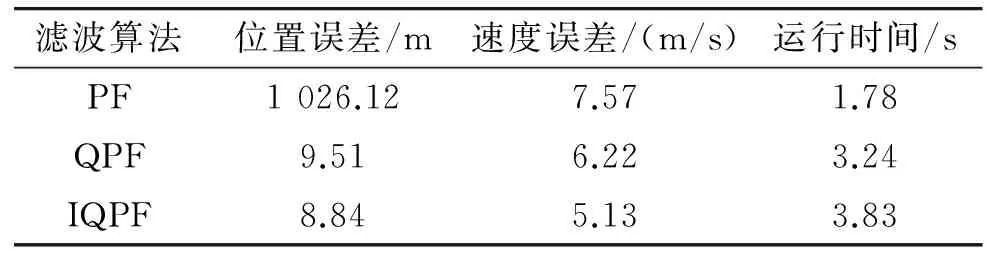
表2 各算法均方根誤差的均值

圖4為位置均方根誤差曲線,圖5它們的速度均方根誤差曲線圖,表2為各算法均方根誤差的均值和方差以及平均運(yùn)行時(shí)間。從仿真曲線以及表2可以看出,PF跟蹤目標(biāo)的誤差較大,難以實(shí)現(xiàn)目標(biāo)的準(zhǔn)確跟蹤,主要在于目標(biāo)濾波的初始狀態(tài)與目標(biāo)真實(shí)狀態(tài)偏離較大,粒子退化現(xiàn)象嚴(yán)重;QPF能夠?qū)崿F(xiàn)目標(biāo)的穩(wěn)定跟蹤,這主要取決于QKF較優(yōu)的非線性逼近性能、數(shù)值精確度以及濾波穩(wěn)定性,使得利用QKF重要性函數(shù)更加貼近于真實(shí)后驗(yàn);IQPF在QKF的基礎(chǔ)上,通過對(duì)量測(cè)方程進(jìn)行迭代處理,每次迭代都采用上一步更新得到的最新的迭代值,使得跟蹤精度相比QPF有了較好的改善,但運(yùn)行時(shí)間也有了些許增加。

4 結(jié)論

文中針對(duì)在非線性目標(biāo)跟蹤中的粒子退化問題,提出了一種迭代的積分粒子濾波目標(biāo)跟蹤算法。利用高斯牛頓迭代對(duì)QKF量測(cè)進(jìn)行迭代更新,使得改進(jìn)后的重要性函數(shù)更加貼近真實(shí)后驗(yàn)分布。仿真實(shí)驗(yàn)表明,文中算法有效地解決了粒子退化以及非線性目標(biāo)跟蹤中的非線性估計(jì)問題,提高了目標(biāo)跟蹤精度。然而如何將所提算法更好的運(yùn)用到多目標(biāo)跟蹤中,將是下一步研究的重要方向。

[1] 張洋, 芮國(guó)勝, 苗俊, 等. 擴(kuò)展容積卡爾曼濾波定位技術(shù)研究 [J]. 光電工程, 2012, 39(4): 38-43.

[2] 胡士強(qiáng), 敬中良. 粒子濾波算法綜述 [J]. 控制與決策, 2005, 20(4): 361-365.

[3] De Freitas N, Niranjan M, Gee A H, et al. Sequential Monte Carlo methods to train neural network models [J]. Neural Computa-tion, 2000, 12(4): 955-993.

[4] Van der Merwe R, Douce A, de Freitas N, et al. The unscented particle filter [R]. Cambridge, UK: Engineering Department, Cambridge University, 2000: 1-45.

[5] 李良群, 姬紅兵, 羅軍輝. 迭代擴(kuò)展卡爾曼粒子濾波器 [J]. 西安電子科技大學(xué)學(xué)報(bào), 2007, 34(2): 233-238.

[6] 孫楓, 唐李軍. Cubature粒子濾波 [J]. 系統(tǒng)工程與電子技術(shù), 2011, 31(11): 2554-2557.

[7] BELL B, CATHEY F. The iterated Kalman filter update as a Gauss-Newton method [J]. IEEE Transactions on Automatic Control, 1993, 38(2): 294-297.

[8] Ienkaran A, Simon H, Robert J E. Discr-etetime nonlinear filtering algorithms using Gauss-Hermite quadrature [J]. Proceedings of the IEEE. 2007, 95(5): 953-977.

[9] 巫春玲, 韓崇昭. 求積分卡爾曼粒子濾波算法 [J]. 西安交通大學(xué)學(xué)報(bào), 2009, 43(2): 25-28.

[10] Freitas J F G, Niranjan M, Gee A H, et al. Sequential Monte Carlo Methods to train neural network models [J]. Neural Computation, 2000, 12(4): 993-995.

[11] 孔云波, 馮新喜, 鹿傳國(guó). 基于改進(jìn)高斯混合粒子濾波的純方位目標(biāo)跟蹤算法 [J]. 宇航學(xué)報(bào), 2012, 33(7): 971-876.

[12] 郝燕玲, 楊峻巍, 陳亮, 等. 平方根容積卡爾曼濾波器 [J]. 彈箭與制導(dǎo)學(xué)報(bào), 2012, 32(2): 169-172.

[13] 鹿傳國(guó), 馮新喜, 張迪, 等. 蒙特卡羅馬爾可夫鏈容積粒子濾波器 [J]. 電子科技大學(xué)學(xué)報(bào), 2012, 41(6): 859-864.

Target Tracking Algorithm Based on Iterative Quadrature Particle Filter

MAO Shaofeng1, FENG Xinxi1, LU Chuanguo2, WEI Zhang1

(1 Information and Navigation College, Air Force Engineering University, Xi’an 710077, China; 2 No.95806 Unit, Beijing 100000, China)

In view of particle degradation problem of nonlinear target tracking, an iterative Quadrature particle filter (IQPF) target tracking algorithm was proposed based on the improved importance function. The algorithm is the basis of the Quadrature Kalman filter (QKF), the Gauss-Newton iteration method is used to make iterative processing, which can take the measurement into account by means of the iterative Quadrature Kalman filter, to make the importance function be closer to the true posterior. The computer simulation results indicate that compared with the particle filter (PF) algorithm and the Quadrature particle filter (QPF) algorithm, this algorithm has better performance in accuracy and effectively solves the particle degradation problem in nonlinear tracking.

Gauss-Newton iteration; Quadrature Kalman filter; importance function; nonlinear tracking problem

2014-03-25

陜西省自然科學(xué)基金(2011JM8023)資助

毛少鋒(1989-),男,陜西澄城人,碩士研究生,研究方向:目標(biāo)跟蹤。

TN953

A