二元非晶體系中α與βJG弛豫在強度與時間上的耦合研究

王 夢，李向前，陳澤明，王利民（燕山大學亞穩材料制備技術與科學國家重點實驗室，河北秦皇島066004）

二元非晶體系中α與βJG弛豫在強度與時間上的耦合研究

王 夢，李向前，陳澤明，王利民?
（燕山大學亞穩材料制備技術與科學國家重點實驗室，河北秦皇島066004）

摘 要：針對由剛性極性分子為溶質和弱極性分子為溶劑構成的二元混合物，通過介電損耗實驗，探究不同摩爾比例下α和β(JG)弛豫在強度和時間上的定量關系。發現α和β(JG)弛豫強度比值Δε(α)/Δε(β)和弛豫時間對數比logτ(α)/logτ(β)隨溫度均表現為線性關系，但是前者斜率隨組分改變明顯，相比之下后者斜率近似相等。也發現具有正混合熱的二元混合體系中β(JG)弛豫時間越長，弛豫強度越高，這不同于純物質中的行為，從極性分子所占自由體積與極性分子的數目兩個方面進行了分析。本研究加深了對β(JG)弛豫物理本質的進一步認識和理解，同時為有效預測β(JG)弛豫的弛豫時間提供了工具。

關鍵詞：玻璃轉變；α弛豫；β(JG)弛豫

0　引言

玻璃轉變是復雜的動力學微觀不均勻過程，可以利用多種弛豫手段進行測量，如介電損耗實驗［1］，動態力學分析實驗［2］、核磁共振光譜儀以及聲子相關光譜［3?4］等手段。介電弛豫技術作為一種常用的動力學研究手段，直觀反映各種弛豫峰位置、形狀而被廣泛應用。在介電弛豫譜中，隨頻率范圍的不同，會出現多個弛豫過程，包括Debye弛豫、α弛豫、慢β弛豫或過剩翅、快β弛豫等［5?7］。由于Debye弛豫存在于特定結構的物質中，所以通常情況下觀察到的弛豫行為有兩種［8?12］：1）α弛豫，具有較慢的動力學行為，起源于分子間的協同運動，涉及到的分子數目較多，對溫度和壓力的依賴性較大；2）β弛豫，具有較快的動力學行為，對于該動力學，目前缺乏一個統一的認識，多數的研究傾向于認為起源于分子的非協同運動，涉及到的分子數目較少，對溫度和壓力的依賴性較小。傳統的觀點認為α弛豫是玻璃轉變的起點，并在此基礎上建立了多個經典理論，如經典的構型熵［13］和自由體積理論［14］，并且認為β弛豫是涉及到分子內的運動，對α弛豫影響很小。但在20世紀70年代，Johari和Goldstein發現在剛性分子中也存在β弛豫［15］，為紀念Johari和Goldstein對β弛豫的貢獻，人們將這一類涉及到整個分子運動的β弛豫［16］稱為βJG弛豫（慢β弛豫），認為是α弛豫的前驅或基礎，影響著物質的不同玻璃轉變性質［17］，對α弛豫和βJG弛豫相關性以及兩種弛豫對玻璃轉變影響的研究成為多年來的熱點問題［18?22］。

Ngai建立的Coupling?Model理論（CM模型）［8，23］，對純物質中α弛豫和βJG弛豫在弛豫時間上的關聯性進行了定量描述：

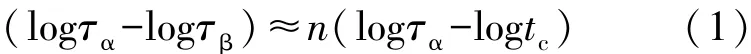
其中，τα和τβ分別是α弛豫和βJG弛豫的弛豫時間，tc約為2 ps，n是耦合參量（0＜n＜1），與Kohl?rausch指數β的關系為n≡1?β。該理論模型認為只要α弛豫峰的峰形和峰位置固定，則βJG弛豫的峰位置就是固定的，對認識βJG弛豫的起源、基本特征等起到了促進作用，加深了人們對βJG弛豫的理解［24?26］。由于βJG弛豫在純物質中的強度比較小，限制了對βJG弛豫進一步的分析研究，因此，多數情況下對βJG弛豫的相關研究是在二元混合體系中進行的［1，6］，如通過介電手段研究水與glycol［27］、alcohol［28］、glycerol［29］、sorbitol［30］、glucose［31］等混合物；glycerol和sorbitol混合物［32］；2?picoline和tri?styrene［33］等混合物，重點分析α弛豫和βJG弛豫動力學隨極性分子組分的變化。但是，對α弛豫與βJG弛豫在弛豫時間、弛豫強度上的相關性以及βJG弛豫時間和弛豫強度之間的關聯性研究卻很少。

本文選擇了剛性且具有一定極性的小分子6?Fluoro?2?methylquinoline（6F2M）作為二元混合物中的溶質，因其分子結構相對簡單，易保證分子的剛性特點，值得注意的是，由于剛性分子不涉及分子內的運動，測出的二級弛豫為βJG弛豫。然而，6?Fluoro?2?methylquinoline（6F2M）中α和βJG弛豫在位置上離得比較近，不利于明顯區分出βJG弛豫，且玻璃形成能力差。由于介電測量只能探測到極性分子的信號，故本文引入弱極性的大分子Triphenylethylene作為溶劑，期望借助該弱極性大分子n值較大的特點，使極性分子6F2M中α和βJG弛豫分離得更明顯，易于分辨出βJG弛豫。在這個前提下，系統分析了α和βJG弛豫在弛豫強度和弛豫時間上的關聯性，研究了βJG弛豫強度和弛豫時間隨溫度和組分變化的規律，給出該混合體系中βJG弛豫的特征和變化規律。該研究有助于建立α和βJG弛豫在強度和時間上的定量關聯，從而實現利用α弛豫的測量結果對βJG弛豫的強度和時間進行有效地預測和評估，解決βJG弛豫因強度低而不容易被準確探測的難題，加深對βJG弛豫變化規律的認識和對βJG弛豫起源問題的理解。

1　實驗部分

1.1實驗藥品制備

本文選擇的藥品為6?Fluoro?2?methylquinoline （6F2M，≥97%，粉末）和Triphenylethylene（TPL，≥99%，粉末），均購買自Sigma?Aldrich公司，使用前未經過任何提純處理。其中，藥品6F2M易于結晶，為了避免混合體系在快速冷卻下晶化，故使6F2M在二元混合物中的摩爾比例較小，因此配制6F2M與TPL摩爾比分別為1∶9、2∶8、3∶7、4∶6的4種混合物。

1.2實驗手段

利用配備有液氮冷卻裝置的Concept80寬頻介電譜儀（德國，Novocontrol）進行等溫測量，掃描頻率范圍為0.01 Hz至10 MHz，溫度范圍為－160 ～400℃，測試樣品加在黃銅極板間，用厚度為25 μm的聚四氟乙烯小條隔開，測試溫度由Novo?control Quatro控制器控制，精度為0.1 K。

1.3實驗測量

由于常溫下兩種藥品為粉末，故將配比好的4種不同比例的混合物進行升溫，待其完全熔化變為混合溶液后滴加至極板之間，并迅速放到已經降溫至－130℃的測量罐中，保證足夠高的冷卻速率，以便得到完全的玻璃態并完成整個弛豫測量過程。通過Havriliak?Negami（HN）［34］方程擬合，對實驗數據進行分析并獲得相應的參數：

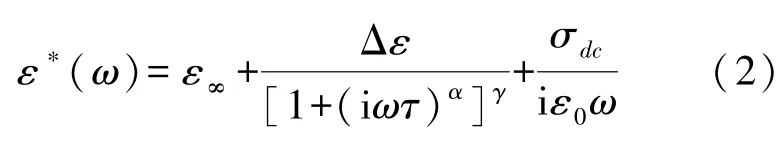
其中，ε∞為高頻介電常量，Δε為介電強度，τ為弛豫時間，α，γ為介電損耗峰的形狀因子，σdc為電導。當γ＝1時，為Cole?Cole（CC）方程［35］，適用于擬合β弛豫，當α＝1時是Cole?Davison（CD）［36］方程。

2　實驗結果與討論

通過介電損耗手段，對摩爾比分別為1∶9、2∶8、3∶7、4∶6的4種6F2M與TPL二元混合物進行測量，得到了玻璃化轉變溫度區間內的介電損耗譜，各自的測量溫度范圍及溫度間隔，如圖1所示。利用HN方程對α弛豫峰進行擬合，如圖1 （a）紅線所示，可以看到，除了低頻處對應的α弛豫峰，在高頻處還有一個明顯的二級弛豫峰，如黑色箭頭所示。由于研究的物質是剛性分子，不涉及分子內的運動，所以該二級弛豫應為βJG弛豫。該弛豫隨溫度的升高移向高頻，并且強度增加。通過比較圖1（a）～（d），可以看到，隨著6F2M組分的增加，混合物中α和βJG弛豫的強度均增強。

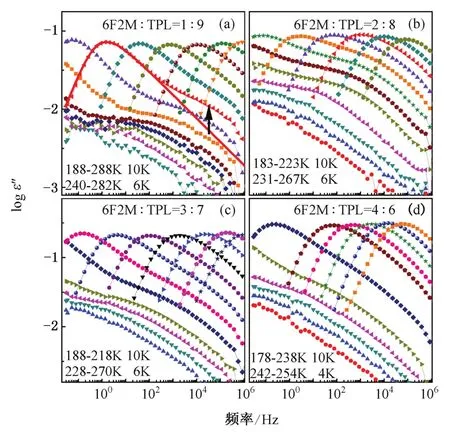
圖1　不同摩爾比例的6F2M和TPL二元混合物介電損耗圖譜Fig.1　Dielectric loss spectra of the mixtures of 6F2M and TPL at different compositions

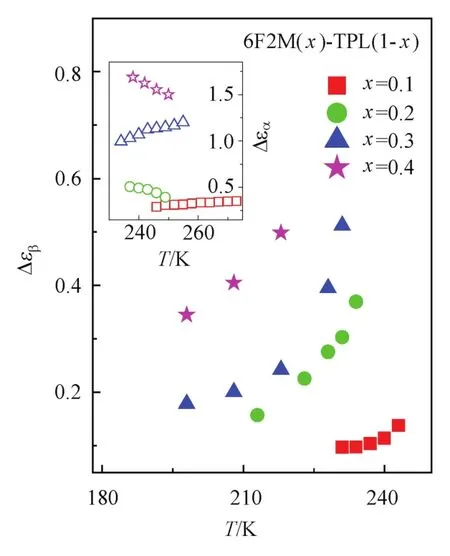
圖2　6F2M和TPL不同摩爾比例混合物中的βJG弛豫強度與溫度的關系Fig.2　Strength of βJGrelaxation in the mixtures of 6F2M and TPL as a function of temperature at different compositions

圖2及其插圖分別給出了βJG弛豫和α弛豫的弛豫強度隨溫度的變化關系。從圖中可以看出：隨著6F2M的組分增加，Δεα和Δεβ均呈現上升的趨勢。但同一組分下，隨著溫度的升高，兩種弛豫的弛豫強度變化并不完全相同。對于βJG弛豫，4種組分下的弛豫強度均隨溫度升高而增加。但是，α弛豫的強度隨溫度的變化則相對復雜。10%6F2M的混合物中Δεα幾乎不變，20%、40% 6F2M的Δεα隨溫度增加而降低，30%6F2M的混合物中Δεα呈現上升的趨勢。造成這一復雜變化趨勢的原因可能源于：隨著6F2M組分的增加，βJG強度增加，α和βJG弛豫的距離也越來越近（如圖1和圖3所示），導致βJG對α弛豫強度影響較大。所以，βJG弛豫時間和弛豫強度的變化對α弛豫產生影響，導致α弛豫復雜的變化趨勢，這暗示了二元混合物中的βJG弛豫的弛豫強度和時間對α弛豫是有影響的。

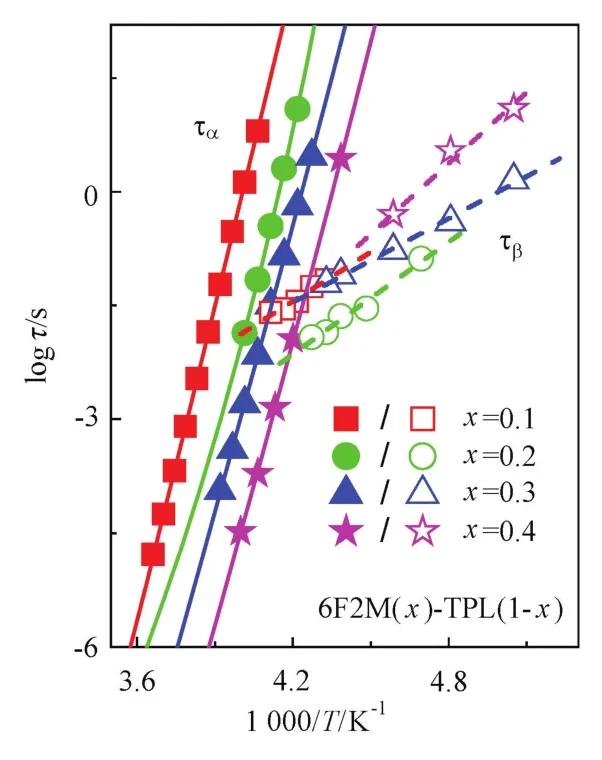
圖3　6F2M與TPL不同摩爾比例混合物的激活能曲線圖Fig.3　Activation plots of the α relaxation and βJGrelaxation in the mixtures of 6F2M and TPL at different compositions

圖3是α弛豫與βJG弛豫的激活能圖，實心圖標表示α弛豫，空心圖標表示βJG弛豫，反映弛豫時間隨溫度倒數的變化規律，從圖中可以更直觀的判定α弛豫和βJG弛豫之間的距離。可以看出，α弛豫與βJG弛豫的弛豫時間隨溫度的變化關系：隨著6F2M組分的增加，｜logτα－logτβ｜越來越小，說明α弛豫和βJG弛豫之間的距離越小。同一組分，隨著溫度的升高，logτα、logτβ逐漸降低可知，α弛豫和βJG弛豫均移向高頻，但由于α弛豫對溫度的依賴性較大，所以α弛豫移向高頻的速度比βJG弛豫快，即圖3中的實線的斜率均高于虛線的斜率。

圖4選擇4種不同組分的二元混合物，α弛豫峰的峰值頻率均在1.65 Hz左右的介電弛豫譜做比較。因為在該頻率處βJG弛豫和α弛豫之間距離相對較遠，從圖中能直觀看出α弛豫和βJG弛豫在弛豫強度和時間上的相對變化，可結合α弛豫峰寬度變化規律分析βJG弛豫對α弛豫的影響。圖中實心符號是實驗測量結果，實線是α弛豫的HN方程擬合結果，得到了對應的形狀因子α，γ，并通過公式β＝（αγ）1/1.23可以求出4種混合物中α弛豫的非指數因子為β1＝0.43、β2＝0.26、β3＝0.40、β4＝0.38。非指數因子β（0＜β≤1）反映的是α弛豫峰的寬窄，β值越大，弛豫峰越窄。通過對比發現隨著極性分子6F2M組分的增加，α和βJG弛豫的強度都逐漸增加，但β值先減小后增大，這表明α弛豫的峰寬度呈先增加后減小的趨勢。由圖2、圖3可知，隨著6F2M組分的增加，α弛豫和βJG弛豫的強度都逐漸增大并且βJG弛豫與α弛豫的距離越來越近。由于隨著極性分子6F2M的增加，20%6F2M的α弛豫強度增加較小，但βJG弛豫的強度增大明顯，且與α弛豫的距離越來越近，導致α弛豫峰變寬。隨著極性分子6F2M數量增加，α弛豫強度也增加，βJG弛豫與α弛豫的距離進一步減小，βJG逐漸變成過剩翅處于α弛豫的高頻處，導致α弛豫峰逐漸變窄。以上結果說明，βJG弛豫強度、位置共同影響了α弛豫的強度和峰寬度。

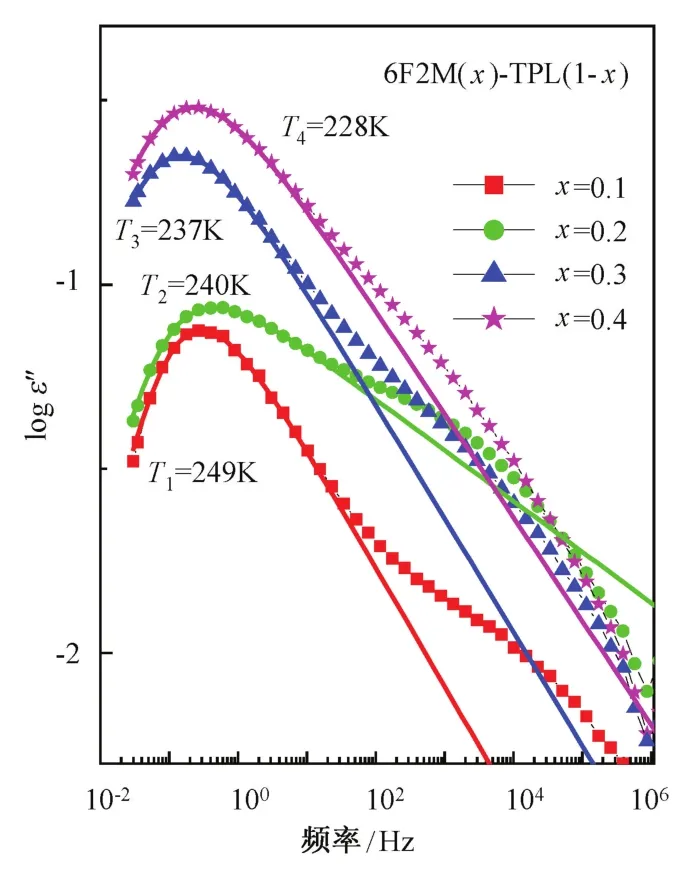
圖4　6F2M和TPL 4種不同組分α弛豫峰值頻率為～1.65 Hz時的介電圖譜Fig.4　Comparison of the dielectric loss spectra for the mixtures of 6F2M and TPL at four representative temperatures and the data are selected to guarantee the α?peak position to be located at～1.65 Hz

為了進一步研究兩種弛豫間的相互關系，進行了不同組分下的兩種弛豫強度和弛豫時間對數的比值隨溫度變化的探究，建立α和βJG弛豫的定量關聯。

圖5（a）表示α和βJG弛豫介電強度比隨著溫度的變化關系，從圖中可以看到，隨著6F2M組分的增加，α和βJG弛豫強度比值呈線性增大的（當6F2M組分為20%時并不是增加的），說明隨組分的增加，兩種弛豫的強度變化并不是同步的，Δεα的增長幅度要大于Δεβ。可以發現α和βJG弛豫強度的比值Δεα/Δεβ隨溫度變化呈線性關系，斜率K1、K2、K3分別為0.346、－0.029、2.171，數值并不相同，且差別較大，難以通過已知組分的強度來預測其他組分的強度。

圖5（b）表示α和βJG弛豫時間對數之比隨溫度的變化關系，對比6F2M為10%、20%、30%的3組混合物結果，α和βJG弛豫時間對數的比值logτα/logτβ隨溫度變化也呈線性關系，更為有趣的是，斜率非常接近，分別為0.049、0.063、0.055。而40%6F2M結果為0.016，相差較大，分析可能的原因是該組分下兩種弛豫的弛豫峰離的很近，難以分開并獲得準確的弛豫時間。這一結果將有助于利用已知組分下的βJG弛豫時間來外推其他組分下的弛豫時間，更深入的研究將在后續工作中完成。

對純物質的研究發現，隨著溫度升高，βJG弛豫的弛豫時間越短，對應的弛豫強度就越大。一般而言，分子運動加快的同時，運動的幅度會加大，運動也越劇烈。為了探究二元混合物中，βJG弛豫的弛豫時間和強度之間的關系是否與已有的發現一致，本文對該體系4種混合物在Tg以下得到的弛豫時間和弛豫強度的關系進行了對比研究。

圖6（a）給出了玻璃轉變溫度Tg以下，混合物中βJG弛豫的弛豫時間與弛豫強度的關系圖。對比4種混合物在0.97Tg處的弛豫時間和弛豫強度（如圖6中空心圖標所示），可以看出隨著6F2M組分的增加，βJG弛豫時間變長，而弛豫強度也逐漸增大，這不同于純物質中βJG弛豫越快，弛豫強度越大的行為。導致這種情況可能的原因有兩種：極性分子的數量和自由體積的差異。從極性分子數量角度分析，組分大的6F2M混合物中的極性分子數量多，即使在動力學較慢的情況下，也可能導致其弛豫強度高于組分小時的βJG弛豫強度。不同組分下的極性分子6F2M質量分數分別為6.53%、13.59%、21.23%、29.54%。當忽略升溫后不同組分下溶液密度的改變時，利用6F2M的質量分數對不同組分的βJG弛豫強度進行歸一化處理，即ΔβJG/ω6F2M，可得對應極性分子數量相等時各組分中βJG弛豫強度，如圖6（b）所示。可以看到，不同組分的βJG弛豫時間和弛豫強度的變化仍與純物質中的弛豫時間和弛豫強度的變化行為不同。初步推測，這可能與混合物中極性分子的自由體積的大小相關。注意到該二元體系可看作為一個體積相對較小的極性分子為溶質溶解到體積較大的弱極性分子中形成的，可以預計這兩個組元之間表現出正的混合熱。盡管整體上體系是混溶的，當極性分子與弱極性分子的比例不同時，極性分子的自由體積也會不同，有關體積上的研究需要進一步開展，以更全面的揭示自由體積對βJG弛豫強度和弛豫時間關聯性的影響。

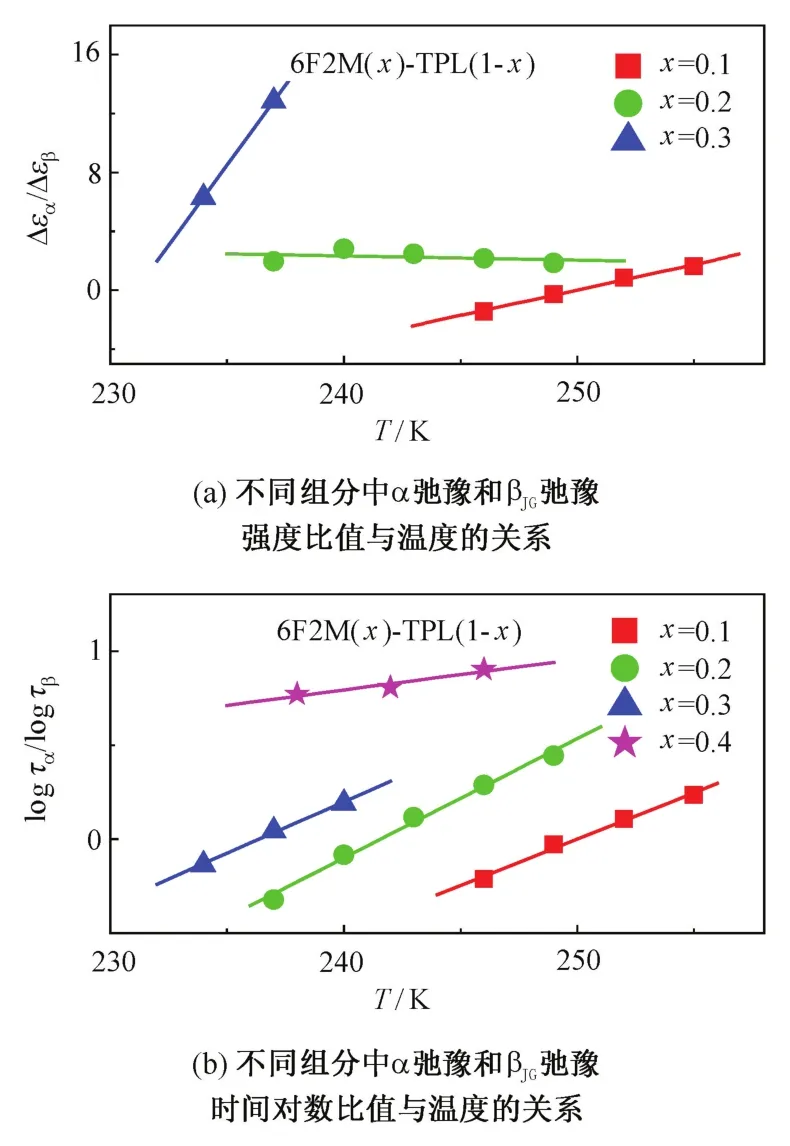
圖5　6F2M與TPL不同組分混合物中α弛豫和βJG弛豫的弛豫強度比值、弛豫時間對數比值與溫度的關系Fig.5　Temperature dependence of the ratios of relation strength Δεα/Δεβand of logarithmic relation time logτα/logτβbetween α and βJGrelaxations in mixtures of 6F2M?TPL at different compositions

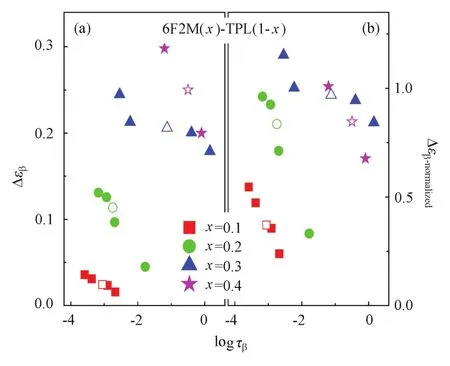
圖6　在Tg以下不同組分的βJG弛豫時間和弛豫強度的關系圖Fig.6　Relation of the relaxation time to relaxation strength for the four mixtures below Tg

3　結論

對具有明顯二級弛豫的6?Fluoro?2?meth?ylquinoline與Triphenylethylene二元混合體系進行研究，通過弛豫強度和弛豫時間的比較，發現βJG弛豫強度和時間均與α弛豫相關。α和βJG弛豫的弛豫時間對數比值隨溫度變化表現為線性關系，這一規律為有效預測βJG弛豫的弛豫時間提供了實用工具。混合體系中βJG弛豫強度與弛豫時間之間表現出更為復雜的關系，不同于純物質中提高的弛豫強度和加快的弛豫時間的同步性行為。可以預計，利用二元混合體系將有助于揭示自由體積對βJG弛豫動力學的影響。

參考文獻

［1］Johari G P Goldstein M.Viscous liquids and the glass transitionⅡ.Secondary relaxations in glasses of rigid molecules J .Journal of Chemical Physics 1970 53 6 2372?2388.

［2］Heijboer J.Physics of Non?crystalline Solids M .Amsterdam North Holland 1965.

［3］Laupretre F Virlet J Bayle J P.Local motions between unequivalent conformations in solid poly cyclohexyl methacrylate A variable?temperature magic?angle carbon?13 nuclear magnetic resonance study J .Macromolecules 1985 18 10 1846?1850.

［4］Fytas G.Relaxation processes in amorphous poly cyclohexyl meth?acrylate in the rubbery and glassy state studied by photon correla?tion spectroscopy J .Macromolecules 1989 22 1 211?215.

［5］胡麗娜 張春芝 岳遠征 等.研究玻璃轉變本質的新起點——玻璃態的慢β弛豫 J .科學通報 2010 55 2 115?131.

［6］Ngai K L.Relaxation and diffusion in complex systems M .New York Springer 2011.

［7］Lunkenheimer P Loidl A.Dielectric spectroscopy of glass?forming materials α?relaxation and excess wing J .Chemical Physics 2002 284 1 205?219.

［8］Ngai K L.Relation between some secondary relaxations and the α relaxations in glass?forming materials according to the coupling model J .Journal of Chemical Physics 1998 109 16 6982?6994.

［9］Casalini R Roland C M.Aging of the secondary relaxation to probe structural relaxation in the glassy state J .Physical Review Letters 2009 102 3 035701.

［10］Ngai K L Paluch M.Classification of secondary relaxation in glass?formers based on dynamic properties J .Journal of Chemical Physics 2004 120 2 857?873.

［11］B?hmer R Diezemann G Geil B et al.Correlation of primary and secondary relaxations in a supercooled liquid J .Physical Review Letters 2006 97 13 135701.

［12］Casalini R Roland C M.Pressure evolution of the excess wing in a Type?B glass former J .Physical Review Letters 2003 91 1 015702.

［13］Adam G Gibbs J H.On the temperature dependence of cooperative relaxation properties in glass?forming liquids J .Journal of Chemical Physics 1965 43 1 139?146.

［14］Cohen M H Turnbull D.Molecular transport in liquids and glasses J .Journal of Chemical Physics 1959 31 5 1164?1169.

［15］Boyer R F.Mechanical motions in amorphous and semi?crystalline polymers J .Polymer 1976 17 11 996?1008.

［16］Johari G P.Intrinsic mobility of molecular glasses J .Journal of Chemical Physics 1973 58 4 1766?1770.

［17］Kudlik A Tschirwitz C Benkhof S et al.Slow secondary relaxation process in supercooled liquids J .Europhysics Letters 1997 40 6 649?654.

［18］Blochowicz T R?ssler E A.Beta relaxation versus high frequency wing in the dielectric spectra of a binary molecular glass former J .Physical Review Letters 2004 92 22 225701.

［19］Capaccioli S Ngai K L.Relation between the α?Relaxation and Jo?hari?Goldstein β?Relaxation of a component in binary miscible mix?tures of glass?formers J .Journal of Physical Chemistry B 2005 109 19 9727?9735.

［20］Cangialosi D Alegria A Colmenero J.?Self?concentration effects on the dynamics of a polychlorinated biphenyl diluted in 1 4?poly?butadiene J .Journal of Chemical Physics 2007 126 20 204904.

［21］Wang L M Richert R.Primary and secondary relaxation time dis?persion in fragile supercooled liquids J .Physical Review B 2007 7 6 06420.

［22］Gao Y Q Chen Z M Tu W K et al.Anomaly in dielectric relaxa? tion dispersion of glass?forming alkoxy alcohols J .Journal of Chemical Physics 2015 142 21 214505.

［23］Ngai K L Capaccioli S.Relation between the activation energy of the Johari?Goldstein β relaxation and Tg of glass formers J .Physi?cal Review E 2004 69 3 031501.

［24］Johari G P Goldstein M.Viscous liquids and the glass transitionⅢ.Secondary relaxations in aliphatic alcohols and other nonrigid molecules J .Journal of Chemical Physics 1972 55 9 4245?4252.

［25］Williams G Watts D C.Molecular motion in the glassy state.The effect of temperature and pressure on the dielectric β relaxation of polyvinyl chloride J .Transactions of the Faraday Society 1971 67 1971?1979.

［26］Williams G Watts D C.NMR Basic principles and progress M .Berlin Springer?Verlag 1971.

［27］Shinyashiki N Sudo S Abe W et al.Shape of dielectric relaxation curves of ethylene glycol oligomer?water mixtures J .Journal of Chemical Physics 1998 109 22 9843?9847.

［28］Sato T Chiba A Nozaki R.Hydrophobic hydration and molecular association in methanol?water mixtures studied by microwave die?lectric analysis J .Journal of Chemical Physics 2000 112 6 2924?2932.

［29］Sudo S Shimomura M Shinyashiki N et al.Broadband dielectric study of α?β separation for supercooled glycerol?water mixture J .Journal of Non?Crystalline Solids 2002 307?310 356?363.

［30］Nozaki R Zenitani H Minoguchi A et al.Dielectric relaxation processes in water?in?sorbitol mixtures J .Journal of Non?Crystalline Solids 2002 307?310 349?355.

［31］Tyagi M Murthy S S N.Dynamics of water in supercooled aqueous solutions of glucose and poly ethylene glycol s as studied by die?lectric spectroscopy J .Carbohydrate Research 2006 341 5 650?662.

［32］Duvvuri K Richert R.Binary glass?forming materials mixtures of sorbitol and glycerol J .Journal of Physical Chemistry B 2004 108 29 10451?10456.

［33］Blochowicz Th Tschirwitz Ch Benkhof St et al.Susceptibility functions for slow relaxation processes in supercooled liquids and the search for universal relaxation patterns J .Journal of Chemical Physics 2003 118 16 7544?7555.

［34］Havriliak S Negami S.A complex plane analysis of α?dispersions in some polymer systems J .Journal of Polymer Science Part C Polymer Symposia 1966 14 1 99?117.

［35］Cole K S Cole R H.Dispersion and absorption in dielectricsⅠ.Alternating current characteristics J .Journal of Chemical Physics 1941 9 4 341?351.

［36］Davision D W Cole R H.Dielectric relaxation in glycerol propylene glycol and n?propanol J .Journal of Chemical Physics 1951 19 12 1484?1490.

Studies of coupling between α and βJGrelaxations in relaxation time and strength in binary glass?forming mixtures

WANG Meng LI Xiang?qian CHEN Ze?ming WANG Li?min
State Key Laboratory of Metastable Materials Science and Technology Yanshan University Qinhuangdao Hebei 066004 China

AbstractDielectric measurements of the binary molecular mixtures composed of a rigid and polar liquid as solute and a non?polar liquid as solvent are performed to explore the correlation of the relaxation time and the relaxation strength of the α and β(JG)relaxa?tions in different compositions.The ratio of the relaxation strength for the α and β(JG)relaxations Δε(α)/Δε(β)is found to increase lin?early with temperature but the slopes differ notably among the mixtures.In contrast where as the ratio of the logarithmic relaxation time for the two relaxations logτ(α)/logτ(β)also shows a linear relation to temperature the slopes basically keep constant enabling the effective prediction of the β(JG)relaxation time.Meanwhile quite different behaviors are found for the relaxation strength and relax?ation time in binary glass forming mixtures when compared with the pure glass formers and the contributions from the free volume and the number of polar molecules in mixtures are discussed.The results would help the further understanding of the physics of the β(JG)relaxation.

Key wordsglass transition α relaxation β(JG)relaxation

作者簡介：王夢（1991?），女，河南濮陽人，碩士研究生，主要研究方向為常壓和高壓下的過冷液體中二級β弛豫動力學；?通信作者：王利民（1973?），男，河北玉田人，博士，教授，博士生導師，主要研究方向為非晶態材料的形成和熱穩定性，Email：limin＿wang＠ysu.edu.cn。

基金項目：國家重點基礎研究發展規劃（973計劃）資助項目（2015CB856805）；國家自然科學基金資助項目（11474247）；河北省自然科學基金資助項目（A2014203260）；河北省教育廳百名優秀人才支持計劃資助項目（BR2?227）

收稿日期：2015?04?03

文章編號：1007?791X（2015）03?0206?07

DOI：10.3969/j.issn.1007?791X.2015.03.003

文獻標識碼：A

中圖分類號：O469