風荷載作用下復剛度阻尼TMD減振結構優化設計

彭凌云，康迎杰，秦 麗，何浩祥

（1.北京工業大學工程抗震與結構診治北京市重點實驗室，北京 100124；2.湖北文理學院建筑工程學院，湖北襄陽 441053）

風荷載作用下復剛度阻尼TMD減振結構優化設計

彭凌云1，康迎杰1，秦 麗2，何浩祥1

（1.北京工業大學工程抗震與結構診治北京市重點實驗室，北京 100124；2.湖北文理學院建筑工程學院，湖北襄陽 441053）

利用復剛度阻尼進行減振的優化設計理論亟需發展。建立具有復剛度阻尼特征的調頻質量阻尼器（TMD）減振結構的動力學方程，并基于定點理論提出了采用復剛度阻尼的TMD結構最優頻率比和最優阻尼比確定方法。對具有復剛度阻尼特征的TMD減振結構在簡諧激勵和平穩隨機激勵下的穩態響應進行了分析。以主結構位移振幅最小為優化條件，推導TMD的阻尼和頻率最優參數的理論公式。結果表明復剛度阻尼TMD的整體減振效果接近于黏滯阻尼減振結構，在相同質量比和一定頻率范圍內，復剛度阻尼比黏滯阻尼可能具有更好的減振效果。對Davenport風速譜下復剛度阻尼TMD減振結構的隨機響應進行分析，結果表明TMD的減振效果要弱于白噪聲作用下的結果，復剛度阻尼TMD減振效果稍遜于黏滯阻尼的情況，但二者結果較接近。在應用TMD減振技術時，采用復剛度阻尼是一種有益的選擇方案。

復剛度阻尼；TMD；穩態響應；隨機振動

目前調頻質量阻尼器（Tuned Mass Damper，TMD）相關的理論與應用研究中大都假定結構和TMD子結構中的阻尼屬性為與變形速度相關的黏滯阻尼。線性黏滯阻尼TMD減振結構的優化設計理論目前也較為成熟，在機械、土木等領域都取得了很成功的應用［1－5］。其中穩態響應對應的最優參數早已獲得經典的理論公式，文獻［5］對TMD的研究歷史、發展及現狀做了非常詳盡的介紹，在此不再贅述。關于非線性黏滯阻尼TMD減振結構的優化設計亦開展一些的研究工作［6－7］，總體上看來相對于線性黏滯阻尼還是具有一定的優勢，但應用時無理論公式指導設計，需通過數值方法求其優化參數。另外，非線性問題對應的最優解大多數情況下與振動幅值相關，適用范圍需加以明確限定。如不加特殊說明，下文中“黏滯阻尼”指的都是線性黏滯阻尼。

關于復剛度阻尼在TMD減振結構中的應用研究遠落后于黏滯阻尼。Snowdon［8］在半個世紀前研究了具有復剛度阻尼TMD減振結構的最優參數，研究表明復剛度阻尼TMD減振結構的效果與線性黏滯阻尼相近，不過該文沒有給出最優參數與質量比的關系式。丁文鏡在文獻［9］中對該文的研究成果做了部分介紹，其后國內外關于減振方面的學術專著中似乎再無此類阻尼的相關介紹。其原因可能是因為能夠提供復剛度阻尼特征的裝置較少，因而未能引起研究人員和工程界的注意。Inaudi等［10－11］提出了一種線性滯回阻尼裝置，該阻尼器的滯回曲線為位于一、三象限的兩個對角三角形，相當于復剛度阻尼與彈性剛度的并聯模型。在此基礎上，Zhou［12］提出了一種具有復剛度阻尼特征的變摩擦阻尼器，但其構造較為復雜。彭凌云等［13－14］則通過更為簡單的方式實現復剛度阻尼，裝置簡單，造價低廉。雖然這些具有復剛度阻尼特征的減振裝置目前離工程應用尚有一定距離，但如果復剛度阻尼TMD的減振效果令人滿意，則可為相關研究人員多提供一種研究思路，可為工程應用再多提供一種有益的選擇。

基于主結構無阻尼的二自由度力學模型，本文對簡諧激勵和白噪聲隨機過程激勵下復剛度阻尼TMD減振結構的動力響應進行了分析，推導了最優參數的理論公式。在具有Dawenport譜特征的隨機風振過程作用下對主結構的功率譜和響應方差進行了計算，對復剛度阻尼和黏滯阻尼兩種TMD的減振效果進行了對比分析。

1 風荷載作用下包含復剛度阻尼結構的運動方程

如圖1所示的主結構無阻尼的二自由度結構力學模型，荷載作用于主結構上，對應風荷載作用于建筑結構的情況，其對應的運動方程見公式（1）。

式中：m0、k0、m1、k1分別為TMD減振結構中主、子結構的質量和剛度，fd為子結構的阻尼力。當采用復剛度阻尼時，計算公式如下所示。式中η為復剛度阻尼的參數kd與子結構剛度k1的比值［15］：

圖1 風荷載作用下二自由度TMD減振結構力學模型Fig.1 Themechanicalmodel of two degree of freedom structure with TMD excited by wind load

2 簡諧激勵下結構位移響應動力放大系數的理論解

定義主、子結構的位移響應的動力放大系數為上式的模，由此可得：

3 根據定點理論求解最優參數

Hahnkamm［16］首次揭示了主結構無阻尼的TMD減振結構中不同子結構阻尼對應的主結構位移響應放大系數隨輸入頻率比g變化的曲線簇中存在公共點，即所謂“定點”，如圖2所示。Den Hartong［17］基于定點理論推導了采用黏滯阻尼TMD結構的最優頻率比和最優阻尼比，其中最優頻率比由兩個公共點處縱坐標相等的條件獲得，最優阻尼比由動力放大系數曲線的峰點與公共點重合求得。本文亦采用此思路推導復剛度阻尼TMD減振結構的最優頻率比和阻尼比。對式（6）中β0分別取η趨于0和無窮的極限值得：

當μ、f為任意給定數值時，上式描述的是子結構阻尼比取0和無窮大條件下的兩條β0（g）曲線，應該有兩個交點，令二者相等整理后可得：

式（8）中g的兩個正根即為“定點”的橫坐標，記為ga、gb，如圖2所示。再將ga、gb分別代入到式（7）中第二式后令二者相等可解得使定點處縱坐標（動力放大系數）相等的最優頻率比與質量比的關系為：

最優頻率比對應的兩個定點橫坐標為：

最優頻率比對應的兩個定點處主結構位移動力放大系數為：

將最優頻率比代入式（6）中第一式中后再求得使定點處放大系數值為局部極大值的阻尼參數，經過較為復雜的推導后可得：

當質量比μ不是太大時，可按文獻［17］的方法定義簡諧激勵下穩態響應對應的最優阻尼參數為：

表1給出了復剛度阻尼TMD減振結構的最優參數，作為對比同時還給出了黏滯阻尼體系的相應結果。

表1 簡諧風振激勵下TMD減振結構穩態響應優化參數Tab.1 Optim ization parameters of steady－state response of structure w ith TMD disturbed by harmonic excitation

從表1中可以看出：

（1）兩種阻尼對應的最優頻率比、定點處縱橫坐標一致。

（2）兩種阻尼對應的最優阻尼參數不同，而且二者計算公式中函數變化趨勢也不同公式中分子部分是μ的一次多項式，而是二次的。

圖2給出的是質量比為0.05、頻率比f＝fopt、不同阻尼條件下主結構位移動力放大系數隨輸入頻率比g的變化曲線，阻尼參數包括復剛度阻尼5種情況（η＝［0，ηa，ηopt，ηb，∞］）和最優黏滯阻尼參數。

從圖2中可以看出：

（1）最優參數條件下，在g值小于第一定點ga的區域，采用復剛度阻尼的TMD減振結構的主結構位移

圖2 簡諧風振作用下主結構位移放大系數曲線Fig.2 The displacement amplification coefficient curve ofmain structure with harmonic wind excitation

放大系數小于采用黏滯阻尼的情況；在g值大于第二定點gb的區域，前者數值大于后者。因此在質量比等于0.05條件下，當激勵頻率小于主結構頻率的89.7% （ga的數值）時，復剛度阻尼減振效果要優于黏滯阻尼；

（2）最優參數條件下，復剛度阻尼TMD減振結構位移放大系數曲線中最大值稍大于黏滯阻尼對應的結果，具體數值分別為6.49和6.41，前者比后者大1.25%。

4 簡諧激勵時定點處其他參數分析

如上所述，在f＝fopt、η＝ηa條件下，圖2中TMD減振結構的主結構位移在定點a，b處相等，下面對兩種阻尼對應的TMD減振結構中其他力學參數加以分析。

將fopt、ηa、ga代入式（5），可分別求得復剛度阻尼TMD減振結構中子結構的變形幅值、相位以及主結構的相位隨質量比的變化關系。見圖3，為便于對比，圖3中同時給出了主結構位移幅值及黏滯阻尼對應的情況。從圖3中可以看出：

（1）在定點處，兩種阻尼對應的主、子結構的振幅和相位數值一致，在特定條件下兩種阻尼可以獲得完全相同的結果。

（2）子結構相對于主結構的位移隨著質量比的增加而減小，但其幅值明顯大于主結構的位移，這體現了所謂“動力吸振”的特點，以子結構的大幅度振動換得主結構振幅的降低；

圖3 簡諧風振作用下定點處主子結構振幅及相位隨頻率比的變化Fig.3 curves of amplitude and phase change with frequency ratio of structure with TMD disturbed by harmonic wind excitation

（3）主子結構的相位有明顯的差異，當質量比為0.01和0.05時二者相位差分別為1.09和1.14，約為π／3，這體現了TMD的“調頻”特點。

在f＝fopt、η＝ηa條件下，ga點對應的子結構最大復剛度阻尼力可按下式計算：

將表1中的相關公式代入式（16），經過化簡后得βfηζ＝1，即在定點處兩種阻尼對應的最大阻尼力也相等。

從上面的分析結果看，復剛度阻尼與黏滯阻尼在定點處的結果是一致的，二者對結構響應的影響相同。

5 平穩白噪聲風振激勵下的最優參數

圖1所示的二自由度結構在平穩白噪聲風振激勵下的位移響應傳遞函數與式（5）具有相同的函數形式，主結構位移響應的傳遞函數可寫為如下形式：

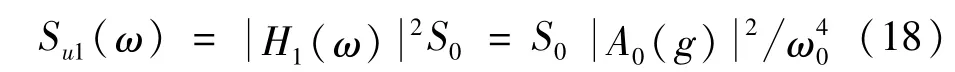
對主結構位移響應功率譜在頻率域內積分可得其響應方差：

將A0（g）代入式（19）后運用留數定理可以得到式（19）理論解，但公式十分復雜。通過數值方法求得使響應方差取得最小值對應的最優阻尼比和頻率比隨質量比變化曲線，采用數值擬合的方法求得相應的最優參數經驗公式如下表所示，為便于對比，表中同時給出了黏滯阻尼TMD減振結構的優化參數的理論公式［9，18］。

表2 平穩白噪聲風振激勵下穩態響應優化參數Tab.2 Optim ization param eters of steady-state response of structure w ith TMD disturbed by stationary white noise process excitation

圖4給出了ζ0＝0.05時，TMD最優阻尼比、頻率比、減振效果隨質量比的變化曲線。從圖4中可以看出：

（1）平穩白噪聲激勵下，無阻尼的主結構采用質量比大于0.04的最優參數TMD減振后，減震效果大于0，表明其變形幅值將小于阻尼比為5%的相應單自由度結構；

（2）復剛度阻尼TMD的減振效果略遜于黏滯阻尼，當質量比為0.05時，二者減振效果分別為9.9%和11%，減振效果相差1.2%。TMD應用于工程結構的風振控制時，質量比一般不超過0.05，從這個角度看，復剛度阻尼TMD看起來還是具有較好的應用前景；

（3）隨機過程激勵下，兩種阻尼對應的最優頻率比區別非常小，復剛度阻尼對應的最優頻率比稍大于黏滯阻尼。

圖4 平穩白噪聲風振作用下最優參數及減振效果隨質量比變化曲線Fig.4 Curves of optimization parameters and control effection change with mass ratio of structure with TMD disturbed by stationary white noise process excitation

6 達文波特風速譜作用下TMD減振結構的隨機響應分析算例

平穩白噪聲過程作用下結構的隨機響應的TMD減振效果不受結構頻率的影響，下面采用Davenport譜模擬脈動風速譜考察當主結構頻率變化時對TMD減振效果的影響。Davenport譜采用文獻［19］給出的形式：

式中：va10是10 m高處平均風速，本文算例中取13.89 m／s，常數c1取值600，κ時與地面狀況有關的參數，按文獻［19］中所列“市鎮”狀況取值0.03。在功率譜為Davenport譜的平穩隨機過程作用下主結構位移響應的功率譜和響應方差的計算公式為：

圖5 Davenport譜作用下主結構位移功率譜和減振效果Fig.5 Power spectrum and control affection ofmain structural displacement response of structure with TMD disturbed by stationary Davenport spectrum process excitation

圖5（a）圖給出的是復剛度阻尼和黏滯阻尼對應的TMD減振結構在主結構頻率ω0＝［2π／1，2π／4.5］時的主結構位移傳遞函數模的平方和功率譜，TMD的參數中質量比0.05，阻尼比和頻率比按表2中給出的最優參數取值。從圖5（a）中可以看出：

（1）Davenport譜放大了低頻區域的能量，主結構頻率值越大，低頻區域放大的程度越高。

（2）最優參數配置的復剛度阻尼和黏滯阻尼TMD結構中主結構的位移響應功率譜曲線在峰點處有一定差異，其他區域幾乎是重合的。

圖5（b）圖給出的是復剛度阻尼和黏滯阻尼對應的TMD減振結構的減振效果隨主結構頻率ω0的變化曲線，橫坐標從2π／5增加至2π／0.1，對應于周期從5 s減小到0.1 s。減振效果的定義同上節，即Davenport譜作用下TMD減振結構中主結構位移方差與相同條件下阻尼比為5%的單自由度結構方差響應的比值。從圖5（b）中可以看出：

（1）復剛度阻尼TMD減振效果稍遜于黏滯阻尼的情況，當ω0＝2π／5時，減振效果分別為4.6%和5.1%。當ω0＝2π／0.1時，二者對應值分別為0.81% 和0.73%，效果較為接近。

（2）TMD減振結構的減振效果隨著主結構頻率的增加而降低。即對于高頻結構，采用TMD的減振效果要明顯弱于長周期結構。

（3）Dawenport譜作用下TMD的減振效果要弱于白噪聲作用下的結果。

7 結 論

對復剛度阻尼在TMD減振體系中的應用進行了研究，推導了簡諧風振激勵下復剛度阻尼TMD的最優參數解析解，用數值擬合方法給出平穩白噪聲激勵下的優化參數公式，并對Dawenport譜作用下的主結構功率譜和方差響應進行了分析。得出如下結論：

（1）簡諧風振作用下采用復剛度阻尼的TMD減振結構的最優頻率比與采用黏滯阻尼時相同，在定點處的最大阻尼力和子結構振幅也一致。

（2）在簡諧激勵、平穩白噪聲隨機過程激勵以及平穩Dawenport譜隨機作用下，復剛度阻尼TMD的減振效果略小于黏滯阻尼，效果接近。

目前常規TMD大都采用線性黏滯阻尼，本文的研究工作初步表明復剛度阻尼在TMD結構風振控制方面可以取得與黏滯阻尼相近的效果，存在一定的應用價值。

［1］王肇民.電視塔結構TMD風振控制研究與設計［J］.建筑結構學報，1994（5）：2－13.

WANG Zhao-min.Study and design of TMD wind vibration control of TV tower structures［J］.Journal of Building Structures，1994（5）：2－13.

［2］歐進萍，王永富.設置TMD、TLD控制系統的高層建筑風振分析與設計方法［J］.地震工程與工程振動，1994（2）：63－77.

OU Jin-ping.WANG Yong-fu.Wind induced vibration analyses and design methods of tall buildings with tuned mass dampers of tuned liquid dampers［J］.Earthquake Engineering And Engineering Vibration，1994（2）：63－77.

［3］李春祥，熊學玉，胡俊生.TMD－高層鋼結構系統按規范抗風設計方法［J］.工業建筑，2000（4）：3－6.

LI Chun-xiang，XIONG Xue-yu，HU Jun-sheng.Windresistant design method for TMD-tall steel structure systems according to code provisions［J］.Industrial Construction，2000（4）：3－6.

［4］李春祥，劉艷霞.高層建筑TMD風振控制優化設計［J］.計算力學學報，2001（1）：71－75.

LIChun-xiang，LIU Yan-xia.Optimum design of TMD for suppressing vibration of tall building subjected to wind［J］.Chinese Journal of Computational Mechanics，2001（1）：71－75.

［5］背戶一登.動力吸振器及其應用［M］.北京：機械工業出版社，2013.

［6］Chung L L，Wu L Y，Huang H H，et al.Optimal design theories of tuned mass dampers with nonlinear viscous damping［J］.Earthquake Engineering and Engineering Vibration，2009，8（4）：547－560.

［7］Soong T T.結構工程中的被動消能系統［M］.北京：科學出版社，2005.

［8］Snowdon JC.Steady-state behavior of the dynamic absorber ［J］.Journal of the Acoustical Society of America，1959，31 （8）：1096－1103.

［9］丁文鏡.減振理論［M］.北京：清華大學出版社，1988.

［10］Inaudi J A，Kelly JM.Linear hysteretic damping and the hilbert transform［J］.Journal of Engineering Mechanics，1995，121（5）：626－632.

［11］Inaudi J A，Makris N.Time-domain analysis of linear hysteretic damping［J］.Earthquake Engineering and Structural Dynamics，1996，25（6）：529－545.

［12］Zhou Xi-yuan，Peng Ling-yun.A new type of damper with friction-variable characteristics［J］.Earthquake Engineering and Engineering Vibration，2010，8（4）：507－520.

［13］彭凌云，周錫元.擬線性摩擦阻尼器性能試驗與有限元分析［J］.建筑結構學報，2010（6）：194－200.

PENG Ling-yun，ZHOU Xi-yuan.Experiment and FEA on performance of pseudo-linear friction damper［J］.Journal of Building Structures，2010（6）：194－200.

［14］彭凌云，周錫元，閆維明.管式變摩擦阻尼器的減振性能試驗與數值模擬［J］.振動與沖擊，2012，31（5）：19－23.

PENG Ling-yun，ZHOU Xi-yuan，YANWei-ming.Test and numerical simulation for performance of a tubular type of variable friction damper［J］.Journalof Vibration and Shock，2012，31（5）：19－23.

［15］Penzien J，Clough R W.Dynamics of structures［M］.New York：McGraw-Hill，1993.

［16］Hahnkamm E，.Die d?mpfung von fundamentschwinggungen bei ver?nderlicher erregerfrequenz［J］.Ingenieur-Archiv，1932，4：192－201.

［17］Den Hartong J P.Mechanical vibrations［M］.New York：McGraw Hill，1956.

［18］方同.工程隨機振動［M］.北京：國防工業出版社，1995.

［19］歐進萍.結構隨機振動［M］.北京：國防工業出版社，1998.

Optimal design for structures including TMDsw ith com p lex stiffness and dam ping under w ind loads

PENG Ling-yun1，KANG Ying-jie1，QIN Li2，HE Hao-xiang1

（1.Beijing Municipal Key Lab of Earthquake Engineering and Structural Retrofit，Beijing University of Technology，Beijing 100124，China；2.School of Civil Engineering and Architecture，Hubei College of Arts and Science，Xiangyang 441053，China）

The study on the optimal design theory for vibration reduction structures with complex stiffness and damping is necessary.The dynamic equations for structures including tunedmass dampers（TMDs）with complex stiffness and damping were established.The method for determining their optimal frequency ratio and optimal damping ratio was presented based on the fixed point theory.The steady state responses of the such kind structures to harmonic excitation and stationary random excitation were analyzed，respectively.The theoretical formulas for the optimal damping and frequency were derived when the displacement amplitude minimization of the main structure was set as the optimal objective.The results showed that the overall vibration reduction effect of this kind of structures were close to that of structures with viscous damping，and the former is better in a certain frequency range with the same mass ratio.The random responses of this kind of structures under Davenportwind speed spectrum were analyzed.The results showed that the vibration reduction effect of TMDs with complex stiffness and damping is less than that under white noise excitation，the vibration reduction effect of the such kind structures is less than that of structures with viscous damping，but the difference is slight；so，if TMDs are applied in vibration control，adopting complex stiffness and damping is a profitable option.

complex stiffness and damping；TMD；steady state response；random vibration

TU352

A

10.13465／j.cnki.jvs.2015.21.005

國家自然科學基金資助（51008010）；國家自然科學基金資助（51208188）

2014－05－27 修改稿收到日期：2014－11－19

彭凌云男，博士，副研究員，1976年生