身管固有頻率高效全局靈敏度分析

陳光宋，錢林方，吉 磊

（南京理工大學機械工程學院，南京 210094）

身管固有頻率高效全局靈敏度分析

陳光宋，錢林方，吉 磊

（南京理工大學機械工程學院，南京 210094）

為獲得影響身管固有頻率的關鍵參數，將身管固有頻率寫成其參數的混沌多項式形式，提出基于靈敏度的混沌多項式自適應展開，采用LASSO（Least Absolute Shrinkage and Selection Operator）自動選擇重要項及其展開系數，根據混沌多項式的正交性直接由混沌多項式展開系數解析獲得身管參數的全局靈敏度因子。算例1表明基于靈敏度的多項式自適應展開能夠根據變量的重要性選擇多項式的展開階數，算例2通過一個標準模型驗證提出方法的有效性和高效性。此外，身管算例表明對于低階固有頻率搖架前支點位置及對應的身管圓柱段直徑和身管炮口處直徑為核心關鍵參數。

身管；靈敏度分析；混沌多項式；LASSO

身管為火炮的重要部件之一，其尺寸參數不僅要根據膛壓曲線變化規律由強度計算確定［1］，同時還要考慮其他因素，其中身管固有頻率即為一個重要的因素，獲取影響身管固有頻率的關鍵參數對身管的設計有重要意義。

靈敏度分析被應用于各個領域，如機械工程［2－3］，土木工程［4］，武器系統［5］，損傷診斷［6］等，其功能是量化輸入參數的不確定性對輸出的影響。通常，靈敏度分析可分為局部靈敏度分析和全局靈敏度分析，其中全局靈敏度分析研究的是參數在完整域內變化對系統輸出的影響［11］，大致可歸為三類：非參數技術［7－8］，方差分析法［9－10］和矩獨立重要性測度［11－12］。針對工程中的不同問題，國內外學者進行了研究和改進，例如李璐祎等［13］為分析參數區域的重要性，基于方差分析法，提出了基本變量區域重要性測度，并給出了相應的算法；張磊剛等［14］分析了高階核函數的性質，并將其應用到靈敏度分析中，能夠提高靈敏度分析的效率和精度；Ge等［15］針對大量輸入參數問題，將基于準優化軌跡的基本因素法和Sobol'靈敏度分析方法相結合，有效地解決多輸入參數情況下的全局靈敏度分析；Blatman等［16］采用混沌多項式展開，可直接解析地計算出Sobol'靈敏度因子等。

本文采用混沌多項式展開構建身管固有頻率與其參數的近似模型，根據多項式展開的稀疏性原理，提出基于靈敏度的混沌多項式自適應展開，并采用LASSO方法自動獲取重要項及其展開系數；基于Sobol'靈敏度分析方法［10］，根據混沌多項式的正交特性計算身管參數的全局靈敏度因子，獲得影響身管固有頻率的關鍵參數。

1 身管動力學方程

根據身管的結構及受力情況，將身管簡化為變截面Timoshenko梁。任意時刻t，梁上距局部坐標原點x處的橫向振動方程為［17］：

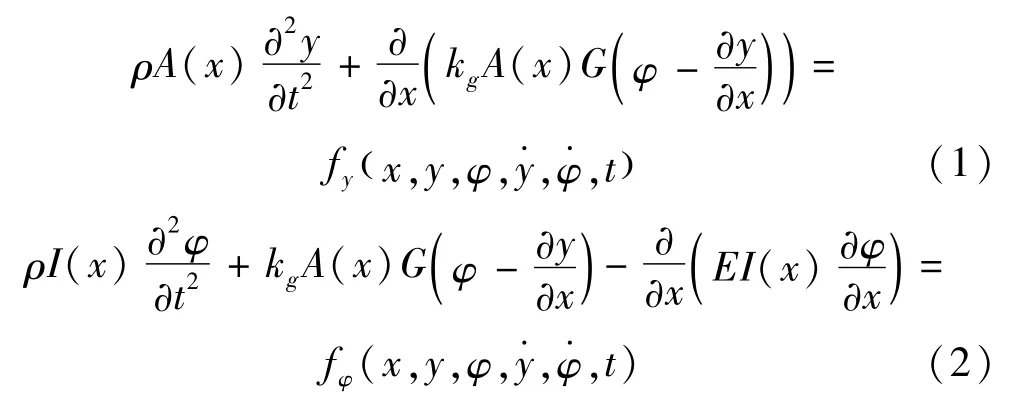
式中：L為梁長度，y和φ為梁的橫向位移和不考慮截面剪切位移的截面轉角，ρ為單位體積質量，A（x）為橫截面積，I（x）為橫截面慣量，kg為與截面形狀有關的剪切系數，G為剪切模量，E為彈性模量為橫向外載荷。

本文采用時間域上譜單元法進行解算，其具有譜方法的高精度、指數收斂和有限單元法的靈活性。與有限元法相似，譜單元法單元形函數可通過拉格朗日插值得到，即：

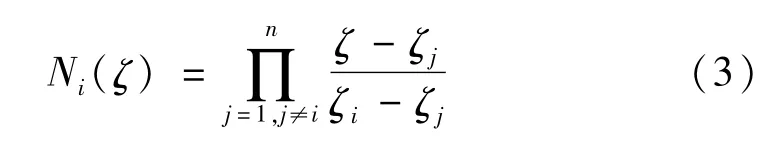
式中：插值點ζj不再沿插值方向均勻分布，而是以下等式的根，也稱為GLL（Gauss-Lobatto-Legendre）點分布：

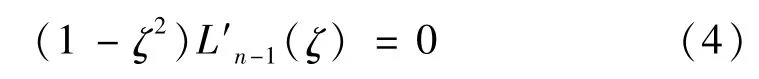
式中L′n－1（ζ）為n－1階Legendre正交多項式的一階導數。

譜單元法數值積分采用GLL積分方案，即積分點與GLL插值方案的插值點一致：

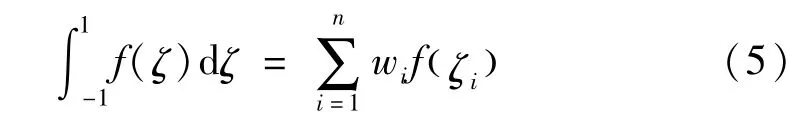
式中f（ζ）為被積函數，ζi為積分點，wi為權系數。

將插值函數式（3）代入到式（1）和式（2）可得運動方程的弱形式：

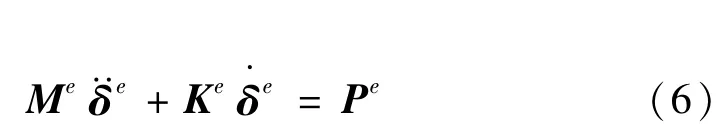
式中Me、Ke、δe、Pe分別稱為單元質量矩陣、剛度矩陣、節點位移列陣和載荷列陣。

獲得變截面Timoshenko梁單元矩陣后可使用與有限元相似的方法組裝成系統矩陣，假定身管被分割成N個單元，則系統剛度矩陣、質量矩陣、載荷列陣和位移列陣分別為：

式中為廣義特征值問題，解上式即可得到固有頻率ω和振型qΔ。

2 高效全局靈敏度分析

2.1 身管固有頻率自適應混沌多項式展開

混沌多項式展開近年來在不確定問題分析中逐漸得到應用。其基本思想是將系統的響應展開成有限的p階混沌多項式和的形式［18］。如圖1所示，考慮火炮身管、炮口制退器、炮尾的綜合模型，其中炮口制退器和炮尾簡化成集中質量。

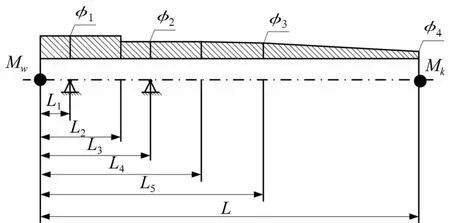
圖1 簡化身管模型Fig.1 Model of barrel

令x＝｛L1，L2，L3，L4，L5，φ1，φ2，φ3，φ4，Mw，Mk｝T為相互獨立的隨機變量，為方便表述，下文中用xj代表x中的第j個變量，f為身管的固有頻率，則f展開為x的混沌多項式形式為：

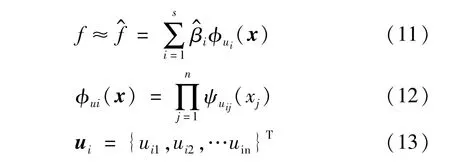
式中βi為多項式展開系數，s為展開項數，φui（x）為多元多項式，n為變量個數，ψuij（xj）是以xj的概率密度函數為權函數的混沌多項式，uij為多項式ψuij（xj）的階數，ui為各多項式階數的集合，滿足

式（11）中φui（x）包含了所有階數小于等于p的項，隨著輸入變量n和展開階數p的增加，s將呈指數增長。為實現模型的縮減，根據參數的重要性、主項和交叉項重要性的不同，假定STj為變量xj的全局靈敏度，定義：

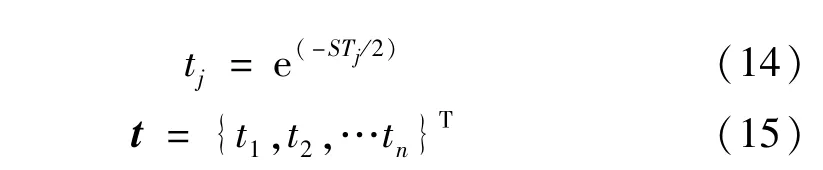
記tmin為t中的最小值，定義下式：

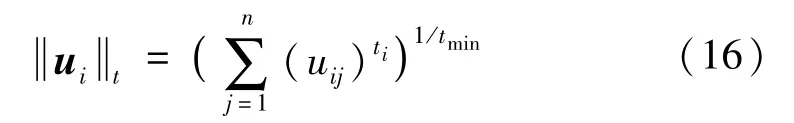
則滿足式（16）的混沌多項式展開集為：

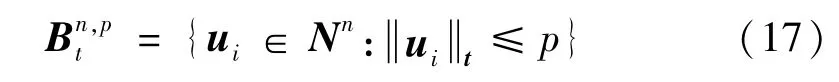
由式（14）可知，若系統對某個參數xj的靈敏度STj較大，則tj較小，進而由式（16）可得(uij)tj較小，因此含有xj的項就越容易被保留下來。

2.2 關鍵項的選擇及展開系數的計算

上節中通過基于靈敏度的混沌多項式自適應展開獲得了滿足稀疏性原理的混沌多項式展開集Bn，pt，由此可得：

為進一步降低試驗設計的規模，采用LASSO［19］方法同時識別重要的項并計算相應系數，定義為：

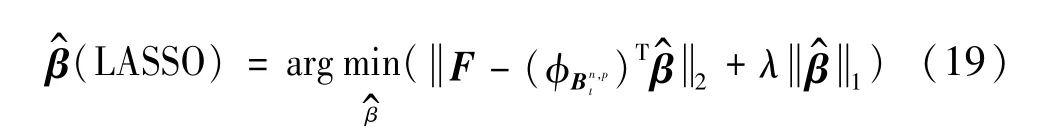
式中：F為輸出樣本，argmin（·）為對（·）求最小值，λ為調整參數。

采用最小角回歸（LAR）算法［20］解算式（19），并用相對留一誤差檢驗模型的精度：

2.3 基于混沌多項式展開的全局靈敏度

混沌多項式具有正交特性，即

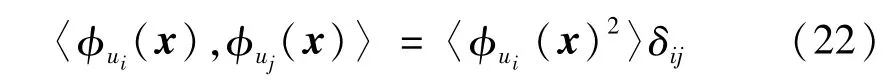
式中δij為克羅尼克符號。

由式（22）可很容易解析地求得f的期望μf和方差為：

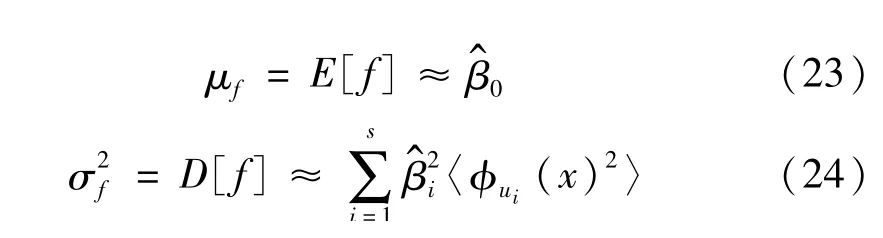
式中：E［·］表示求［·］均值，D［·］表示求［·］方差。

為計算參數的全局靈敏度因子，基于Sobol'靈敏度分析方法，可得混沌多項式展開中各項的靈敏度因子為：

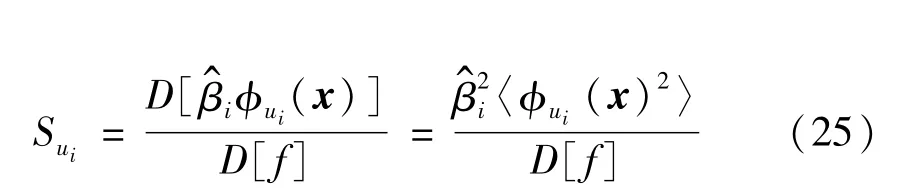
則考慮變量xk單獨作用的靈敏度Sk和總靈敏度STk分別為：

可見，獲得混沌多項式系數后，可直接解析地計算出全局靈敏度因子，與Monte Carlo相比可顯著提高計算效率，當獲得靈敏度因子后可用于更新自適應展開參數。計算流程如圖2所示。

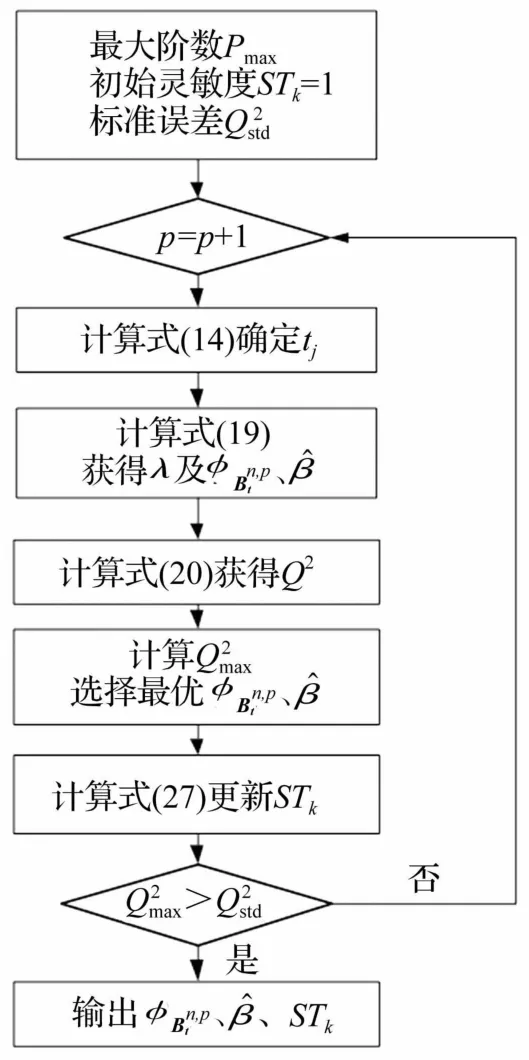
圖2 計算流程圖Fig.1 Flowchart of computation process

3 算 例

3.1 不同混沌多項式展開比較

取兩變量(x1，x2)模型，n＝2，p＝4，比較混沌多項式完備展開，雙曲展開［21］和自適應展開。其中雙曲展開方案中t＝0.9，自適應展開方案中ST1＝0.72，ST2＝0.3。不同方案的結果如圖3、圖4和圖5所示，圖中坐標軸表示變量的階數。由圖中可見完備多項式展開保留了所有小于p的項，雙曲多項式展開剔除了對稱高階交叉項，自適應多項式展開根據靈敏度分析結果剔除了不重要變量的高階項。

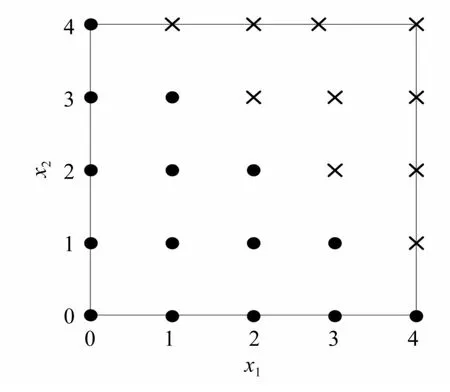
圖3 完備多項式展開Fig.3 Truncated by complete scheme

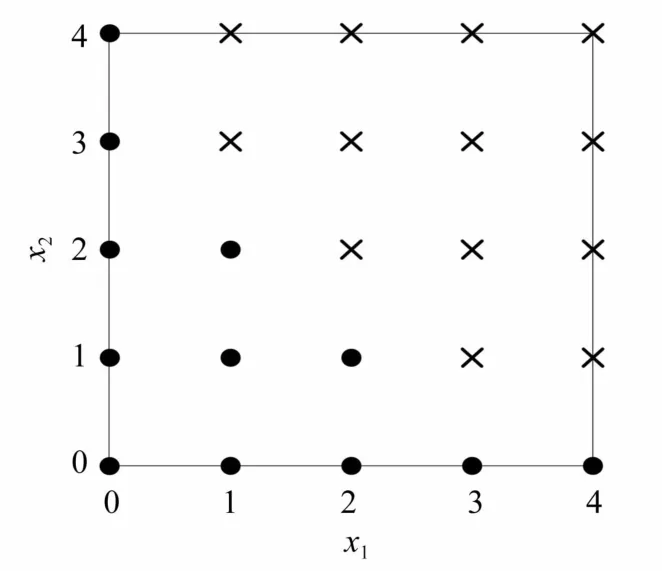
圖4 雙曲多項式展開Fig.4 Truncated by hyperbolic scheme

3.2 解析測試函數

Ishigami函數是靈敏度分析的基準函數［22］：

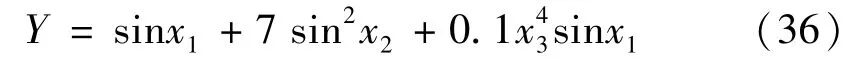
式中x1、x2、x3為相互獨立的隨機變量，在[－π，π]上滿足均勻分布。計算結果如表1所示，各參數的靈敏度因子結果如表2所示。結果顯示采用本文的方法可顯著減少試驗設計的次數，提高計算效率。靈敏度因子的相對誤差遠小于Crude MC方法，且不會出現靈敏度因子為負的現象。

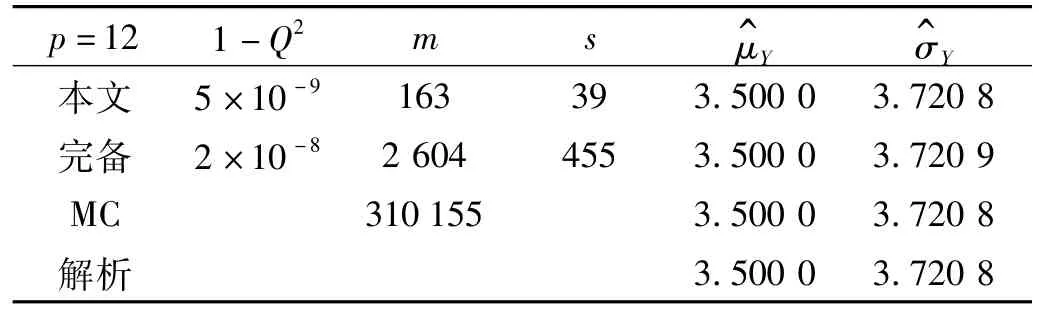
表1 Ishigam i函數的前2階統計矩Tab.1 Ishigam i function and the first two moments

表2 參數全局靈敏度分析Tab.2 Global sensitivity indices of parameters

圖5 自適應多項式展開Fig.5 Truncated by adaptive scheme

3.3 身管結構參數靈敏度分析

身管模型的基本參數為：E＝2.1×1011N／m2，G＝1／2.6E，kg＝9／10，ρ＝7 850 kg／m3。L1、L2、L3、L4、L5、φ1、φ2、φ3、φ4、Mw、Mp均服從高斯分布，其均值為現有身管的名義值，不確定參數如表3所示。混沌多項式的最大階數pmax＝7。前5階固有頻率如表4所示，圖6～圖10為輸入參數對各階固有頻率的靈敏度因子。

身管計算表明對于前五階固有頻率搖架前支點位置L3都是重要關鍵參數，除四階頻率外φ2對各階頻率都有重要影響，身管炮口處直徑φ4對一階頻率和三階頻率有重要影響，φ3對二階頻率和三階頻率較大影響，L1僅對四階頻率有較大影響，φ1對四階頻率有較大影響，對其余各階頻率影響較弱，L5對三階頻率有影響，L2、L4、Mw和Mk對前五階固有頻率均無影響。

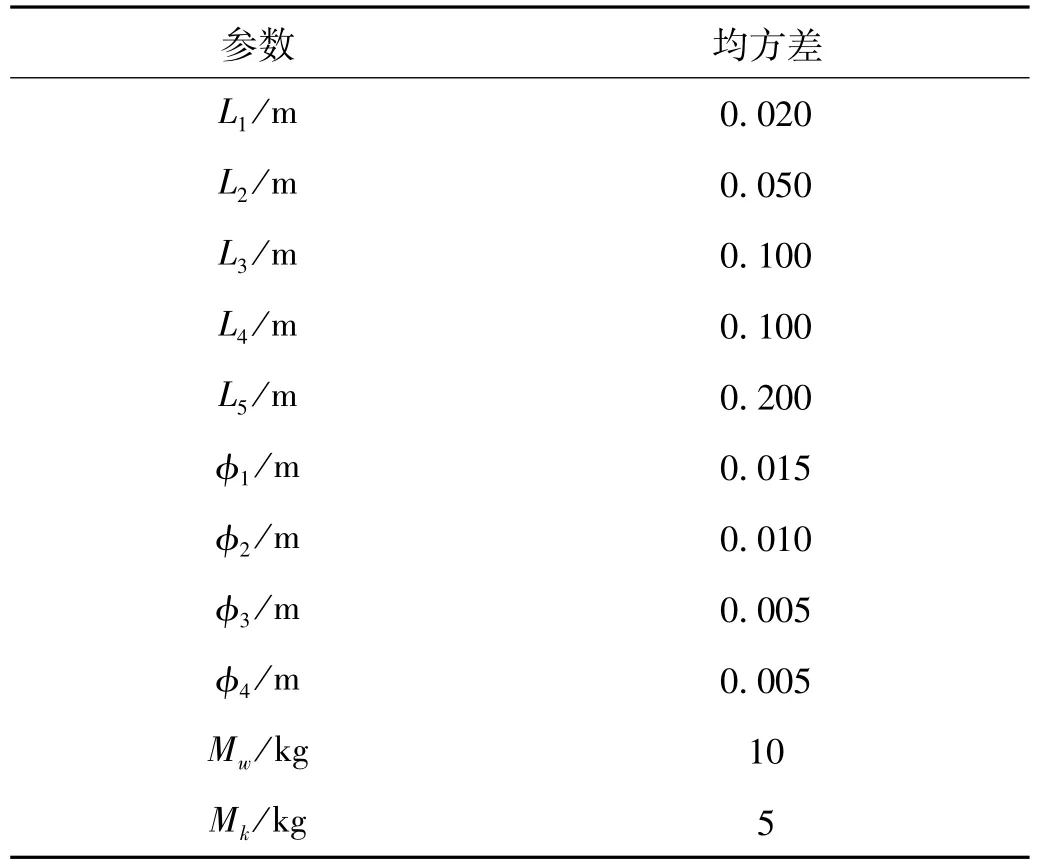
表3 輸入隨機參數Tab.3 Parameters of barrel

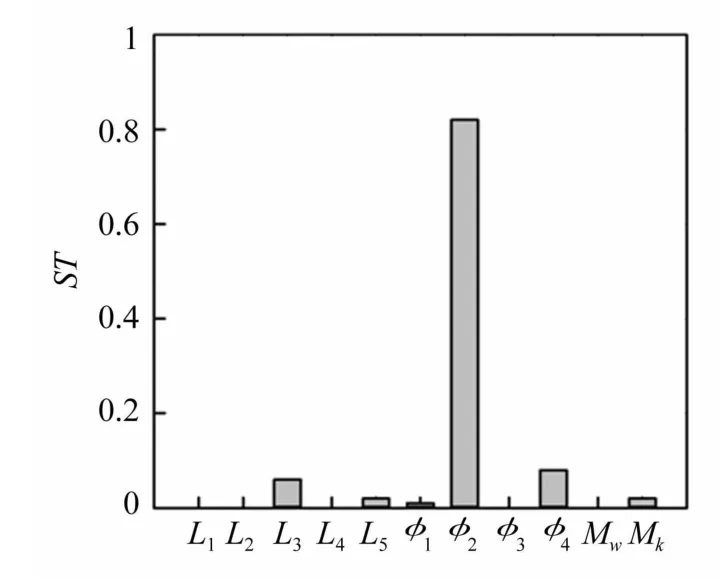
圖6 一階固有頻率各參數靈敏度Fig.6 Sensitivity indices of parameters for first frequency

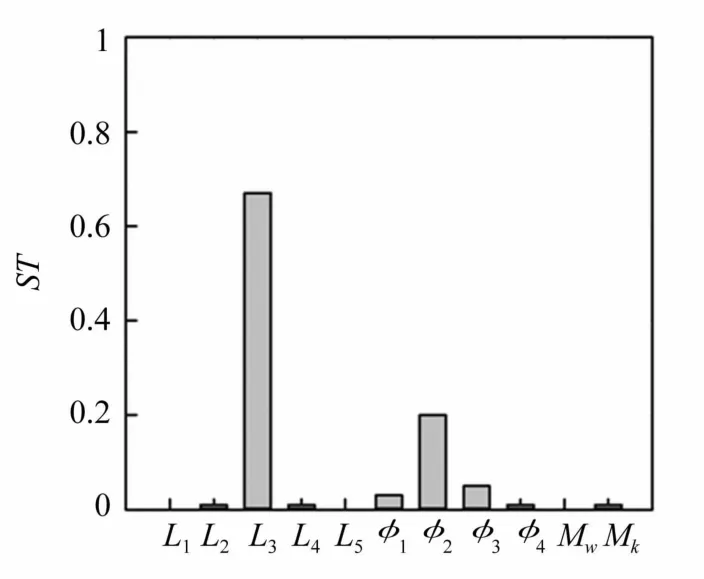
圖7 二階固有頻率各參數靈敏度Fig.7 Sensitivity indices of parameters for second frequency

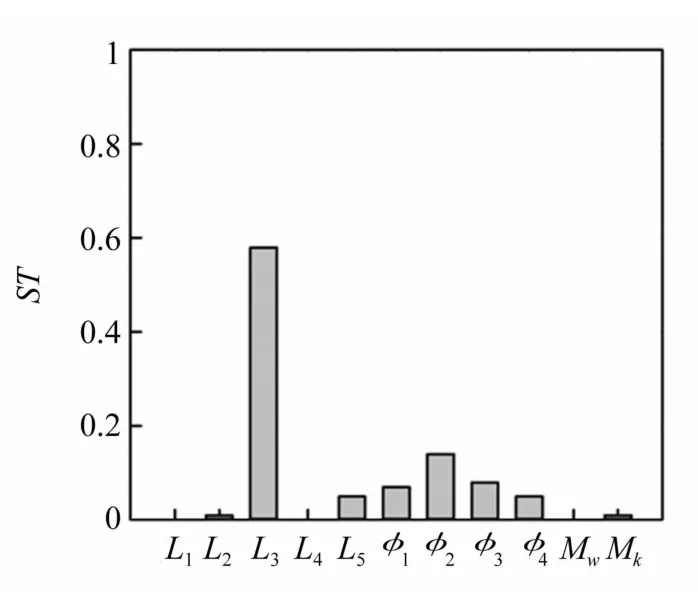
圖8 三階固有頻率各參數靈敏度Fig.8 Sensitivity indices of parameters for third frequency

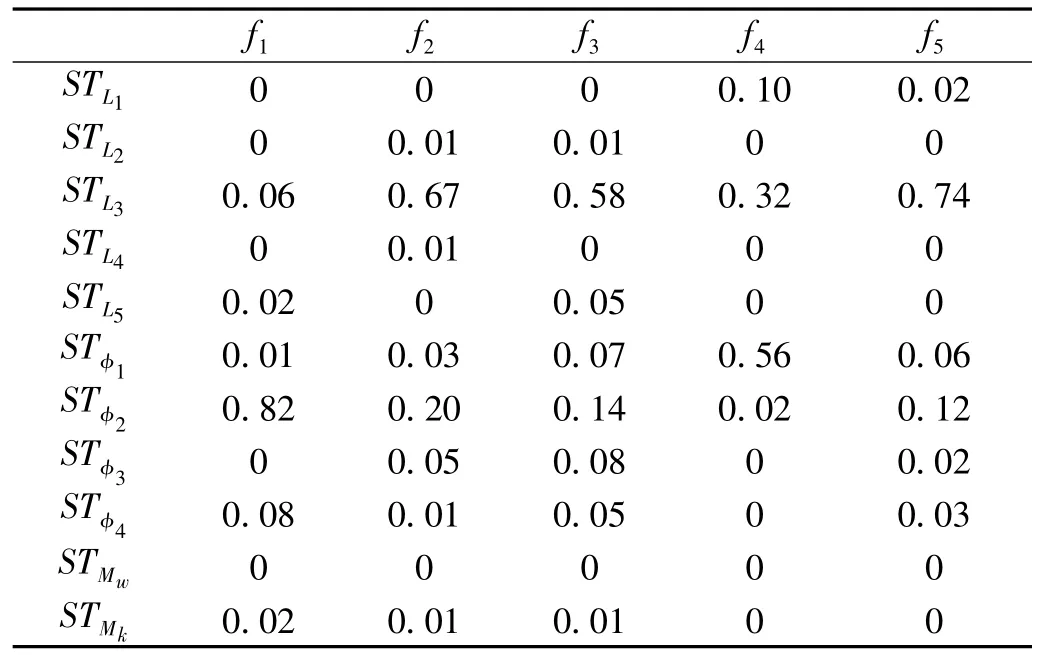
表4 前5階固有頻率Tab.4 First five frequencies

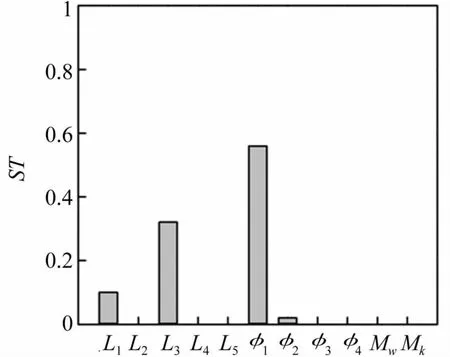
圖9 四階固有頻率各參數靈敏度Fig.9 Sensitivity indices of parameters for forth frequency

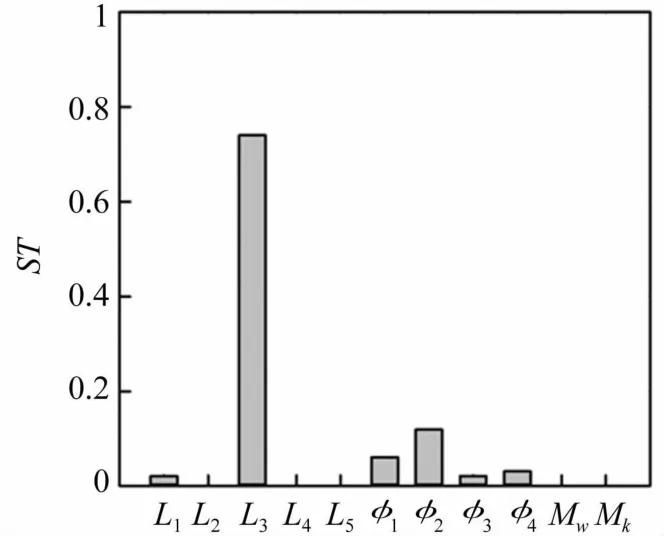
圖10 五階固有頻率各參數靈敏度Fig.10 Sensitivity indices of parameters for fifth frequency

4 結 論

本文將火炮身管固有頻率參數寫成其結構參數的混沌多項式形式，提出基于靈敏度的混沌多項自適應展開，并采用LASSO萃取出關鍵項保留在最終的模型中，通過基于混沌多項式的全局靈敏度分析獲得身管結構的關鍵參數，算例表明身管不同階固有頻率對應的關鍵參數不同，對于低階固有頻率搖架前支點位置L3及對應的身管圓柱段直徑φ2和身管炮口處直徑φ4為核心關鍵參數，算例結果可為火炮身管的優化設計提供依據。

［1］談樂斌，張相炎，管紅根，等.火炮概論［M］.北京：北京理工大學出版社，2005.

［2］黃毅，劉輝，項昌樂，等.車輛傳動系統非線性平移扭轉耦合振動響應靈敏度研究［J］.振動與沖擊，2014，33（23）：92－99.

HUANG Yi，LIU Hui，XIANG Chang-le，et al.Response sensitivity of nonlinear translation-torsional vibration coupled model of a vehicle transmission system［J］.Journal of Vibration and Shock，2014，33（23）：92－99.

［3］余衍然，李成，姚林泉，等.基于傅里葉幅值檢驗擴展法的軌道車輛垂向模型全局靈敏度分析［J］.振動與沖擊，2014，33（6）：77－81.

YU Yan-ran，LI Cheng，YAO Lin-quan，et al.Global sensitivity analysis on verticalmodel of railway vehicle based on extended Fourier amplitude sensitivity test［J］.Journal of Vibration and Shock，2014，33（6）：77－81.

［4］Hasofer A M.Modern sensitivity analysis of the CESARERisk computer fire model［J］.Fire Safety Journal，2009，44（3）：330－338.

［5］李皓川，孫志禮，王海.基于降維可視化技術的結構可靠性靈敏度分析［J］.兵工學報，2014，35（11）：1876－1882.

LI Hao-chuan，SUN Zhi-li，WANG Hai.Analysis of structural reliability sensitivity based on dimensionality reduction and visualization technique［J］.Acta Armamentar，2014，35（11）：1876－1882.

［6］傅奕臻，魏子天，呂中榮，等.基于時域響應靈敏度分析的板結構損傷識別［J］.振動與沖擊，2015，34（4）：117－120.

FU Yi-zhen，WEI Zi-tian，LüZhong-rong，et al.Damage identication of a plate based on response sensitivity analysis in time domain［J］.Journal of Vibration and Shock，2015，34（3）：117－120.

［7］Helton J C，Johson JD，Sallaberry C J，et al.Survey of sampling-based methods for uncertainty and sensitivity analysis［J］.Reliability Engineering＆System Safety，2006，91（10／11）：1175－1209.

［8］Saltelli A，Marivoet J.Non-parametric statistics in sensitivity analysis formodeloutput：a comparison of selected techniques ［J］.Reliability Engineering＆System Safety，1990，28 （2）：229－253.

［9］Iman R L，Hora S C.A robust measure of uncertainty importance for use in fault tree system analysis［J］.Risk Analysis，1990，10（3）：401－406.

［10］Sobol'I M.Global sensitivity indices for nonlinear mathematicalmodels and their Monte Carlo estimates［J］.Mathematics and Computers in Simulation，2001，55（1／2／3）：271－280.

［11］Borgonovo E.A new uncertainty importance measure［J］.Reliability Engineering＆System Safety，2007，92（6）：771－784.

［12］Liu H B，Chen W，Sudjianto A.Relative entropy based method for probabilistic sensitivity analysis in engineering design［J］.Journal of Mechanical Design，2006，128（2）：326－336.

［13］李璐祎，呂震宙.基本變量區域重要性測度及其稀疏網格解［J］.力學學報，2013，45（4）：569－579.

LILu-yi，LüZhen-zhou.Regional importancemeasure of the basic variable and its sparse grid solution［J］.Chinese Journal of Theoretical and Applied Mechanics，2013，45（4）：569－579.

［14］張磊剛，呂震宙，呂召燕，等.高階核函數的性質及其在靈敏度分析中的應用［J］.機械工程學報，2014，50（6）：27－32.

ZHANG Lei-gang，LüZhen-zhou，LüZhao-yan，etal.High order properties of kernel functions and their application in sensitivity analysis［J］.Journal of Mechanical Eengineering，2014，50（6）：27－32.

［15］Ge Q，Ciuffo B，Menendez M.Combining screening and metamodel-based methods：an efficient sequential approach for the sensitivity analysis of model outputs［J］.Reliability Engineering＆System Safety，2015，134：334－344.

［16］Blatman G，Sudret B.Efficient computation of global sensitivity indices using sparse polynomial chaos expansions ［J］.Reliability Engineering＆System Safety，2010，95（11）：1216－1229.

［17］Timoshenko S.Vibration Problem in Engineering［M］.New York：D.Van Nostrang Company，INC.，1937.

［18］Wiener N.The homogeneous chaos［J］.American Journal of Mathematics，1938，60：897－936.

［19］Tibshirani R.Regression shrinkage and selection via the Lasso［J］.Journal of the Royal Statistical Society：Series B （Methodological），1996，58（1）：267－288.

［20］Efron B，Hastie T，Johnstone I，et al.Least angle regression ［J］.The Annals of Statistics，2004，32（2）：407－499.

［21］Blatman G，Sudret B.Adaptive sparse polynomial chaos expansion based on least angle regression［J］.Journal of Computational Physics，2011，230（6）：2345－2367.

［22］Saltelli A，Chan K，Scott E M.Sensitivity Analysis［M］.New Jersey：Jhon Wildy and Sons，2000.

An effective global sensitivity analysismethod for natural frequencies of a barrel

CHEN Guang-song，QIAN Lin-fang，JILei

（School of Mechanical Engineering，Nanjing University of Science ang Technology，Nanjing 210094，China）

In order to obtain a barrel's key parameters affecting its natural frequencies，the polynomial chaos expansion was used to describe the relation of its natural frequencies and its structural parameters.The adaptive expansion strategy for the polynomial chaos based on the sensitivity was proposed to obtain polynomial chaos expansionswith different orders.The important terms and corresponding expansion coefficients were obtained automatically by using the least absolute shrinkage and selection operator（LASSO）.Based on the orthogonality of the polynomial chaos，the global sensitivity factors for structural parameters of the barrel were obtained directly with coefficients of the polynomial chaos expansion.Example 1 indicated that the proposed method can select expansion orders according to the importance of variables.A benchmark example was presented to demonstrate the effectiveness and higher efficiency of the proposed method.In addition，the numerical examples of barrels indicated that the position of the front fulcrum of the cradle，the corresponding cylinder diameters of barrels and the diameters at barrelsmuzzles are the key parameters affecting lower order natural frequencies of barrels.

barrel；sensitivity analysis；polynomial chaos；LASSO

TJ301

A

10.13465／j.cnki.jvs.2015.21.006

國家自然科學基金（11472137，51205207）

2015－02－02 修改稿收到日期：2015－04－14

陳光宋男，博士生，1987年生

錢林方男，教授，1961年生