基于近似慣性流形的非線性壁板熱氣動彈性響應降階方法

康 偉，唐 楊，徐 敏，張家忠

（1.西北工業大學航天學院，西安 710072；2.西安交通大學能源與動力工程學院，西安 710049）

基于近似慣性流形的非線性壁板熱氣動彈性響應降階方法

康 偉1，唐 楊1，徐 敏1，張家忠2

（1.西北工業大學航天學院，西安 710072；2.西安交通大學能源與動力工程學院，西安 710049）

基于近似慣性流形理論提出一種用于高溫環境下的二維壁板熱氣動彈性響應分析的降階方法。其主要思想是將壁板振動方程的解分解為高低階模態之和，并利用近似慣性流形理論建立高低階模態之間的耦合關系，用低階模態來表示高階模態的影響。通過與傳統的伽遼金法比較，結果表明所提方法可以在不明顯損失解的精度的前提下降低系統的自由度，提高計算效率。

非線性壁板；熱氣動彈性；近似慣性流形；降階模型

壁板熱氣動彈性響應是指壁板結構在高速氣流中，由于慣性力、彈性力、熱載荷以及作用于壁板表面上的氣動力之間耦合作用而產生的結構響應［1－2］。在超聲速和高超聲速飛行器高速飛行過程中，壁板熱氣動彈性振動［3－4］會減少壁板結構的疲勞壽命，甚至會給飛行器的飛行安全帶來不利的影響。

在研究壁板熱氣動彈性問題時，通常采用傳統伽遼金方法來求解壁板振動方程的解［5］。但是應用該方法得到的解的精度和計算效率往往得不到兼顧。理論上，只有待求函數選取無窮個模態時才能給出原方程的精確解。當待求函數的模態取得較少時，求得的解的精度達不到要求；當待求函數的模態取得較多時，數值模擬在運行過程中的運算量又會急劇增加，降低了計算效率，并造成誤差累積。根據近似慣性流形理論［6－7］，耗散動力系統的解的高低階分量間存在某種相互作用規律，即解的高階分量可由其低階分量表示出來。利用這個規律可以將原高維動力系統轉化成有限維動力系統而并不改變系統原來的拓撲性質。

本文在壁板氣動彈性耦合［8］的基礎上，考慮了高溫環境下壁板熱氣動彈性系統的降階問題。建立非線性壁板在高溫環境下的熱氣動彈性振動方程，并基于近似慣性流形理論，建立壁板熱氣動彈性系統高低階模態之間的耦合作用。使用該降階方法和傳統的伽遼金方法，對二維壁板動力系統響應進行了比較，來驗證所提降階方法的有效性與準確性。

1 非線性壁板熱氣動彈性力學模型

考慮展向無限長的各向同性平板，其中壁板上表面流過超音速氣流，且處于高溫環境中［9－10］，如圖1所示。

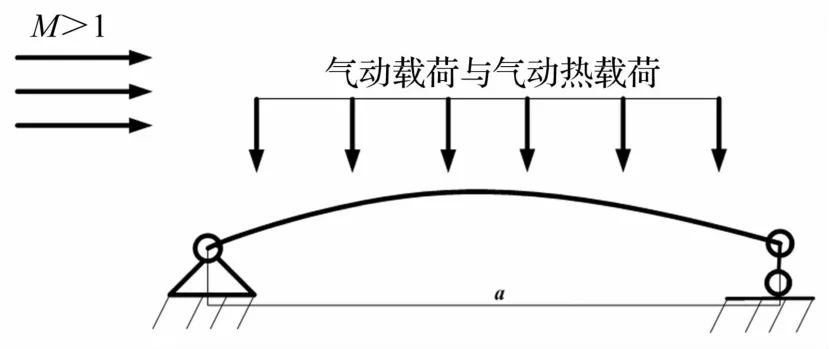
圖1 壁板熱氣動彈性力學模型Fig 1 Aero-thermo-elasticmodel of panel system

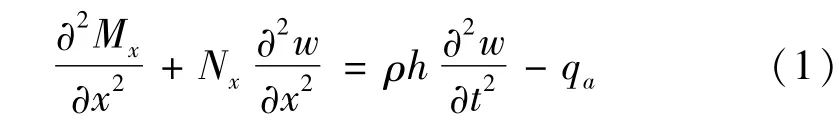
式中：w為壁板的橫向位移，Nx為面內載荷，Mx為彎矩，qa為氣動力。

由Von Karman大變形理論可得非線性應變－位移關系為

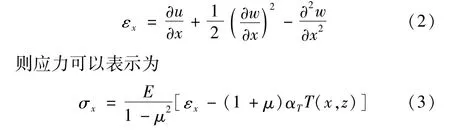
根據Kirchhoff理論，壁板振動方程為

式中：T（x，z）為壁板表面的溫度載荷，E，μ，αT分別為彈性模量，泊松比和熱膨脹系數。

基于準定常的熱應力公式，將溫度考慮為均勻的溫度場，即T（x，z）＝T。溫度升高引起壁板材料的機械性能發生改變，這里將E和αT表示為：

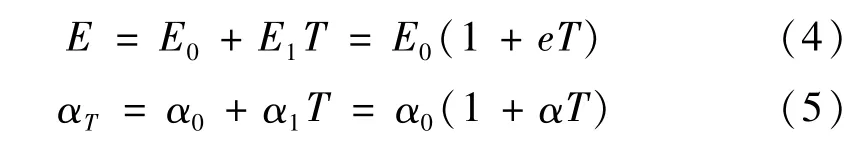
式中：E0，α0為加熱前材料的彈性模量和熱膨脹系數；E1，α1為溫度每升高一度材料的彈性模量和熱膨脹系數的變化量。e＝E1／E0，α＝α1／α0。一般來說，材料的彈性模量隨溫度升高而下降，而熱膨脹系數隨溫度升高而增大，因此有E1＜0，α1＞0。

則壁板所受載荷可以表示為

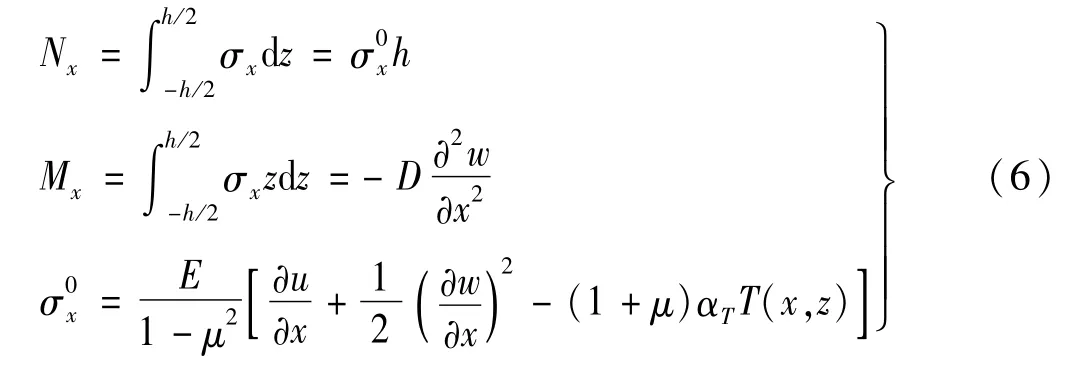
式中：ρ為壁板密度，h為壁板厚度，D＝Eh3／［12（1－μ2）］為彎曲剛度。

將式（6）代入式（1），可得壁板熱氣動彈性振動方程為

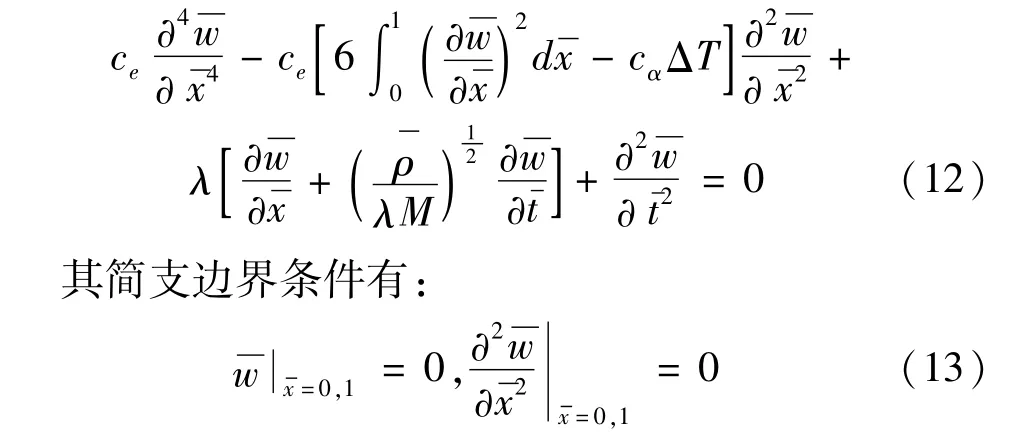
2 基于近似慣性流線的降階方法

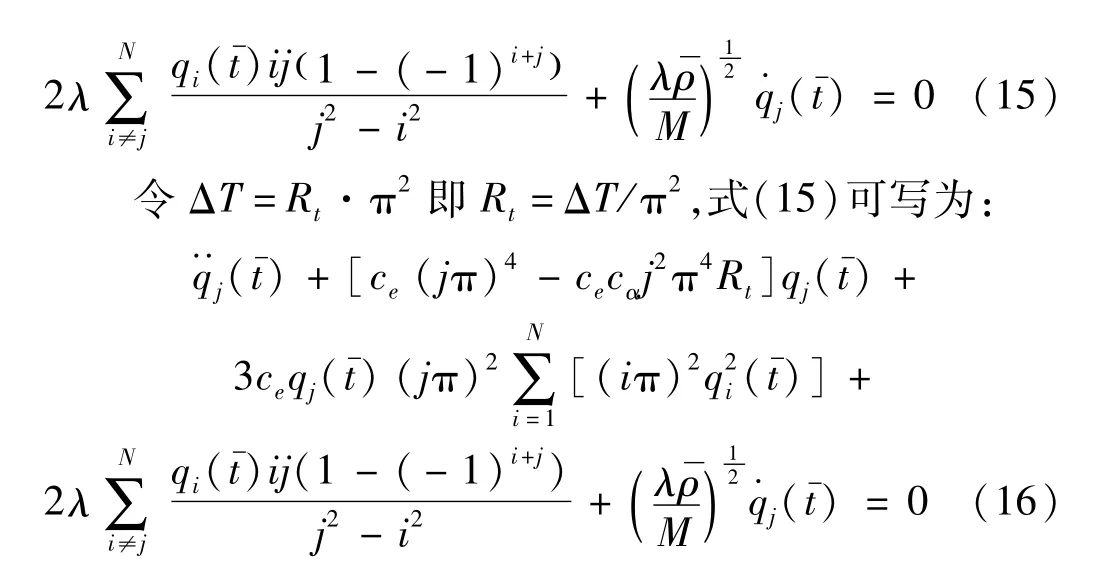
截取N個少量的模態（N＝2n，n為非零自然數）對壁板系統的動力學方程進行空間離散。視前n個分量為解的低階模態，后n個分量為解的高階模態。用Pn表示解空間的低階模態投影算子，記ln為解在Pn下的投影，有

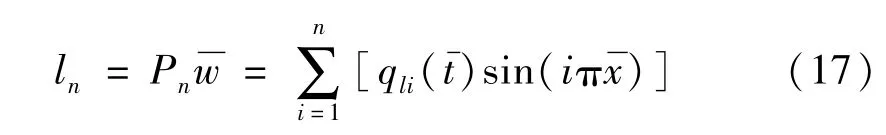
用Qn＝I－Pn表示解空間的高階模態投影算子，記hn為解在Qn下的投影，有

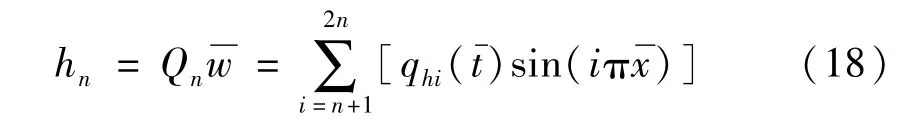
式（17）和（18）可將壁板的橫向位移表達為高低階模態之和的形式：

顯然，式（19）中如果只考慮低階模態的影響，即為傳統的伽遼金法。根據近似慣性流形理論［6，11］，在氣動阻尼作用下，壁板橫向位移的高階模態相對于低階模態會很快衰減掉，即高階模態所對應幅值的各階導數為零，則高階模態滿足：

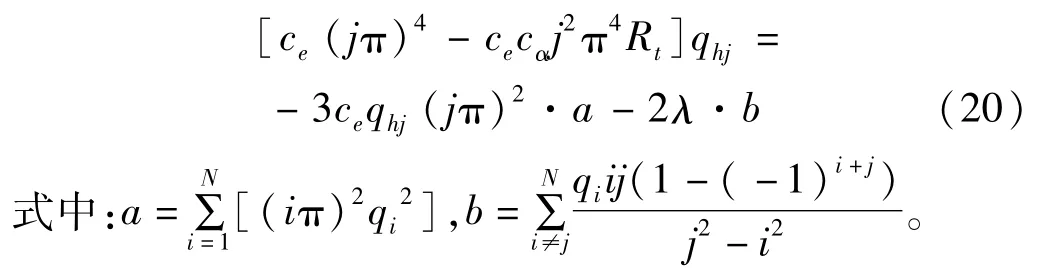
該式給出了高低階模態幅值間的相互關系。利用這個關系，就可以用低階模態幅值直接求得高階模態對應的幅值。由牛頓迭代法即可求得壁板橫向位移對應的高階模態系數。這樣在相同的模態數下，所提的降階方法避免了高自由度的數值積分過程的同時，保證了計算精度。

3 結果與分析

為了說明所提方法在壁板熱氣動彈性系統動力行為描述上的準確性，圖2給出了模態數為8時利用TGM方法和AIM方法得到的λ＝160時以Rt（溫差）為分岔參數的分岔圖。從圖中可以看到兩種方法所得的分岔點吻合良好，系統都經歷了穩定的平衡點、周期解（Hopf分岔）、倍周期分岔，最終進入混沌狀態。這說明文中所提的AIM方法能夠有效捕捉系統的非線性特征，準確描述系統的動力學行為。

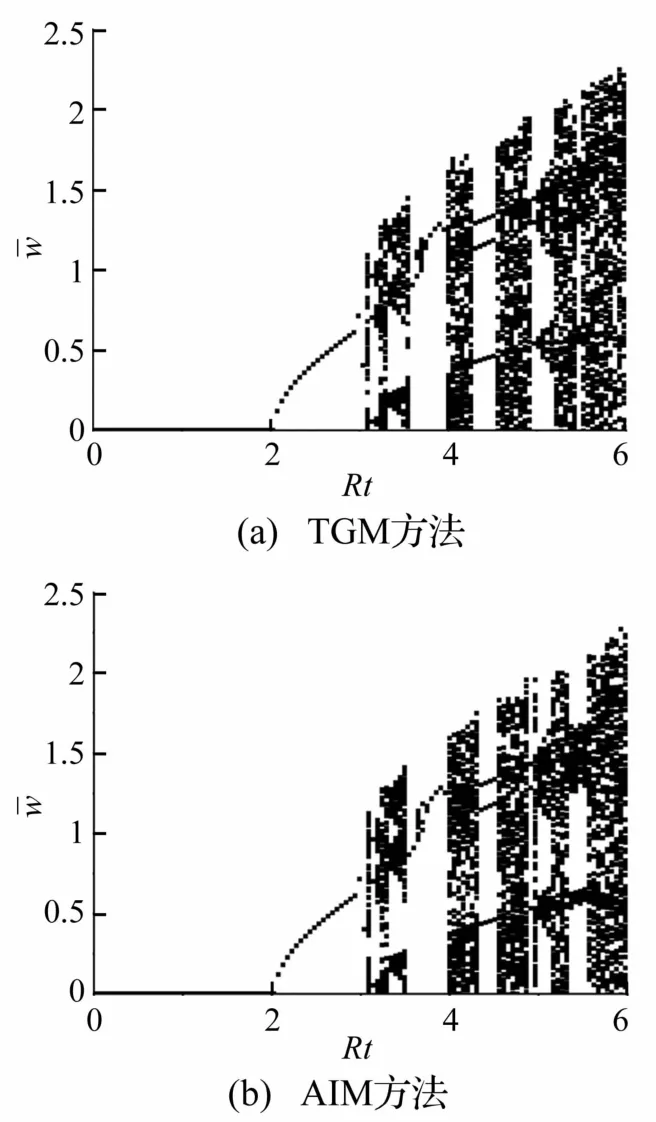
圖2 λ＝160時TGM方法和AIM方法得到的以Rt為分岔參數系統分岔圖Fig.2Bifurcationdiagramoftransversedisplacement ofpanelusingTGMandAIMmethodsforλ＝160（Rtisbifurcationparameter）

圖3給出了Rt＝2.53，λ＝50時不同模態數下x＝0.75處的壁板橫向位移的時間歷程。從圖中可以看出壁板歷經相似的衰減振蕩后，最終收斂到相同的穩定的平衡位置。系統從初始的平衡位置＝0.0最終將被吸引到新的平衡位置＝0.5890，這時系統發生了屈曲現象。對比圖3（a）和圖3（b）可以看到不同模態數時，TGM方法與AIM方法都吻合良好，這說明文中所提方法能夠達到傳統方法的精度，準確地描述系統的瞬態和穩態行為。表1給出了Rt＝2.53，λ＝50時兩種方法的CPU時間比較。當系統取較少模態數時，兩種方法的計算量相差并不明顯。AIM方法計算時間較TGM方法節省8.3250%。當系統模態數增加至16時，TGM方法耗時30.7188s，AIM方法相對TGM方法節省CPU計算時間9.0541%。

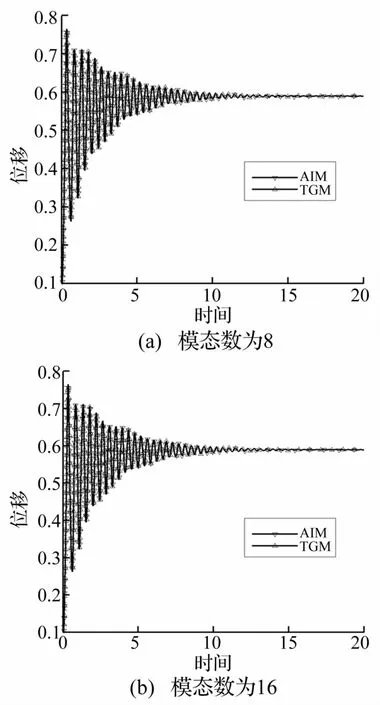
圖3 Rt＝2.53，λ＝50時壁板系統x＝0.75處橫向位移時間歷程Fig.3 Time history of transverse displacement of panelat x＝0.75 for Rt＝2.53，λ＝50

圖4給出了Rt＝3.0，λ＝200時不同模態數下x＝0.75處的壁板橫向位移的時間歷程。在Rt＝3.0，λ＝200時，系統的運動形式較圖3中所示的系統行為更為復雜。這時，系統的平衡位置發生失穩，系統變為極限環運動，即顫振。對比圖4（a）和圖4（b）可以看到選取不同模態數時，TGM方法與AIM方法在系統的瞬態與穩態行為描述上都吻合良好。這時從表1中可以看出模態數分別取8和16下AIM方法較TGM方法分別節省CPU時間26.133 6%，40.273 7%。這說明所提方法能夠在保證壁板熱氣動彈性方程解的精度的前提下有效降低系統的自由度。對于復雜的壁板熱氣動彈性動力學行為，AIM方法比TGM方法需要較少的計算時間，大幅提高計算效率。

比較壁板兩種響應下的計算時間可以看出不同形式的壁板運動形式下，AIM方法減少分析耗費的效果差別較大。這是由于AIM方法的主要思路是通過近似慣性流形所構造的映射（即建立高低階模態之間耦合作用關系），采用低階模態迭代計算得到高階模態的響應。對于壁板發生屈曲變形時，高階模態快速耗散，系統最終收斂到新的平衡位置。這時，高低階模態間的耦合相對較弱，采用近似慣性流形理論建立的迭代格式與直接數值積分（TGM方法）在計算效率上差別較小。當壁板發生顫振時，高階模態與低階模態發生耦合作用，采用近似慣性流形理論建立的迭代格式能夠更好地描述這種耦合關系，因此迭代求解高階模態響應的計算效率顯著高于直接積分方法。而且，當模態數越大時，這種計算效率上的差異越明顯。這說明了系統響應能夠反映高低階模態之間的耦合作用程度。當系統處于穩定的平衡位置時，高階模態逐漸耗散，高低階模態間的作用較弱。當系統處于周期運動時，高低階模態耦合變得強烈，高階模態參與到系統的響應中。

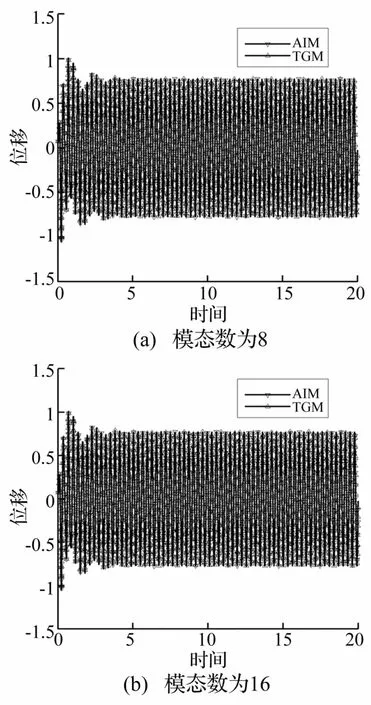
圖4 壁板系統x＝0.75處橫向位移時間歷程Fig.4 Time history of transverse displacementof panel at x＝0.75 for Rt＝3.0，λ＝200

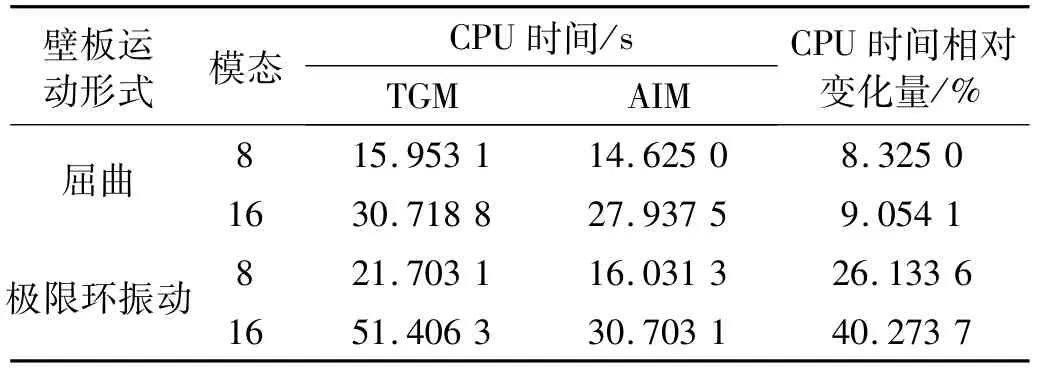
表1 不同情況下壁板熱氣動彈性動力系統的計算時間比較Tab.1 Com parison of CPU time for aero-thermo-elastic response of panel system

4 結 論

本文針對高溫環境下非線性壁板熱氣動彈性系統，基于近似慣性流形理論建立壁板熱氣動彈性系統的降階模型，并與傳統的伽遼金方法對二維壁板系統響應進行了比較。研究結果表明AIM方法在相同的模態數下能夠與TGM方法達到相同的計算精度，有效捕捉系統的非線性特征，準確描述系統的動力學行為。當系統發生屈曲時，AIM方法采用相同的16階模態數時，較TGM方法有效提高了計算效率，計算時間減少了9.054 1%；當系統發生復雜的周期運動時，AIM方法在相同的16階模態時較TGM方法節省CPU時間40.273 7%，表明AIM方法在不明顯損失解的精度的前提下降低了系統的自由度，大幅提高了計算效率。

［1］Dowell E.Panel flutter-A review of the aeroelastic stability of plates and shells［J］.AIAA Journal，1970，8（3）：385－399.

［2］Mei C，Abdel-Motagaly K，Chen R.Review of nonlinear panel flutter at supersonic and hypersonic speeds［J］.Applied Mechanics Reviews，1999，52（10）：321－332.

［3］Abbas LK，RuiX，Marzocca P，etal.A parametric study on supersonic／hypersonic flutter behavior of aero-thermo-elastic geometrically imperfect curved skin panel［J］.Acta Mechanica，2011，222（1／2）：41－57.

［4］Shore C，MeiC，Gray CE.A finite elementmethod for largeamplitude two-dimensional panel flutter at hypersonic speeds ［J］.AIAA Journal，1991，29（2）：290－298.

［5］肖艷平，楊翊仁，葉露.壁板邊界松馳下顫振非線性動力特性分析［J］.振動與沖擊，2014，33（3）：157－161.

XIAO Yan-ping，YANG Yi-ren，YE Lu.Nonlinear dynamic analysis for a panel's flutterwith boundary condition relaxation ［J］.Journal of Vibration and Shock，2014，33（3）：157－ 161.

［6］Temam R.Infinite dimensonal dynamical systems in mechanics and physics［M］.Berlin：Springer，1997.

［7］Kang W，Zhang J Z，Ren S，et al.Nonlinear Galerkin method for low-dimensionalmodeling of fluid dynamic system using POD modes［J］.Communications in Nonlinear Science and Numerical Simulation，2015，22（1／2／3）：943－952.

［8］梅冠華，張家忠，席光.基于時滯慣性流形的二維平面壁板非線性氣動彈性分析［J］.振動與沖擊，2012，31（10）：141－146.

MEI Guan-hua，ZHANG Jia-zhong，XI Guang.Nonlinear aeroelastic analysis of a two-dimensional panel based on inertialmanifolds with delay［J］.Journal of Vibration and Shock，2012，31（10）：141－146.

［9］楊智春，周建，谷迎松.超音速氣流中受熱曲壁板的非線性顫振特性［J］.力學學報，2012，44（1）：30－38.

YANG Zhi-chun，ZHOU Jian，GU Ying-song.Nonlinear thermal flutter of heated curved panels in supersonic air flow ［J］.Chinese Journal of Theoretical and Applied Mechanics，2012，44（1）：30－38.

［10］葉獻輝.壁板非線性氣動彈性顫振及穩定性研究［D］.成都：西南交通大學，2008.

［11］康偉，張家忠，李凱倫.利用本征正交分解的非線性Galerkin降維方法［J］.西安交通大學學報，2011，45 （11）：58－62.

KANG Wei，ZHANG Jia-zhong，LI Kai-lun.Nonlinear Galerkin method for dimension reduction using proper orthogonal decomposition［J］.Journal of Xi'an Jiaotong University，2011，45（11）：58－62.

Reduced order modeling for thermo-aero-elastic responses of a nonlinear panel in supersonic flow based on approximate inertialmanifolds

KANGWei1，TANG Yang1，XU Min1，ZHANG Jia-zhong2

（1.School of Astronautics，Northwestern Polytechnical University，Xi'an 710072，China；2.School of Energy and Power Engineering，Xi'an Jiaotong University，Xi'an 710049，China）

A method of reduced order modeling for thermo-aero-elastic response analysis of a nonlinear panel in supersonic flow was presented based on approximate inertialmanifolds.Itsmain idea was that the solution to the panel vibration equation was set as the sum of two groups including lowermodes and higher ones.The coupled relations between highermodes and lower oneswere established with the theory of the approximate inertialmanifolds，lowermodeswere used to express the effects of higher ones.Compared with the traditional Galerkin method，it was shown that the presented method can reduce DOFs of the system and improve computation efficiency without significant loss of the accuracy of the solution.

nonlinear panel；thermo-aero-elasticity；approximate inertialmanifolds；reduced ordermodels

O241

A

10.13465／j.cnki.jvs.2015.21.009

國家自然基金（11402212973）；國家重點基礎研究計劃（2012CB026002）；中央高校基本科研業務費專項資金資助（3102014JCQ01002）

2014－06－18 修改稿收到日期：2014－09－30

康偉男，博士，講師，1983年3月生