基于改進粒子群算法的Volterra模型參數辨識

衛曉娟，丁旺才，李寧洲，周學舟

（蘭州交通大學機電工程學院，蘭州 730070）

基于改進粒子群算法的Volterra模型參數辨識

衛曉娟，丁旺才，李寧洲，周學舟

（蘭州交通大學機電工程學院，蘭州 730070）

針對非線性系統Volterra泛函級數模型，結合混沌優化策略和種群多樣性控制思想，提出了一種改進粒子群算法，并應用于Volterra模型參數的辨識，將非線性系統的辨識問題轉化為高維參數空間上的優化問題。利用混沌序列增加初始種群的多樣性，通過構建動態子群以進行協作尋優，且各子群采用不同的參數自適應調整策略，并定義算法收斂性測度以對精英粒子進行合理的混沌變異，避免了算法早熟收斂，提高了算法的尋優速度和尋優精度。仿真實驗中，將該方法與基于標準粒子群算法、遺傳算法、量子粒子群算法的Volterra模型參數辨識方法相比較，驗證了該辨識方法的有效性和魯棒性。

改進粒子群算法；非線性系統；Volterra級數；系統辨識

Volterra級數模型由意大利科學家Volterra提出，它能完全刻畫系統非線性傳遞特性［1］，因此Volterra級數可以描述一大類非線性現象。對于該模型參數辨識的研究是利用Volterra級數模型描述并研究非線性系統動態特性、并由此監測和評估非線性系統健康狀況的關鍵。

非線性系統Volterra核的辨識實質上是一個優化問題。目前Volterra模型的辨識方法有傳統的最小二乘算法［2－5］、遺傳算法［6－7］、蟻群算法［8］、量子粒子群算法［9－10］等，但是，最小二乘算法辨識時要求目標函數連續可導，且采用梯度信息進行搜索，容易陷入局部最小，而遺傳算法等智能計算方法雖然克服了傳統辨識算法的相應缺點，但在算法結構和優化效率上依然有改進的余地。

粒子群算法（Particle Swarm Optimization，PSO）是基于生物種群模擬的群體智能優化算法［11－12］，具有結構簡單、易于實現等特點［13］。因此，本文把粒子群算法引入到非線性Volterra級數模型的辨識中，且為了提高算法性能和避免陷入局部極值點，提出了一種改進粒子群算法（Improved Particle Swarm Optimization Algo-rithm，IPSO）。IPSO算法在初始化階段以混沌序列初始化種群，增加了初始搜索的遍歷性，進化過程中則依據粒子性能將粒子群劃分為不同子群，且各子群采用不同的參數自適應調整策略，同時定義了算法收斂性測度以便采用混沌變異策略對部分粒子進行合理變異，不僅增加了種群的多樣性、避免了算法陷入局部最優，而且實現了全局探索和局部開發能力的平衡，提高了算法的整體尋優效率。將IPSO算法應用于一個典型的Volterra級數模型并進行仿真實驗，驗證了本文提出的辨識方法的有效性和魯棒性。

1 改進粒子群算法

1.1 標準粒子群算法

標準粒子群算法（Standard Particle Swarm Optimization，SPSO）的核心思想是通過跟蹤粒子當前的局部最優解和全局最優解來更新粒子速度和位置，達到中止條件時，當前全局最優解即作為優化問題的最優解。

假設粒子群規模為n，粒子j的速度和位置分別用M維向量Vj和Xj表示，則SPSO算法的進化方程為［14］

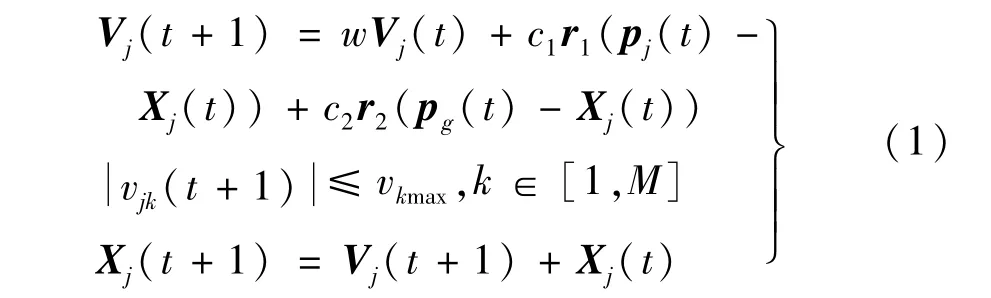
式中，Vj（t）為粒子j在第t代的速度，Xj（t）為粒子j在第t代的位置，Pj（t）為粒子j在第t代的個體歷史最優位置，Pg（t）為粒子群在第t代的歷史最優位置，w為慣性權重，c1為認知系數，c2為社會系數，r1、r2為各分量在［0，1］之間的M維隨機向量。Pj（t）和Pg（t）的更新規則為［14］

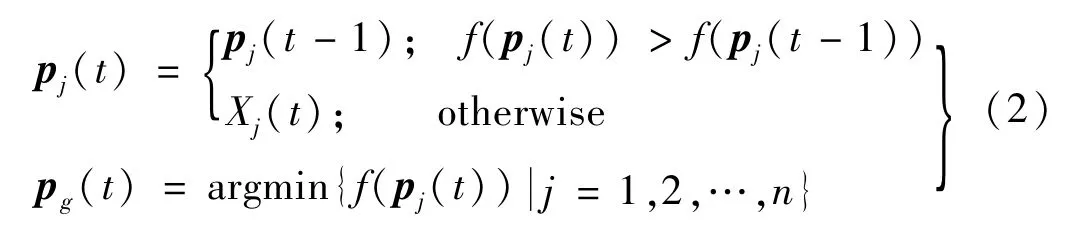
式中，f（Pj（t））表示Pj（t）的適應值，對于最小化問題而言，適應值越小，對應的適應度越優；argmin ｛f（Pj（t））｜j＝1，2，…，n｝表示使f（Pj（t））取最小值的Pj（t），該Pj（t）則作為第t代群體最優位置Pg（t）。

1.2 改進粒子群算法的改進策略

目前大多數文獻并未考慮按照粒子的性能進行參數調整［17－19］，從而在一定程度上影響了算法的尋優效率；同時，搜索過程中由于粒子群的聚集性，群體多樣性的丟失不可避免，可能陷入局部極值而造成早熟收斂。

基于此，本文提出的IPSO算法的改進策略主要體現在三個方面：①粒子群的混沌序列初始化；②根據粒子性能，在進化過程中動態構建精英子群和普通子群，并對各子群采用不同的參數自適應調整策略，以增加種群多樣性、同時實現全局探索和局部開發能力的平衡；③對部分精英粒子進行混沌變異操作。

1.2.1 粒子群的混沌序列初始化

采用混沌序列初始化粒子群，是在不改變PSO算法初始化時所具有的隨機性本質的前提下，利用混沌思想提高種群的多樣性和粒子搜索的遍歷性。文獻［14－16］通過分析指出式（3）所示Tent模型比Logisitic映射具有更好的遍歷性和更高的搜索效率，并驗證了Tent模型在增加種群多樣性及改善算法尋優性能方面的有效性。

假設粒子群規模為n，變量的維數為M維。粒子群初始化時，首先隨機產生一個M維，且每個分量數值在［0，1］之間的向量T1＝（T11，T12，…，T1M），然后將其代入式（3），經過N次（N＞n）迭代產生一個包含N個向量T1，T2，…，Tm，…，TN的混沌序列，再將Tm（m＝1，2，…，N）的各個分量經映射xmk＝xkmin+（xkmaxxkmin）Tmk（k＝1，2，…，M）轉化到對應變量的取值區間，構成包含N個初始粒子的群體，再通過比較這N個粒子的適應值，從中選出適應值相對較小的n個解作為初始解，此即為粒子群的初始位置。

1.2.2 參數自適應調整策略

（1）子群構建

設X（t）＝｛X1（t），X2（t），…，Xn（t）｝為第t代的群體，f（Xj（t））為Xj（t）的適應值，f（Xj（t））越小，粒子適應度越優（即其性能越優）；為了依據粒子性能構建子群，定義群體平均適應度為

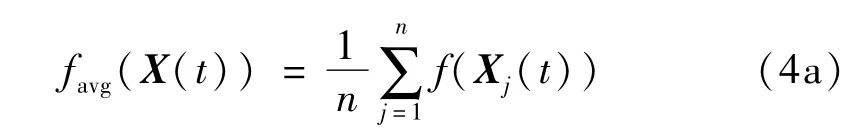
定義群體最優適應度為

定義優秀子群為

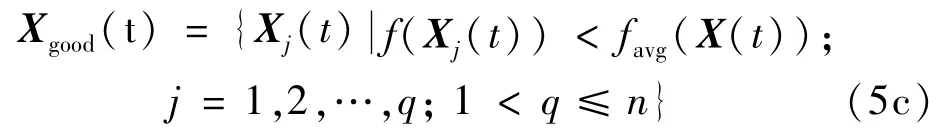
式中，q為優秀粒子數。

定義優秀粒子平均適應度為

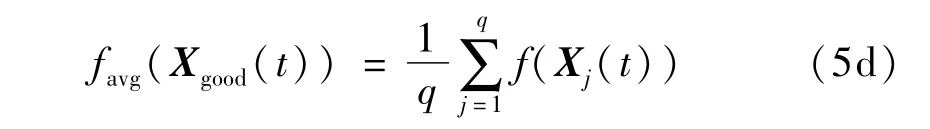
則可構建精英子群和普通子群如下：

定義1精英子群 精英子群定義為

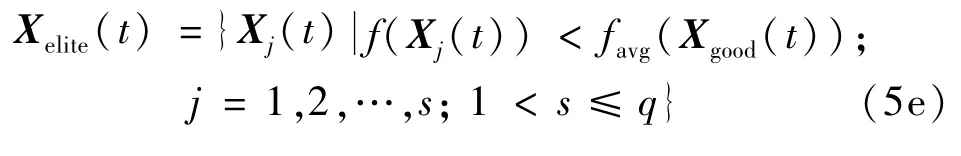
式中，s為精英粒子數。

定義2普通子群 普通子群定義為

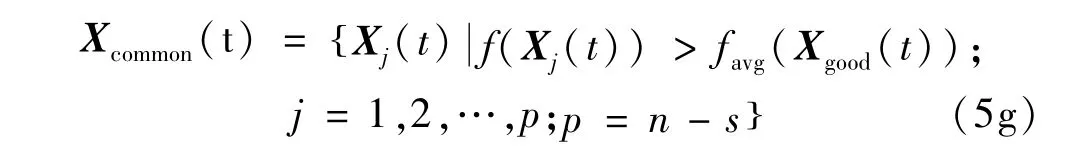
式中，p為普通粒子數。

（2）慣性權重的自適應調整策略

①精英子群慣性權重調整策略

設wj（t）為粒子j在第t代的慣性權重。為了說明IPSO中精英子群的wj（t）調整策略，引入下列定義：

定義3 精英子群最差適應度 精英子群最差適應度定義為

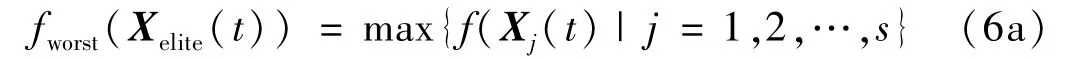
定義4 精英粒子性能指標 精英粒子性能指標定義為

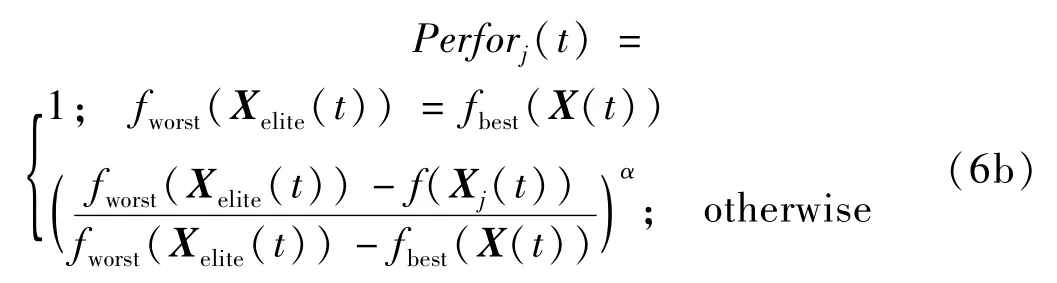
式中，Perforj（t）∈［0，1］。精英粒子j在第t代的適應度越優，Perforj（t）越大，反之，則越小；α的取值根據實際問題確定。

將Perforj（t）作為精英粒子j在第t代對慣性權重的影響因子，則精英粒子j在第t代的慣性權重為

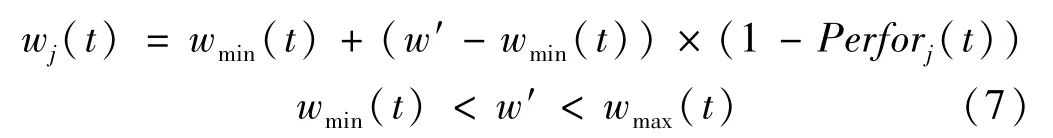
式（7）表明，Perforj（t）越大的精英粒子，全局最優出現在其周圍的概率越大，而較小的慣性權重能增強算法的局部開發能力，所以wj（t）應較小，以便保證這類粒子進行局部搜索；反之，Perforj（t）越小，全局最優出現在其周圍的概率越小，因較大的慣性權重能增強算法的全局探索能力，所以wj（t）應較大，以便保證這類粒子進行全局搜索。

②普通子群慣性權重調整策略

IPSO算法中，普通子群按照式（8）調節wj（t）。

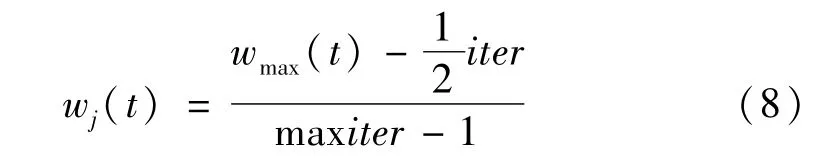
式中，iter為迭代步數，max iter為最大迭代步數。此時，wj（t）隨迭代進行按線性規律遞減。

（3）c1、c2的自適應調整策略

c1和c2的調整會影響到算法的收斂性能和收斂速度。因此，IPSO算法中，采用式（9）對c1、c2進行迭代更新。

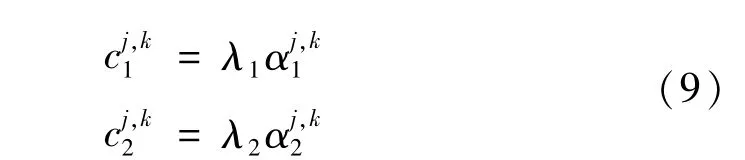
式中，j，k表示粒子j的第k維，λ1，λ2為收縮因子，λ1、 λ2∈（0，3），α1、α2為［0，1］之間的隨機數。

按式（9）調整c1、c2時，對于優秀子群，因其比較接近全局最優，所以c1應較小、c2應較大，以加速收斂到全局最優，從而提高算法的尋優效率和尋優精度；而對于普通子群，因其具有良好的全局探索能力，所以應使c1較大、c2較小，以擴大算法的搜索范圍，防止陷入局部最優。

1.2.3 混沌變異策略

（1）算法收斂性測度

為了定量描述粒子群的狀態，避免盲目變異引起的大量運算以及對算法收斂速度的影響，采用粒子群平均點距作為算法收斂性測度來衡量算法的收斂情況，以便合理進行變異操作以擴大搜索空間。

定義5 粒子群平均點距 設群體的平均中心為

（2）混沌變異策略

對粒子速度進行變異以使粒子在相應進化代數條件下對搜索空間進行大范圍的遍歷，當算法陷入局部最優時，使之能夠跳出局部極值點，進入解空間的其它區域繼續搜索。

根據式（3）所示Tent模型迭代產生一個包含若干個向量T1，T2，…的混沌序列，再將Tk的各分量經過映射變換至原粒子速度的解空間，得到若干個向量V1，V2，…，以此替代精英子群中按比例選取的精英粒子的速度，即得到變異后該部分粒子的當前速度。

2 非線性系統Volterra模型辨識

2.1 Volterra模型描述

對于具有輸入x（k）和輸出y（k）的離散時間非線性動態系統，可用Volterra級數將其描述為［9］：

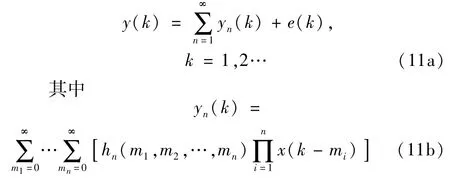
式中，e（k）為截斷誤差。hn（m1，m2，…，mn）為非線性系統的n階Volterra時域核，又稱為廣義脈沖響應函數（GIRF）。GIRF具有對稱性，且對稱性是唯一的［1］。利用Volterra核的對稱性，可以大大減小利用Volterra級數模型描述非線性系統所需參數的數目，從而可大大減小計算量。

利用前三階Volterra級數模型即可近似描述很多的實際非線性系統，因此，非線性系統Volterra模型的辨識通常是對其Volterra級數模型的一階、二階和三階核進行辨識［1］。

考慮GIRF的對稱性，根據式（11），則系統輸出可表述為：

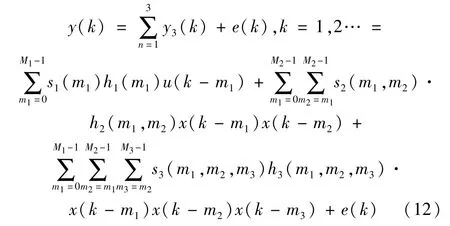
式中，Mi為記憶長度；Mi取適當值時，e（k）可充分小，在誤差允許范圍內，e（k）可忽略不計；s1（m1）、s2（m1，m2）、s3（m1，m2，m3）由式（13）確定。

若假設截斷Volterra級數模型的最高階次為N，定義系統的輸入矩陣為：

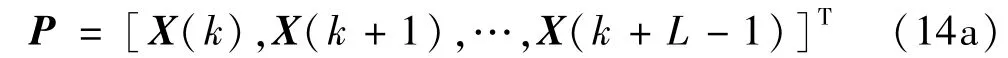
式中，L為數據長度。則k時刻的輸入（列）向量X（k）可定義為：

式中，e為誤差。

由式（15）可知，基于截斷Volterra級數模型的非線性系統辨識，就是在已知系統的輸入、輸出序列｛x（k）｝、｛y（k）｝的基礎上求解核向量H。其辨識實質上是一個最優參數估計問題。

假設粒子群規模為n，將Volterra模型的待估計參數（核矢量H）作為IPSO算法中的粒子位置，則粒子j的位置用M維向量表示，粒子群的位置可以用矩陣表示。對粒子j而言，算法中控制辨識誤差的適應度函數定義為

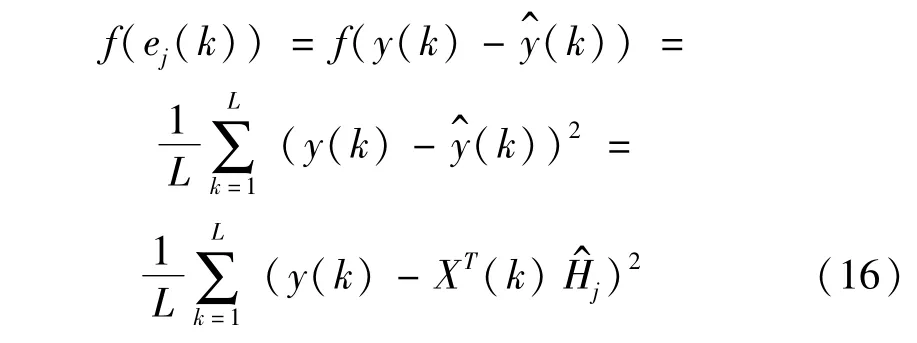
式中，L為數據長度，j＝1，2，…，n。

通過搜索使適應度函數值（即適應值）最小的全局最優解Pg，即是Volterra核矢量H的最優解H＾。

2.2 Volterra模型辨識流程

利用IPSO算法對形如式（15）所示有限階非線性離散系統的Volterra模型參數進行辨識的算法流程如圖1所示。

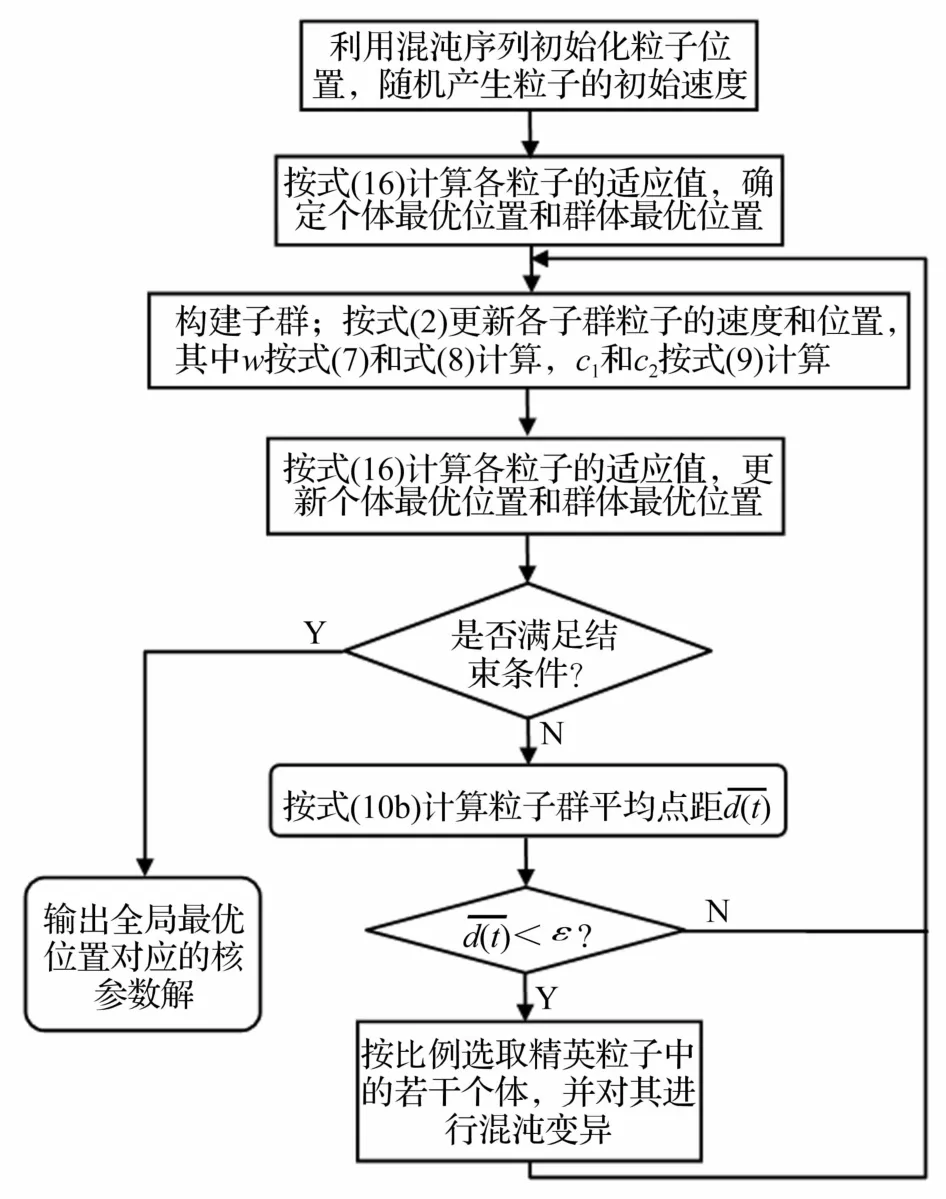
圖1 基于IPSO的Volterra模型辨識算法流程圖Fig.1 The identification algorithm of Volterra kernel based on the IPSO

3 Volterra模型辨識測試

作為辨識目標的Volterra模型如式（17）所示。

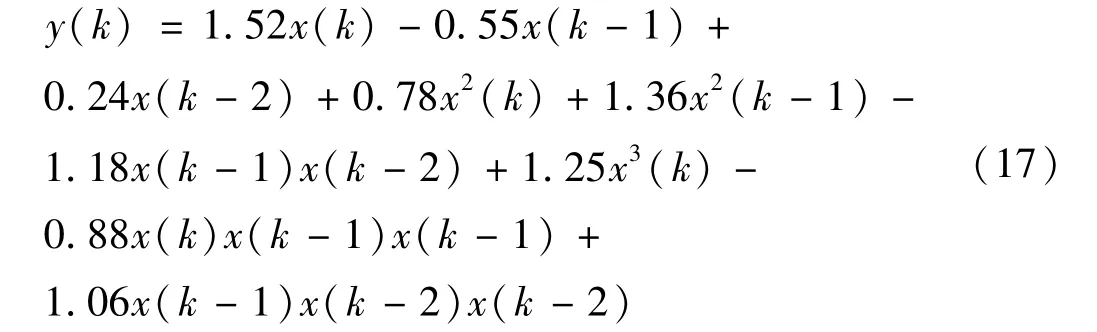
式（17）所示模型的一階、二階和三階核的記憶長度均為3，核向量為：H＝［1.52，－0.55，0.24，0.78，0，0，1.36，－1.18，0，1.25，0，0，－0.88，0，0，0，0，1.06，0］T。

利用本文提出的IPSO算法對式（17）所示三階非線性系統的Volterra模型進行辨識，系統的輸入信號為［0，1］之間的均勻白噪聲信號，種群規模為80，維數為19，最大進化代數為800，系統辨識的對比測試重復進行20次，結果取運行20次結果的平均值。

表1為無噪聲情況下，IPSO算法、SPSO算法、遺傳算法（簡稱GA算法）、量子粒子群算法（簡稱QPSO算法）所得到的Volterra模型參數的估計值。

為了考察存在噪聲干擾時本文算法的辨識精度和抗噪性能，在輸入、輸出端疊加獨立平穩的白噪聲，且輸入輸出信號的信噪比均為20 dB［9］。表2為四種算法測試得到的辨識結果。

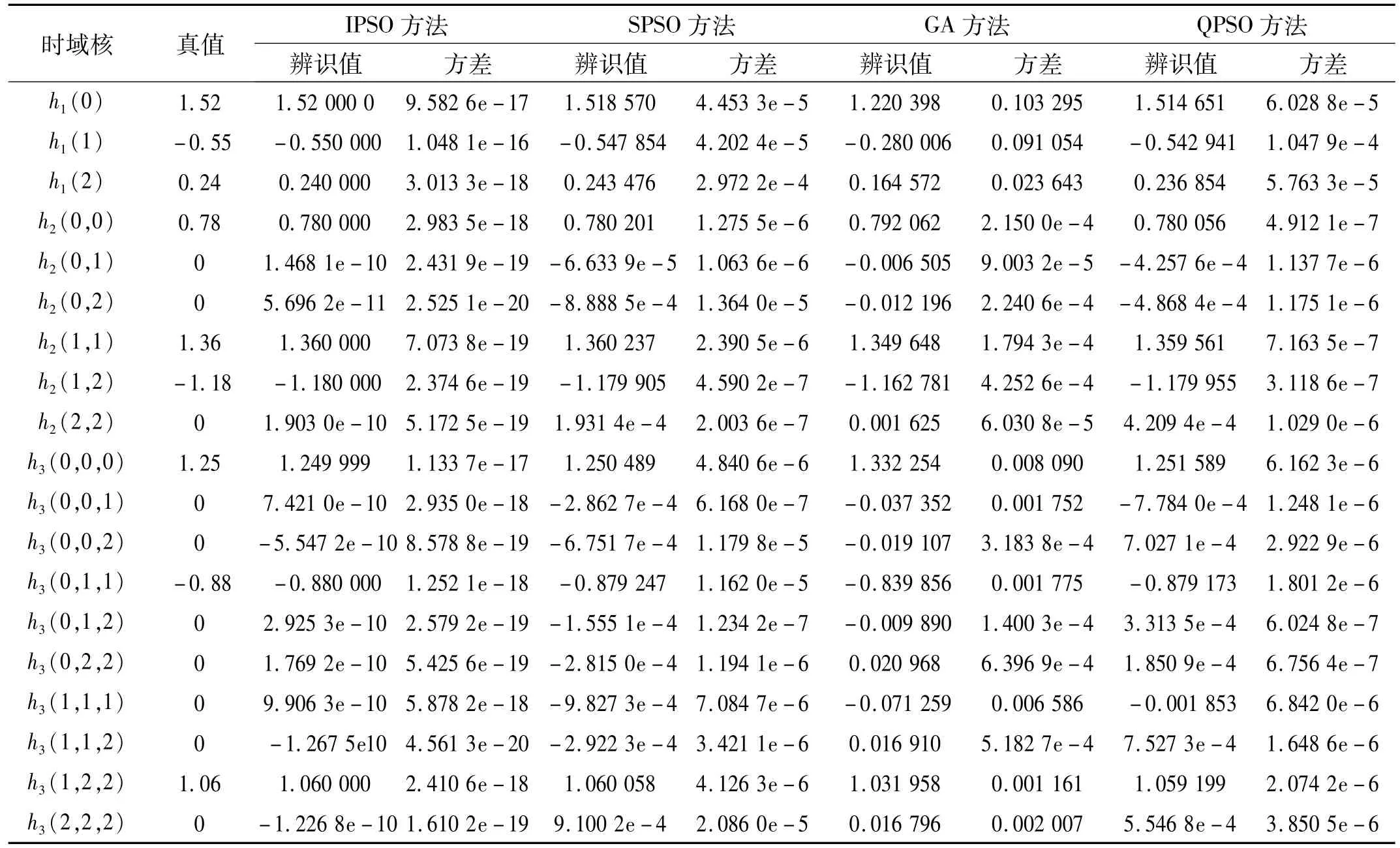
表1 無噪聲干擾下Volterra模型辨識結果Tab.1 Estimation results of the Volterra model under the free－noise environment

由表1可知，在無噪聲干擾情況下，四種算法均可得到真值的近似值，說明四種算法均可用于Volterra模型參數的辨識。其中應用IPSO算法得到的估計值的平均值更加接近真實值，其辨識精度明顯較高。

由表2亦可看到，在加入噪聲干擾時，IPSO算法得到的估計值的誤差相對較小，顯然噪聲干擾并未對其辨識精度產生影響，體現了IPSO算法具有較強的魯棒抗噪性能。

圖2給出了無噪聲情況下，四種辨識方法分別得到的一階時域核參數h1（1）、二階時域核參數h2（1，2）和三階時域核參數h3（1，2，2）的進化曲線；圖3給出了無噪聲情況下，四種辨識方法的平均適應度值變化曲線。

從圖中可以看出，IPSO算法的收斂速度明顯快于其他三種算法，雖然其他三種算法最終也能較為準確地估計出Volterra核參數的值，但是收斂速度相對較慢；且由圖3可看出，IPSO算法相較SPSO算法而言，其全局探索能力和局部開發能力都得到了改善，在整個進化過程中IPSO算法表現出了較強的持續尋優能力，未陷入局部最優，且辨識精度明顯優于其他三種算法。

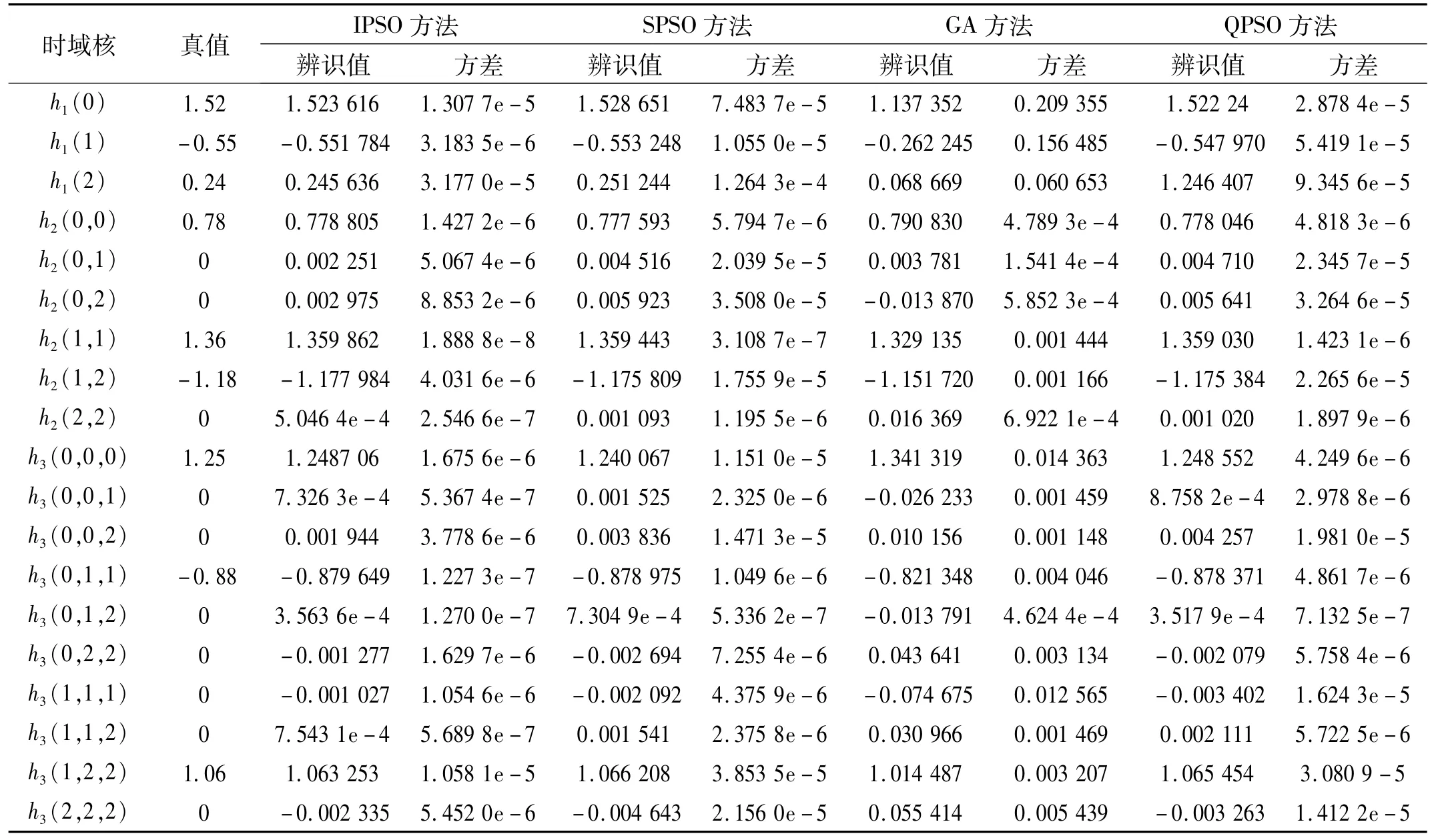
表2 信噪比20 dB時Volterra模型辨識結果Tab.2 Estimation results of the Volterra m odel（SNR＝20 dB）

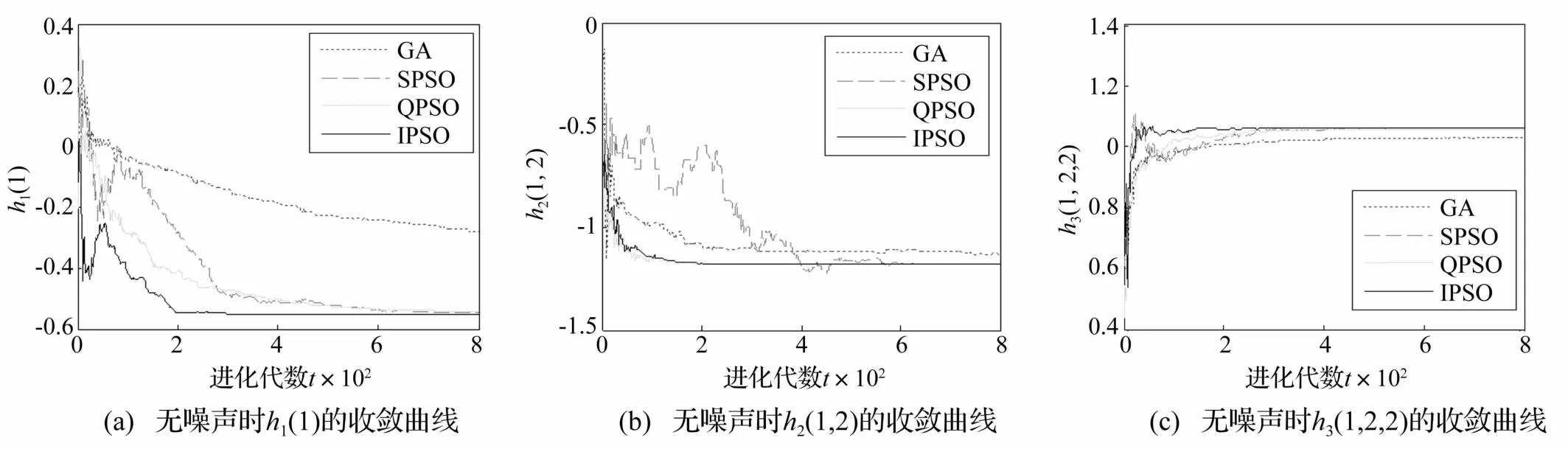
圖2 無噪聲時h1（1），h2（1，2），h3（1，2，2）的收斂曲線Fig.2 The evolution curves of the Volterra kernel vector h1（1），h2（1，2），h3（1，2，2）under the free-noise environment

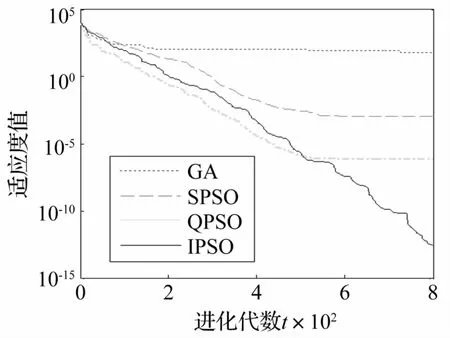
圖3 無噪聲時適應度函數變化曲線Fig.3 The curves of the fitness function under the free-noise environment

圖4給出了信噪比20 dB情況下，四種辨識方法分別得到的一階時域核參數h1（1）、二階時域核參數h2（1，2）和三階時域核參數h3（1，2，2）的進化曲線。從圖可以看出，IPSO算法的收斂速度明顯快于其他算法，雖然其他算法最終也能較為準確地估計出Volterra核參數的值，但是由于噪聲干擾，收斂速度相對較慢，尤其是SPSO算法的收斂過程波動也較大。

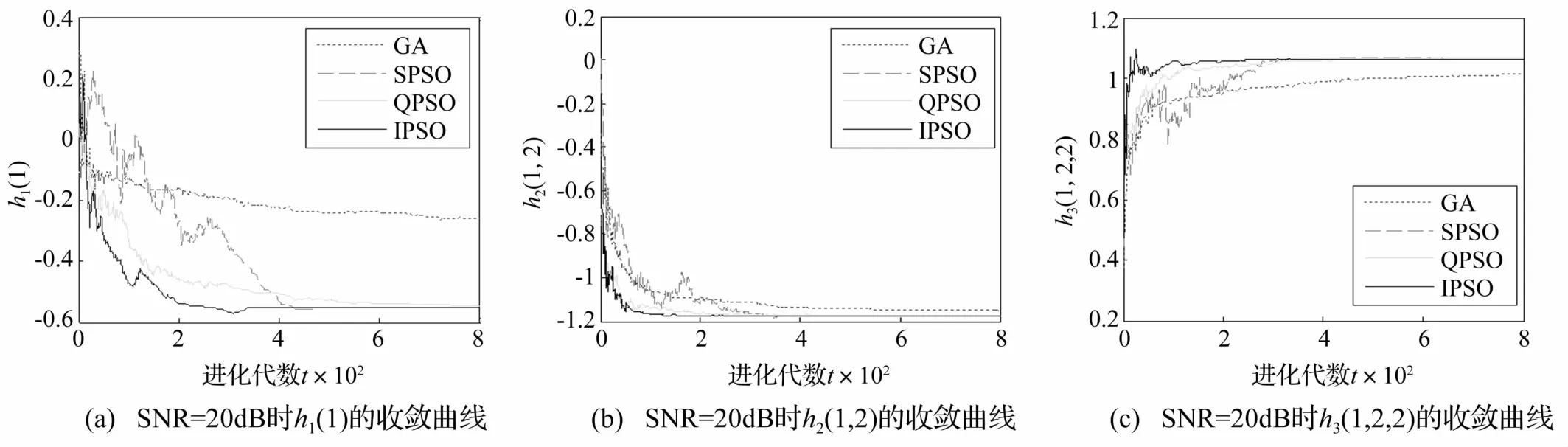
圖4 SNR＝20 dB時h1（1），h2（1，2），h3（1，2，2）的收斂曲線Fig.4 The evolution curves of the Volterra kernel vector h1（1），h2（1，2），h3（1，2，2）（SNR＝20 dB）

綜上所述，IPSO算法的尋優性能和效率明顯優于SPSO算法和GA算法，且相對于QPSO算法其性能也有一定提高。這主要是因為IPSO算法是在SPSO算法的基礎上經過優化而來。參數的自適應調整加快了算法的計算效率，組合混沌策略的引入有效避免了SPSO算法局部收斂與早熟的問題，而SPSO算法早期收斂速度較快，但到尋優后期其收斂速度則比較緩慢，這主要是因為算法收斂到局部極小時缺乏有效機制使算法逃離極小點，從而導致算法在接近或進入最優點區域時的收斂速度比較緩慢。因此，相對而言，本文提出的方法在全局優化能力和快速收斂能力上都有較大的提高，很好地克服了基于SPSO算法的Volterra模型辨識方法的不足。

4 結 論

本文將改進粒子群算法（IPSO算法）引入到非線性系統Volterra模型參數的辨識中，并在仿真研究中，將該辨識方法與相應的基于SPSO算法、GA算法和QPSO算法的辨識方法進行了對比分析。結果表明，即使在有噪聲干擾的情況下，提出的方法也能得到很好的參數辨識精度，且收斂過程依然平穩，表現出很好的魯棒抗噪性能。與其他三種算法相比，由于本文提出的方法將種群劃分為不同的子群，且不同子群采用相應的參數自適應調整策略，并利用混沌變異算子對一定比例的精英個體進行變異操作，所以既增加了種群多樣性、又很好地利用了不同粒子分別進行全局探索和局部開發，提高了算法的計算效率。本文提出的IPSO算法及其在非線性系統Volterra模型辨識中的應用研究為非線性系統辨識提供了一種新的有效方法，具有重要的理論價值和實際應用價值。

［1］曹建福，韓崇昭，方洋旺.非線性系統理論及應用［M］.西安：西安交通大學出版社，2006.

［2］張家良，曹建福，高峰.大型裝備傳動系統非線性頻譜特征提取與故障診斷［J］.控制與決策，2012，27（1）：135 －138.

ZHANG Jia-liang，CAO Jian-fu，GAO Feng.Feature extraction and fault diagnosis of large-scale equipment transmission system based on nonlinear frequency spectrum ［J］.Control and Decision，2012，27（1）：135－138.

［3］張華君.基于遞推批量最小二乘的Volterra級數辨識方法［J］.小型微型計算機，2004，25（12）：2282－2285.

ZHANG Hua-jun.Volterra series identif icationmethod based on recursive least square algorithm［J］.Mini-Micro Systems，2004，25（12）：2282－2285.

［4］孔祥玉，韓崇昭，馬紅光，等.基于Volterra級數的全解耦RLS自適應辨識算法［J］.系統仿真學報，2004，16（4）：807－809.

KONG Xiang-yu，HAN Chong-zhao，MA Hong-guang，et al.Fully decoupled RLS adaptive identification algorithm based on volterra series［J］.Journal of System Simulation，2004，16 （4）：807－809.

［5］孔祥玉，韓崇昭，馬紅光，等.一種總體最小二乘算法及在Volterra濾波器中的應用［J］.西安交通大學學報，2004，38（4）：339－342.

KONG Xiang-yu，HAN Chong-zhao，MA Hong-guang，et al.Total least square algorithm and its application to volterra filter［J］.Journal of Xi'an Jiao Tong University，2004，38 （4）：339－342.

［6］唐浩，屈梁生，溫廣瑞.基于Volterra級數的轉子故障診斷研究［J］.中國機械工程，2009，20（4）：447－454.

TANG Hao，QU Liang-sheng，WEN Guang-rui.Fault diagnosis for rotor system based on volterra series［J］.China Mechanical Engineering，2009，20（4）：447－454.

［7］Abbas H M，Bayoumi M M.Volterra system identification using adaptive genetic algorithms［J］.Applied Soft Computing，5（2004）：75－86.

［8］李志農，唐高松，肖堯先，等.基于自適應蟻群優化的Volterra核辨識算法研究［J］.振動與沖擊，2011，30 （10）：35－38.

LIZhi-nong，TANGGao-song，XIAOYao-xian，etal.Volterra series identification method based on adaptive ant colony optimization［J］.Journal of Vibration and Hock，2011，30 （10）：35－38.

［9］李志農，蔣靜，陳金剛，等.基于量子粒子群優化的Volterra核辨識算法研究［J］.振動與沖擊，2013，32（3）：60－63.

LI Zhi-nong，JIANG Jing，CHEN Jin-gang，et al.Volterra series identification method based on quantum particle swarm optimization［J］.Journal of Vibration and Hock，2013，32 （3）：60－63.

［10］李志農，蔣靜，馮輔周，等.基于量子粒子群優化Volterra時域核辨識的隱Markov模型識別方法［J］.儀器儀表學報，2011，32（12）：2693－2698.

LI Zhi-nong，JIANG Jing，Feng Fu-zhou，et al.Hidden markov model recognition method based on Volterra kernel identified with particle swarm optimization［J］.Chinese Journal of Scientific Instrument，2011，32（12）：2693－2698.

［11］Kennedy J，Eberhart R C.Particle swarm optimization［C］／／Proceedings of ICNN'95-IEEE International Conference on Neural Networks.IEEE，Piscataway，NJ，USA，1995：1942－1948.

［12］Eberhart R，Kennedy J.A new optimizer using particle swarm theory［C］／／Proc of 6th International Symposium on Micro Machine and Human Science，Nagoya，Japan.Piscataway NJ：IEEE Service Center，1995：39－43.

［13］毛鵬軒，肖揚.粒子群算法在穩定時滯系統設計中的應用［J］.計算機應用研究，2012，29（1）：214－216.

MAO Peng-xuan，XIAO Yang.Application of PSO algorithm for stable time-delay system design［J］.Application Research of Computers，2012，29（1）：214－216.

［14］崔志華，曾建潮.微粒群優化算法［M］.北京：科學出版社，2011.

［15］張浩，張鐵男，沈繼紅，等.Tent混沌粒子群算法及其在結構優化決策中的應用［J］.控制與決策，2008，23（8）：857－862.

ZHANG Hao，ZHANG Tie-nan，SHEN Ji-hong，et al. Research on decision-makings of structure optimization based on improved Tent PSO［J］.Control and Decision，2008，23 （8）：857－862.

［16］魏玉琴，戴永壽，張亞南，等.基于Tent映射的自適應混沌嵌入式粒子群算法［J］.計算機工程與應用，2013，49 （10）：45－49.

WEIYu-qin，DAIYong-shou，ZHAN Ya-nan，et al.Adaptive chaotic embedded particle swarm optimization algorithm based on Tent mapping［J］.Computer Engineering and Applications，2013，49（10）：45－49.

［17］Cui Z H，Cai X J，Zeng J C，et al.Particle swarm optimization with FUSS and RWS for high dimensional functions［J］.Applied Mathematics and Computation，2008，205（1）：98－108.

［18］Arumugam M S，Rao M V C.On the improved performances of the particle swarm optimization algorithms with adaptive parameters，cross-over operators and rootmean square（RMS）variants for computing optimal control of a class ov hybrid system［J］.Applied Soft Computing，2008，8（1）：324－336.

［19］Bajpai P，Singh S N.Fuzzy adaptive particle swarm optimization for bidding strategy in uniform price spotmarket ［J］.IEEE Transactions on Power System，2007，22（4）：2152－2160.

Parametric identification of nonlinear volterra model based on improved PSO algorithm

WEIXiao-juan，DINGWang-cai，LINing-zhou，ZHOU Xue-zhou

（School of Mechatronic Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China）

By combining the particle swarm optimization（PSO）with the chaotic optimization strategy and the control idea of population diversity，an improved particle swarm optimization（IPSO）algorithm was proposed for parametric identification of nonlinear Volterra seriesmodel.The basic idea of themethod was that the problem of nonlinear system identification was converted into an optimization problem in a high-dimensional parameter space.The chaotic optimization strategy was employed to increase the diversity of the initial population.By building dynamic subgroups，the optimization was realized through the collaboration of sub groups.The different adaptive adjustment strategies for control parameters of IPSO were used in subgroups.The convergencemeasure of IPSO was defined to perform the chaoticmutation operation reasonably.So the premature convergence was avoided，the speed and accuracy of IPSO were improved.In simulation tests，the proposed method was compared with Volterra model identification methods based on standard PSO algorithm，the genetic algorithm and the quantum-behaved PSO，respectively.Its effectiveness and robustness were verified.

improved particle swarm optimization algorithm（IPSO）；nonlinear system；Volterra series；system identification

TP18

A

10.13465／j.cnki.jvs.2015.21.019

國家自然科學基金項目（11162007，11462011）；甘肅省自然科學基金項目（1308RJZA149）

2014－05－23 修改稿收到日期：2014－08－22

衛曉娟女，博士生，副教授，1973年生

丁旺才男，教授，博士生導師，1964年生