懸臂疊層板狀結構穩定性研究

葉獻輝，范晨光，蔡逢春，張毅雄

（1.中國核動力研究設計院核反應堆設計技術重點實驗室，成都 610041；2.西南交通大學力學與工程學院，成都 610031）

懸臂疊層板狀結構穩定性研究

葉獻輝1，范晨光2，蔡逢春1，張毅雄1

（1.中國核動力研究設計院核反應堆設計技術重點實驗室，成都 610041；2.西南交通大學力學與工程學院，成都 610031）

將管道理論引入疊層板狀結構的流致振動研究，在勢流理論下，基于輸流管道的哈密頓原理，建立懸臂支承疊層板狀結構的流致振動模型，用微分求積法對模型的運動方程進行離散，運用特征值分析與響應分析結合的方法，確定系統失穩的臨界流速與形式，并研究不同參數對穩定性的影響。結果表明，懸臂疊層板發生顫振失穩，間隙，管／液質量比，間隙和流速非對稱參數對顫振流速有一定的影響，但在該研究參數范圍內對系統失穩形式沒有影響。

穩定性；微分求積法；疊層板；不可壓縮流；臨界流速

疊層板狀結構在反應堆結構工程中有重要的應用。當平行疊層板結構被安裝在剛性矩形管內時，冷卻流由于受到管道約束而呈現出管流特征。為研究方便起見，可以將這種結構近似視為管道結構。與管道不同的是，薄板所處的流體環境導致了單塊板上、下兩面存在著壓強差和流速差。在這種情況下，流體對單個板乃至整個疊層結構的振動都具有很強的耦合效應［1］。因此，對這種結構進行穩定性分析具有一定難度。

對該問題前人已有不少工作。早先人們發現冷卻劑流經管道時，由于兩側通道的壓強差和流速差，會使板產生屈曲破壞。國外較早的研究者大都采用單塊板模型，對流體的處理也較為初步。近年來，國內的研究取得了很大進展。郭長青等［2－3］采用板狀梁的力學模型，對疊層板結構的干模態的固有頻率和振型進行了研究；采用勢流理論導出的流體力研究了疊層板在流場中的固有頻率特性，并計算了其臨界流速。楊翊仁等［4－6］研究一個置于水槽中的多跨寬梁，考慮流體的黏性和耦合效應，求出了該模型中水的附加質量和阻尼，并將其推廣到疊層板狀梁結構中，獲得了靜水中的固有頻率和振型，與實驗做了比較；同時還利用假設模態法研究了Poiseuille流中剛性矩形管內的板狀梁的動力特性和穩定性［7］。陳貴清等［8］首先研究了有不可壓縮無黏流體的彈性矩形管內的簡支板狀梁的穩定性，而后研究了線性和非線性支承對發散臨界流速的影響［9－10］。由于疊層板狀結構類似于矩形輸流管道，本文針對這一特點，借鑒輸流管道對流體的處理方法，研究疊層板狀結構流固耦合系統的動力特性和臨界流速問題。

1 動力學方程

考慮如圖1所示的疊層板狀結構的管道模型。與梁式模型相同的是，將每個燃料板視為只有橫向振動的梁，不同的是，梁與梁之間與側壁共同構成了類似于管道的流體環境。為方便推導，進行下列假設：

（1）流體是無旋、無黏性，并且不可壓縮；

（2）模型X向兩側由薄板密封，但不約束疊層板Y向位移，不計上下流道流體交換；

（3）上、中、下三層板做梁式橫向彎曲變形，在長度方向不可伸長；

（4）結構做微幅振動；

（5）忽略重力和材料阻尼的影響。

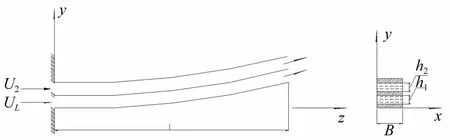
圖1 疊層板狀結構的管道模型Fig.1 Plate-type pipemodel

一端固支，另一端自由的三塊長度為L的彈性板相互平行，間隙中充滿水。下、中、上三塊板厚度分別為t1、t2、t3，單位長度質量為m1、m2、m3；下、上流道水的流速分別為U1和U2，單位長度質量為mf1、mf2；其它參數見圖1。

下、中、上三塊板的Y向位移分別用u1（z，t）、u2（z，t）和u3（z，t）表示，下、上間隙中面水的Y向位移用uf1（z，t）和uf2（z，t）表示。根據1、2假設，有uf1＝（u1+u2）／2，uf2＝（u2+u3）／2，mf1＝ρ1B（h1+u2－u1），mf1＝ρ1B（h2+u3－u2），其中ρ1為流體的密度。設ez和ey分別為Z向和Y向的單位向量，則流動速度Uf1和Uf2為

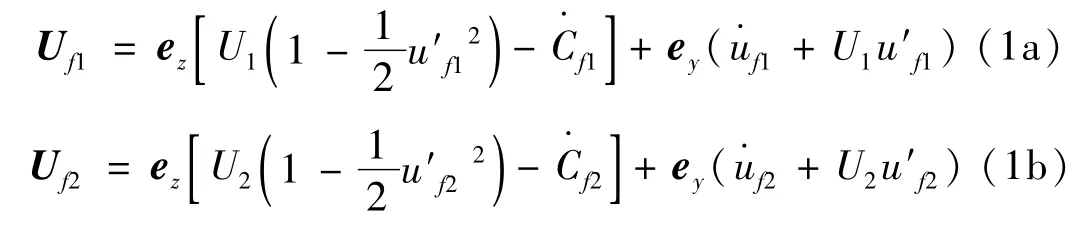
式中“′”和“·”分別表示對z和時間的微分，Cf1，Cf2為板彎曲引起流體在z負向上的位移，其大小為

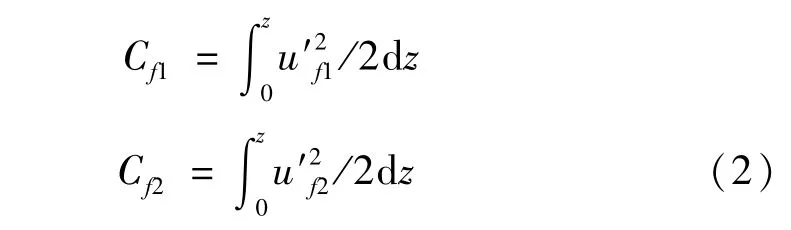
系統的拉格朗日函數是：

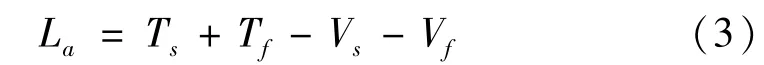
式中，Ts，Vs為板的動能和勢能；Tf，Vf為流體的動能和勢能，它們為

由于流體不可壓縮

自由端的位置向量R和與出口過流斷面垂直的單位向量τ分別為

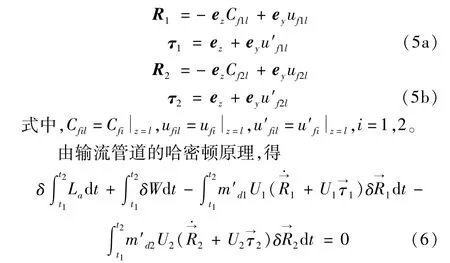
將式（1）～（5）代入式（6），外力虛功W為零，經過變分整理可得系統的運動微分方程

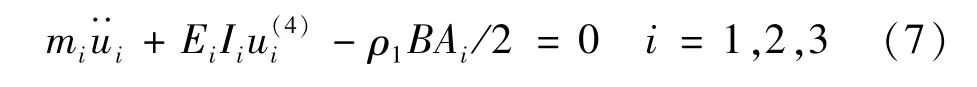
式中：

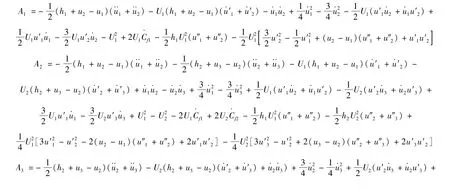
雖然在運動方程的推導中已經做了取舍，但式（7）仍非常復雜，為簡化問題，取

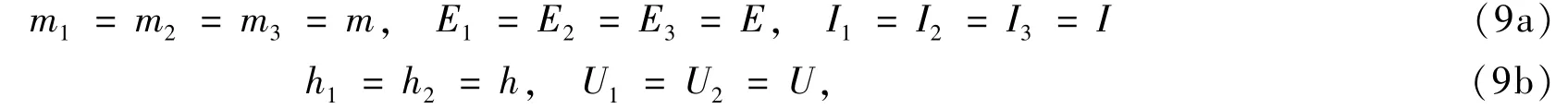
同時舍去高階項，然后將方程無量化并按文獻［1］對方程采用微分求積法離散，可得：

將式（10）與式（11）合并，得到一般形式

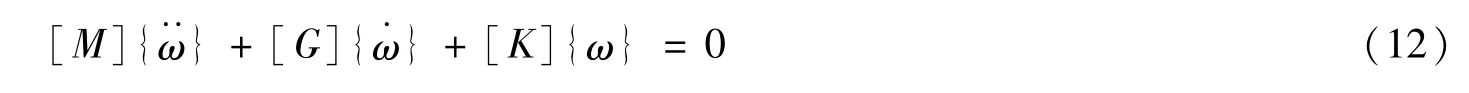
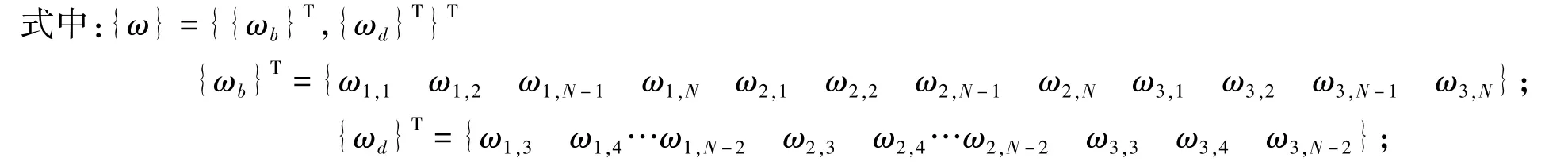
對式（14）求解，得到復數形式的Ω，其中Im（Ω）為系統的無量綱自振頻率。隨著流速的增大，可以得到對應于流速的一系列Ω值，當Re＞0，且Im（Ω）≠0時，系統發生顫振失穩；當Re（Ω）＞0且Im（Ω）＝0時，系統發生屈曲失穩。

2 疊層板狀結構的臨界流速和失穩特性

取結構幾何參數L＝0.4 m、B＝0.05 m、t＝0.002 m；材料密度ρ2＝8 400 kg／m3；彈性模量E＝98 GPa；間隙h1＝h2＝h＝0.01 m；流體密度ρ1＝1 000 kg／m3，代入式（14），采用Matlab計算系統Ω。

圖2給出了懸臂支承疊層板狀結構前7階模態的復頻率特性。當u很小時，頻率方程的根都是在復平面的下半部分或在虛數軸上。隨著流速的增加，1階特征值的實部最先是呈負向增長的趨勢，虛部則呈現出減小趨勢，當流速增大至某一值時，在圖2中為u＝6.8，系統1階特征值的虛部為0，而實部則出現了兩個分支。在實部軸上的，軌跡曾一度接近原點，但隨后又離開原點，沒有穿過虛軸進入不穩定區。通過對該流速段系統在流體激勵下的響應分析得知，系統經歷有阻尼的振動并未出現發散現象。圖3（a）給出了u＝7.0時上板中點響應的相圖。在這種情況下，1階模態沒有產生屈曲型不穩定。對于第4階頻率，隨著流速的增大，先是經歷了有阻尼的振動過程。當無量綱流速等于9.6時，第4階模態穿過虛軸進入復平面的上半部分，系統發生了顫振，此時有比較規則的振型，系統存在周期解，如圖3（b）為此時上板中點響應的相圖。當無量綱流速大于9.6時，系統產生了顫振型不穩定，圖3（c）給出了u＝10.2時上板中點響應的相圖。因此，u ＝9.6就是系統產生顫振失穩的臨界流速。

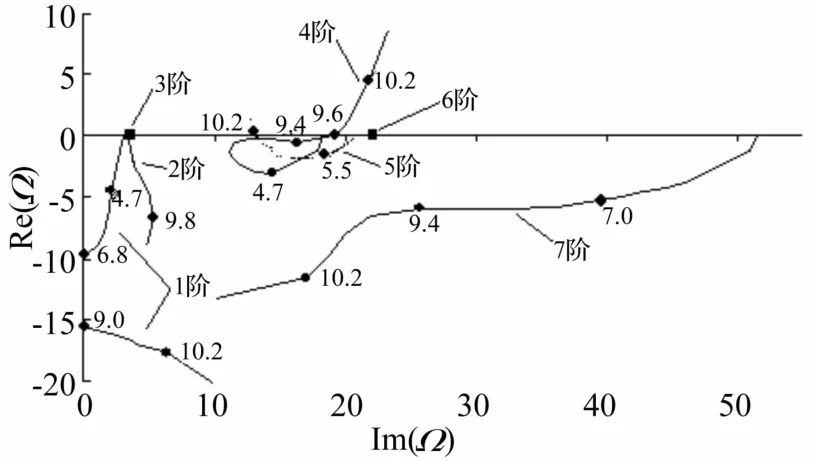
圖2 懸臂支承模型前7階的Argand圖Fig.2 The first7 frequencies Argand graph of the cantilevered model

圖3 模型響應的相圖Fig.3 The phase graph of the cantilevered model

3 不同參數對結構穩定性的影響

3.1 幾何參數的影響

板的間隙對結構的臨界流速有著重要的影響。圖4給出了間隙h在0.002～0.02 m之間變化時實際臨界流速的變化趨勢。從圖可以看出，在有量綱的情況下，隨著間隙的增大，最低臨界流速大體都呈下降趨勢。在h＝0.005m之前及h＝0.01m之后的趨勢較為明顯，在時，最低臨界流速呈現出先減小又增大的趨勢。在研究中發現，間隙的非對稱顯著影響著結構的固有頻率和響應。式（9b）取間隙非對稱參數γ＝h2／h1可推導式（10）類似方程，保持h1＝0.01 m，在0.5～2之間變化γ，其它參數不變，圖5給出了γ與臨界流速Ucr的關系圖。由圖5可知，間隙非對稱參數γ對臨界流速的影響基本上與板的間隙對臨界流速的影響趨勢大致相同。在本文研究的參數變化范圍內，γ在0.9附近時，有最大的臨界流速，但沒有發現間隙非對稱參數對結構的失穩類型有影響。

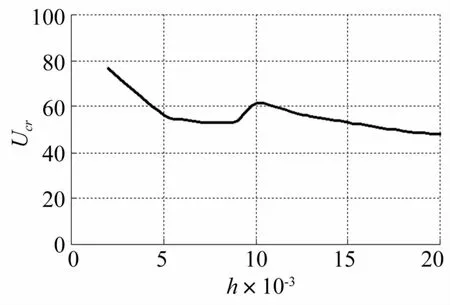
圖4 h與臨界流速Ucr關系圖Fig.4 h vs Ucr

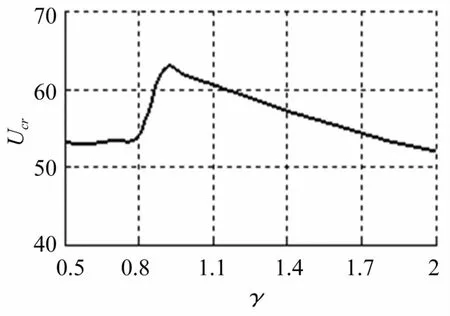
圖5 γ與臨界流速Ucr關系Fig.5γvs Ucr

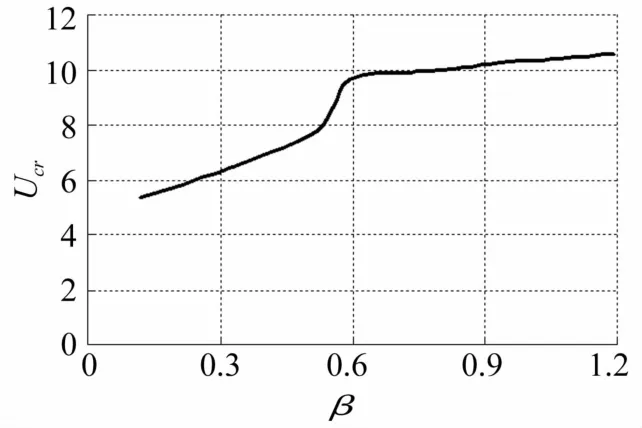
圖6 β與臨界流速Ucr關系Fig.6βvs Ucr

3.2 質量參數的影響

圖6給出了質量無量綱量參數β與無量綱臨界流速Ucr的關系曲線。從圖6得知，最低無量綱臨界流速隨無量綱量β的增大呈上升趨勢。這是因為，在回轉守恒系統中，結構由于發散而失去穩定，即在臨界流速下，無量綱頻率為零。發散是一種靜力現象，因此時間相關項不影響臨界流速。文獻［11］中研究了在不同的β值時，一根兩端簡支管道的頻率比與無量綱流速的關系，表明：“對應于不同β值的頻率，在同樣的無量綱流速下變為零”，“只要系統是回轉守恒系統，則確定發散的臨界流速的方法與確定一個梁承受軸向壓縮力而失穩的方法一樣”。

3.3 上下流道流速不等的影響

當結構上下兩個流道存在流速差時，由于同時存在兩個流速，此時臨界流速的概念需要做如下補充。定義λ＝U2／U1，當參數取定后，結構發生失穩所對應的兩個流速中較小者稱作對應于λ的臨界流速。式（9b）取流速非對稱參數λ可推導式（10）類似方程，在0.5～2之間變化無量綱參數λ，其他參數不變，圖7給出了lnλ與對應于λ的無量綱臨界流速Ucr的關系圖。由圖7可知，對應于λ的無量綱臨界流速都在lnλ＝0（即λ＝1）時達到最大，流速差越大，對應于λ的無量綱臨界流速越小。在本文研究的參數變化范圍內，沒有發現無量綱流速非對稱參數對結構的失穩類型有影響。

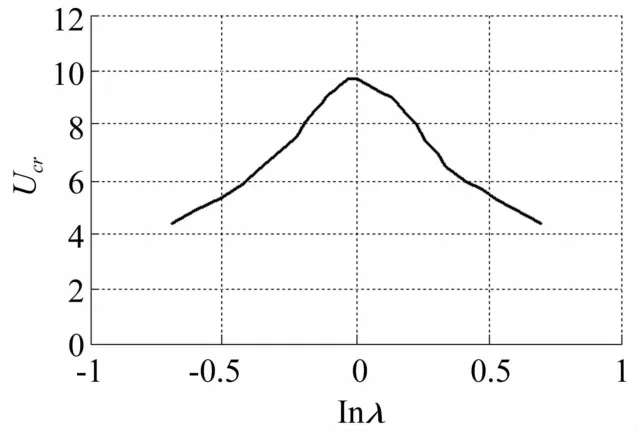
圖7 Inλ與臨界流速Ucr關系Fig.7 Inλvs Ucr

4 結 論

本文運用管道理論對懸臂疊層板狀結構力學模型進行了較為系統的動力學研究。將微分求積法引入疊層板狀結構運動方程的數值求解。運用特征值分析與響應分析結合的方法，研究了系統失穩的臨界流速與失穩形式，并探討了不同參數對系統失穩值的影響。算例分析研究表明：懸臂疊層板以顫振的形式發生失穩。顫振臨界隨著管／液質量比的增加而增加；隨著上下流道流速差的增加而減小；隨間隙的增加，臨界流速先減小后增大，大于0.01后顫振速度減小；隨間隙非對稱參數不是單調變化，在0.9附近時有最大的臨界流速。間隙，管／液質量比，間隙和流速非對稱參數對顫振流速有一定的影響，在本文研究參數范圍內對系統失穩形式沒有影響。

［1］范晨光，楊翊仁.疊層板狀結構流致振動特性研究［J］.工程力學，2007，24（1）：31－36.

FAN Chen-guang，YANG Yi-ren.Study on flow-induced vibration of a laminated-plate-type structure［J］.Engineering Mechanics，2007，24（1）：31－36.

［2］郭長青，張兆湘，鄒長川.疊層板型元件模型干模態固有頻率與振型分析［J］.中南工學院學報，1995，9（1）：18－23.

GUO Chang-qing，ZHANG Zhao-xiang，ZOU Chang-chuan.Analysis on dry-modal natural frequencies and modes of an experimentalmodel for parallel-plate assembly［J］.Journal of Central-South Institute of Technology，1995，9（1）：18－23.

［3］Guo C Q，Peng R H，Sun D L.A Dynamic model for flowinduced vibration of parallel plate fuel assemblies［C］／／Transaction of the 12th International Conference on Structural Mechanics in Reactor Technology，Stuttgart，1993.

［4］Yang Y R，Zhang JY.Frequency analysis of a parallel flat plate-type structure in still water，Part I：amulti-span beam ［J］.Journal of Sound and Vibration，1997，203（5）：795－804.

［5］Yang Y R，Zhang JY.Frequency analysis of a parallel flat plate-type structure in stillwater，Part II：a complex structure ［J］.Journal of Sound and Vibration，1997，203（5）：805－814.

［6］楊翊仁，張繼業，馬建中.不可壓縮粘性流中板狀梁的附加質量及阻尼［J］.核動力工程，1998，19（5）：443－449.

YANG Yi-ren，ZHANG Ji-ye，MA Jian-zhong.Added mass and damping of plate-type beam vibrating in incompressible viscous fluid［J］.Nuclear Power Engineering，1998，19（5）：443－449.

［7］魯麗，楊翊仁.矩形管內不可壓縮粘性流中簡支梁的穩定性［J］.西南交通大學學報，2001，36（6）：561－564.

LU li，YANG Yi-ren.Stability of pinned-pined beam in a rectangular tube filled with incompressible viscous fluids［J］.Journal of Southwest Jiaotong University，2001，36（6）：561 －564.

［8］陳貴清，楊翊仁.板狀梁結構流致振動及其穩定性分析［J］.河北理工學院學報，2002，4：105－113.

CHEN Gui-qing，YANG Yi-ren.Study on flow-induced vibration and stability for a plate-type beam structure［J］.Journal of Hebei Technology college，2002，4：105－113.

［9］陳貴清，楊翊仁.受非線性支承的板狀梁結構流致振動研究［J］.固體力學學報，2003，24（3）：277－283.

CHEN Gui-qing，YANG Yi-ren.Study on flow-induced vibration for a plate-type beam structure with nonlinear support［J］.Acta Mechanica Solida Sinica，2003，24（3）：277－283.

［10］Chen GQ，Yang Y R.Flow-induced vibration of a plate-type beam with elastic support［C］／／ICVE'2002，Nanjing，China，2002：108－111.

［11］Chen SS.圓柱型結構的流體誘發振動［M］.北京：石油工業出版社，1993.

Stability of a cantilever lam inated-p late structure

YE Xian-hui1，FAN Chen-guang2，CAIFeng-chun1，ZHANGYi-xiong1

（1.Key Laboratory of Reactor System Design Technology，China Nuclear Power Research and Design Institute，Chengdu 610041，China；
2.School of Mechanics and Engineering，Southwest Jiaotong University，Chengdu 610031，China）

The pipe theory was introduced into the flow-induced vibration study of a laminated plate-type structure.Themechanicalmodelwas set to describe the plate-type structure in potential flow.The dynamic equation was deduced based on Hamilton principle.The differential quadrature method was used to solve the differential equations.And the effects of various parameters on the instability of the system were investigated.The results showed that the cantilevered model has the flutter over the critical flow velocity；parameters of gap，mass ratio，gap asymmetrical parameter and velocity asymmetrical parameter have influences on the flutter velocity，but they have no effect on the system's instability forms in the ranges of parameters considered here.

stability；differential quadraturemethod；plate-type structure；uncompressible flow；critical flow velocity

O323

A

10.13465／j.cnki.jvs.2015.21.031

國家自然科學基金青年基金（11102170）資助項目

2014－03－31 修改稿收到日期：2015－03－25

葉獻輝男，博士，高級工程師，1980年生