單磁鐵懸浮系統自激振動的穩定性分析及抑制

黎松奇， 張昆侖

(西南交通大學磁浮技術與磁浮列車教育部重點實驗室，四川成都 610031)

EMS型磁懸浮列車作為一種新型的交通工具，在其理論研究和工程實踐中，出現了一些特有的現象.在德國和日本的列車運行實驗中均出現了車輛結構性振動的情況，即使車體靜態懸浮，也可能與軌道以及橋梁產生自激振動[1].多年以來，各國專家一直在研究和探討該問題[2].

文獻[3]對磁浮車調試過程中出現的鋼軌道框架和車輛共振現象進行了理論研究，指出磁浮車二次懸掛和鋼框架的垂向頻率相同會引起系統共振.文獻[4]用Nyquist準則分析了簡化車-軌系統的穩定性，提出了使用虛擬調諧質量阻尼器控制振動的方法.文獻[5]采用諧波平衡法分析了磁懸浮系統非線性振動現象，證明了只要軌道存在彈性，車-軌耦合振動不可避免.文獻[6]通過系統的開環傳遞函數和相頻曲線分析了系統穩定的充分條件，為系統設計提出了基本的穩定性要求.文獻[7]利用中心流形對各種耦合振動的情況進行了分岔方程的推導以及仿真分析.文獻[8-9]通過數值仿真的方法對車體以及彈性橋梁在耦合振動過程中的動力學行為進行了分析.文獻[10-11]研究了控制系統時滯對于磁浮車-軌非線性耦合振動的影響.文獻[12]建立了通過全狀態反饋控制的單磁鐵懸浮系統，討論了通過粒子群算法對控制器參數優化的具體方法.

在上述文獻中沒有在理論上對懸浮控制器參數以及車-軌系統參數在靜態懸浮過程中對于穩定性的影響給出較好的解釋.本文通過建立簡化的單磁鐵懸浮系統車體-懸浮架-軌道系統動力學模型，對磁浮列車靜態懸浮自激振動穩定性問題進行了分析，討論了系統參數對于穩定性的影響，給出了系統主要參數和穩定性之間關系的表達式，并討論了運用瞬時最優控制抑制車-軌自激振動的具體方法.

1 車輛-軌道系統的數學模型

1.1 車輛動力學方程

本文主要分析起浮后車輛靜態懸浮時發生的自激振動，所以只考慮車輛-懸浮架-軌道的垂向自由度，忽略二系懸掛和軌道形變以外的其他干擾.簡化的單磁鐵懸浮系統力學模型如圖1所示.

圖1中:

fe為電磁吸力;

m2、m3分別為懸浮架和車體的質量;

z1、z2分別為懸浮架和車體的實際位移;

h為軌道的位移;

c為懸浮架與軌道之間的距離;

x為車體橫向位移;

k3為二系懸掛剛度;

c3為二系懸掛阻尼.

系統中參考方向取向下為正.

圖1 單磁鐵懸浮系統力學模型Fig.1 Mechanical model of single magnet suspension system

由圖1所示模型可知 c=z1－h，同時，懸浮架和車體的動力學方程為

式中:

Fs為二系懸掛產生的力，

其中，F0為二系懸掛在平衡點的力.

電磁鐵產生的吸力可表示為

式中:N為線圈匝數;

A為有效面積;

μ0為真空磁導率;

i為線圈電流.

在平衡點(i0，c0)處求偏導可得

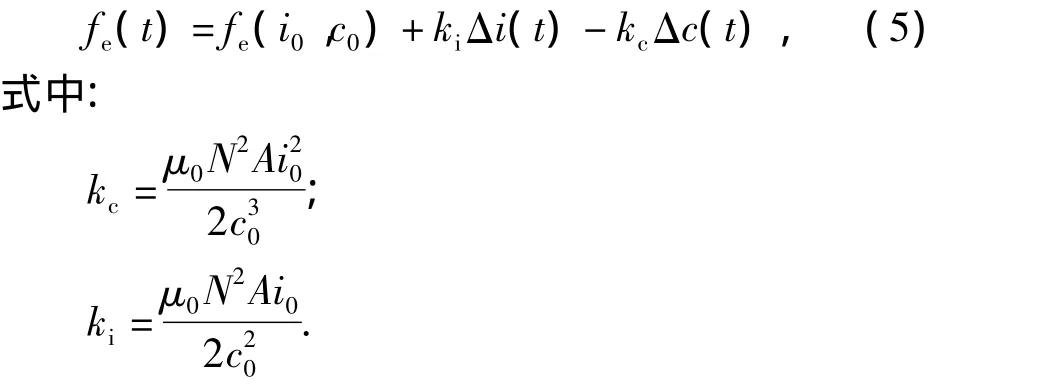
目前有多種方法控制電流對于電壓的滯后[13]，本文直接使用電流作為控制輸入.采用工程中常用的PID算法，令:c為間隙，c'為間隙變化速度，z″1為懸浮架加速度為反饋變量，kp、kv、ka為控制器參數，c0為額定的懸浮氣隙，控制電流表示為

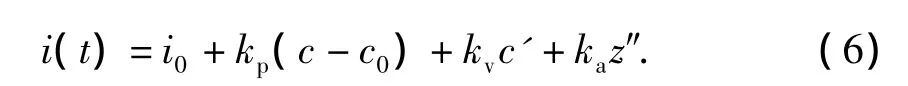
聯立式(1)、(5)、(6)，可求得平衡點處fe-c的關系.

令:k2為平衡點處的等效磁隙剛度;c2為平衡點處的等效磁隙阻尼.則fe(t)又可以表示為

1.2 軌道動力學方程

軌道模型采用在磁浮系統研究中廣泛使用的Bernoulli-Euler(BE)梁方程

式中:

EI為抗彎剛度;

c為軌道阻尼;

ρA為軌道線密度;

F(x，t)為負載.

采用模態分解法處理后得軌道位移的微分方程為

式中:Mn為廣義質量;

Φn(x)為軌道第n階模態;

Qn(t)為第n階的廣義力;

εn為軌道的n階阻尼比;

ωn0為軌道n階固有頻率;

L為軌道長度.

由式(11)可得

當單獨考慮第n階模態作用時，令:

則軌道位移方程可表示為

綜上所述，當單獨考慮第n階模態作用時，系統的動力學方程可以表示為

2 振動穩定性分析

先考慮軌道一階模態單獨作用的情況，將式(13)移動到平衡點，令:

為狀態變量，得到系統狀態矩陣為

系統的特征方程為

式中:I為單位矩陣.

系統穩定的基本條件為 ai＞0(i=0，1，2，…，6)，則系統穩定必須能滿足 b3＞0，b4＞0，b5＞0，b6＞0.代入b1～b6值，整理得到軌道一階模態單獨作用下系統穩定的條件為

同理，當軌道第n階模態單獨作用時，穩定條件為

當系統控制參數不變時，二系懸掛參數和軌道參數的基本關系為

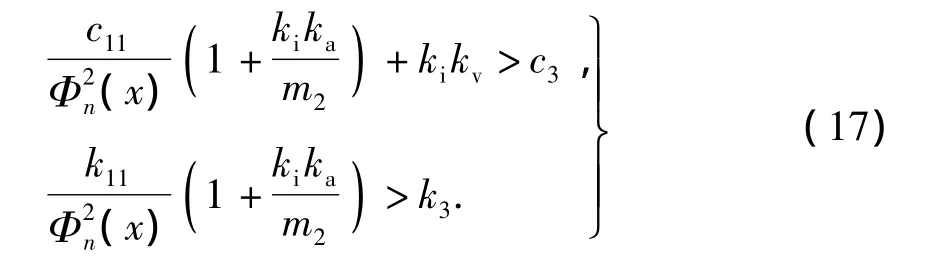
故軌道模態階數越大，k1n和c1n值也越大，所以，當軌道一階模態單獨作用時能滿足式(15)，其他模態單獨作用時也能滿足式(16).

綜上所述，在選用c、c'和z″1為控制器反饋變量時，系統穩定性條件如式(15)所描述.代人k1n和c1n解析式，分析可知:

(2)軌道的抗彎剛度EI越大，系統越穩定;軌道結構阻尼越大，系統越穩定;軌道長度L越小，系統越穩定，但為了提高穩定性而修改以上3個參數，都會顯著增加線路的成本;

(3)車體質量m2越小，系統越穩定，該條件對車體的輕量化設計提出了要求;

(4)系統的控制器參數影響穩定性，被控制器參數決定的k2和c2過大或者過小都不利于系統穩定，同時考慮到系統需要產生能保持在平衡點的力，k2滿足

(5)由式(15)、(16)可知，由于系統穩定性和系統成本相互矛盾，所以在一定的軌道和車輛參數條件下，系統可能產生劇烈的自激振動;在系統參數滿足式(17)的情況下，通過調節控制參數可以使系統穩定性增加，使自激振動變小;如果系統控制參數無論如何調節，都無法滿足式(17)時，只能通過修改系統物理參數的方法減小振動，如k1n非常小(當EI非常小，或者L非常大).

3 抑制振動的瞬時最優算法

從前面的分析可知，當系統滿足式(17)時，穩定性可以通過控制器參數調節，此時系統可以通過調節k2或c2取值增加系統穩定性.從式(7)中參數可以看出，當系統固定時由于ki和kc是常量，所以k2取值需由控制參數kp和ka調節，c2取值可以通過kv和ka調節.且由于調節ka會改變系統慣性，其作用相當于改變了系統的質量，通常采用調節kp和kv的方法.

本文采用瞬時最優控制算法來確定控制器參數的具體取值.該方法與傳統的最優控制算法相比，并不是求取整個過程中的全局最優指標，而是針對任意時刻取局部最優指標，能夠避免求解在傳統的最優控制中使用Riccati方程，在工程應用中能夠實現快速的計算.

瞬時最優算法的描述如下.

系統運動方程描述為

式中:y(t)為位移向量;

M、C、K分別是系統質量矩陣、阻尼矩陣和剛度矩陣;

f(t)為外激勵向量;

D為外激勵向量的位置矩陣;

u(t)為主動控制力向量;

E為控制力位置矩陣.

可將式(18)改寫為狀態空間形式

x'(t)=A2x(t)+Bu(t)+Hf(t)，

式中:

取性能指標[14]

式中:Q和R為權矩陣，分別代表結構和控制力的強調程度.

求解式(19)是約束條件下系統最優控制問題，可得瞬時最優控制力為

式中:

Δt為控制算法的時間間隔.

當單磁鐵懸浮模塊發生振動時，取z1、z'1、c 和c'為補償反饋，可由式(20)直接求出抑制振動的瞬時最優補償力u(t)，代人式(7)，根據一定的權重分解出需要的k2和c2，再通過k2、c2與控制器參數關系求解kp和kv的取值，最后根據補償值修正控制器參數.懸浮控制系統工作的原理如圖2所示.

圖2 懸浮控制系統工作原理Fig.2 Working principle of the suspension control system

4 系統仿真

本文采用Matlab中的Simulink工具箱建模，進行車-軌振動數值仿真.采用某磁浮車-軌系統的主要參數如下:車體質量為2 000 kg，懸浮模塊質量為750 kg，磁鐵面積為0.024 m2，軌道線密度為6 900 kg/m，軌道阻尼比為 0.005，軌道長度為24.8 m，軌道抗彎剛度為 2.43 ×104MN·m2，額定懸浮間隙為0.008 m，二系懸掛剛度為50 kN/m，二系懸掛阻尼為10 kN/(m/s)，懸浮架橫向位置L/2.

為簡化表達，令:

車體在t=0時刻開始起浮，記錄系統20 s內的振動情況，ωc為控制器特征頻率，ωs為二系懸掛固有頻率.

(1)參數正常情況

當仿真中系統參數都取正常情況(仿真1)，結果如圖3(a)所示，車體迅速到達平衡狀態，懸浮架與軌道振動隨著時間減小.放大圖形可以看出，車-架-軌振動的主要頻率來自于二系懸掛.

計算系統穩定條件(式(15)):

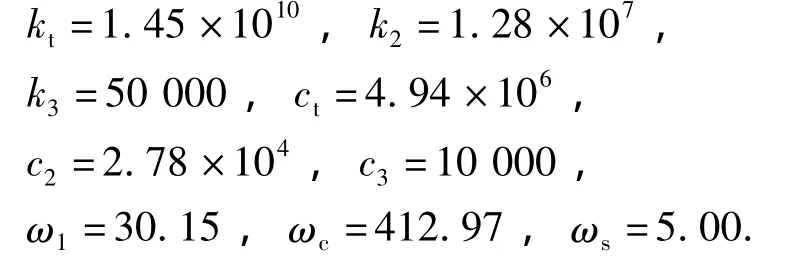
可見在系統參數正常的情況下，有

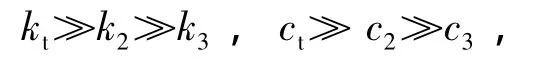
而且ω1、ω2和ω3之間隔得很遠，系統難以發生劇烈自激振動.當參數都在正常范圍內變化時，系統總能穩定.

從圖3中可見，由于軌道和二系懸掛具有彈性，系統總會產生振動[5]，而各參數會影響振動幅值的大小和衰減速度，所以對于系統物理參數已經固定的車-軌系統，主要研究的內容是如何通過調節控制器參數抑制振動，使振動的振幅減小，同時快速衰減.

瞬時最優控制從 t=0時刻開始工作(仿真2)，仿真結果如圖3(b)所示.可以看出振動被更好的抑制，系統起浮10 s時，懸浮氣隙振幅與軌道振幅分別減少了59%、48%.

(2)二系懸掛參數改變

當車體質量取0.25m1，二系懸掛剛度取2k3，車體起浮后情況如圖3(c)所示(仿真3).由于k3增加，系統穩定性減小，振動大于標準參數情況.瞬時最優控制從t=0時刻開始工作，仿真結果如圖3(d)所示(仿真4)，振動被有效抑制，10 s時，懸浮氣隙振幅與軌道振幅分別減少了62%、94%.

圖3 車-軌振動位移仿真結果Fig.3 Simulation results of vehicle-track vibration displacement

仿真中計算出的參數如下:

(3)軌道參數改變

當軌道長度取1.2L，軌道抗彎剛度取0.8EI，車體起浮后情況如圖3(e)所示(仿真5).仿真中發現系統自激振動對軌道參數改變很敏感，車體-軌道振幅大幅增加，振動衰減變慢.瞬時最優控制從t=0時刻開始工作，仿真結果如圖3(f)所示(仿真6)，系統振動快速衰減，10 s時，懸浮氣隙振幅與軌道振幅分別減少了5%、73%.

仿真中計算出的參數如下:

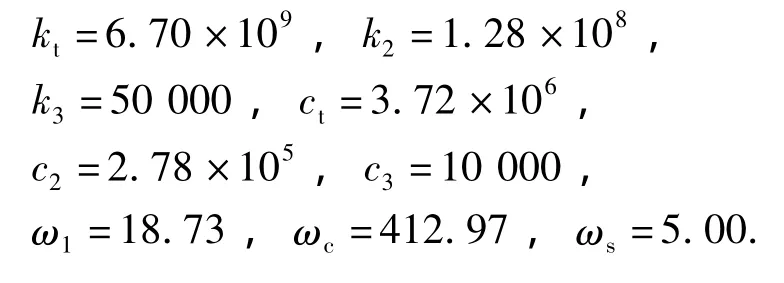
5 結束語

針對列車起浮后與軌道相互耦合發生自激振動的現象，本文通過建立模型分析了車輛-軌道系統的振動穩定性，給出了系統主要參數和穩定性的關系.研究發現，磁浮車體-懸浮架-軌道在正常參數范圍內總能滿足系統絕對穩定的基本條件，但系統各主要參數對于振動幅值大小、振動衰減速度有直接的影響.在系統物理參數不變的情況下，可以通過瞬時最優控制算法調節懸浮控制器參數抑制車-軌自激振動.通過數值仿真驗證了系統參數與穩定性的關系以及控制方法對振動抑制的有效性.結論可供磁浮車輛-軌道系統設計參考.

致謝:西南交通大學青年教師百人計劃項目資助(SWJTU2011BR052EM).

[1]趙春發.磁懸浮車輛系統動力學研究[D].成都:西南交通大學，2002.

[2]翟婉明，趙春發.磁浮車輛/軌道系統動力學(Ⅰ):磁/軌相互作用及穩定性[J].機械工程學報，2005，41(7):1-10.

ZHAI Wanming，ZHAO Chunfa.Dynamics of maglev vehicle/guideway sysystems(Ⅰ):magnet/rail interaction and system stability[J].Chinese Journal of Mechanical Engineering，2005，41(7):1-10.

[3]李莉，孟光.慢起慢落時磁浮車輛與鋼軌道框架耦合共振分析[J].振動與沖擊，2006，25(6):46-48.

LI Li，MENG Guang.Analysis on resonance vibration of maglev trains suspending or loading on steel track frame[J].Journal of Vibration and Shock，2006，25(6):46-48.

[4]ZHOU D F，HANSEN C H，LI J.Suppression of maglev vehicle-girderself-excited vibration usinga virtual tuned mass damper[J].Journal of Sound and Vibration，2011，330(5):883-901.

[5]施曉紅，龍志強.磁懸浮車軌耦合控制系統的非線性振動特性分析[J].鐵道學報，2009，31(4):38-42.

SHI Xiaohong，LONG Zhiqiang.Nonlinear vibration analysis of the maglev guideway-vehicle coupling control system[J].Journal of the China Rrailway Society，2009，31(4):38-42.

[6]洪華杰，李杰，張錳.磁浮車軌耦合系統穩定性分析[J].控制理論與應用，2006，23(3):421-428.HONG Huajie，LI Jie，ZHANG Meng.Stability analysis of magnetic levitation system with vehicle-guideway interaction[J]. Journal of Control Theory and Applications，2006，23(3):421-428.

[7]鄒東升，佘龍華，張志強，等.磁浮系統車軌耦合振動分析[J].電子學報，2010，38(9):2071-2075.

ZOU Dongsheng，SHE Longhua，ZHANG Zhiqiang，et al.Maglev vehicle and guideway coupling vibration analysis[J].Acta Electronica Sinica，2010，38(9):2071-2075.

[8]黎松奇，張昆侖.磁浮列車車軌耦合振動仿真研究[J].計算機仿真，2014，31(8):137-141.

LI Songqi，ZHANG Kunlun.On simulation of track coupling vibration formaglev train[J]. Computer Simulation，2014，31(8):137-141.

[9]梁鑫，羅世輝，馬衛華，等.磁浮列車單鐵懸浮車橋耦合振動分析[J].交通運輸工程學報，2012，12(2):32-37.

LIANG Xin，LUO Shihui，MA Weihua，et al.Coupling vibration analysis of single-magnet suspension vehiclebridge for maglev train[J]. Journal of Traffic and Transportation Engineering，2012，12(2):32-37.

[10]王洪坡，李杰.一類非自治位置時滯反饋控制系統的亞諧共振響應[J].物理學報，2007，56(5):2504-2516.

WANG Hongpo，LI Jie.Sub-harmonic resonances of the non-autonomoussystem with delayed position feedback control[J]. Acta Physica Sinica，2007，56(5):2504-2516.

[11]ZHANG Lingling，HUANG Lihong，ZHANG Zhizhou.Hopf bifurcation of the maglev time-delay feedback system via pseudo-oscillator analysis[J].Mathematical and Computer Modelling，2010，52(5/6):667-673.

[12]WANG Hui，SHEN Gang，ZHOU Jinsong.Control strategy of maglev vehicles based on particle swarm algorithm[J]. JournalofModern Transportation，2014，22(1):30-36.

[13]李云鋼，常文森.磁浮列車懸浮系統的串級控制[J].自動化學報，1999，25(2):247-251.

LI Yungang，CHANG Wensen.Cascade control of an ems maglev vehicle's levitation control system[J].Acta Automatica Sinica，1999，25(2):247-251.

[14]李宏男，李忠獻，祁皚，等.結構振動與控制[M].北京:中國建筑工業出版社，2005:356-359.