Brauer特征標的誘導與限制

王 堅，曾吉文

（1.龍巖學院數(shù)學與計算機科學學院，福建龍巖364012；2.廈門大學數(shù)學科學學院，福建廈門361005）

Brauer特征標的誘導與限制

王 堅1，曾吉文2*

（1.龍巖學院數(shù)學與計算機科學學院，福建龍巖364012；2.廈門大學數(shù)學科學學院，福建廈門361005）

設H?G且χ∈Irr（G），φ∈IBr（G），Cossey等給出了χ=βG對χH的每個不可約成分β都成立的一個充分條件；同時，給定β∈Irr（H），也得到了一個使β=χH對βG的每個不可約成分χ都成立的條件·我們通過討論φ的零化元，給出了（φH）G是φ的倍數(shù)的一個刻畫·對偶地，對于α∈IBr（H），也給出了（αG）H是α的倍數(shù)的一個刻畫·

Brauer特征標；p-正則元；零化元

若χ是G的一個常特征標，則V（χ）是由G中所有滿足χ（x）≠0的元素x生成的子群·這個非零化子群很顯然是G的唯一的最小的子群V使得χ在G￣V中零化·此外，因為χ是G的一個共軛類函數(shù)，所以V（χ）G·類似的，我們可以定義一個Brauer特征標的非零化子群·若φ是G的一個Brauer特征標，則V（φ）是由G中所有滿足φ（x）≠0的p-正則元x生成的子群·這是使得φ在G0￣V0中零化的唯一最小子群·類似的，V（φ）G·

1 預備知識

受文獻［1］的啟發(fā)，從誘導特征標的定義出發(fā)來討論Brauer特征標的誘導、限制與零化元之間的關系.下面引進一些記號，G指一個有限群，p是一個固定素數(shù)· G0是p-正則元的集合，即IBr（G）是G的不可約p-Brauer特征標的集合·設H?G，coreG（H）指包含于H的G的最大的正規(guī)子群·為方便起見，當素數(shù)p選定之后，將p-Brauer特征標簡寫為Brauer特征標·其他的記號，可參見文獻［2］·

2 主要結果

定理1 設H?G且φ∈IBr（G），令N= coreG（H）.則下列條件等價.

1）（φH）G是φ的倍數(shù)·

2）φ在G0￣N0中零化·

3）φ在G0￣H0中零化·

對任意的x∈G0，有

因為φ是G的G0上的共軛類函數(shù)，當y∈H0與x關于G共軛，可以得出·從而

其中m是g∈G中滿足gxg￣1∈H的g的數(shù)目·

首先設（φH）G是φ的倍數(shù)·通過計算次數(shù)可以得到（φH）G=｜G∶H｜φ，因此對于任意的x∈G0，有

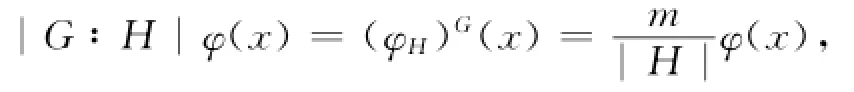
其中m如上所述·若φ（x）≠0，則m=｜G｜并且對任意的g∈G，gxg￣1∈H，從而有x∈N·因此得到了2）·

反過來，設φ在G0￣N0中零化·通過比較（φH）G與｜G∶H｜φ在G0上的取值來推出它們相等·若x?N0，則，其中m如上所示：此時｜G∶H｜φ（x）=0·若x∈N0，則（φH）G（x）=｜G∶H｜φ（x）·因此命題得證·

上述定理中的條件（φH）G是φ的倍數(shù)等價于（φN）G是φ的倍數(shù)·在這種情形下，φN的一個不可約成分θ關于G的誘導也是齊次的，從而根據(jù)Clifford定理θ關于IG（θ）的誘導也是齊次的，其中IG（θ）是θ在G中的穩(wěn)定化子，當p≠5時，由文獻［3］的主要結果可以得到IG（θ）/N可解·

證明 設φ是ρG的一個在G0￣N0中零化的不可約成分·根據(jù)定理1應用到H=N，則（φN）G是φ的倍數(shù)·根據(jù)文獻［2］的推論8.7，ρ是φN的不可約成分，因此ρG是φ的倍數(shù)，并且φ是ρG的唯一的不可約成分·

反過來，設φ是ρG的唯一的不可約成分·根據(jù)文獻［2］的推論8.7，φN的每個不可約成分ζ都與ρ關于G共軛，根據(jù)文獻［4］的第3章的引理1.8，ζG=ρG是φ的倍數(shù)，因此（φN）G是φ的倍數(shù)·所以，根據(jù)定理1，φ在G0￣N0中零化·

下面討論H的不可約Brauer特征標α誘導到G再限制到H后是α的倍數(shù)的情況.

定理2 設H?G且α∈IBr（H），令N= coreG（H），則下列條件等價：

1）（αG）H是α的倍數(shù)·

2）αN是G-不變的并且α在H0￣N0中零化·

證明 對任意的x∈G0，

首先，設（αG）H是α的倍數(shù)·當x，y∈H0關于G共軛時，易得α（x）=α（y）·特別地，αN是G-不變的·

設h∈H0，若ghg￣1∈H，則.α（ghg￣1）= α（ghg￣1）=α（h），從而αG（h）=（m/｜H｜）α（h），其中m如定理1證明所述·

因為（αG）H是α的倍數(shù)，比較次數(shù)可以知道（αG）H=｜G∶H｜α，從而，對于h∈H0，有

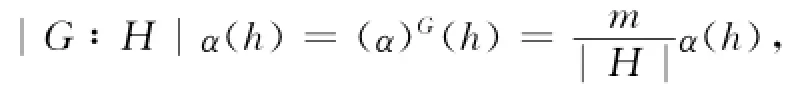
其中m如上所述·若α（h）≠0，則m=｜G｜并且對任意的g∈G，ghg￣1∈H，從而有h∈N·因此α在H0￣N0中零化·

反之，若αN是G-不變的并且α在H0￣N0中零化·為了推出（αG）H=｜G∶H｜α，我們證明（αG）與α對任意h∈H0取值都相等·首先，設h?N，則α（h）=0，從而｜G∶H｜α（h）=0·下面來證明αG（h）=0，對任意的g∈G，若ghg￣1?H，則.α（ghg￣1）=0；若ghg￣1∈H，則ghg￣1?N，從而.α（ghg￣1）=α（ghg￣1）=0·若h∈N，則.α（ghg￣1）=α（ghg￣1）=α（h）·因此，αG（h）=｜G∶H｜α（h）·

注 在定理2中，因為αN是G-不變的且α在H0￣N0中零化·從而V（α）=V（αN）G·當p ｜G｜，根據(jù)文獻［2］的定理2.12，IBr（G）=Irr（G）且G0=G，上面3個結論分別推廣了文獻［1］的定理2.1、推論2.2以及定理2.3·

［1］ Cossey J P，Isaacs I M，Lewis M L.Induction and restriction of characters and Hall subgroups［J］.J Algebra，2013，383：129-143.

［2］ Navarro G.Characters and blocks of finite croups［M］.Cambridge：Cambridge University Press，1998：24，158，273-276.

［3］ Navarro G，Sp?th B，Tiep P H.On fully ramified Brauer characters［J］.Adv Math，2014，257：248-265.

［4］ Nagao H，Tsushima Y.Representations of finite groups［M］.Boston：Academic Press，1989：172.

Induction and Restriction of Brauer Characters

WANG Jian1，ZENG Ji-wen2*
（1.Department of Mathematics and Computer Science，Longyan University，Longyan 364012，China；2.School of Mathematical Sciences，Xiamen University，Xiamen 361005，China）

Let H?G，χ∈Irr（G）andφ∈IBr（G）.Cossey obtain a sufficient condition forχ=βG，whereβ∈Irr（χH）.Simultaneously，given a characterβ∈Irr（H），they get a condition satisfyβ=χH for every irreducible constituentχofβG.In this paper we determine when it happens that（φH）Gis a multiple ofφby investigating the vanishing elements ofφ.Dually，we give a description to determine that（αG）His a multiple ofαforα∈IBr（H）.

Brauer character；p-regular element；vanishing element

O 152.6

A

0438-0479（2015）04-0502-02

10.6043/j.issn.0438-0479.2015.04.011

2014-09-08 錄用日期：2014-11-20

龍巖學院博士科研啟動經費（LB2014006）

*通信作者：jwzeng＠xmu.edu.cn

王堅，曾吉文.Brauer特征標的誘導與限制［J］.廈門大學學報：自然科學版，2015，54（4）：502-503.

：Wang Jian，Zeng Jiwen，et al.Induction and restriction of Brauer characters［J］.Journal of Xiamen University：Natural

Science，2015，54（4）：502-503.（in Chinese）