教在兒童學的起點處

查人韻

[摘 要]教學是有起點的，這個起點不只在教材，更在兒童。隨著家庭啟蒙教育、學前教育、社會生活等多種因素的影響，兒童的學習起點越來越個性化和多元化，學習起點的研究得到普遍重視。教在學的起點處，就是要從兒童的“現實起點”出發，把兒童的問題、困惑、經驗、感受等作為材料，在數學學習活動中實現兒童知識、能力、思維、智慧的生長。

[關鍵詞]兒童經驗 教學起點 三角形面積

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2015）11-003

“教學起點”、“學的起點”如今已是教師在各級研修活動中的常用詞之一。“從學的起點出發”的理念，尊重了學習規律，體現了真正的兒童立場。但是學生學習的起點到底在哪，往往需要教師用心“捕捉”，而不是“想當然”。

曾經聽過一節二年級“角的認識”的課。課始，教師讓學生看三個坡度不一的滑梯，讓學生聊一聊最喜歡玩哪個。學生有的說喜歡玩比較“陡”的，刺激，滑得快；有的說比較喜歡玩“平”一點的，安全、平穩。然后教師讓學生思考這三個滑梯里藏著什么數學知識，學生很踴躍地回答，但就是沒人提到“角”。最后教師在畫面上沿著底面畫出一條線，沿著滑梯再畫出一條線，由此引出“角”。

這個案例中，滑梯是生活中常見的玩具，兒童大多也有玩的經驗，滑梯的坡度跟角度有直接的關聯。可是，為什么這個看起來“很生活”“很兒童”“很數學”的東西卻沒能產生很好的學習效果呢？原因很簡單，那就是學生所積累的玩滑梯的經驗并不是和“角”聯系在一起，更多的是活動中的速度、快感、刺激。加上滑梯本身是個物體，而角是一個平面圖形，二者之間的“粘合度”并不是很好，加上教者畫出的角的一條邊是地面，地面并不是滑梯的一個部分。兩個原因疊加，就很容易看出，滑梯未必是學生學習“角”十分恰當的起點。

故而，在教學中，教在兒童學的起點處，不僅很有必要，而且大有文章可做，尤其還要關注不同個體在面對同一學習內容時客觀存在的不同起點。下面以“三角形的面積計算”一課為例，談談我是如何把握學生的學習起點，引領學生一步步完成學習任務的。

一、嘗試探究，找尋起點

課始，讓學生自己想辦法研究圖1中三角形的面積，有困難可以看書。

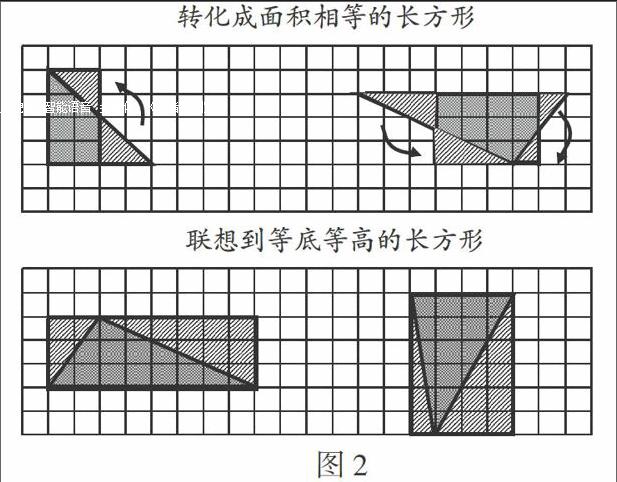
原以為學生會像課本編排的那樣用數格子、轉化成平行四邊形的方法，可結果大大超乎我的想象，僅有少數人用了數格子、轉化成平行四邊形的方法，更多的學生想到了長方形（如圖2）

細細想來，出現這樣的情況是必然的。首先，數格子最大的麻煩就是有很多地方既不是一整格，也不正好是半格，難以產生精確的數據。此外，從知識的角度看，學生的起點是平行四邊形的面積計算，其方法是轉化成面積相等的長方形，因此設法轉化成面積相等的長方形的確是學生的最近發展區。而從三角形聯想到等底等高的長方形，跳出了“等積變形”的局限，具有一定的開拓創新性。

當學生學習的“現實起點”呈現在我面前時，我開始思考：如果從方法的優劣性、普適性的角度，可按數格子、轉化成面積相等的長方形、轉化成等底等高的長方形、轉化成等底等高的平行四邊形的順序，組織學生交流，這樣的學習雖能打開學生的研究視野，但恐怕如蜻蜓點水，學生只是表面理解。我又思考：如果每一種方法都很好，為什么教材只介紹轉化成等底等高的平行四邊形的方法？教師該如何處理好教材與兒童的關系？最終，我決定從兒童的現實起點出發，從多樣化走向最優化。

二、基于起點，展開交流

教材的轉化為平行四邊形的方法是各種方法最優化的結果，也是為后續學習做鋪墊的最重要方法。基于大部分學生都沒有采用轉化成等底等高的平行四邊形面積來算，我認為僅僅停留在個別學生的方法介紹層面是不夠的，必須要讓每個學生親身經歷、積累體驗，使體驗、方法真正轉化成自身的經驗。

生1出示圖3。

師：能介紹一下你的方法嗎？

生1：我是把三角形分成兩個小三角形，左邊的小三角形面積是長為3厘米、寬為2厘米的長方形面積的一半，3×2÷2=3 （平方厘米），右邊的小三角形面積是長為6厘米、寬為3厘米的長方形面積的一半，6×3÷2=9 （平方厘米），9+3=12（平方厘米）。

生2：我也是這樣畫圖的，可是我和他算得不一樣，我是先算出大長方形的面積，然后用大長方形的面積除以2。8×3÷2=12（平方厘米）。

師：看來，計算三角形的面積可以先算算它所在的長方形面積。你能用生3的方法計算下面三角形的面積嗎？（出示圖4）

（學生自主嘗試轉化成等底等高的長方形的方法。為了進一步引導學生掌握這種思路，教師可出示圖5。）

師：觀察兩組圖形和算法，你有什么發現？

生3：算三角形的面積，可以先看成長方形來算，然后除以2就行了，4×5÷2=10（平方厘米）。

師：看成怎樣的長方形來算？

生4：長和寬相當于三角形的底和高。

師：也就是說，每個三角形都可以看成是一個長方形的一半。

三、想象比較，溝通聯系

師（出示圖6）：請大家大膽想象，這個三角形，還可以看成是什么圖形的一半呢？

（學生交流自己的想法后，教師出示圖7）

生1：這時的三角形面積是平行四邊形的一半。

師：能借助平行四邊形面積的計算推算出這個三角形面積嗎？

生2：4×5÷2=10（平方厘米）。

生3：跟剛才的算式一樣呢。

師：比較圖5和圖7，有什么發現？

生4：三角形的面積都占了一半。

生5：長方形面積和平行四邊形面積相等，都是用4×5。

師：也就是說，把三角形轉化成等底等高的平行四邊形或長方形，三角形的面積是平行四邊形或長方形面積的——一半。

師（再次出示圖3）：如果將這個三角形也看成是一個平行四邊形的一半，這個平行四邊形是什么樣子呢？你能用兩個同樣的三角形來演示一下嗎？

學生操作演示多種不同的拼法，但是，不管怎么拼，三角形的面積都是平行四邊形面積的一半，計算面積也可以用8×3÷2=12（平方厘米）計算。

從學生比較容易理解的方法出發，讓學生在講述和交流中逐步感受到每個三角形都可以看成是它所在的長方形或平行四邊形的一半，只要算出長方形或平行四邊形面積即可。

讓學生獨立填寫表格。

我發現： 。

這一環節，讓學生離開直觀圖形，進入純運算階段（也可以結合想象），讓學生牢固掌握之前研究出的三角形面積計算的方法（底×高÷2）。

四、科學解釋，提升認識

師（出示圖8）：我發現有的同學也由三角形想到了長方形，但并不是我們剛才研究的方法。這樣的轉化可以算出三角形面積嗎？先看左邊的三角形。

生1：左邊三角形的面積是4×2=8（平方厘米）。

師：4是三角形的——底，2是三角形的——高的一半。也就是用底乘以——

生2：底ד高÷2”。（板書“底×高÷2”）

師：右邊三角形的面積呢？

生3：右邊三角形的面積是4×3=8（平方厘米）。

師：如果用底和高來說呢？

生4：高×底÷2。（板書“高×底÷2”）

師：比較“底×高÷2”、“底×高÷2”、“高×底÷2”，有什么發現？

生5：其實是一樣的，都是底和高相乘再除以2。

師：是啊，條條大路通羅馬，看起來你們研究的方法不一樣，但是經過研究，可以發現它們其實是相通的。數學就是這樣神奇而有趣。

……

可見，“教在兒童學的起點處”，并不只是說學習的開始，也包括學習的全程。此外，教師的引導，不僅讓學生感受到思維的多樣化，還能讓學生體會到多樣性中的統一性和最優性。

（責編 金 鈴）