數學課例題功能的解析及其教學實施

劉靜

例題教學是數學教學的重要組成部分。對例題的功能解析和例題的教學進行了深刻的闡述，認為可以通過“研讀教學內容，確定目標指向；明確例題功能，助力目標落實；實施例題教學，凸顯例題功能”等步驟具體從應用示范、深化理解、解題分析示范、數學表達示范、數學精神體驗等方面解析例題功能，經歷“理解題意、擬定計劃、實施計劃、回顧反思”等過程實施例題教學。

數學例題例題功能例題教學一、數學課例題功能解析中的問題

數學教學離不開例題教學。例題作為數學教學的重要內容，它蘊含的功能不可忽視。然而目前關于例題教學還存在著許多問題：

1.快餐。課堂容量過大，不講究細嚼慢咽，大口大口吞食“例題”。教師急于知識的灌輸，僅以學生“知道”為目的，對例題的答案過分追求，忽視過程，寄希望于重復的機械操練。因此學生在“知道”后又被迫于大量做題，憑借自己有限的解題經驗進行簡單重復的解題實踐，超量訓練讓學生也學會了“快餐式”學習，惡性循環，致使學生學習負擔很重且學習效率低。

2.割裂。忽視數學內容、方法的聯系性。教師在進行例題教學設計時，只顧眼前，有意或無意地割裂了數學知識，致使學生頭腦中的數學知識或方法失去生命力，體系紊亂。

3.包辦。忽視學生的主體地位。在例題教學時，教師以自己的經驗替代學生的經驗，將自己對例題的認識強加與學生，在過程中，以例題分析時替代學生理解、概括，使例題教學無效。

如何發揮例題教學的最大效能，已成為當今促進數學課堂教學改革的一個至關重要的問題。筆者對數學例題教學試圖尋求一種操作可行、有效的例題教育功能解析和教學方法。

二、例題的功能解析概念界定

例題的功能具有“學術”和“教育”雙重性。就“學術形態”的數學本身而言，它具有本體的數學功能，就“教育形態”的數學教學而言，它具有介質的教育功能，是幫助學生認識數學，幫助學生體驗數學的過程和幫助學生提升學習數學的情感、態度和價值觀的介質。學生通過例題學習，學會舉一反三，聯系或深化知識，推廣方法，感悟數學思想，積累數學化的經驗。例題功能的解析就是具體分析例題及其教學在相應教學內容中的知識、方法、經驗，情感上對教學目標達成所起到的作用。通過相對準確的“例題的功能解析”，利于指導例題教學，提高教學效益。

三、例題的功能解析及教學的實踐

例題教學從例題的功能解析開始。下面以浙教版教材七年級上冊《6.8余角和補角》節例1為例具體說明如何解析例題的功能、如何開展例題教學。

（一）研讀教學內容，確定目標指向

首先，從教材看。本章內容是初中幾何的開始，也是從圖形簡單認識到深入研究的一次飛躍，是后續知識的基礎；本章從現實世界抽象出幾何圖形開始，再具體地呈現線段、直線、射線和角的概念、表示法和畫法以及線段和差、角的和差、直線關系等，本節內容涉及余角和補角的概念和性質。就數學體系而言，（1）概念體系：角的概念是通過射線來建立的，余角、補角則在角的和差概念基礎上生成，而角的和差涉及數與形的統一，后續教材中大量存在數形統一轉化的方法來進行計算證明的內容。（2）公理化體系：本章是演繹表述的開始。

其次，分析本節課期望達到的廣度和深度。通過上述對這節課的內容進行分析，可以認識到平面幾何知識板塊之間的相互聯系，進一步可以明確：余角、補角的學習，需要讓學生體會到數與形的統一，通過數形轉化可以進行說理計算，得到讓人信服的結果；同時要讓學生體驗到“怎樣說明，才讓人信服”。也就是后續的演繹證明。

再次，確定教學目標。根據課程標準中關于注重課程目標整體實現的要求，每節課的教學目標都可以具體化，有些隱性有些顯性，有些則是長期教學過程中的一個點，但這些目標往往互相關聯。因此在確定目標時重點應明確，忌本末倒置。可以綜合課程標準，內容分析，以及學生情況最終確定教學目標。本章是初中階段的幾何起始內容，學生對幾何概念學習和性質探索比較陌生，尤其是說理的分析和表述。因此確定重點目標是：（1）經歷補角和余角概念的發生過程，認識余角補角；（2）經歷余角補角性質的探索過程，理解并會應用性質；（3）體驗說理的過程，積累說理表達的經驗。感悟數形結合思想。

（二）明確例題功能，助力目標落實

七下教材第164頁《6.8余角和補角》例1：

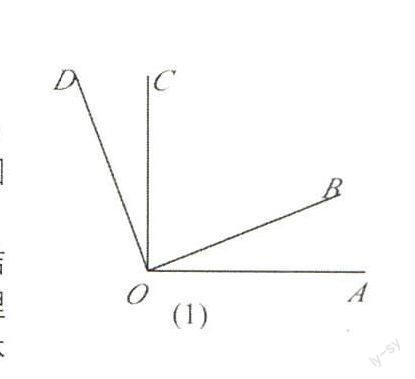
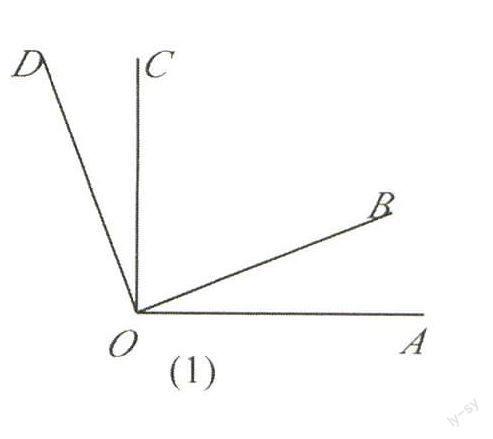
如圖1，已知∠AOC=∠BOD=Rt∠指出圖中還有哪些角相等，并說明理由。

根據所在例題章節內容，圍繞教學目標，結合具體的例題內容從例題的應用示范、深化理解、解題分析示范、數學表達示范、數學精神體驗等方面功能進行解析。

1.知識應用示范。教材編排時將這一例題在兩條性質“同角或等角的余角相等”“同角或等角的補角相等”之后呈現。因此該例是對性質“同角或等角的余角相等”的及時應用。這里找到的角相等正是以“同角的余角相等”為依據的，通過在具體的問題中運用這一性質，使學生對知識的理解更具體、更深刻，達到落實本節課關于性質的理解和應用目標的目的。

2.知識深化理解。該例還涉及本節課互余的概念，在新的情境中辨認互余，鞏固對互余的認識。條件中沒有直接給出互余的條件，而是以等價條件“∠AOC=∠BOD=Rt∠”間接告知，學生在審題時需要對條件進行加工，這個過程是對本節課目標“互余的認識”的深化。

3.解題分析示范。例題要求尋找相等的角，并且說明理由，對于初學者來說并不簡單，這是幾何計算和證明初級階段，根據之前的分析可以知道，后面涉及了大量的問題需要學生有“如何分析一個問題”的經驗。綜合法和分析法是常用的分析方法，這里通過例題就可以給學生以“分析問題，形成思路”的過程性示范，以達到提升分析和解決問題能力、發展合情推理和演繹推理能力、積累數學活動經驗等目的。

4.數學表達示范。在學習分析，形成思路后，為了方便交流，需要有讓人看得明白并值得信賴的說理表達。這一例正是說理表達學習的開始，學生通過經歷口頭說理，書面表達，示范參考等過程，不斷完善說理表達，為演繹證明打下基礎。因此該例可助力于學會數學推理、清晰表達等目標的落實。

5.數學精神體驗。說理需要步步有據，通過找到相等的角后，再說說理由，體現了數學的嚴謹性。學生經歷了例題從分析到解決的過程，就能體會到數學的這一特點，長期的體驗，最終能促使他們形成科學的態度。通過對例題學習的回顧反思，讓學生體驗反思的好處，示范“可以如何反思”，以落實關于“初步形成評價與反思意識”的課程目標。

例題的功能解析形成需要教師先宏觀把握整體教學內容，確定教學的具體目標，再圍繞教學目標從例題的應用示范、深化理解、解題分析示范、數學表達示范、數學精神體驗等方面功能進行解析。

（三）實施例題教學，凸顯例題功能

對例題功能的解析目的在于更好的實施例題教學。筆者在實踐中進行了一些嘗試，認為例題教學可以圍繞波利亞《怎樣解題》的四個步驟展開。下面以上述例題作具體說明。在兩條性質之后呈現例題的題目：

如圖1，已知∠AOC=∠BOD=Rt∠指出圖中還有那些角相等，并說明理由。

1.理解題目：①學生審題，在圖形中標注直角符號。②回溯（回到已有的知識方法或經驗）：問題是什么，對找相等的角，你有什么經驗？條件是什么？由條件可以獲得哪些結論？

數學學習是一個再創造的過程，學生需要從他頭腦中調取已有的知識方法，進行加工創造。因此在例題教學時，需要先喚醒那部分已有的知識方法或經驗，即例題回溯。在這個例題回溯中，教師是跳出例題本身，引導學生回憶以往找相等角的經驗（角平分線），以及從條件“∠AOC=∠BOD=Rt∠”獲得的結論回憶直角、互余等知識，使該例在“深化互余概念認識”上的功能得以發揮。

2.擬定計劃：①說說回溯中的問題，同時教師板書學生說的“找角相等的經驗”“由條件得到的結論”。②你覺得你的經驗能幫助你在這里找到相等的角嗎？在由條件得到的結論中你對找相等的角有用嗎？

這里將回溯環節獲得的已有知識方法或經驗進行刪選加工，以縮小條件和結論的距離。在這個過程中學生需要激活剛剛獲得的性質“同角的余角相等”，這正是條件和結論的連接點。通過上述引導自然地用“同角的余角相等”來連接例題的條件和結論，本例題在“知識應用示范”和“解題分析示范”上的功能就得以發揮了。

3.執行計劃：①你找到相等的角了嗎？你能說明理由嗎？說給同學聽一聽。②請學生口述，教師進行規范的解題板書。

該例作為幾何說理的開始，通過學生自己說說，和同學說說，教師矯正并進行仔細規范的板書示范，不斷完善學生的說理表達，發展數學表達能力，同時也體驗到了數學的嚴謹性。這一過程充分發揮了該例題在“數學表達示范”上的功能。

4.回顧反思。回顧整個例題解決的過程，這里用到了哪些知識？是怎么分析的？你對你的結論確信嗎？

解出例題不是教學的目的，例題作為現成的數學，教材中更給出了答案。因此在解完一個題之后及時的回顧反思是非常必要的。上述對例題“用到了哪些知識”是對所學知識的一次回顧；“是怎么分析的？”是通過對解題過程的回顧再一次學習“如何解題”，積累分析問題的經驗；“你對你的結論確信嗎？”又是對演繹的一次認識，對“怎么說理？”的更清晰的認識。提升反思意識是本學段教學的目標之一，該例題的教學在“數學精神體驗”之“學習反思”上的功能就由上述環節體現，同時該回顧反思的過程還是例題“應用示范、深化理解、解題分析示范、數學表達示范、數學精神體驗”等方面功能的升華。值得說明的是反思的形式可以多樣化，如反思表、交流形式、教師點撥等，同時反思意識的培養需要一個長期持續的指導，因此在例題教學的反思環節應該根據例題的功能結合不同的階段循序漸進地進行。

四、結束語

綜上所述，例題是教學內容的重要組成部分。作為數學教育的一線教師只有理解例題配置的目的，解析例題的功能才能有方向地進行例題教學。在例題教學中可以從“研讀教學內容，確定目標指向”、“明確例題功能，助力目標落實”、“實施例題教學，凸顯例題功能”三個步驟完成例題在“應用示范、深化理解、解題分析示范、數學表達示范、數學精神體驗”等方面的功能解析，經歷“理解題意、擬定計劃、實施計劃、回顧反思”等過程實施例題教學。例題的功能解析不僅可以幫助理解教材設置該例的目的，指導例題教學，也是例題改編或替換的依據。

參考文獻：

[1]弗賴登塔爾.作為教育任務的數學.上海教育出版社.

[2]教育部.數學課程標準.北京師范大學出版社，2011.

[3]波利亞.怎樣解題.上海科技教育出版社.