分析學生錯解心理 創設最佳矯正情境

王立琴

【摘 要】 教師隨時分析學生的解題心理，并通過“心理換位”來研究形成學生學習障礙的原因，尋求合適的啟發角度，幫助不同層次的學生獲得不同層次的成功，排除影響學生解題心理障礙，這既是提高學生分析問題能力的需要，更是從應試教育向素質教育轉化的需要。

【關 鍵 詞】 解題心理；教學；數學

在數學教學中，解題對于發展認識結構，增強數學思維能力，培養創造精神起著重要作用。因為在教學過程中，雖然可以通過分層教學，調動不同層次的學生的學習積極性和主動性，但對于教學對象的個別差異和客觀性，學生在理解知識、掌握技能和解題方法等方面往往存在“缺陷”，這除了數學基本知識外，更主要的原因在于心理因素。因此，在教學過程中，教師應重視解題錯誤的心理分析，創設矯正情境，及時矯正學生學習心理上的缺陷。

一、片面理解題設條件而改錯

由于學生邏輯思維不夠嚴密，在審題主要是分析題設條件時，易受題設的互相干擾和抑制的影響，常常出現按照自己期望和經驗補充或修改題設條件的心理傾向。因此解題時，常作一些潛在的假設。

例1：如圖1所示，O0的半徑為5厘米，弦AB∥CD，AB=6厘米，CD=8厘米，求AB和CD的距離。

錯解：如圖2所示，作OE垂直CD，交AB于F利用RT△OEA和RT△OFC分別求出OE、OF，則所求AB、CD間的距離為EO-OF=1或OE+OF=7，學生按照自己的需求與期望理解設題設時，對弦AB、CD的位置進行了規定，作出了潛在的假設AB、CD在圓心O的同側或兩側，而忽視了位置的多樣性，造成遺漏一個答案。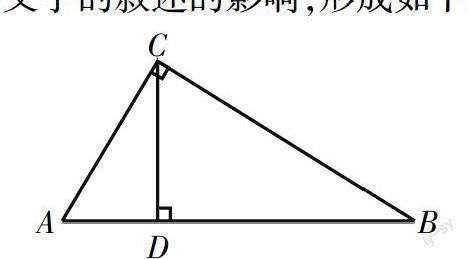

因此，教師在對學生進行數形結合這一數學思想培養和直觀教學時，要培養學生在不同情境中掌握概念的本質并通過學生討論、分析、使用，在其產生的錯誤結論中建立正確認識，提高綜合判斷能力。

二、思維定式的影響

思維定勢指的是一種思維慣性，中學生的思維處于邏輯抽象的經驗型向理論型發展，思維品質的獨立性與全面性交錯發展的時期。因此，積累一定的解題經驗是必要的。但是大部分學生在此基礎上解題時常常首先對新問題進行模式辨認，也就是聯想、比較、歸類，這就有無意識地把相似的新問題納入到已建立的模式中加以解決的心理傾向，總想用在以前掌握的舊知識的基礎上的方法解決問題，這就使所學的新知識、新方法得不到應用，因此，解題過程就非常繁瑣，有時甚至無中生有，自家條件。

例2：已知：RT△ABC中∠C=90°，AC=3，BC=4，求斜邊AB邊上的高，如圖在解這道題時，一般學生易受圖形和文字的敘述的影響，形成如下思維定式：

由點C向AB作垂線段為CD，然后，利用與直角三角形有關的射影定理或勾股定理求出CD。

此解法之繁是思維定式產生的“呆板性”造成的，以為直角三角形的問題非用勾股定理不可。其實利用三角形面積公式，很快就能計算出來。

克服學生這種思維定“死”或思維惰性的有效方法是：創設不同的情境，培養他們積極思維，養成認真審題，從不同角度、不同方面對問題進行認真分析的習慣，并采用變式、對比、改正錯誤和強調前提條件等方式來進行針對性教學，培養學生發散性思維和逆向思維的能力。（下轉13頁）

（上接11頁）

三、求易心理，忽視隱含條件

學生的解題過程就是對題設信息的刺激不斷做出反應，以求得解題途徑及解題方法的過程，由于求易心理的影響，對于一些較簡單的問題，學生由于憑借直觀能夠得到的解題方法，往往有放棄嚴密邏輯論證的心理傾向。

例3：當m為何值時，方程（m-1）x2-（2m-1）x+（m+1）=0有相異實根？

在解決此問題時學生很容易由Δ>0，求得m<，遺漏m-1=0的條件而落入陷阱。

這種情況往往是由于對于某一概念有意義或本身存在的條件不清楚、不熟悉造成的。因此，在教學過程中，教師不應忽略對概念中隱含條件的分析，要反復強調，并不時給出一些相應的問題讓學生進行討論、分析、解決，以引起學生注意并記憶。

四、解題心理與情緒

心理學的研究表明，情緒與解決問題有密切關系，焦慮程度與學習成績的關系呈倒V 型曲線，即適中的焦慮程度有助于問題的解決，而焦慮程度過高或過低均不能表現出良好的解題能力。

學生的解題過程是一個不斷嘗試解題途徑的過程，一旦不能很快找到正確的解題方法，就會產生焦慮心理，過度的焦慮會使人產生高度注意定向而強化思維定式，即只注意了解題方法而忽略了題設與題設之間，題設與結論之間的本質聯系，從而沖淡了學生的記憶，產生暫時的遺忘，于是公式、定理的前提條件甚至平時熟知的“分母不為零”等常識性知識也會隨著嘗試的深入和高度注意定向而被暫時遺忘，忽視對解題時所用手段的必要檢查。因此，平時給學生的壓力要適度，特別是在會考前，應盡量從各種因素及各個方面給學生松綁減壓，使他們的心理情緒在臨考前能調節到最佳狀態。

綜上所述，教師隨時分析學生的解題心理，并通過“心理換位”來研究形成學生學習障礙的原因，尋求合適的啟發角度，幫助不同層次的學生獲得不同層次的成功，排除影響學生解題的心理障礙，這既是提高學生分析問題能力的需要，更是從應試教育向素質教育轉化的需要。

【參考文獻】

[1] 趙玉杰. 淺議中學生數學素養的培養[J]. 新一代，2015（2）.

[2] 王志剛. 影響高中生數學解題的心理分析及干預策略[J]. 中學生數理化（學研版），2015（3）.

[3] 王玄化. 突破數學解題心理誤區[J]. 高中數理化，2011（Z2）.