“認識三角形和四邊形”復習指導

邱廷建

一、整理復習知識

1 三角形的特性

用3根小棒擺三角形，無論怎樣擺，擺出的三角形的形狀和大小都是一樣的，說明三角形具有穩定性。用4根同樣長的小棒擺四邊形，則可以擺出形狀、大小不同的四邊形，說明四邊形容易變形。

2 三角形的分類

三角形按角分可以分為三類：銳角三角形、直角三角形和鈍角三角形。三個角都是銳角的三角形叫做銳角三角形。有一個角是直角的三角形叫做直角三角形。有一個角是鈍角的三角形叫做鈍角三角形。

三角形按邊分可以分為不等邊三角形和等腰三角形。等腰三角形又包含等邊三角形。兩條邊相等的三角形叫做等腰三角形。三條邊都相等的三角形叫做等邊三角形。等邊三角形每個角都是60°。

3 三角形的內角和

把一個三角形的三個角剪下來，可以拼成一個平角，因此三角形的內角和是180°。四邊形可以分成兩個三角形，因此四邊形的內角和是360°。

4 三角形三邊的關系

三角形任意兩邊的和大于第三邊。可以根據三角形三邊的關系，來判斷三條線段能否圍成一個三角形。

5 四邊形的分類

有兩組對邊分別平行的四邊形是平行四邊形。只有一組對邊平行的四邊形是梯形。正方形、長方形是特殊的平行四邊形。正方形是特殊的長方形。正方形、長方形、平行四邊形之間的關系可以用下面的圖來表示：

二、解題指導

例1 在一個三角形中，其中兩個角的度數是120°、25°，求另一個角的度數。

[分析與解]因為三角形的三個內角和是180°，所以用180°分別減去120°和25°，就是另一個角的度數。列式計算：180°-120°-25°=35°。

例2 下面的三角形只露出一個角，猜一猜，它是什么三角形？

[分析與解】三角形按角分，可分為銳角三角形、直角三角形和鈍角三角形三類。任何一個三角形至少有兩個銳角，如果三角形其中的一個角是銳角，那么其他兩個角可能都是銳角，也可能是銳角和直角，還可能是銳角和鈍角。題中的三角形只露出一個角，遮蓋了兩個角，這兩個角就可能是銳角和銳角，也可能是銳角和直角，還可能是銳角和鈍角。因此，這個三角形可能是銳角三角形，也可能是直角三角形，還可能是鈍角三角形。所以這道題無法準確判斷是什么三角形。

例3 用長分別是5厘米、7厘米和10厘米的三根小棒，能擺成一個三角形嗎？

[分析與解]可以根據“三角形三邊的關系——三角形任意兩邊的和大于第三邊”來判斷，先算出任意兩邊的和，再與第三邊比較。因為5+7>10，5+10>7，7+10>5，說明任意兩邊的和大于第三邊，所以用長分別是5厘米、7厘米和10厘米的三根小棒，能擺成一個三角形。當然，還有更簡便的判斷方法，就是用較短的兩邊之和與最長邊比較，如果較短的兩邊之和大于最長邊，就能擺成一個三角形。因為5+7>10，所以用長分別是5厘米、7厘米和10厘米的三根小棒，能擺成一個三角形。

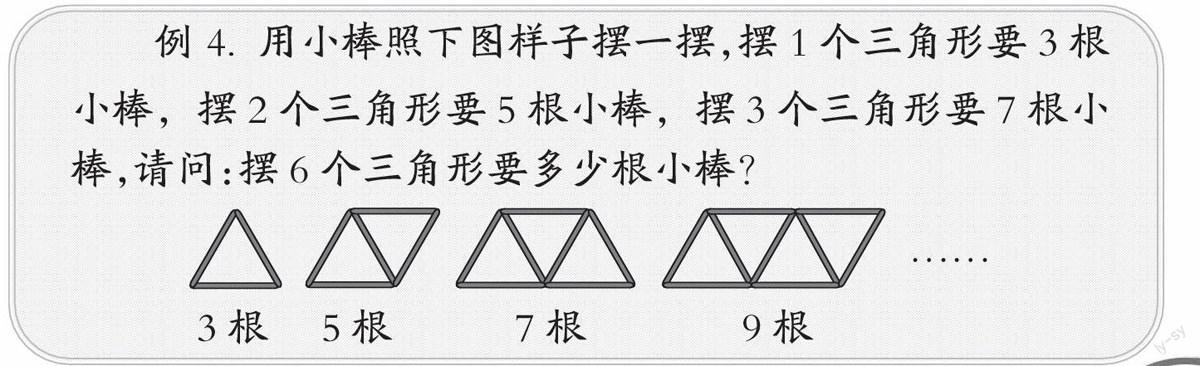
例4 用小棒照下圖樣子擺一擺，擺1個三角形要3根小棒，擺2個三角形要5根小棒，擺3個三角形要7根小棒，請問：擺6個三角形要多少根小棒？

[分析與解]可以照樣子用小棒接著擺一擺，擺4個三角形要9根小棒，擺5個三角形要11根小棒，擺6個三角形要13根小棒。也可以這樣想：從第2個圖形開始，每增加1個三角形只要增加2根小棒（可以利用原來三角形其中的1根小棒作邊），也就是說，第2個圖形增加1個2根小棒，第3個圖形增加2個2根小棒，第4個圖形增加3個2根小棒，第5個圖形增加4個2根小棒，第6個圖形增加5個2根小棒，因此擺6個三角形需要的小棒數量是：3+5×2=13（根）。由此我們可以得出一個計算公式：擺n個三角形需要的小棒數量=3+（n-1）×2。

（本文作者為福建省上杭縣教師進修學校特級教師）