展示中學數學“化歸思想”神奇魅力
余祚鑒
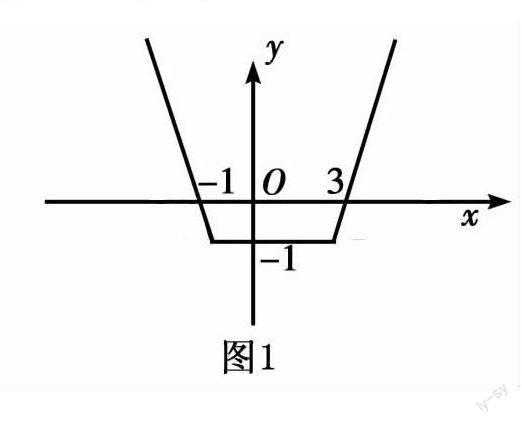
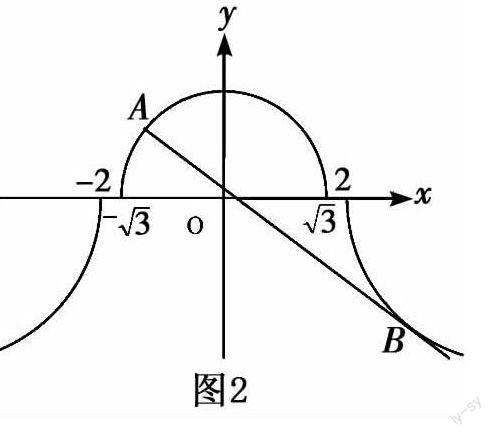

摘 要:什么是數學化歸思想?——通過仔細觀察、合理分析、展開聯想、運用類比等一系列數學思維過程,把數學中暫時不能解決的問題,通過選擇恰當的方式方法進行轉化,歸結到一個或一些已經掌握或能夠解決的問題,進而能夠輕松解決原問題的這種解決問題的思維方式叫做化歸思想 [1 ].培養化歸方法之前要真正了解化歸思想的內涵和總的目標方向,比如往熟悉化、簡單化、具體化等目標方向轉化.中學數學中常用的化歸法主要有:函數-方程-不等式轉化、化整為零式的轉化、正反轉化、等與不等的轉化、動靜轉化、數形轉化等.
關鍵詞:化歸思想;數學教學;化歸轉化方向;應用劃歸思想解題
引言
素質教育與新課程改革中均提出“教學的任務除了向學生傳授系統的基礎知識和基本技能,還應發展學生的智力、體力、和創造才能”.這里強調的創造才能就是指要培養學生們善于、習慣于運用已有的知識儲備和智能去探索、發現和掌握未知領域的知識的重要能力.在數學學科中化歸思想無疑是發揮學生的創造才能以達到解決數學問題的重要思想方法之一.前蘇聯教育家維果斯基的“最近發展區”學習理論有著異曲同工之妙處,該理論中學生的已有發展水平和未來的發展水平之間的差距叫做最近發展區,在數學中如何從“已有發展水平”過渡到“未來的發展水平”呢 [2 ]?數學化歸方法在這方面剛好可以起到很好的踏板和過渡作用.努力將這一重要數學思想貫穿于整個數學教學中,鼓勵學生掌握這一思想方法,并學會用它分析、處理和解決問題.俗話說得好,授之以魚,不如授之以漁.在數學教學中應高度重視中學數學中的方程思想、數形結合思想、化歸思想、數學模型思想、分類與歸納思想等這些數學學科領域的思維方式和方法論,掌握這些數學思想的教學技能是一名數學教師必備的學科專業素養,它也符合新課程改革的理念,而化歸思想是中學數學中重要的邏輯思維方式和方法論之一.結合本人十幾年的一線教學實踐,筆者就化歸思想的基本內涵、如何應用化歸方法解題及應注意的一些地方提出幾點認識.
1 掌握和應用化歸思想方法的總體方向與目標:
運用這種數學思想方法時首先要確定化歸的方向和目標.化歸過程要善于展開豐富的聯想能力,當遇到一些陌生的問題時,應從自己大腦知識題庫中去聯想、搜索查找有無與這一問題較類似的知識儲備(可以從條件、結論、提法、形式、圖形等各方面聯想),從不熟悉中尋找到似曾相識的感覺,并以此為突破口,找到打開這把鎖的鑰匙,學生害怕數學的原因大都是恐懼遇上沒見過或沒做過的題目和問題,一旦找到解題方向也就可以將原問題進行轉化,或利用已經掌握的解題思路確定化歸的方向.
例1(2011年高考福建文科數學卷第16題)商家通常依據“樂觀系數準則”確定商品銷售價格,即根據商品的最低銷售限價a,最高銷售限價b(b>a)以及實數x(0 化歸的思想廣泛應用于數學的研究和學習之中,教師應十分重視這種方法在數學教學中的運用,由此對提高學生思維的靈活性,廣闊性,敏捷性,創造性及發現問題,探索問題,解決問題的能力將產生重要的意義.同時必須明確化歸方法也不是“萬金油”式的無所不能的金鑰匙,化歸思想的應用關鍵在于方向性,足夠的數學知識儲備和科學思維方法為發揮化歸方法提供了可能性.因此化歸方法在具有一定的數學認知結構的基礎上,結合應用其它的數學思維方式和方法定會在數學領域里如魚得水. 參考文獻: [1]王子興.數學方法論[M].北京:高等教育出版社出版,1998. [2]張廣祥.中學代數研究[M].北京:高等教育出版社.2006.

