歐拉積分性質及應用
盧路加 張君會 趙志穩
歐拉積分性質及應用
盧路加 張君會 趙志穩
現在我們很多時候解決問題的工具還是初等函數,這給我們的一些研究帶來了很多不便。含參量積分是解決問題的另一重要工具,同時含參變量積分也是引進非初等函數,構造新函數的一個重要途徑,歐拉積分就是在應用中經常出現的含參量積分表示的函數,它雖身為含參量積分的一種特例,但本身也是許多積分的抽象概括,能為相關積分的計算帶來方便。歐拉積分在理論和實踐上的地位僅次于初等函數,應用十分廣泛。
含參量積分;歐拉積分;性質;應用
一、歐拉積分的基本知識
(一)Γ函數的性質
1.定義域:Γ函數在s>0時收斂,即定義域為s>0.
2.連續性:在任何閉區間[a,b](a>0)上一致收斂,所以Γ(s)在s>0上連續。
3.可微性:
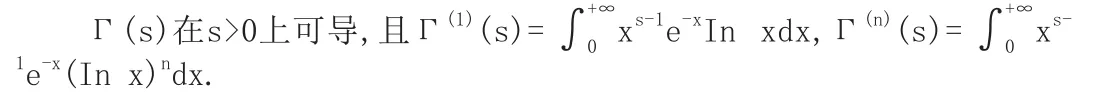
4.遞推公式:Γ(s+1)若s為正整數n,則Γ(n+1)=n!
5.Γ(s)的其他形式:
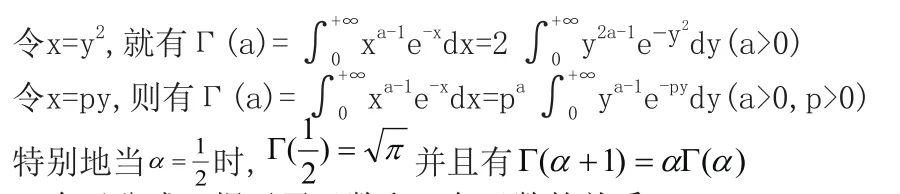
6.余元公式:揭示了函數和三角函數的關系
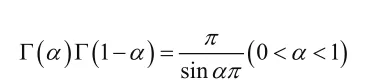
7.倍元公式:
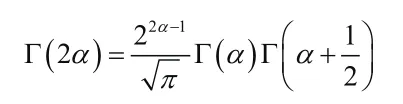
(二)B函數的性質
1.定義域:B(p,q)的定義域為p>0,q>0.
2.連續性:B(p,q)在p>0,q>0內連續.
3.對稱性:B(p,q)=B(q,p)
4.遞推公式:

(三)Γ函數與B函數之間的關系
二、歐拉積分的應用
通過式子的變形將積分變成歐拉積分的形式,也可以利用換元法將未知積分化為歐拉積分,再利用歐拉積分的相關性質,計算出該積分的值。
(一)應用一直接將積分變成歐拉積分
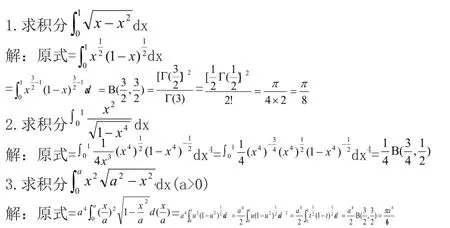
(二)應用二利用換元法將未知積分化為歐拉積分

應用三歐拉積分性質的應用(1)
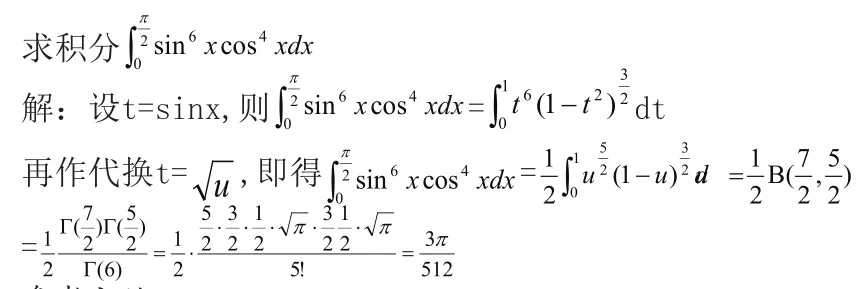
[1]華東師范大學數學系,《數學分析》[M],(上,下冊)北京:高等教育出版社,2007.
[2]裴禮文.數學分析中的典型問題與方法[M].北京:高等教育出版社,1993.
[3]費定輝,周學圣等,吉米多維奇數學分析習題集題解(五)[M],濟南:山東科學技術出版社,1999.
[4]錢吉林.數學分析題解精粹[M].崇文書局,2003.
(作者單位:河南師范大學)
盧路加(1993—),男,漢,河南省周口市,本科學歷,河南師范大學。
張君會(1995—),男,漢,河南省濮陽市,本科學歷,河南師范大學。
趙志穩(1993—),男,漢,河南省安陽市,本科學歷,河南師范大學。

