箭載GPS定位臨近地面衛星對流層延遲改正模型

饒愛水，李清梅，胡 健，吳關鵬

（中國衛星海上測控部，江陰 214431）

箭載GPS定位臨近地面衛星對流層延遲改正模型

饒愛水，李清梅，胡 健，吳關鵬

（中國衛星海上測控部，江陰 214431）

針對經典對流層延遲改正模型無法處理負仰角衛星誤差修正的問題，在傳統球對稱標準大氣模型的基礎上，采用射線描跡法建立了GPS信號穿透對流層的數學模型，推導了根據對流層折射最低點海拔高度計算對流層延遲改正的計算公式；為求解對流層折射最低點海拔高度，采用最小二乘法求得 GPS信號穿透對流層時地心張角與最低點海拔高度之間的線性方程，提出了根據衛星和火箭之間的夾角與地心張角之間的關系進行迭代計算，進而求得最低點海拔高度的方法；最后引入了模型誤差因子，評估對流層延遲改正模型的效果。采用火箭飛行試驗數據對模型進行驗證，結果表明，該模型提供的方法能夠消除負仰角衛星大部分對流層延遲，消除的最大延遲可達135 m，消除對流層延遲后的臨近地面衛星參與定位計算使最終定位精度提高25 m，計算迭代次數平均10次，尤其適合箭載GPS實時定位。

折射指數；折射率；地心張角；射線描跡；大氣折射

經典的對流層延遲改正模型包括Hopfield模型、Saastamoinen模型、Black模型等直接計算模型，也包括CFA模型、Chao模型、Niell模型等利用映射函數計算模型[1]，適用于仰角大于5°的情況，部分文獻研究了在仰角在0°和5°之間的對流層改正模型[2]，網絡差分對流層誤差內插模型也被大量研究[3]，但對于負仰角的對流層延遲改正尚缺乏研究。運載火箭飛行高度通常超過對流層最大高度（60 km），對于仰角大于0°的衛星，對流層延遲改正為0 m；對于仰角小于0°且貼近地面的衛星，由于無線電波穿透整個對流層，對流層延遲改正數可達上百米。貼近地面衛星對最終定位結果的精度影響很大，采用衛星動態遮蔽角[4]可有效屏蔽貼近地面衛星對定位結果的影響，但減少了參與定位衛星個數。本文基于射線描跡法[5-6]，研究了GPS信號穿透對流層時的延遲改正模型，提出了根據對流層折射最低點海拔高度計算延遲改正的方法。

1 對流層穿透大氣折射模型

在球對稱的大氣模型下，采用射線描跡法，考慮貼近地面衛星信號穿透對流層進入箭載GPS接收機的情況。圖1把大氣示意為兩層，GPS衛星從G點發出無線電波，在A′2點進入大氣層，經過大氣折射最低點A0，從A1點進入第2層大氣，大氣層外緣A2點穿出，進入位于R點的接收機。A0、A1、A2點距離地心的距離分別為r0、r1、r2，在A1、A2點的大氣入射角分別為z1、z2,對應的出射角分別為z′1、z′2，[A0, A1）、[A1，A2）之間的大氣折射指數分為n1（A0點的折射指數）、n2（A1點的折射指數），A0A1、A1A2的長度分別為l1、l2，對應的地心張角分別為c1、c2。根據Snell定律[7]，有：

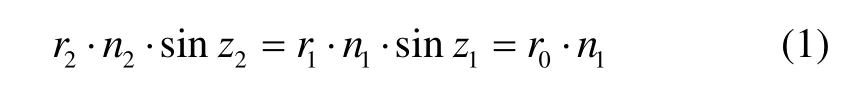
在△OA1A2中，

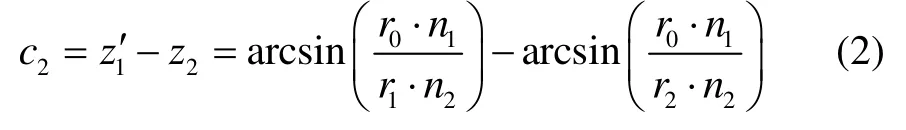
對應的折線長度為

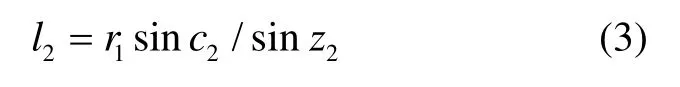
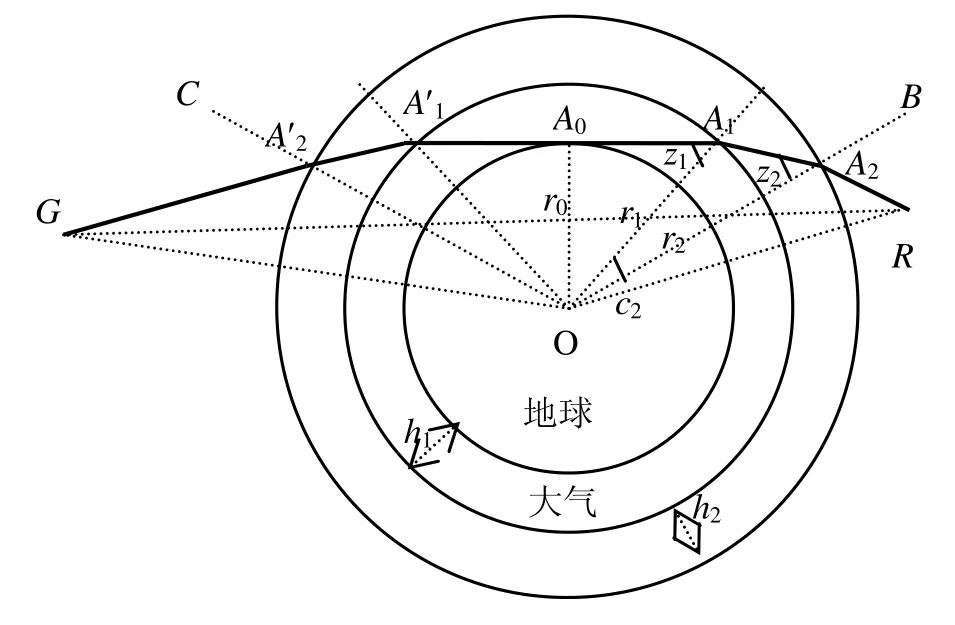
圖 1 箭載GPS信號穿透對流層示意圖Fig.1 On-board GPS signals penetrate through troposphere

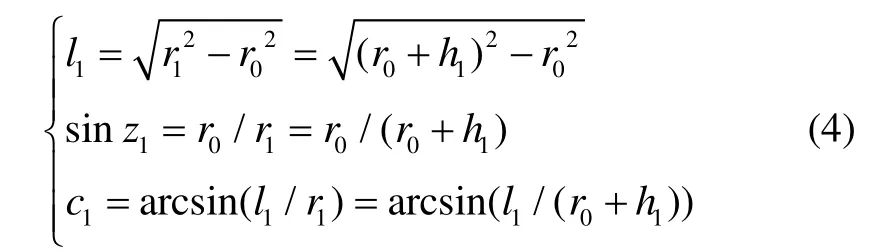
當大氣被劃分為m層時(2≤ i≤m )，有：

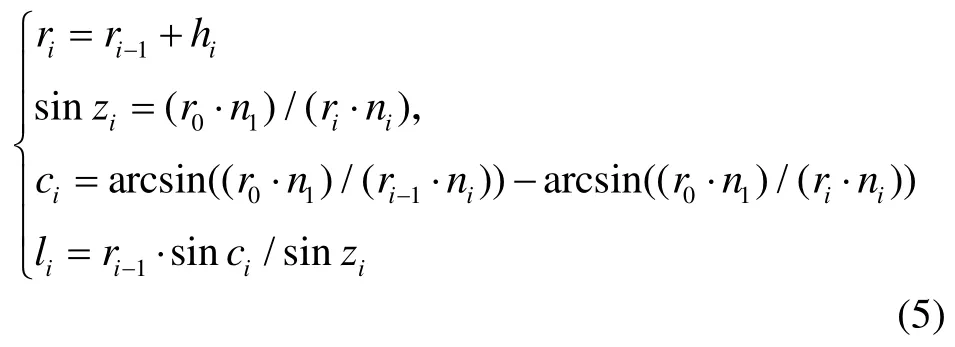
定義Vtrop為對流層延遲，根據對流層延遲計算公式[1]，有：

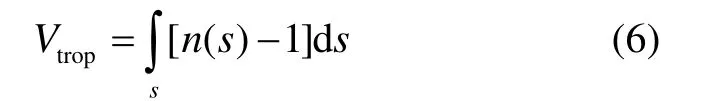
式中，S為電磁波在大氣中傳輸的路徑，n(s)為路徑上的大氣折射指數。在球對稱的m層大氣模型下，上式可近似為

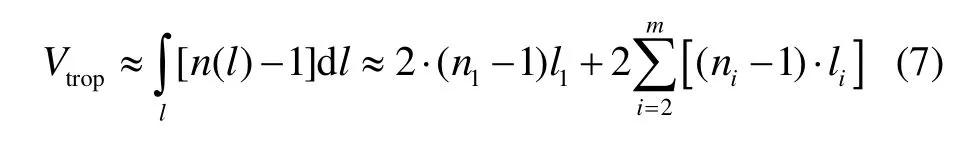
路徑S對應的地心張角Cs為

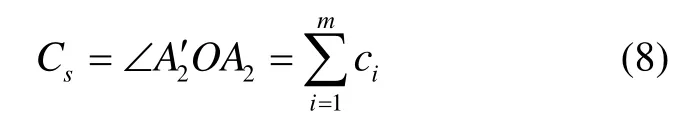
2 對流層延遲計算

根據大氣折射率計算公式[7]：

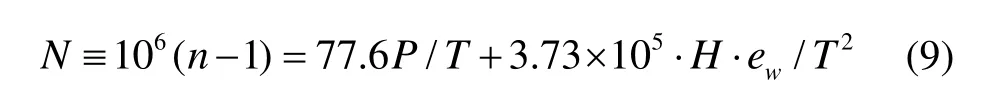
式中，

其中：h為大氣的海拔高度，單位m；P為大氣氣壓，單位為100 N/m2；T為大氣絕對溫度，單位K；t為大氣溫度，單位℃。本文采用ICAO（國際民航組織）標準大氣模型[8-9]計算大氣壓力和溫度，得到的大氣折射率符合負指數模型[10-11]，在海平面的折射率為311，在35 km高空的折射率為1.6。

給定電波射線距離地心最低點的地心距r0和大氣分層厚度hi( i=1～m)后，可計算得出對流層延遲。圖2示意了對流層延遲與最低點海拔高度 h0(其中h0=r0-ae)的關系，最外層大氣的海拔高度取60 km，大氣厚度設為10 m時的計算結果，對應的地心張角如圖3中的曲線Cs所示。

圖3描述對流層延遲取對數后與h0的線性關系，用分段函數擬合，得到如下的公式：

圖3還描述了地心張角Cs（單位弧度）與最低點海拔高度h0（單位m）的線性關系，最小二乘法擬合得到的公式如下：

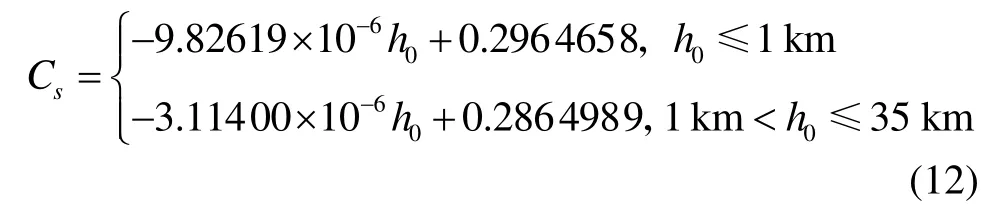
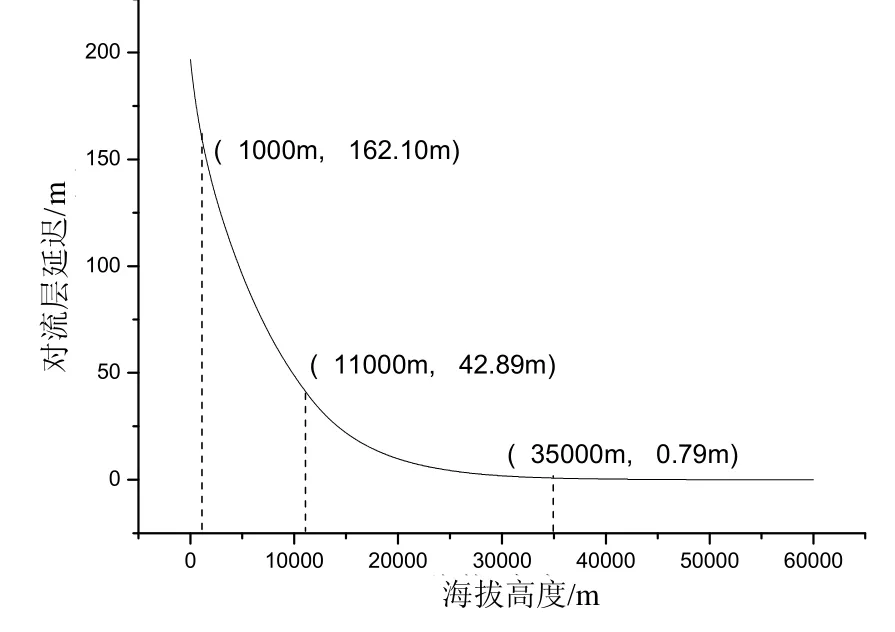
圖 2 對流層延遲隨最低點海拔高度變化曲線Fig.2 Relationship between tropospheric delay and lowest altitude

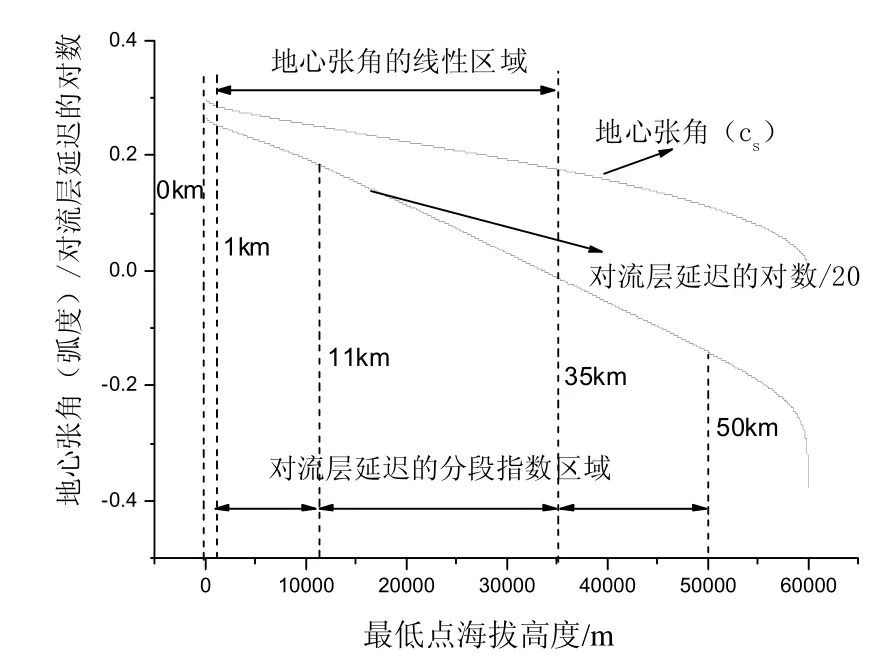
圖3 地心張角及對流層延遲與最低點海拔高度的線性關系Fig.3 Linear relationship between geocentric angle, tropospheric delay and the lowest altitude

3 對流層折射最低點確定方法

當運載火箭飛行高度大于對流層高度時，大氣折射率為1，設運載火箭距離地心的距離為rR，最外層大氣距離地心的距離為點和Am點應用公式(1)，有：

式中，rG為GPS距離地心的距離。根據公式(12)、(14)、(15)，可以計算得出GPS衛星、地心、運載火箭三者之間的夾角：

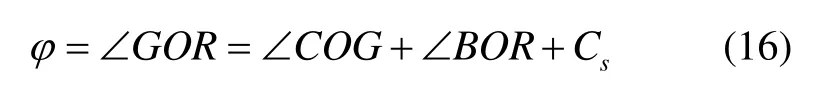
在導航定位計算過程中，容易得到上一次的GPS衛星和運載火箭的位置。在△GOR中，利用余弦定理，有：

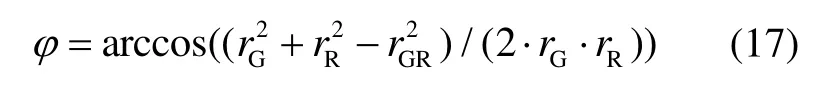
式中，rGR為GPS與運載火箭的直線距離。

根據公式(16)和(17)，利用迭代法可以算出電波射線距離地心最低點的地心距r0，進而根據公式(11)計算得出電離層延遲的大小。

4 對流層延遲計算結果

分析火箭飛行試驗數據，采用內符合精度[12]分析方法得到跟蹤弧段內火箭的位置精度，不考慮對流層延遲改正時得到的結果如圖4所示，圖中兩處波峰分別由2號衛星和5號衛星穿透對流層引起。采用本文提供的對流層延遲改正方法，得到的對流層延遲改正值和最低點海拔高度如圖5所示，其中最低點海拔高度迭代計算的平均次數為10次，定位精度如圖6所示。

圖5表明，對流層延遲改正最大值為135 m，電波折射最低點的海拔高度為6.8 km；圖6表明，采用本文的方法，GPS定位精度從48 m提高到23 m。

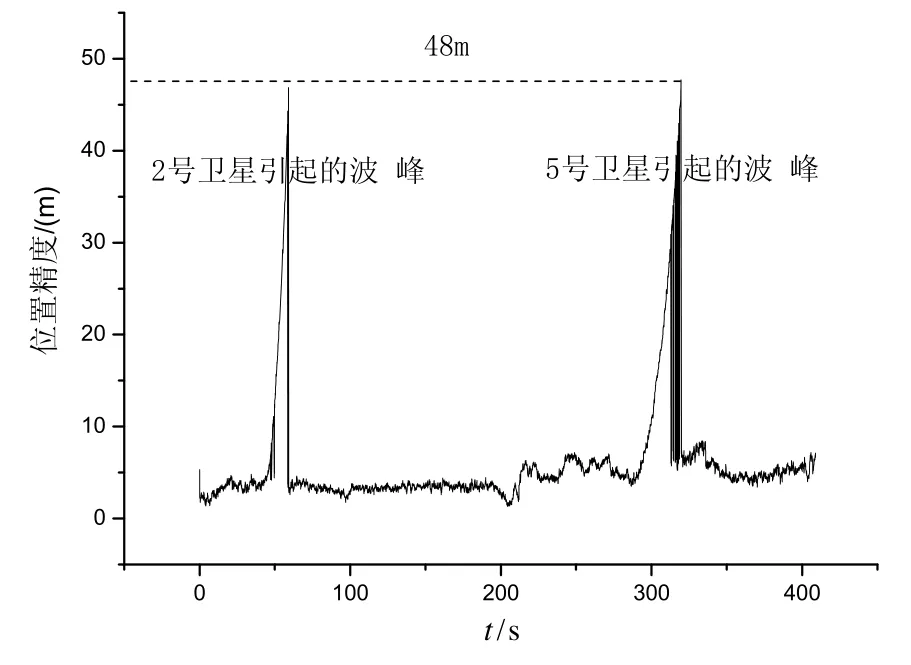
圖 4 箭載GPS位置精度原始曲線圖Fig.4 Original precision of on-board GPS position

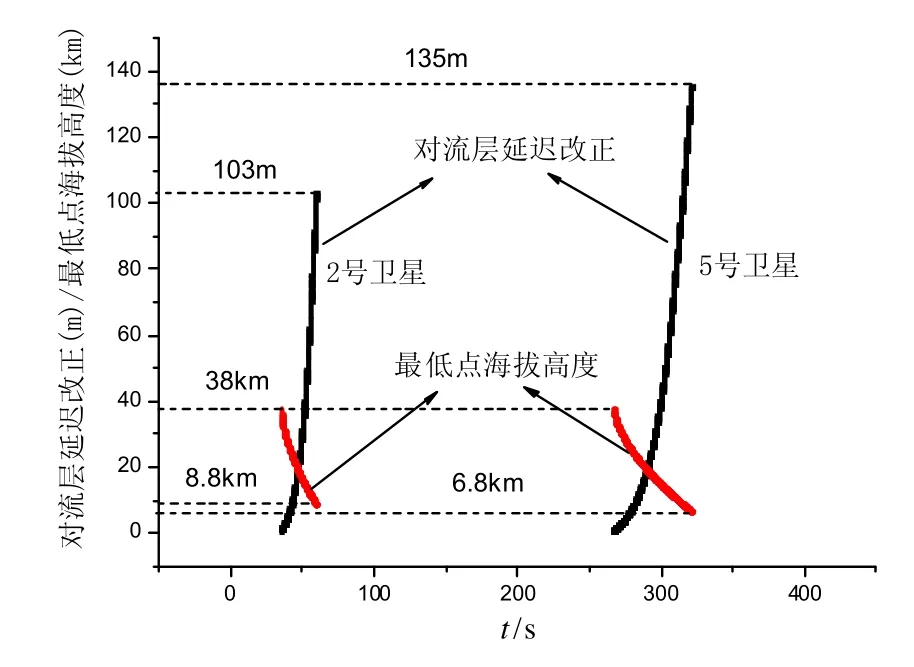
圖 5 對流層延遲改正值及最低點海拔高度關系曲線Fig.5 Relationship between tropospheric delay correction and lowest altitude

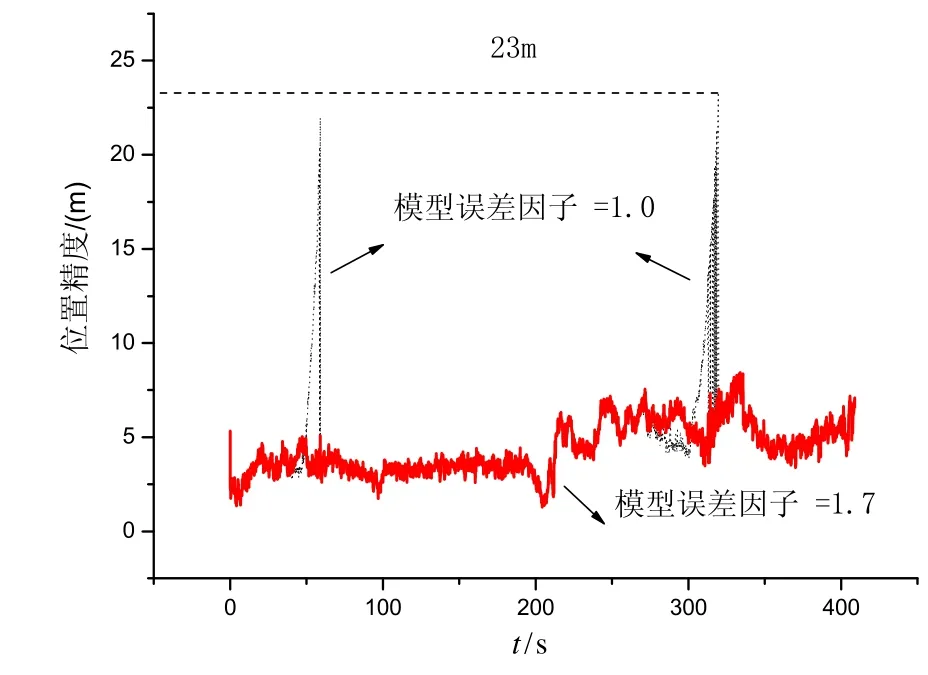
圖 6 箭載GPS定位對流層延遲改正后的位置精度曲線Fig.6 Precision of on-board GPS after tropospheric delay correction

引入模型誤差因子mσ ，對公式(11)的結果進行修正：

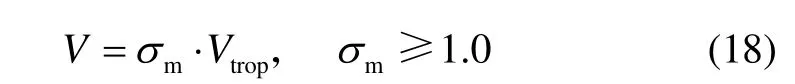
式中，V表示大氣層延遲總誤差，包括對流層延遲和電離層延遲，模型誤差因子包含了電離層延遲誤差、球對稱大氣模型誤差以及大氣折射率計算模型誤差等。圖6顯示了σm分別為1.0和1.7的情況，當σm=1.7時，大氣折射誤差修正被消除，定位精度與屏蔽2號衛星和5號衛星的結果相同。

5 結 論

本文在國際民航組織標準大氣模型的基礎上，采用標準氣象元素計算了大氣折射率，采用射線描跡法對箭載GPS定位時電波穿透對流層進行分析，采用分層求和方法得到了對流層延遲改正與對流層折射最低點海拔高度之間的計算公式，對流層延遲最大可達200 m；通過線性擬合的方法，發現了電波穿透對流層對應的地心張角與最低點海拔高度之間的線性方程，地心張角最大可達17°；提出了根據衛星和火箭之間的夾角與地心張角之間的關系進行迭代計算，進而求得最低點海拔高度的方法。

采用火箭飛行試驗數據對該方法進行了驗證，結果表明，該方法能有效修正對流層延遲，計算方法簡單，適合箭載GPS實時定位。引入了模型誤差因子，以表征誤差改正的實際效果，采用內符合精度作為誤差修正效果的依據。由于未考慮電離層延遲改正，導致模型誤差因子較大，下一步將研究臨近地面的負仰角衛星的電離層延遲改正方法。

（References）：

[1] 趙鐵成, 韓曜旭. GPS定位系統中幾種對流層模型的探討[J]. 全球定位系統, 2011(1): 46-52. Zhao Tie-cheng, Han Yao-xu. Study on several tropospheric models in GPS positioning system[J]. GNSS World of China, 2011(1): 46-52.

[2] 段成林, 馬傳令, 曹建峰, 等. 一種低仰角對流層折射修正的新方法[J]. 紅外與激光工程, 2012, 41(5): 1195-1199. Duan Cheng-lin, Ma Chuan-ling, Cao Jian-feng, et al. A new method on tropospheric refraction correction at low elevation[J]. Infrared and Laser Engineering, 2012, 41(5): 1195-1199.

[3] 潘樹國, 王姍姍, 沈雪峰, 等. 顧及高程差異的網絡差分對流層誤差內插模型[J]. 中國慣性技術學報, 2012, 20(2): 192-195. Pan Shu-guo, Wang Shan-shan, Shen Xue-feng, et al. Interpolation model for troposphere delay error on network differential considering elevation difference[J]. Journal of Chinese Inertial Technology, 2012, 20(2): 192-195.

[4] Rao Ai-shui, Li Yong-gang, Hu Jian, et al. Dynamic calculation method of satellite elevation mask with rocket onboard GPS real-time positioning[C]//China Satellite Navigation Conference 2014 Proceedings. 2014: 27-34.

[5] 李德鑫, 楊日杰, 孫洪星, 等. 基于射線分層算法的電磁波大氣吸收衰減特性分析[J]. 電訊技術, 2012, 52(1): 80-85. Li De-xin, Yang Ri-jie, Sun Hong-xing, et al. Characteristic analysis of atmospheric absorption and attenuation based on rays layering algorithm[J]. Telecommunication Engineering, 2012, 52(1): 80-85.

[6] Wu X L, Hu X G, Wang G, Zhong H J, Tang C P. Evaluation of COMPASS ionospheric model in GNSS positioning[J]. Advances in Space Research, 2012, 51(6): 959-968.

[7] Mcgraw G A. Tropospheric error modeling for high integrity airborne GNSS navigation[J]. Position Location and Navigation Symposium, 2012(4): 158-166.

[8] Rohm W, Bosy J. The verification of GNSS tropospheric tomography model in a mountainous area [J]. Advances in Space Research, 2011, 47(10): 1721- 1730.

[9] Awange J L, Wickert J, Schmidt T, Sharifi MA, Heck B, Fleming K. GNSS remote sensing of the Australian tropopause[J]. Nature Climate Change, 2011, 105: 597-618.

[10] Wang X Y, Wang X L, Dai Z Q, Ke F Y, Cao Y C, Wang F F, Song L C. Tropospheric wet refractivity tomography based on the BeiDou satellite system[J]. Advances in Atmospheric Sciences, 2014.

[11] Bender M, Stosiusa R, Zusa F, et al. GNSS water vapour tomography-expected improvements by combining GPS, GLONASS and Galileo observations[J]. Advances in Space Research, 2011, 47(5): 886-897.

[12] Ren Chao, Peng Jia-di, She Di. Effects of low GPS satellite elevation mask angle on estimation of tropospheric delay[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 125-127.

Tropospheric delay correction model of near ground satellite position using on-board GPS

RAO Ai-shui, LI Qing-mei, HU Jian, WU Guan-peng
(China Satellite Maritime Tracking and Controlling Department, Jiangyin 214431, China)

In view that classical tropospheric delay correction model cannot deal with deviation correction of negative elevation angel satellite, the phenomenon when GPS signal penetrate troposphere using radar ray tracing was modeled based on traditional spherical symmetry standard atmosphere model, and the formulas for computing the correction of tropospheric delay was deduced based on the lowest altitude of troposphere reflection. To calculate the lowest altitude of tropospheric refraction, the liner equation between geocentric angel and the lowest altitude when GPS signal penetrate troposphere was obtained by using least square method. Then a method for calculating the lowest altitude was proposed based on iterative computation using the relationship between the angle of satellite-to-rocket and the geocentric angel. Finally the efficiency of tropospheric delay correction model was evaluated by introducing the model’s error factor. The test data of rocket flight were used to validate the model, and the result proves that the proposed method can eliminate most of the tropospheric delay of up to 135 m, and improve the precision of the near ground satellite position of up to 25 m. This method is especially appropriate to real-time positioning of on-board GPS.

refractive index; refractivity; geocentric angle; ray tracing; atmospheric refraction

V19

：B

2015-05-15；

：2015-08-25

饒愛水（1980—），男，工程師，從事航天測控研究。E-mail：lqmei03@163.com

1005-6734(2015)05-0670-04

10.13695/j.cnki.12-1222/o3.2015.05.019