非線性Klein-Gordon方程的廣義Herm ite譜方法

陶冬亞，焦 琳，王天軍

（1.江蘇師范大學數學與統計學院，江蘇徐州 221116；2.徐州工程學院數學與物理科學學院，江蘇徐州 221111；3.河南科技大學數學與統計學院，河南洛陽 471003）

非線性Klein-Gordon方程的廣義Herm ite譜方法

陶冬亞1，焦 琳2，王天軍3

（1.江蘇師范大學數學與統計學院，江蘇徐州 221116；2.徐州工程學院數學與物理科學學院，江蘇徐州 221111；3.河南科技大學數學與統計學院，河南洛陽 471003）

對于量子力學中的非線性Klein-Gordon方程提出了廣義Hermite譜方法，給出算法格式和收斂性分析，并證明了該方法在空間方向具有譜精度。數值結果表明：所提方法具有有效性，并與理論結果相吻合。

K lein-Gordon方程；廣義Hermite譜方法；譜精度

0 引言

通常的譜方法適應于周期問題或者有界區域上的微分方程［1－4］。文獻［5］考慮了有界區域上一類非線性Klein-Gordon方程的Legendre譜和擬譜方法。但科學工程上的問題往往歸結為無界區域上微分方程，因此，如何求解無界區域上的微分方程是非常重要的。為此，文獻［1－2］將無界區域上的問題轉化成有界區域上的奇異問題，然后利用有界區域上的Jacobi譜方法進行數值求解。然而，變換之后的微分方程的形式變得更加復雜，使得數值分析變得非常困難。一個有效的方法就是使用無界區域上的正交函數直接數值求解原問題［6－11］。最近，文獻［12］提出了一類新的廣義Herm ite正交函數系。這給無界區域問題的數值求解提供了強有力的工具。

非線性Klein-Gordon方程在量子力學中起著重要的作用，求解該方程也成為一些學者關心的熱點［2］。本文將以定義在全直線上的廣義Herm ite正交函數系為基底，提出Klein-Gordon方程新的廣義Herm ite譜方法，并進行數值分析。數值結果表明了新方法的有效性。

1 預備知識

記Hl（x）是次數為l的標準Hermite多項式。對于任意的正實數β，文獻［12］定義了廣義Hermite函數：

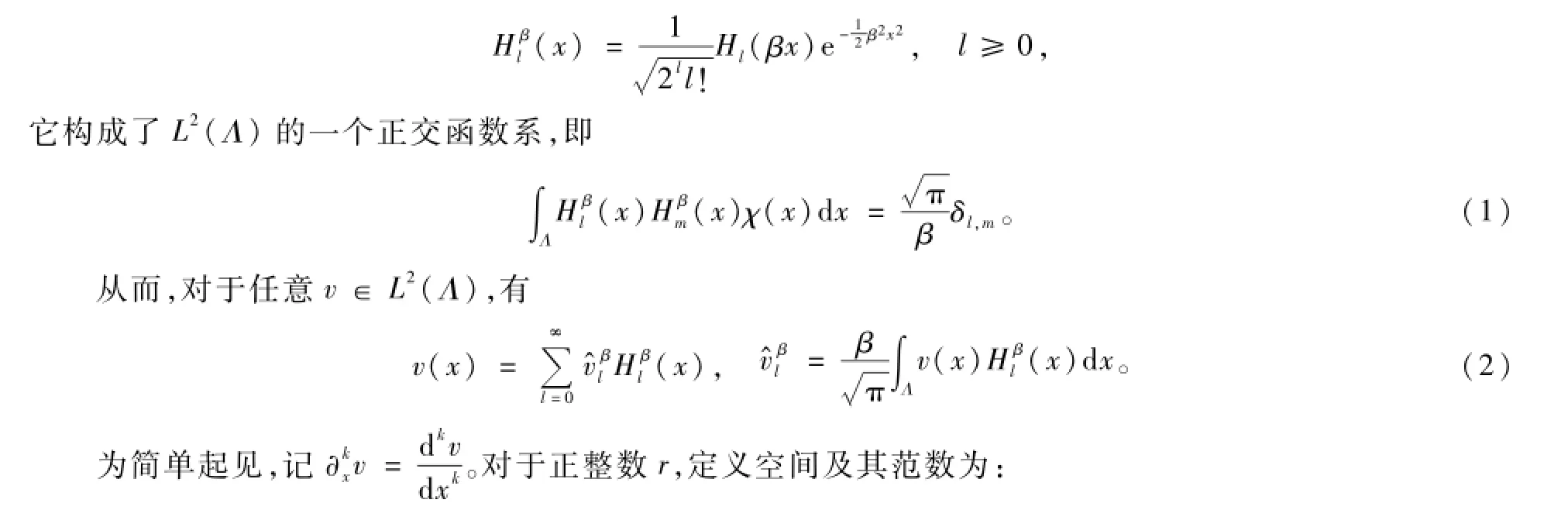
2 Klein-Gordon方程的廣義Herm ite譜方法

2．1 He rm ite譜格式

眾所周知，非線性Klein-Gordon方程在量子力學中起著重要的作用，其一般形式為：

這里假設對于上述所涉及到的范數都是有限的。

3 數值結果

下面將根據譜格式（9）給出數值結果，說明所提格式的有效性。令τ為時間步長。對時間方向用Crank-Nicolson方法進行離散。問題（9）的全離散格式為：

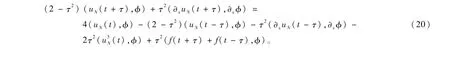
表1 當β＝3時的測試函數（4．3）的逐點誤差

表2分別給出了當τ＝0.001時，逐點誤差與次數N和參數β的依賴關系。顯而易見，隨著N的增大，誤差快速衰減，這與理論分析相吻合，同時也表明通過選取適合的參數β，可以獲得更精確的數值結果。

表2 當τ＝0．001時的測試函數（4．3）的逐點誤差

4 結論

本文對于定義在全直線上的非線性Klein-Gordon方程提出了廣義Hermite譜方法。利用權函數為1的廣義Herm ite函數展開數值解，為數值誤差分析帶來便利。證明該方法在空間上具有譜精度，數值結果也驗證了所提方法的有效性，并與理論分析相吻合。特別是，可適當選取函數e－（βx）2／2中的伸縮因子β，使得數值解更好地逼近正確解。

［1］ Guo B Y，Yi Y G.Generalized Jacobi Rational Spectral Method and Its Applications［J］.J of Sci Comp，2010，43：201－238.

［2］ Wang Z Q，Guo B Y.Legend re Rational Spectral Method for Nonlinear Klein-Gordon Equation［J］.Numer Math A Journal of Chinese Universies：English Seires，2006，15：143－149.

［3］ 王天軍.一類線性奇異邊值問題的譜配置方法［J］.河南科技大學學報：自然科學版，2013，34（6）：75－78.

［4］ 王天軍，賈麗蕊.非線性熱傳導方程的Lagrange插值逼近［J］.河南科技大學學報：自然科學版，2011，31（2）：68－71.

［5］ Guo B Y.Spectral Methods and Their Applications［M］.Singapore：World Scientific，1998.

［6］ Funaro D，Kavian O.Approximation of Some Diffusion Evolution Equations in Unbounded Domains by Hermite Function［J］.Math Comp，1999，57：597－619.

［7］ Guo B Y，Wang T J.Mixed Legendre-Hermite Spectral Method for Heat Transfer in an Infinite Plate［J］.Comp and Math with Appl，2006，51：751－768.

［8］ Guo B Y，Shen J，Xu C L.Spectral and Pseudospectral Approximations Using Herm ite Functions：Application to the Dirac Equation［J］.Adv in Comp Math，2003，19（1／3）：35－55.

［9］ Fok JC M，Guo B Y，Tang T.Combined Hermite Spectral-finite Difference Method for the Fokker-Planck Equation［J］. Math Comp，2002，71（240）：1497－1528.

［10］ Ma H P，Sun W W，Tang T.Hermite Spectral Methods with a Time Dependent Scaling for Parabolic Equations in Unbounded Domains［J］.SIAM JNumer Anal，2005，43：58－75.

［11］ Ma H P，Zhao T G.A Stabilized Hermite Spectral Method for Second-order Differential Equations in Unbounded Domain［J］.Numer Meth for PDEs，2007，23：968－983.

［12］ Xiang X M，Wang Z Q.Generalized Hermite Spectral Method and Its Applications to Problems in Unbounded Domains［J］.SIAM JNumer Anal，2010，48：231－1253.

O175.2

A

1672－6871（2015）05－0087－05

國家自然科學基金項目（11371123，11171227）；河南省教育廳自然科學基金項目（14B11021）；河南科技大學博士啟動基金項目（09001263）

陶冬亞（1977－），女，江蘇徐州人，講師，碩士，研究方向為偏微分方程數值解；王天軍（1963－），男，通信作者，河南息縣人，副教授，博士，碩士生導師，研究方向為偏微分方程數值解.

2015－04－30