（λ，μ）模糊軟環與（λ，μ）模糊軟理想

周 鋒，姚炳學

（聊城大學數學科學學院，山東聊城 252059）

（λ，μ）模糊軟環與（λ，μ）模糊軟理想

周 鋒，姚炳學

（聊城大學數學科學學院，山東聊城 252059）

針對軟集代數結構問題，利用（λ，μ）模糊代數理論，在模糊軟集理論的基礎上，引入了（λ，μ）模糊軟環的概念，討論了它們的相關性質。同時，將同態與同構應用到（λ，μ）模糊軟環中，并建立了模糊軟同態下（λ，μ）模糊軟環與（λ，μ）模糊軟理想對應的定理。

軟環；模糊軟環；（λ，μ）模糊軟環；（λ，μ）模糊軟理想

0 引言

在實際生活中，很多問題并不能利用傳統的數學方法解決。1965年，文獻［1］提出的模糊集理論成為一種解決模糊類型問題的有力的數學工具。之后，許多學者對模糊集的相關理論進行了研究［2－6］。為了更好地解決不確定問題，文獻［7］引入了軟集的概念。文獻［8］引入了模糊軟集的概念。文獻［9］進一步研究了模糊軟群的性質。文獻［10］探究了模糊軟環與模糊軟理想。從此，模糊集應用到了軟集理論上，得出很多模糊軟集的相關結論。

本文利用模糊集理論將模糊軟環進行推廣，給出了模糊軟環的概念，指出了（λ，μ）模糊軟環是模糊軟環的推廣，并討論了其關于軟集的交、并運算的性質，探究了（λ，μ）模糊軟環在環的軟同態映射下的像以及原像的性質。本文為進一步刻畫（λ，μ）模糊軟理想代數結構特征奠定了基礎。

1 預備知識

在本文中R表示一個環，λ、μ為常數，0≤λ＜μ≤1。

定義1［5］設U為初始論域，E為參數集，P（U）為U的冪集，A?E，稱（F，A）為U的軟集。這里，F為映射，F：A→P（U）。

定義2［11］設U為初始論域，E為參數集，F（U）為U的所有模糊子集的全體，A?E，稱（F，A）為U的模糊軟集。這里，F為映射，F：A→F（U）。

定義3［11］設（F，A）和（H，B）為論域U的模糊軟集，若：（1）A?B；（2）?a∈A，F（a）?H（a），則稱（F，A）和（H，B）的模糊軟子集，記為（F，A）?（H，B）。若：（F，A）?（H，B）且（H，B）?（F，A），則稱（F，A）和（H，B）模糊軟相等，記為（F，A）＝（H，B）。

定義4［12］設（F，A）和（H，B）為論域U的模糊軟集，記（F，A）和（H，B）的交為（F，A）∩（H，B）＝（K，C），其中，C＝A∩B，?c∈C，K（c）＝F（c）∩H（c）。

定義5［12］設（F，A）和（H，B）為論域U的模糊軟集，記（F，A）和（H，B）的并為（F，A）∪

定義6［13］設（F，A）為論域U的模糊軟集，?t∈［0，1］，稱軟集（F，A）t＝（Ft，A）為（F，A）的t-水平截集，其中，

2 （λ，μ）模糊軟環

定義7［10］設（F，A）為R的一個軟集，若?a∈A，F（a）是R的一個子環，則稱（F，A）為R的一個軟環。

定義8設（F，A）為R的模糊軟集，若?a∈A，F（a）是R的（λ，μ）模糊子環，則稱（F，A）為R的（λ，μ）模糊軟環。

定義9［14］設A為R的模糊子集，則A為R的（λ，μ）模糊子環的充分必要條件是：?x，y∈R，（1）A（x－y）∨λ≥（A（x）∧A（y））∧μ；（2）A（xy）∨λ≥（A（x）∧A（y））∧μ。

定理1設（F，A）為R的模糊軟集，則（F，A）為R的（λ，μ）模糊軟環的充分必要條件是：?a∈A，?x，y∈R，（1）F（a）（x－y）∨λ≥（F（a）（x）∧F（a）（y））∧μ；（2）F（a）（xy）∨λ≥（F（a）（x）∧F（a）（y））∧μ。

定理2設（F，A）為R的（λ，μ）模糊軟環，則?x∈R，?a∈A，F（a）（0）∨λ≥F（a）（x）∧μ。特別地，如果?x0∈R，?a0∈A，使得F（a0）（x0）≥μ，則F（a0）（0）≥μ。

定理3設（F，A）為R的模糊軟集，則（F，A）為R的（λ，μ）模糊軟環的充分必要條件是：?t∈（λ，μ］，則（F，A）t為R的軟環。

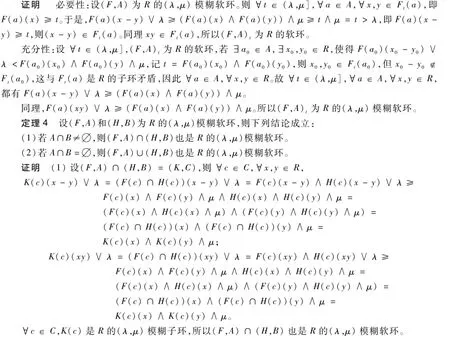
（2）設（F，A）∪（H，B）＝（K，C），由于A∩B＝?，則?c∈C，K（c）＝F（c）或者K（c）＝H（c）。由于F（c），H（c）都是R的（λ，μ）模糊軟環，故?c∈C，K（c）是R的（λ，μ）模糊軟環，所以（F，A）∪（H，B）也是R的（λ，μ）模糊軟環。

定理5設（F，A）和（H，B）為R的（λ，μ）模糊軟環，若（H，B）是（F，A）模糊軟子環。則稱（H，B）是（F，A）的（λ，μ）模糊軟子環，記為（H，B）?（F，A）。

引理1［14］設f：R1→R2為環的同態映射，若γ為R1的（λ，μ）模糊子環，則f（γ）為R2的（λ，μ）模糊子環。

定義10［10］設（F，A），（H，B）分別為R1，R2的模糊軟環，映射f：R1→R2，g：A→B。若滿足：（1）f為R1到R2的環同態映射；（2）g為A到B的滿射；（3）?a∈A，f（F（a））＝H（g（a）），則稱（f，g）為模糊軟同態映射。當f為滿射時，則稱（F，A）與（H，B）關于（f，g）模糊軟同態。

定理6設（F，A），（H，B）分別為R1，R2的模糊軟環，（F，A）與（H，B）關于（f，g）模糊軟同態。若（F，A）為R1的（λ，μ）模糊軟子環，則（H，B）為R2的（λ，μ）模糊軟子環。

證明由于（F，A）與（H，B）關于（f，g）模糊軟同態，即?a∈A，f（F（a））＝H（g（a））。由于g為A到B的滿射，則?β∈B，?α∈A，使得g（a）＝β，所以H（β）＝H（g（α））＝f（F（α））。由引理1知：f（F（α））為R2的（λ，μ）模糊軟子環，即H（β）為R2的（λ，μ）模糊軟子環。由定義8知：則（H，B）為R2的（λ，μ）模糊軟子環。

3 （λ，μ）模糊軟理想

定義11設（F，A）為R的模糊軟集，若?a∈A，F（a）是R的（λ，μ）模糊理想，則稱（F，A）為R的（λ，μ）模糊軟理想。

［1］ Zadeh L A.Fuzzy Sets［J］.Inform and Control，1965，8（1）：338－353.

［2］ Rosenfeld A.Fuzzy Groups［J］.Math Anal Appl，1971，35：512－517.

［3］ Bhakat S K，Das P.（∈，∈∨q）Fuzzy Subgroups［J］.Fuzzy Sets and System s，1996，80：359－368.

［4］ Yao B.（λ，μ）Fuzzy Normal Subgroups and（λ，μ）Fuzzy Quotient Subgroups［J］.The Journal of Fuzzy Mathematics，2005，13（3）：695－705.

［5］ 孫小慧，吳濤，孫恒，等.一種基于區間直覺模糊集的多屬性決策方法［J］.河南科技大學學報：自然科學版，2013，34（5）：87－90.

［6］ 劉鑫琳，黎昌珍.直覺梯形模糊數集成算子及在群決策中的應用［J］.河南科技大學學報：自然科學版，2014，35（6）：88－93.

［7］ Molodtsov D.Soft Set Theory-first Results［J］.Computer and Mathematics Application，1999，37（4／5）：19－31.

［8］ Maji P k，Roy A R，Biswas R.Soft Set Theory［J］.Computer and Mathematics Application，2003，45（4／5）：555－562.

［9］ 閻瑞霞，劉金良，姚炳學.模糊軟集與模糊軟群［J］.數學的實踐與認識，2010，40（8）：144－148.

［10］ Ebubekir I，Mehmet A O.Fuzzy Soft Rings and Fuzzy Soft Ideals［J］.Neural Computing and Applications，2012，21（1）：1－8.

［11］ Maji P K，Biswas R，Roy A R.Fuzzy Soft Sets［J］.The Journal of Fuzzy Mathematics，2001，9（3）：589－602.

［12］ Ali M I，Feng F，Liu X.et al.On Some New Operations in Soft Set Theory［J］.Computer and Mathematics Application，2009，57：1547－1553.

［13］ Aygunohlu A，Aygun H.Introduction to Fuzzy Soft Groups［J］.Computer and Mathematics Application，2009，58（6）：1279－1286.

［14］ 姚炳學.群與環上的模糊理論［M］.北京：科學出版社，2008.

O153

A

1672－6871（2015）05－0097－03

國家自然科學基金項目（11471152）

周 鋒（1987－），男，山東滕州人，碩士生；姚炳學（1963－），男，山東諸城人，教授，博士，碩士生導師，研究方向為模糊系統與粗糙集理論.

2014－11－12

基金項目：國家水體污染控制與治理科技重大專項基金項目（2012ZX07204－001－02－01）

作者簡介：王振國（1990－），男，河南濮陽人，碩士生；何爭光（1963－），男，河南孟州人，教授，博士，博士生導師，主要研究方向為水污染處理技術.

收稿日期：2015－04－02