基于HMM-PNN模型的助推段目標類型識別

王 普，樊建鵬，程洪瑋，司馬端

（1.國防科技大學電子科學與工程學院，湖南長沙410073；2.北京跟蹤與通信技術研究所，北京100094）

基于HMM-PNN模型的助推段目標類型識別

王 普1，樊建鵬1，程洪瑋2，司馬端1

（1.國防科技大學電子科學與工程學院，湖南長沙410073；2.北京跟蹤與通信技術研究所，北京100094）

針對衛星視野下導彈目標的識別問題，將經典隱馬爾科夫模型（HMM）識別算法應用在助推段目標類型識別上并加以改進。首先，分析了通用彈道助推段運動特性，確定了不同射程導彈的分類依據。其次，針對HMM模型時序特性差異較小而引起的識別率低的問題，引入概率神經網絡（PNN）與HMM模型相結合的結構算法，該方法整合了HMM模型的時間序列數據處理能力和PNN的自學習能力、貝葉斯決策理論，對不同射程導彈目標實現了分類識別。仿真實驗結果表明該算法是一種有效的導彈目標識別算法，識別率優于傳統的HMM模型方法，誤判率較低，且易于工程實現。

HMM-PNN模型；助推段彈道模型；時序特征；目標識別

0 引言

導彈防御中，在敵方導彈發射后數十秒實現導彈類型初步識別是十分重要的。但目前的導彈目標識別大多是基于雷達平臺，當來襲導彈目標處于助推段時，常規的預警雷達由于自身盲區限制探測不到目標，而星載探測器則可以探測到目標，并通過多星關聯和連續觀測實現對目標的定位和跟蹤，從而得到助推段彈道和輻射數據。如果能從中進行目標識別，則可以提高識別的實效性。但是受探測器條件限制，目前利用尾焰輻射信息只能粗略識別小射程戰術導彈和遠程洲際戰略導彈，對于射程較小的彈道導彈識別效果不好，識別率低。本文重點研究單從運動特性上識別不同類型導彈的可能性問題。

文獻［1］提出了基于導彈預警衛星系統的目標識別算法，利用導彈發射點位置、導彈尾焰紅外特征和關機點特征三個狀態量特征進行不同類型導彈的識別。該算法中關機點參數的判別權值最大，對其準確度要求很高。文獻［2］通過隱馬爾科夫模型（HMM）來分別不同類型的彈道導彈，該算法主要利用中段彈道數據差異性進行分類，無法實現助推段早期快速識別。本文對三種不同類型的導彈彈道助推段數據進行分析，發現其運動特性差異，特別是后助推段速度大小等特征量差異明顯，這使得在助推段對來襲導彈目標進行初判決成為可能。并在前文研究的基礎上，改進了HMM對差異不明顯的模式辨識能力差的缺點，引入概率神經網絡（PNN）和HMM進行結合，利用PNN進行后驗概率的估計，對HMM誤判的識別結果進行修正，將改進算法應用在助推段導彈目標類型識別中。

1 助推段運動模型分析

助推段是指導彈從發射到發動機關機所持續的過程。助推段導彈受力復雜，很難用模型準確地描述。導彈發射后向上作垂直運動，隨后在制導系統控制下依照程序緩慢轉向目標方向，得到預定的最佳拋射角，最后瞄準直到發動機關機。此時，導彈射向基本保持不變，通過控制不同的關機時間來控制射程以及落點［3］。

不同類型導彈的助推段彈道運動特性的差異主要在于發動機推力作用的不同，彈道導彈發動機推力可表示為：

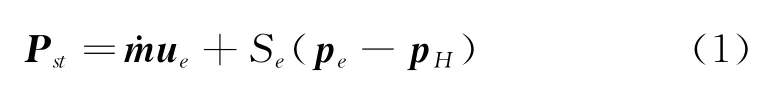
式中，Pst為發動機推力，Se為排氣速度，pe、pH分別為排氣端面氣壓和外部大氣壓。由（1）式可知，發動機推力的大小由燃料燃燒噴出氣體的速度和排氣端面的氣壓差決定，額定射程的導彈受上述因素的影響而使得各自的推力不同。對助推段導彈進行受力分析，由牛頓第二定律可得出導彈的動力學方程如下：

ma=Pst+mg+R+Fc+F＇k+F＇rel（2）式中，pst為發動機推力靜分量矢量，R為導彈氣動力矢量，Fc為導彈控制力分量矢量，F＇k、F＇rel分別為附加哥氏力和附加相對力。

設ECF坐標系下狀態變量為：

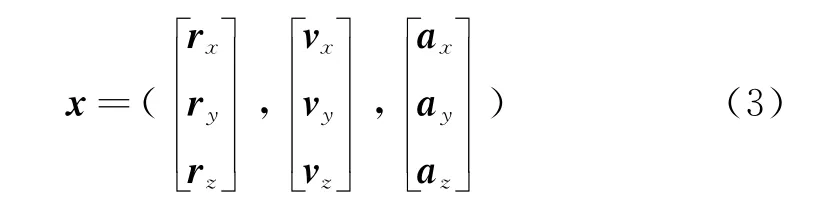
式中，r，v，a分別是目標位置矢量、速度矢量和加速度矢量。典型的彈道導彈基本保持零攻角，推力與相對速度矢量平行，因此遵循重力轉彎彈道，則目標運動方程為：

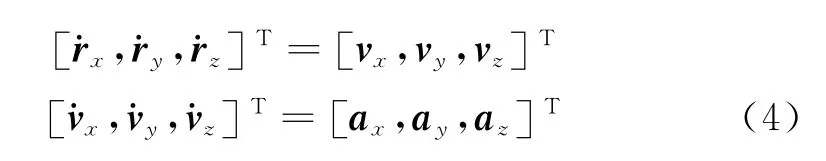
在助推段，導彈主要在大氣層內飛行，導彈受到推力、大氣阻力和地球引力的作用，根據導彈發動機燃料及構造的不同，推力也有很大變化。從上述分析可知，對于不同射程彈道導彈，其推力的大小與持續時間的差異性會導致目標在位置、速度和加速度大小上的不同，受探測及跟蹤精度的限制，單個點的差異可能會有較大的誤差并顯示出一定的隨機性，因此試驗中選擇助推段一段時序數據，其差異性較單個點明顯，理論上可以提取出用以區分上述不同目標的時序特征向量。

2 HMM-PNN模型與算法

HMM-PNN模型是HMM模型與PNN模型整合改進的結果。導彈彈道運動參數可以看作若干個參數表示的N維時序集合Q=｛q1，q2，……，qn｝，由于HMM模型具備時序建模與推理能力，可用于對彈道的時序分量進行建模。PNN融合了密度函數估計、貝葉斯決策理論以及神經網絡強大的自學習能力，但是不具備時序建模能力。此外，對于助推段，導彈目標的彈道差異性并不會像中段那樣明顯，HMM概率計算的隨機性與訓練樣本數目不足會使計算概率與實際結果不相符，導致識別率不高，誤判明顯。而PNN可以最大程度地利用誤判先驗知識，按貝葉斯最小風險準則將輸入向量分到具有最大后驗概率值的類別中去，因此將兩者結合起來可以提高識別效果［4］。

通過以上的分析，本文將HMM模型的時序建模能力與PNN相整合，對彈道建立模型，其結構圖如圖1所示。

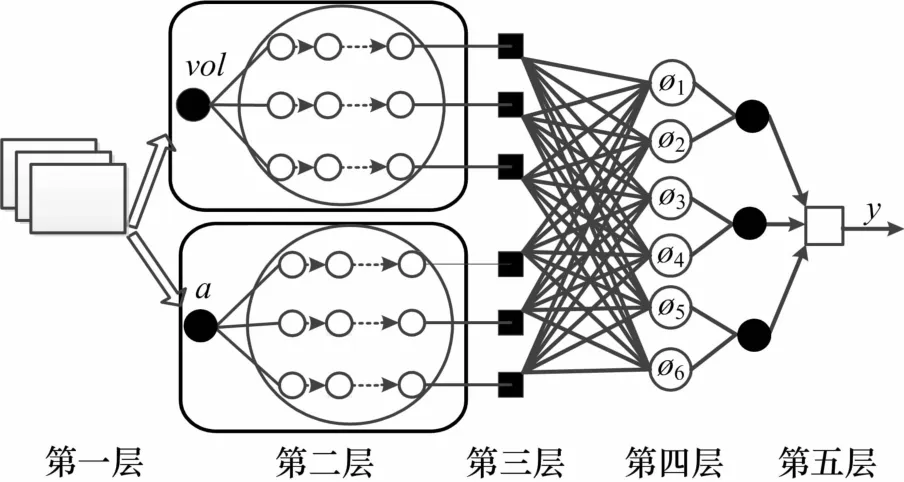
圖1 HMM-PNN模型結構圖

如圖1所示，HMM-PNN模型包括五層結構，分為兩大環節，其中第一層和第二層為HMM時序建模環節，第三、四、五層為概率神經網絡模型環節。

時序建模環節主要體現的是利用彈道時序特征對不同類彈道建模的過程。本實驗中，初步設定有三類不同射程導彈，即對于每一種輸入特征向量，都有三條不同的馬爾科夫鏈對應三種不同的彈道，特定類別的HMM模型關于該類別彈道數據具備的似然概率最大，由此得到如圖2所示HMM層的隱馬爾科夫結構模型，其中上半部分為速度特征向量對應的模型vol-HMM，下半部分為加速度模型a-HMM，其他模型定義以此對應。目前關于HMM類型選擇沒有統一的規則方法，但根據導彈的運動特點，本算法采用的結構是left-right形式的Bakis模型，Bakis模型的拓撲結構簡單、參數較少、訓練過程簡單快速、較容易收斂，是目前研究較多且較成熟的類型［5］。

圖2 HMM模型示意圖

模型建立后需要對模型進行訓練與可靠性驗證，通常為了使不同樣本都適用于該模型，需要對輸入時序序列進行量化處理，本文用到的k均值量化算法的基礎是最小誤差平方和準則，其代價函數為：

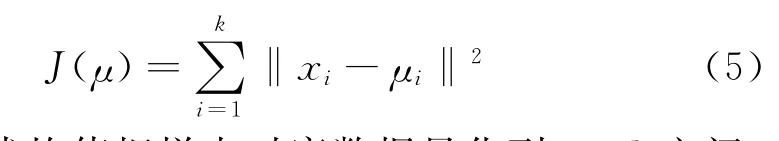
利用迭代均值把樣本時序數據量化到0～k之間，為了為加快算法的訓練速度，本實驗中k值與觀測數一致。k值的選擇根據時序數據維數大小決定，太小影響識別精度，太大則會導致概率計算迭代不收斂。

HMM模型的訓練即在已知訓練樣本觀測序列O =（o1，o2，…，oT）的情況下，估計模型λ=（π，A，B）參數：隱狀態序列的轉移概率｛aij｝和可見狀態序列的產生概率｛bjk｝，使得在該模型下觀測概率p（O/λ）最大。Baum-Welch算法是基于最大似然估計的思想，可見序列v條件下從隱狀態ui（t-1）轉移到ui（t）的概率γij（t）為：

式中，αi（t）、βj（t）分別為在t時刻位于隱狀態ui且已產生了到t時刻位置的可見序列概率和已產生了t時刻之后的可見序列概率。公式（7）給出了隱狀態ui到uj的轉移概率估計?aij，隱狀態uj產生顯狀態vk的概率估計?bjk，通過遞歸方式更新參數估計，從而得到更利于樣本序列出現的模型參數。

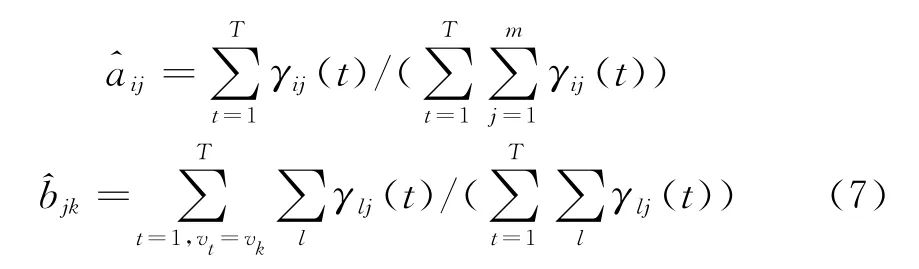
訓練完成后，通過計算訓練樣本在模型λ=（π，A，B）下出現的概率p（ O|λ）來判斷模型的可靠性。前向算法根據訓練的模型參數，利用遞推公式（8），計算到t+1時刻部分觀測序列為o1，o2，…，ot，ot+1且在時刻t+1處于qi的前向概率，再利用公式（9）計算出p（O/λ）。

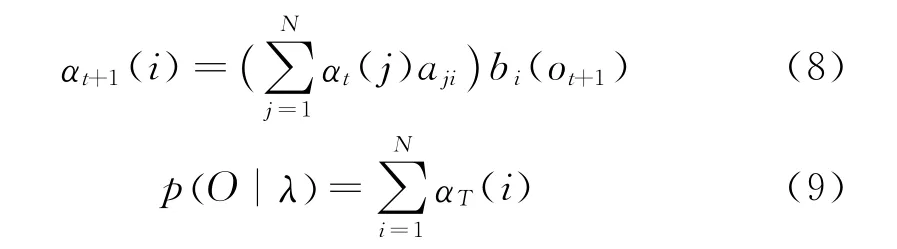
式中，i=1，2，…，N。根據對應馬爾科夫鏈輸出前向概率的大小來判斷類別［6］。

以上介紹了時序建模的過程以及利用經典HMM完成識別的算法。然而，該算法是針對單個特征向量的識別，對助推段小差異性特征識別率不高，因此本文算法在此基礎上，對多個時序特征HMM模型的輸出進行特征融合，將其輸入PNN模型。

神經網絡識別環節中，第三層為隱含層的徑向基層，徑向基層中每一個神經元節點擁有一個中心，該層接收輸入層的樣本輸入，計算輸入向量與中心的距離，最后返回一個標量值，該層中所確定的輸入/輸出關系式定義如下：

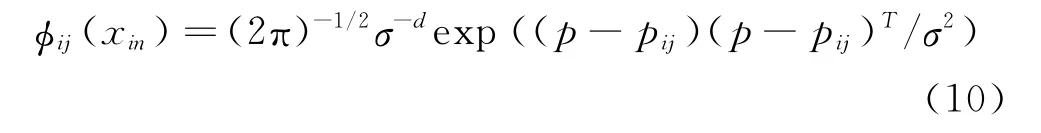
求和層各單元只與相應類別的模式單元相連，并把隱含層屬于同一類的隱含神經元的輸出做加權平均：

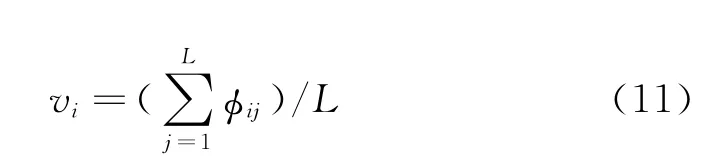
式中，i為訓練樣本的總類數，φij是第i類樣本的第j個中心，L表示第i類的神經元個數。最后估計各類的概率，求和層神經元個數與類別數一致。輸出層取求和層中最大的一個作為輸出的類別：

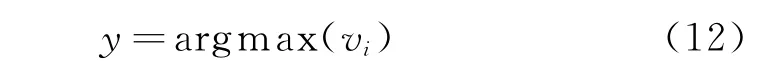
利用樣本數據對神經網絡的各神經元權值和閾值進行訓練，最后利用測試數據驗證網絡。HMM-PNN算法詳細步驟為：

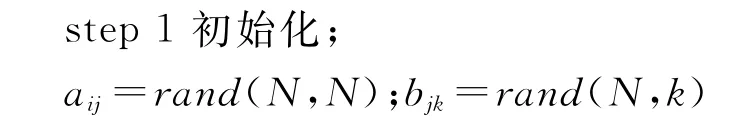
step 2量化后序列用aij（l-1）和bjk（l-1）估計?aij（l）和?bjk（l）；

step 3對于估計值aij（l）和bjk（l），若aij（l）-aij（l-1）、bjk（l）-bjk（l-1）小于閾值θ，轉到step 4，否則轉到step 2；

step 4返回aij和bjk，計算前向概率；

step 5融合不同特征模型的輸出概率作為PNN輸入，對PNN進行訓練、測試；

step 6結束，輸出識別結果y。

3 仿真實驗

由于缺乏導彈實測樣本數據，本實驗數據來源于導彈六自由度彈道模型的仿真。實驗驗證上文中關于助推段彈道的理論，確定分類的依據。通過識別率、識別時間等試驗結果驗證本文算法。

3.1 助推段特性驗證分析

衛星首次探測到目標發射，加上跟蹤、濾波預處理等，接收到估計數據為數十秒左右，而彈道導彈的關機點大概為120～200s左右，助推段時間較短，給特征提取帶來了困難，通過對助推段彈道估計數據進行分析，證明助推段不同射程導彈的可區分性。

實驗選取800～1200km、2300～2700km、3500～4000km射程的三類導彈共900個彈道數據，每組數據采樣率為1 Hz，濾波輸出的數據各加上一定大小的隨機噪聲誤差。首先驗證部分數據的真實性，圖3表示通用彈道射程r、高度h、速度v、加速度a的一般特性，并比較了整個彈道的三種特征的特性差異，可以看出從整個彈道來說，助推段差異不明顯，顯示出的是中段明顯的差異。但是單從助推段來說，三類不同射程的導彈運動特性也存在差異性。

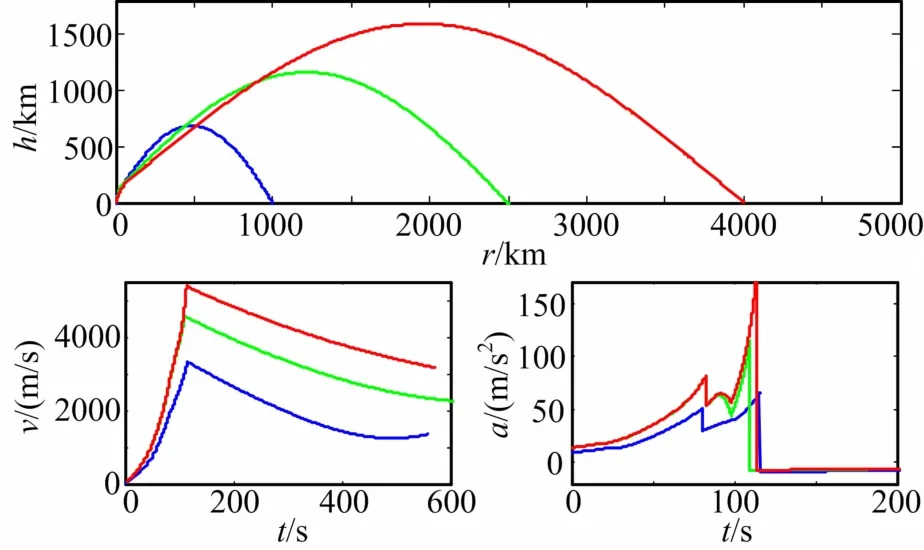
圖3 彈道特性對比圖

圖4 中分別表示目標在助推段的位置、速度和加速度大小特性曲線，由此可以發現對于不同射程的彈道導彈，在助推段里，距地心的距離h、速度v、加速度a大小有差異性，與前文理論設想相似，但距離曲線在整個助推段沒有一致差異性，究其原因在于沒有考慮到影響地心距離的拋射角、彈道傾角等因素的作用。

速度、加速度大小曲線顯示這三類不同射程運動特性中有一致的可區分差異性，符合前文理論分析。此外低射程彈道與其他兩種射程導彈的差異性明顯，而后兩種射程導彈差異性較小，分析認為可能與不同射程的建模不一樣有關。

3.2 算法仿真

在仿真計算機CPU為Core2 Duo E7400、2.79GHZ，內存為4GB的情況下，使用Matlab工具進行仿真計算。

仿真實驗中，數據選取為助推段41～100s數據。π設為［1，0，0，0，0，0，0，0］，A和B采用隨機數獲得。神經網絡調用神經網絡工具箱默認的概率神經網絡，spread值設為1.5。本實驗首先對原算法進行驗證，各用200個樣本數據，首先用各類100個數據訓練對應HMM模型參數，訓練完成后利用剩余的各100組數據進行測試，仿真如圖5所示。真實值和期望值曲線重合度越高代表識別效果越好，則可以看出對第一類樣本的識別率較高，第二、三類樣本的識別率偏低，且第二、三類容易相互誤識別。究其原因在于，第一類與第二、三類特性差異性明顯，而第二、三類雖有差異但是較小，加上HMM的局限性，導致識別率較低。

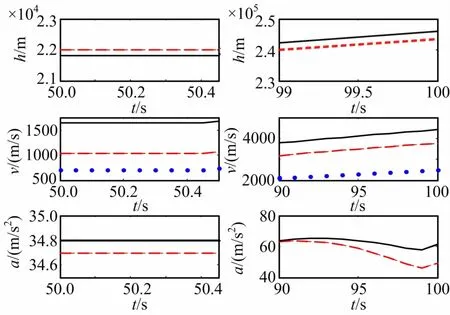
圖4 助推段特性差異對比圖

圖5 HMM模型識別結果

接下來驗證HMM-PNN模型，由于HMM-PNN模型需要HMM參數的訓練和概率神經網絡訓練，為了保證兩次實驗的一致性，選取三種彈道各200個彈道時序數據，同樣選取各類任意100個數據訓練HMM模型參數，訓練完成后，選取剩余的各類任意100個數據輸入到訓練好的HMM模型計算前向概率p（O/λ），將輸出的100組輸出概率融合數據用來訓練概率神經網絡，完成HMM-PNN模型的訓練過程。將剩余各類100個數據作為測試數據，輸入到訓練好的HMM-PNN模型，識別結果如圖6所示。

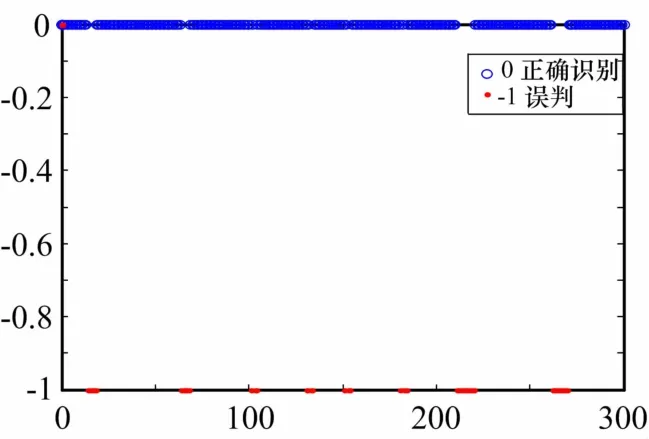
圖6 HMM-PNN輸出識別效果圖

圖6 顯示HMM-PNN模型的識別效果，“-1”代表誤判，識別率明顯比HMM模型高，可見算法的有效性。表1給出了分模塊速度HMM模型vol-HMM和加速度HMM模型a-HMM的識別率，以及HMM模型平均識別率與本文算法識別率的對比情況。

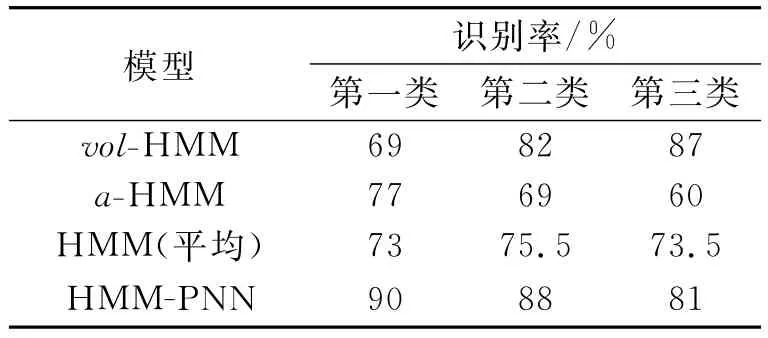
表l 本文方法與傳統HMM識別率對比

仿真實驗結果表明，本文算法識別率較傳統HMM算法有較大提高，使得彈道識別有較高的準確性。誠然，兩層結構模型犧牲了一定的實時性，但在離線樣本數據庫訓練完成的情況下，本文算法中PNN單層網絡在線識別過程耗時0.0527s，整個算法樣本在線識別過程耗時0.1577s，因此HMM-PNN模型識別算法滿足對助推段不同射程彈道識別的準確性與實時性要求。

4 結束語

本文初步分析了導彈助推段模型運動特性并用仿真試驗進行了驗證，以不同射程導彈兩個運動時序特性的差異性為依據，將HMM-PNN模型算法運用在助推段不同類型導彈的識別上，對來襲目標進行了初判別。并依托導彈運動模型，進行了相關的仿真實驗，仿真結果表明該算法能夠有效識別出不同范圍射程的導彈目標，與傳統中段彈道導彈識別相比識別率較高，能較早地識別出來襲目標。但是，本實驗中助推段提取時序特征較少，對彈道的描述不夠完整，還有待進一步研究。■

［1］ 趙延，姚康澤，等.導彈預警衛星目標識別算法研究［J］.系統工程與電子技術，2005，27（10）：1811-1813.

［2］ Singh Uk，padmanabhan V.Training and classification of ballistic missiles using Hidden Markov Model［C］∥Contemporary Computing（IC3），IEEE 2013 Sixth International Conference，2013：301-306.

［3］ 曹賀.基于天基預警系統的導彈助推段彈道估計算法研究［D］.哈爾濱：哈爾濱工業大學，2006.

［4］ 飛思科技產品研發中心.神經網絡理論與matlab7實現［M］.北京：電子工業出版社，2005.

［5］ 王西穎，戴國忠，等.基于HMM-FNN模型的復雜動態手勢識別［J］.軟件學報，2008，19（9）.

［6］ 李航.統計學習方法［M］.北京：清華大學出版社，2012.

Trajectory classification based on HMM-PNN model in boost phase

Wang Pu1，Fan Jianpeng1，Cheng Hongwei2，Sima Duan1
（1.College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，Hunan，China；2.Beijing Institute of Tracking and Telecommunication Technology，Beijing 100094，China）

An algorithm of trajectory classification based on classical Hidden Markov Model for early warning satellite system is established and improved in boost phase.First，the classification basis established by analyzing the time sequence property of the normal boost trajectory.Then，an structure algorithm combined HMM model with PNN model is introduced to solve the question of low rate of recognition caused by the less obvious difference among the trajectory，which integrated the capacity of time sequence processing for HMM and the Bayesian decision theory for PNN.Feasibility and effectiveness of the algorithm is verified by simulation experiments.Analysis of the result shows that its performance is remarkably improved compared to traditional HMM method，with its implementation suitable for engineering fulfillment.

H MM-PNN model；trajectory model；time sequence property；target recognition

TN971；V474.2+7

A

2015-03-20；2015-07-01修回。

王普（1991-），男，碩士研究生，研究方向為空間信息獲取與處理。