一種基于優化算法的多波束賦形方法

楊佳敏

（中國航天科工集團8511研究所，江蘇南京210007）

一種基于優化算法的多波束賦形方法

楊佳敏

（中國航天科工集團8511研究所，江蘇南京210007）

針對穩健的自適應波束形成，研究多波束賦形方法，闡述了波束域的賦形方法，并研究分析了波束賦形算法，驗證了多波束賦形方法能夠增強波束的穩健性。提出的多波束賦形算法實現簡單，賦形效果良好，再經過智能算法對多個波束的幅度相位進行優化后，能夠獲得主瓣平坦的波束方向圖。仿真結果驗證了其能夠獲得理想的波束方向圖，不僅能夠展寬主瓣寬度，而且使主瓣增益增大，從而增強了波束的穩健性。

自適應波束形成；穩健性；多波束賦形

0 引言

無線通信系統常常要求天線陣列形成具有特定的主瓣寬度與形狀的方向圖，也就是需要進行波束賦形。波束賦形也就是陣列天線的方向圖綜合。方向圖綜合是通過改變陣元的加權系數來產生所需的天線方向圖，與陣元的相位、幅度及陣元空間分布有關。方向圖綜合可以用來形成特定形狀的主瓣，約束旁瓣電平及在指定方向產生零點。最初的波束賦形方法，是Dolph用Chebyshev多項式法來獲得等旁瓣的方向圖。在給定副瓣電平的情況下，能形成最窄主瓣寬度；在給定主瓣寬度情況下，能形成最低的旁瓣［1］。之后Taylor等人也提出了各種具有均勻旁瓣的方向圖綜合方法，又有Hyneman等提出了旁瓣電平包絡隨方向角變化的方向圖的綜合方法。但這些方法只適用于由均勻分布的各向同性陣元構成的陣列，而不能直接用于任意陣。Perini［2］以及Tseng［3］等人基于自適應陣理論提出了多種任意陣的方向圖賦形方法。后來智能優化算法如遺傳算法等被應用于方向圖綜合。Tennant［4］使用遺傳算法來控制干擾方向的零陷，Marcano［5］用遺傳算法進行線陣和平面陣的波束賦形。

多波束天線作為衛星通信系統等領域的一項重要的新技術，在近代得到了快速的發展。多波束天線是指系統同時發射多個并行波束，通過調整天線陣的權值控制每個波束的形狀與方位。多波束天線具有高增益，大覆蓋面等優勢。20世紀60年代在國外就有了關于多波束天線的研究理論，如用于多波束天線網絡的Butler矩陣。現在很多通信衛星上都使用了多波束天線，如Globalstar與Iridium通信衛星系統。

1 波束域賦形算法

波束形成的基本思想是通過將各陣元輸出進行加權求和，在同一時間內將天線陣列波束導向到一個方向上，對期望信號得到最大輸出功率的導向位置給出波達方向估計，其目的是為了增強特定方向信號的功率。

單個波束的方向圖p（θ）為［6］：

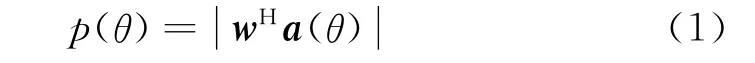
當w對某個方向θ的信號同相相加時得到p（θ）的模值最大。所謂的帶指向的方向圖，其信號的指向是通過控制加權相位來實現的，即相控陣列。

多波束形成是用多組加權系數對信號進行加權，每組加權系數在所要求的方向θk（k=1，2，…，P）上形成一個主瓣，其實質是按每個波束的指向來確定要補償的相位差，并根據各波束單元信號的幅度差異和天線副瓣要求的幅度加權系數來進行幅度調整，例如對權值加各種窗函數。這樣產生多個具有任意指向間隔的波束，每個波束指向即各波束的間距可以調整，且各個波束可因幅度加權系數不同而具有不同的波束形狀。這里加權矢量可以根據不同情況的要求而自適應的變化，也就是實現自適應的波束控制。

如果是普通多波束形成，則每一個發射波束的加權系數即為此波束的方向指向θk（k=1，2，…，P）所對應的導向矢量a（θk）。單個波束的波束寬度也即波束主瓣半功率下降點的寬度，由天線孔徑來決定。

使用多波束來實現波束域賦形，是利用多個指向間隔一定的單波束來形成一個和波束，各個單波束陣元加權值不同，使這個和波束的波束寬度比單個波束寬度有所展寬，并且和波束的增益要大于單個波束的增益。

2 仿真實驗和性能分析

仿真參數：下面的仿真中采用的陣型為4×4陣元的均勻方陣，陣元間距為半波長，陣元個數為16，通過4個單個波束來形成一個和波束。陣型結構如圖1所示，單個波束的方向圖如圖2所示。可以得出，在圖1陣型結構下產生的單波束的波束寬度為26°。

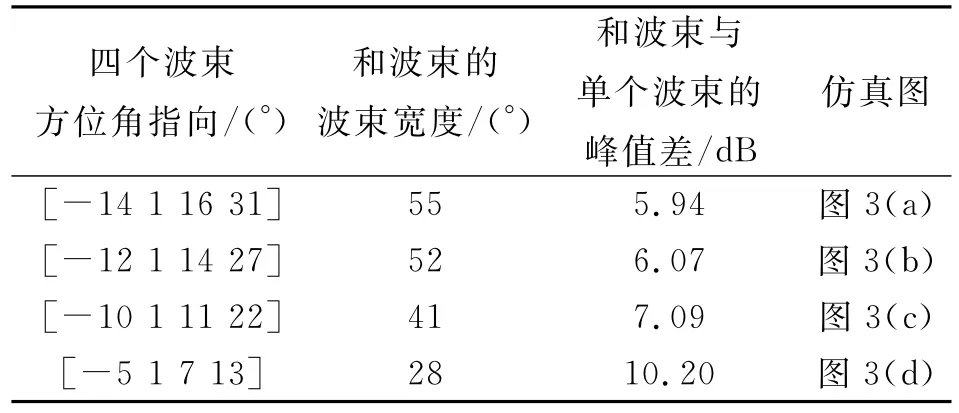
仿真實驗1：下面是用4組指向不同的多波束進行賦形的仿真實驗，為了更直觀地看出和波束形狀變化情況，這里給出方陣的切面圖，且只改變單個波束的方位角度指向。由下面的仿真圖可以看出當4個波束的方位角指向不同時，其和波束的波束形狀也不同，波束寬度和波束增益都有所改變。和波束的主瓣寬度有明顯的展寬，增益也變大。

多波束賦形的切面方向圖如圖3所示。表1列出了這4組多波束形成的和波束的波束寬度和增益改善值。

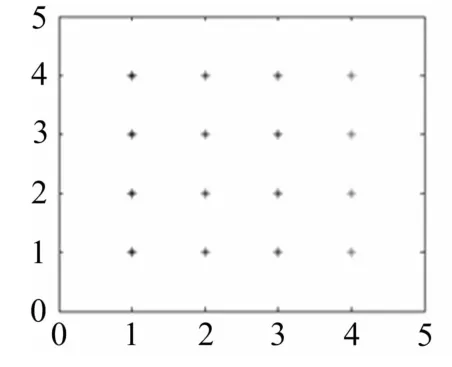
圖1 陣型結構圖

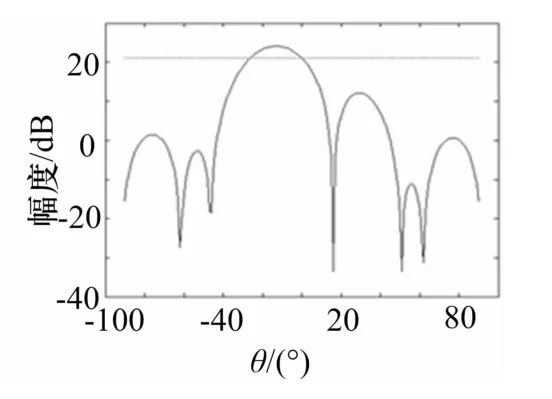
圖2 單波束的方向圖

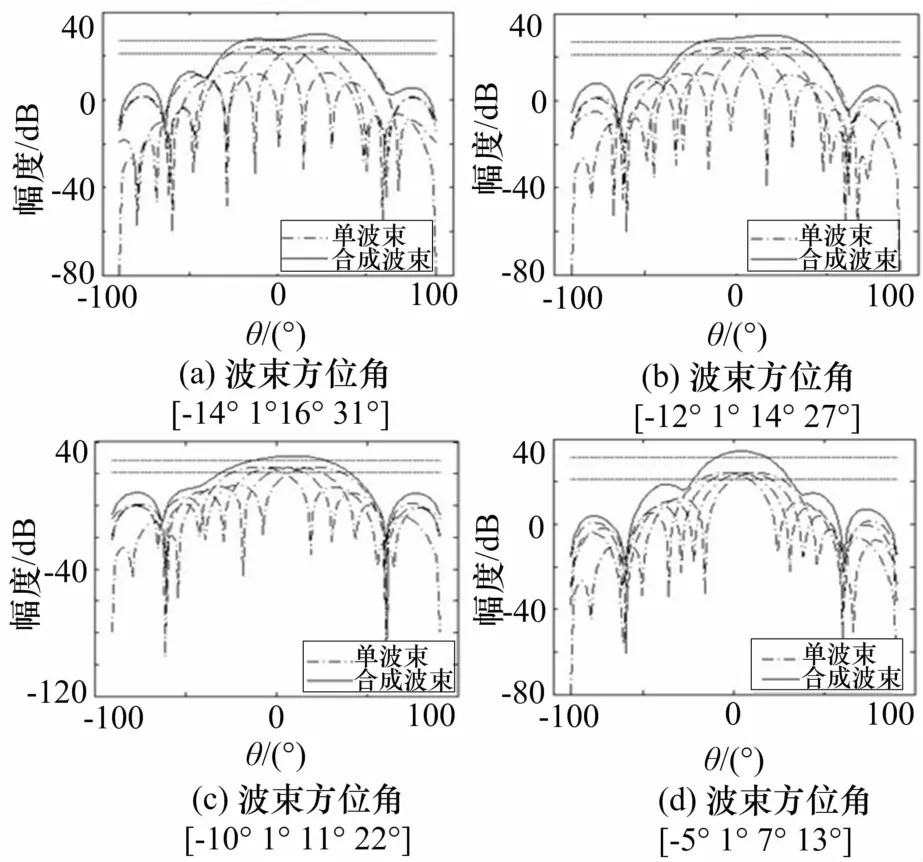
圖3 不同角度指向的多波束賦形切面方向圖

表l 多波束賦形性能參數表

仿真實驗2：下面兩組仿真是各個單波束的方位角和俯仰角指向都變化的多波束賦形三維圖，每個波束的方位角度和俯仰角度都不同。由仿真圖可以看出當4個波束的指向不同時，其和波束的波束形狀也不同，波束寬度和波束增益都有所改變。

兩組多波束賦形的三維方向圖及切面方向圖如圖4～7所示，表2列出了和波束的波束寬度和增益改善值。

由仿真實驗1和2可以看出，多波束合成可以展寬方向圖的主瓣寬度，并且增大主瓣增益。下面介紹一種使用優化算法來實現特定形狀方向圖的波束域賦形方法。

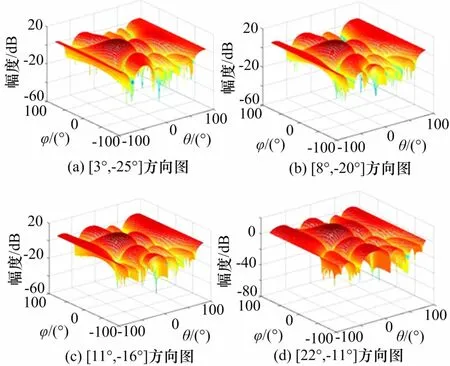
圖4 4個單波束方向圖

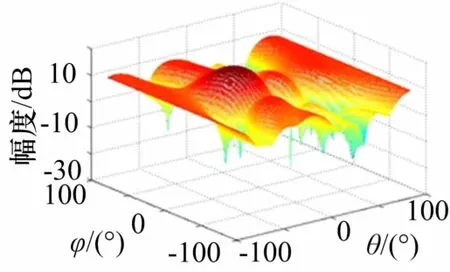
圖5 和波束方向圖

圖6 和波束的方位維切面方向圖

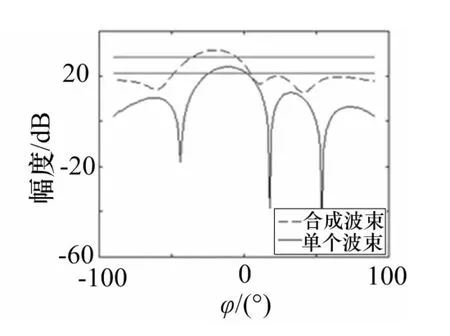
圖7 和波束的俯仰維 切面方向圖

表2 多波束賦形性能參數表

3 基于優化算法的多波束賦形算法

在雷達、通信等眾多領域中，往往需要的是具有一定的主瓣寬度、特殊的主瓣形狀和低的旁瓣電平的天線波束方向圖，例如平頂波束、余割平方波束等。上面提出的波束域的賦形方法只是簡單地展寬了主瓣寬度，沒有對主瓣形狀進行約束，這里使用一種優化算法——粒子群優化算法（PSO）［7］實現波束域賦形，先優化出單個波束的角度指向，使合成波束的波束寬度達到所需的寬度，再經過陣列天線的幅度、相位加權最后形成具有特定主瓣形狀的波束方向圖。

1）PSO算法流程，如圖8所示。

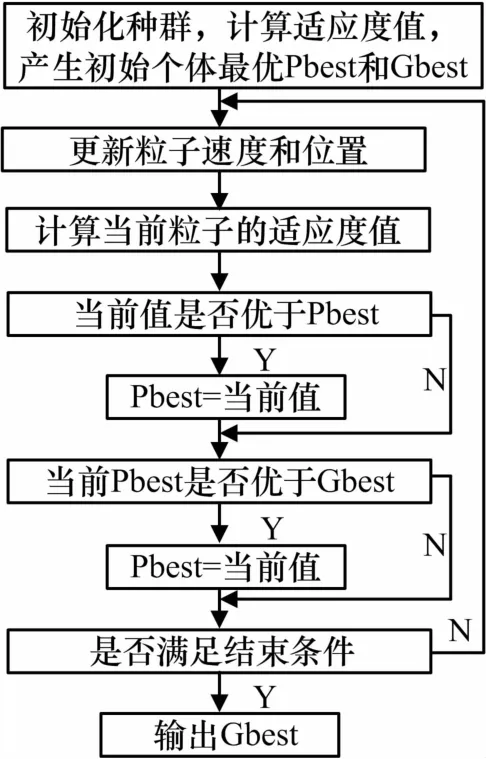
圖8 PSO算法流程圖

2）PSO算法的優點。

PSO算法和其他進化算法有很多相似之處，它們都應用到“種群”這個概念。此外，在使用適應度值來進行最優值隨機搜索時，算法的隨機性不能保證一定會搜索到最優解。這些優化算法是從一個集合開始，而不是從某一個個體開始，這樣就提高了算法的全局搜索能力，使陷入局部極小值的可能性變小，提高了優化算法的效率及性能。

但是，PSO算法與其他算法相比又有很多不同之處：具有記憶功能，粒子和種群的歷史最好位置被記憶并傳遞給其他的粒子；沒有交叉和變異運算，是通過粒子速度完成搜索的；需要調整的參數比較少，結構簡單，便于實現；用實數進行編碼，由問題的解直接來決定，問題解的變量數就是粒子的維數；收斂速度比較快，在迭代過程中只有最優粒子才把信息傳遞給其他得粒子，屬于單向信息流動。

3）基于PSO算法的多波束賦形算法。

在波束域對多波束賦形是通過兩次優化算法來實現的：

①先對各個波束的方向指向進行優化，即相位加權優化，使和波束的波束寬度達到最大值。

②再對各波束進行幅度優化，即幅度加權優化，使和波束在主瓣寬度內波束形狀保持平坦，即形成平頂波束。

在優化過程中，需要對每次優化結果的優劣做出評價，這個評價函數就為適應度函數。本文采用的多波束賦形方法要經過兩次PSO優化算法，第1次優化過程中的適應度函數fitness-angle表示和波束的3dB帶寬，經過這次的優化形成的最優和波束有最大的主瓣寬度；第2次優化的適應度函數fitness-amp為前一次得到的最優和波束主瓣寬度內的波束幅度值與期望的平頂波束的幅度差。

仿真實驗1：均勻線陣

仿真參數：仿真中采用的陣型為4陣元的均勻線陣，陣元間距為半波長，通過4個波束來形成1個和波束。一級優化的進化代數為100代，種群數為20；二級優化的進化代數為50代，種群數目為10。

經過兩級優化后，得到下面的最優結果：

4個波束指向為θ=［-19.3° -10.0° 8.9° 14.4°］；幅度加權為w=［0.36° 1.28° 0.68° 0.88°］。圖9～10給出了兩級優化后形成的方向圖與優化的適應度值收斂曲線圖。

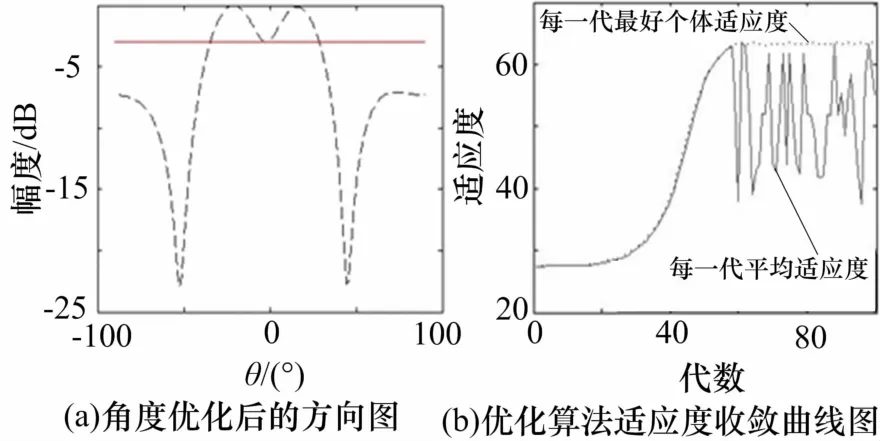
圖9 一級優化仿真圖

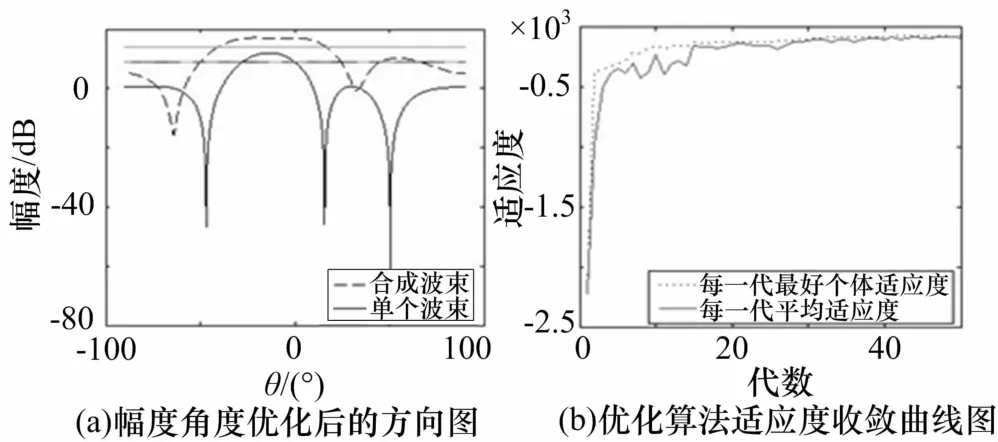
圖10 二級優化仿真圖

最終優化后形成的和波束的主瓣峰值比單波束主瓣峰值增大3.45dB，而且波束寬度達到60.3°。可見，經過兩級PSO算法優化后，合成波束的波數寬度明顯展寬，增益提高，主瓣平頂變得平坦。

仿真實驗2：均勻面陣

仿真參數：仿真中采用的陣型為4×4陣元的均勻面陣，陣元間距為半波長，通過4個波束來形成1個和波束。優化過程中的進化代數為100代，種群數為20。

經過優化后，得到下面的最優結果。

4個波束指向為：

θ=［10.4° -12.1° -12.3° 10.6°］

ψ=［13.2° 12.7°-11.1° -10.7°］

圖11～13給出了單波束的方向圖與優化后多波束賦形的方向圖，以及優化過程中的適應度值收斂曲線圖，表3列出了波束性能。

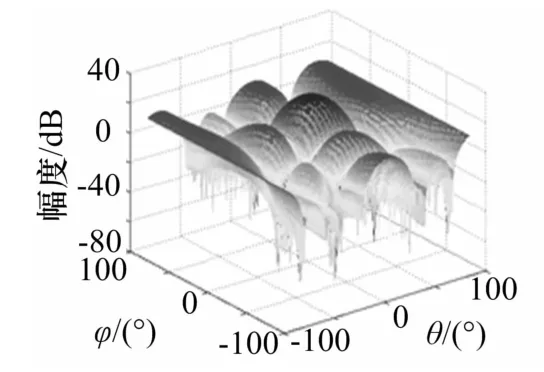
圖11 單個波束方向圖

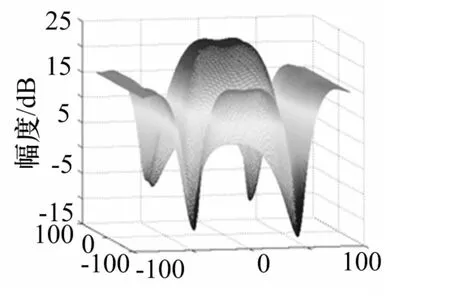
圖12 角度優化后的方向圖

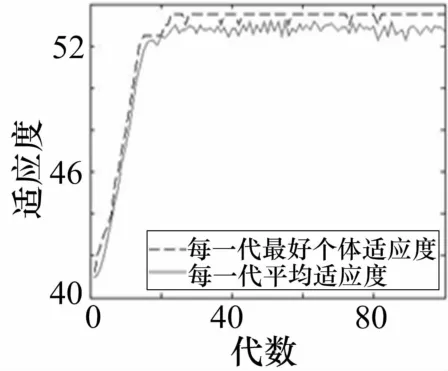
圖13 角度優化算法的適應度收斂曲線圖

表3 波束性能

可以從仿真結果得到，單波束的切面方向圖，其方位維和俯仰維3dB功率下降點的波束寬度為27°左右。而優化后的和波束的切面方向圖，其方位維和俯仰維3dB功率下降點的波束寬度分別可以達到54°和61°。最終優化后形成的和波束的方向圖主瓣峰值為23.27dB，略小于單波束主瓣峰值（為23.49dB）。可見，經過PSO算法優化后，均勻面陣陣型結構下，合成波束的波束寬度明顯展寬，增益下降不大，其主瓣平頂變得平坦。

4 結束語

本文提出了一種新的波束域賦形方法即多波束賦形方法，通過多個波束來合成一個波束，再經過優化以后，能夠實現波束域賦形，而且方向圖主瓣會展寬，增益會變大。首先介紹了多波束賦形方法的實現方式，再經過仿真實驗分析了多波束賦形算法的可實現性。仿真結果說明通過改變單個波束的指向（方位角或俯仰角），可以形成一個主瓣寬度較寬的方向圖，而且這個和波束的增益比單個波束增益有所增大。然后，借助PSO優化算法，對多個單波束進行相位和幅度的兩級優化，使合成的方向圖主瓣寬度能夠達到最大值，而且主瓣形狀也成為平頂。通過仿真實驗給出了線陣和面陣的優化效果圖和波束性能值，結果證明這種優化后的多波束賦形方法不僅實現簡單，賦形效果也很好。所以，結合已有的多波束和波束賦形技術，把多波束賦形方法引入實際應用中，不僅可行也是有效的。■

［1］ Dolph CL．A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level［J］.Proceedings of the IRE，1946，34（6）：335-348.

［2］ Perini J，Idselis M.Note on antenna pattern synthesis using numerical iterative methods［J］.IEEE Trans.on Antennas and Propagation，1971，19（2）：284-286.

［3］ Tseng CY，Griffiths LJ.A simple algorithm to achieve desired patterns for arbitrary arrays［J］.IEEE Trans.on Signal Processing，1992，40（11）：2737-2746.

［4］ Tennant A，Dawoud MM，Anderson AP.Array pattern nulling by element position perturbations using a genetic algorithm［J］.Electronics Levers，1994，30（3）：174-176.

［5］ Marcano D，Jimenez M，Duran F，et al．Synthesis of antenna arrays using genetic algorithms［C］.Proceedings of the 1995 First IEEE International Caracas Conference on Devices，Circuits and Systems，1995：328-332.

［6］ 王永良，陳輝，彭應寧.空間譜估計理論與算法［M］.北京：清華大學出版社，2004.

［7］ 孫海浪.陣列天線測向算法及子陣劃分研究［D］.西安：西安電子科技大學，2010.

A method of multi-beam shaping based on intelligent algorithm

Yang Jiamin
（No.8511 Research Institute of CASIC，Nanjing 210007，Jiangsu，China）

A kind of beam shaping algorithm is introduced in the dissertation.The multi-beamforming shaping approach is analyzed.Multi-beamforming which can be used to enhance the stability of the beam is vertified.Then through the intelligent algorithm to optimize the phase and amplitude of the multiple beams，the perfect beam pattern can be obtained.The simulation results demonstrate that the multi-beamforming shaping method can not only broaden the main lobe，but also increase the main lobe gain.The proposed beamforming algorithm is simple and well shaped.So the multi-beaming shaped method is effective and can increase the robust of beam.

adaptive beamforming；robust；multi-beamforming shaping

TN978

A

2014-08-20；2015-07-01修回。

楊佳敏（1986-），女，工程師，碩士，主要研究方向為雷達信號處理、陣列信號處理。