一種基于串聯(lián)解耦的陀螺飛輪擺角控制方法*

章曉明，李海軍

(1.上海航天控制技術(shù)研究所，上海 200233；2.上海市空間智能控制技術(shù)重點(diǎn)實(shí)驗(yàn)室，上海 200233)

?

一種基于串聯(lián)解耦的陀螺飛輪擺角控制方法*

章曉明1,2，李海軍1,2

(1.上海航天控制技術(shù)研究所，上海 200233；2.上海市空間智能控制技術(shù)重點(diǎn)實(shí)驗(yàn)室，上海 200233)

陀螺飛輪通過撓性支撐的動(dòng)量輪轉(zhuǎn)子加減速及側(cè)向擺動(dòng)實(shí)現(xiàn)三軸控制力矩輸出，飛輪轉(zhuǎn)子兩維側(cè)擺伺服系統(tǒng)是實(shí)現(xiàn)三軸力矩輸出功能的關(guān)鍵.高速轉(zhuǎn)子兩維側(cè)擺運(yùn)動(dòng)存在強(qiáng)耦合，采用常規(guī)的PID控制器無(wú)法實(shí)現(xiàn)兩通道獨(dú)立輸出控制力矩.給出了一種解耦控制方法，通過串聯(lián)解耦矩陣實(shí)現(xiàn)兩維擺角解耦控制，并通過實(shí)時(shí)計(jì)算解耦矩陣系數(shù)解決解耦矩陣隨飛輪轉(zhuǎn)子轉(zhuǎn)速時(shí)變的問題.數(shù)值仿真結(jié)果驗(yàn)證了這種解耦控制方法的有效性.

陀螺飛輪;串聯(lián)解耦;擺角控制.

0 引 言

陀螺飛輪是一種用于小衛(wèi)星姿態(tài)控制的執(zhí)行機(jī)構(gòu).它的結(jié)構(gòu)類似于兩自由度動(dòng)力調(diào)諧陀螺，即用一個(gè)兩自由度撓性支架支撐動(dòng)量轉(zhuǎn)子，撓性支架與驅(qū)動(dòng)軸固連[1].驅(qū)動(dòng)軸在電機(jī)拖動(dòng)下高速旋轉(zhuǎn)，并通過加減速在驅(qū)動(dòng)軸方向上輸出控制力矩.飛輪轉(zhuǎn)子在一個(gè)兩維力矩器作用下實(shí)現(xiàn)兩自由度側(cè)擺，通過改變飛輪動(dòng)量矩的方向在與驅(qū)動(dòng)軸垂直的平面內(nèi)輸出兩軸控制力矩.因此陀螺飛輪是一種可以實(shí)現(xiàn)三軸力矩輸出的執(zhí)行機(jī)構(gòu).一臺(tái)陀螺飛輪可以同時(shí)實(shí)現(xiàn)一臺(tái)偏置動(dòng)量飛輪和兩臺(tái)零動(dòng)量反作用飛輪的功能，其自旋軸角動(dòng)量為整星提供偏置角動(dòng)量，并通過電機(jī)加減速(飛輪工作模式)以及轉(zhuǎn)子有限轉(zhuǎn)角側(cè)擺運(yùn)動(dòng)(力矩陀螺工作模式)吸收環(huán)境干擾力矩.由于小衛(wèi)星受到的干擾力矩較小，動(dòng)量輪小范圍內(nèi)的側(cè)擺運(yùn)動(dòng)即可滿足小衛(wèi)星對(duì)動(dòng)量輪角動(dòng)量吸收能力的要求.

國(guó)內(nèi)外對(duì)陀螺飛輪的研究開始于20世紀(jì)90年代.1999年Tyc等[2]在第十三屆美國(guó)AIAA會(huì)議上提出陀螺飛輪的構(gòu)想，同時(shí)他們?cè)跁?huì)議上還宣告其樣機(jī)已研制成功并闡述了其工作原理.隨后Walkty等[3]對(duì)陀螺飛輪的動(dòng)力學(xué)建模進(jìn)行了敘述和分析.運(yùn)用復(fù)數(shù)域分析法對(duì)經(jīng)典控制算法(根軌跡法和頻域分析法)進(jìn)行改進(jìn)，用于陀螺飛輪復(fù)系數(shù)模型分析，提出了陀螺飛輪系統(tǒng)的設(shè)計(jì)方案.該方案采用固定系數(shù)校正網(wǎng)絡(luò)實(shí)現(xiàn)飛輪轉(zhuǎn)子側(cè)擺運(yùn)動(dòng)控制，未考慮高速飛輪轉(zhuǎn)子在側(cè)擺過程中的解耦問題及控制系統(tǒng)參數(shù)隨飛輪轉(zhuǎn)速改變而引起的變化[4].

本文在對(duì)陀螺飛輪擺角控制時(shí)變模型建模和分析基礎(chǔ)上，提出了一種數(shù)字式串聯(lián)解耦控制器設(shè)計(jì)方法，并通過數(shù)值仿真驗(yàn)證了這種解耦控制方法的有效性.

1 陀螺飛輪擺角控制模型

1.1 控制對(duì)象

陀螺飛輪結(jié)構(gòu)如圖1所示，擺角伺服系統(tǒng)包括撓性框架支撐的轉(zhuǎn)子、兩維力矩器、兩維擺角傳感器.撓性框架支撐的飛輪轉(zhuǎn)子可實(shí)現(xiàn)兩維側(cè)擺，擺角范圍±4°；兩維擺角傳感器利用變磁阻原理檢測(cè)其兩維擺角作為反饋信號(hào)[5]；兩維力矩器依據(jù)反饋控制信號(hào)對(duì)飛輪體施加控制力矩實(shí)現(xiàn)側(cè)擺伺服控制.

1.2 控制對(duì)象傳遞函數(shù)

陀螺飛輪轉(zhuǎn)子的動(dòng)力學(xué)方程可寫為[5]

(1)

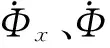
(2)

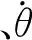
對(duì)式(1)進(jìn)行拉式變換可以得到陀螺飛輪兩維擺角與力矩器控制力矩及殼體角速度之間的傳遞函數(shù)矩陣(3).其中K、H是轉(zhuǎn)子轉(zhuǎn)速的函數(shù)，該系統(tǒng)是一個(gè)時(shí)變系統(tǒng).

(3)

在系統(tǒng)開環(huán)條件下，轉(zhuǎn)子側(cè)擺運(yùn)動(dòng)表現(xiàn)出明顯的耦合現(xiàn)象.圖2是轉(zhuǎn)子對(duì)一個(gè)通道控制力矩的開環(huán)響應(yīng)特性曲線.從圖示曲線可以明顯看出其耦合特性及隨轉(zhuǎn)子轉(zhuǎn)速變化的特性.

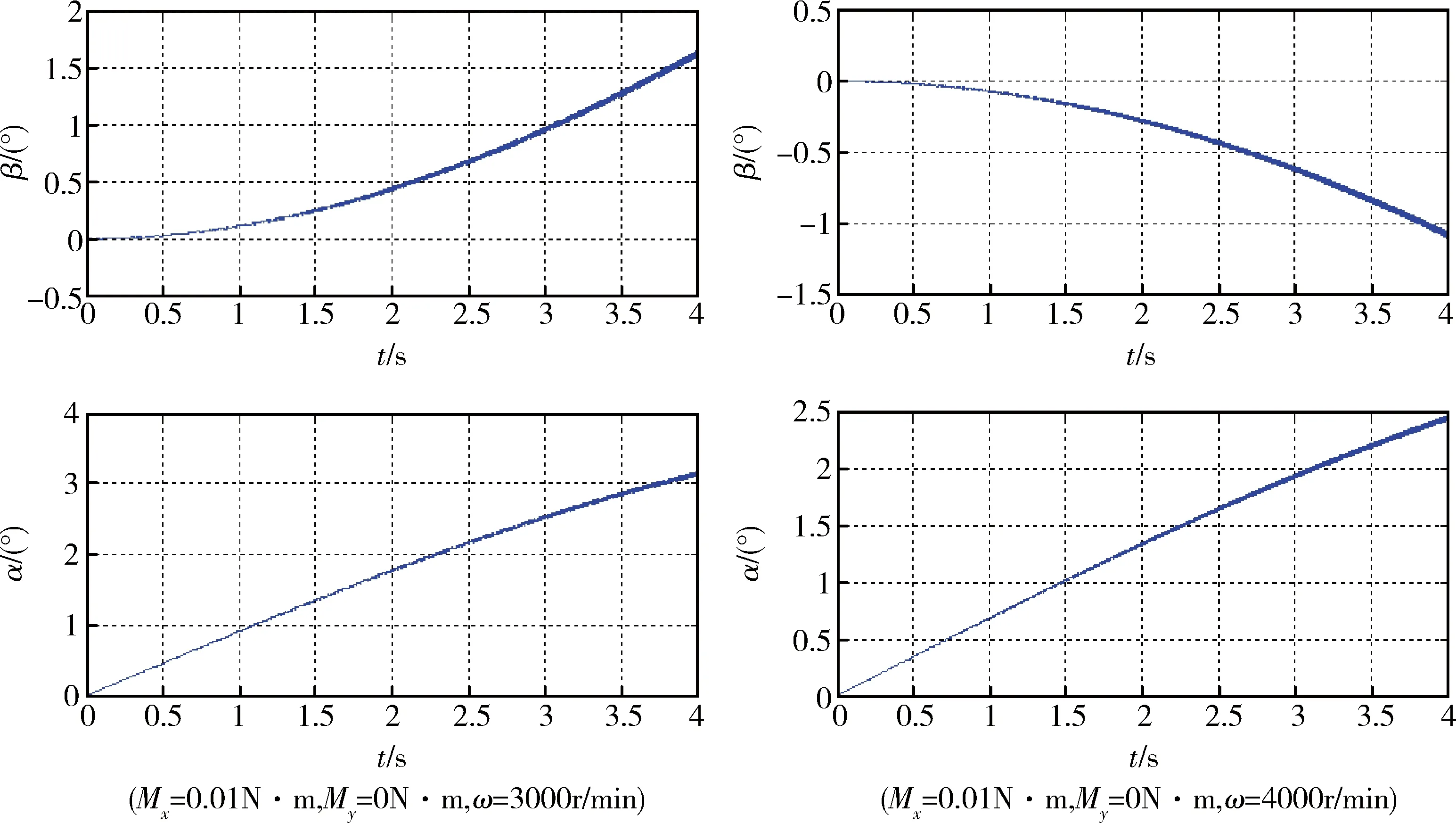
圖2 陀螺飛輪擺角開環(huán)響應(yīng)特性Fig.2 Swing angle characteristic under aopen-loop control

2 串聯(lián)解耦控制器設(shè)計(jì)

定義

(4)

則式(3)可以寫為式(5)

(5)

式(5)中與力矩器輸出力矩相關(guān)的傳遞函數(shù)是系統(tǒng)的可控部分，與外界角速度相關(guān)的傳遞函數(shù)是系統(tǒng)不可控部分.可控部分的傳遞函數(shù)矩陣存在耦合項(xiàng).為了實(shí)現(xiàn)兩維擺角控制，希望通過一個(gè)矯正網(wǎng)絡(luò)使該動(dòng)態(tài)過程解耦，這樣就可以將一個(gè)兩輸入、兩輸出的耦合系統(tǒng)簡(jiǎn)化為兩個(gè)單輸入、單輸出系統(tǒng)，在此基礎(chǔ)上進(jìn)行綜合設(shè)計(jì).使用前饋補(bǔ)償器解耦是較簡(jiǎn)單的方法，只需要在待解耦系統(tǒng)的前面串接一個(gè)前饋補(bǔ)償器，使串聯(lián)組合系統(tǒng)的傳遞函數(shù)成為對(duì)角的有理函數(shù)矩陣，即可實(shí)現(xiàn)系統(tǒng)解耦.

設(shè)解耦后的系統(tǒng)傳遞函數(shù)矩陣為N(s)，前饋補(bǔ)償傳遞函數(shù)矩陣為M(s)，取

M(s)=G-1(s)N(s)

(6)

則該前饋環(huán)節(jié)與原系統(tǒng)串聯(lián)

G(s)M(s)=G(s)G-1(s)N(s)=N(s)

(7)

即可獲得所要的解耦系統(tǒng).對(duì)(4)式求逆得到

(8)

并設(shè)解耦后的系統(tǒng)為一個(gè)Ⅱ型系統(tǒng)(9)，這樣就可以常值偏角跟蹤常值角加速度輸入，以零偏角跟蹤常值角速度輸入.

(9)

式(8)、(9)代入式(6)得到所求的解耦矩陣

(10)

解耦后系統(tǒng)的極點(diǎn)為0，是一個(gè)臨界穩(wěn)定系統(tǒng)，需要串聯(lián)控制器才能保證系統(tǒng)穩(wěn)定.控制器Gc(s)采用常規(guī)的PID矯正網(wǎng)絡(luò)，其形式為

Mx(s)=kpβ(s)+kdsβ(s)+kiβ(s)/s，

My(s)=kpα(s)+kdsα(s)+kiα(s)/s

(11)

最終的控制器可由一個(gè)PID矯正網(wǎng)絡(luò)加一個(gè)串聯(lián)解耦網(wǎng)絡(luò)組成，其系統(tǒng)框圖見圖3.

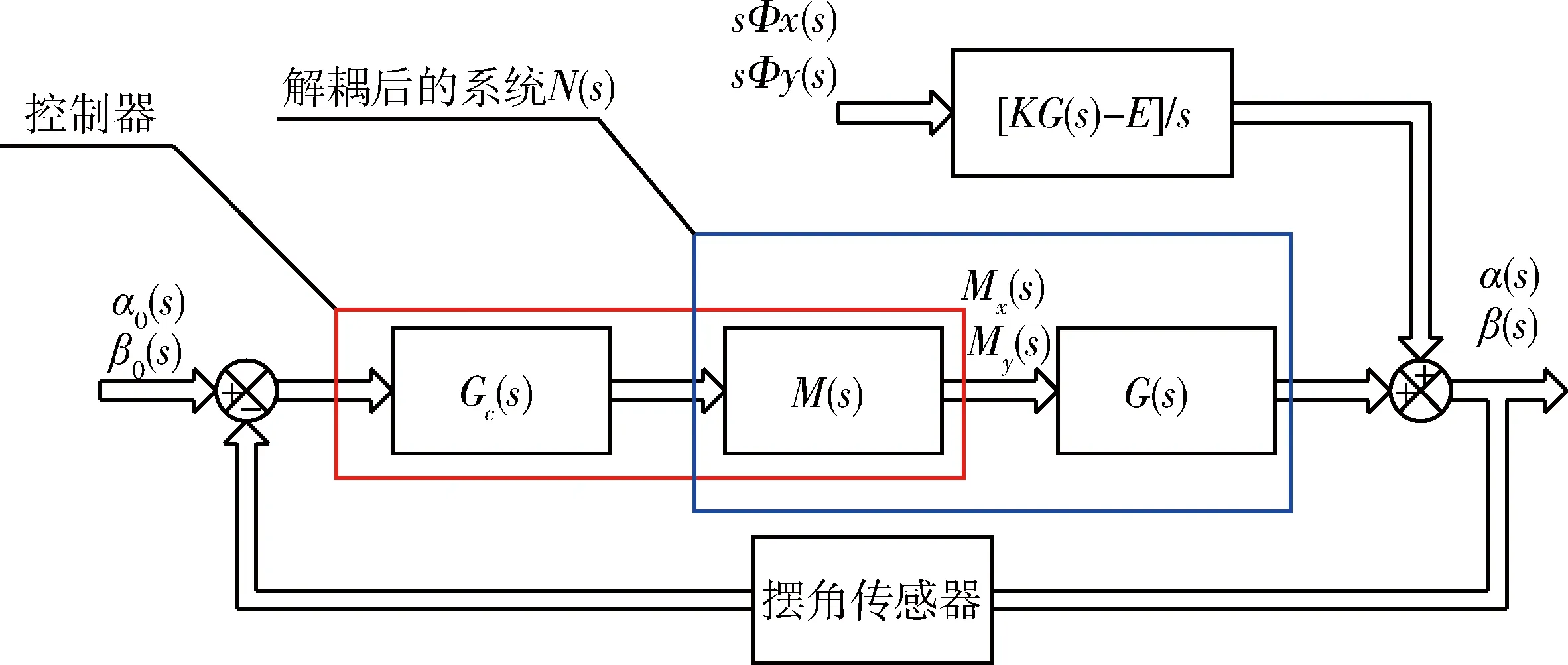
圖3 串聯(lián)解耦控制器框圖Fig.3 Series system for decoupling control

3 系統(tǒng)時(shí)變性的解決方法

式(9)給出的解耦矩陣包含時(shí)變項(xiàng)K(剩余剛度)和H(轉(zhuǎn)子角動(dòng)量)，它們是轉(zhuǎn)子轉(zhuǎn)速的函數(shù).為了實(shí)現(xiàn)系統(tǒng)解耦，必須根據(jù)飛輪轉(zhuǎn)速實(shí)測(cè)值在線更新解耦矩陣系數(shù).這種控制方法可以用數(shù)字控制器實(shí)現(xiàn)，圖4給出了數(shù)字控制器的執(zhí)行流程圖.

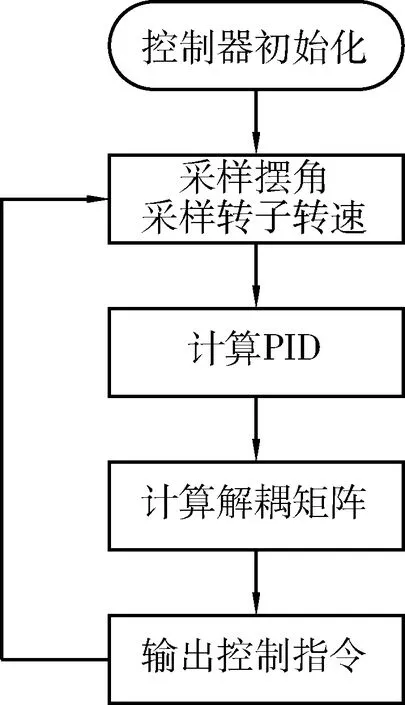
圖4 數(shù)字控制器計(jì)算流程圖Fig.4 Numeric controller flow chart

K和H的計(jì)算需要用到轉(zhuǎn)子極轉(zhuǎn)動(dòng)慣量、赤道轉(zhuǎn)動(dòng)慣量、平衡環(huán)極轉(zhuǎn)動(dòng)慣量、赤道轉(zhuǎn)動(dòng)慣量.對(duì)一個(gè)實(shí)際的陀螺飛輪，這些慣量值是常量，通過CAD軟件可以給出精確的設(shè)計(jì)值.通常陀螺飛輪這類精密的執(zhí)行機(jī)構(gòu)，其零部件經(jīng)過精密加工制造而成，因此部件實(shí)際慣量值與設(shè)計(jì)值的偏差對(duì)閉環(huán)控制系統(tǒng)而言是可接受的.

圖5 擺角解耦控制仿真曲線Fig.5 Swing angle characteristic under a close-loop control

4 解耦控制算法驗(yàn)證

針對(duì)某型陀螺飛輪的設(shè)計(jì)參數(shù)，采用本文設(shè)計(jì)的解耦矩陣進(jìn)行數(shù)值計(jì)算驗(yàn)證解耦算法.計(jì)算參數(shù)為：

平衡環(huán)慣性張量

(12)

轉(zhuǎn)子慣性張量

(13)

撓性框架剛度系數(shù)Kp=0.56(N·m)/rad，PID控制器采用常規(guī)的Ziegler-Nichols整定方法確定，兩個(gè)通道采用同樣的參數(shù)：kp=100,kd=0.1,ki=10.

圖5是一組典型的仿真結(jié)果，仿真工況為飛輪轉(zhuǎn)子轉(zhuǎn)速?gòu)? 000 r/min加速至3 500 r/min；同時(shí)，對(duì)轉(zhuǎn)子兩維擺角伺服系統(tǒng)輸入階躍指令，使其分別在兩個(gè)擺動(dòng)方向上偏轉(zhuǎn)4°并保持穩(wěn)定.圖中給出了擺角響應(yīng)特性及力矩器輸出力矩特性.在前1 s內(nèi)，轉(zhuǎn)子擺角從0°位移動(dòng)到4°，此后在4°位置上保持穩(wěn)定.力矩器輸出力矩在前1 s內(nèi)經(jīng)歷一個(gè)動(dòng)態(tài)過程，而后保持常值，該常值力矩用于平衡撓性框架在高轉(zhuǎn)速下產(chǎn)生的動(dòng)力反彈性力矩，使轉(zhuǎn)子穩(wěn)定地繞傾斜軸線旋轉(zhuǎn).從圖中曲線可知，采用本文設(shè)計(jì)的解耦控制算法較好地實(shí)現(xiàn)了高速轉(zhuǎn)子兩維擺角解耦控制，在時(shí)變參數(shù)條件下能夠?qū)崿F(xiàn)系統(tǒng)解耦及穩(wěn)定控制.

5 結(jié) 論

陀螺飛輪高速轉(zhuǎn)子兩維擺角伺服控制系統(tǒng)的傳遞函數(shù)是一個(gè)雙輸入、雙輸出時(shí)變系統(tǒng)，兩個(gè)通道存在較明顯的耦合效應(yīng)，采用常規(guī)的單通道PID控制器無(wú)法實(shí)現(xiàn)兩維擺角獨(dú)立控制.本文采用串聯(lián)解耦方法設(shè)計(jì)了一種解耦網(wǎng)絡(luò)，采用該校正網(wǎng)絡(luò)將陀螺飛輪高速轉(zhuǎn)子兩維擺角的傳遞函數(shù)改造為兩個(gè)相互獨(dú)立的單輸入單輸出系統(tǒng)，串聯(lián)解耦后再采用常規(guī)的PID控制器實(shí)現(xiàn)系統(tǒng)穩(wěn)定控制.考慮到兩維擺角控制對(duì)象的傳遞函數(shù)是飛輪轉(zhuǎn)子自旋轉(zhuǎn)速的函數(shù)，可以通過實(shí)時(shí)計(jì)算解耦矩陣系數(shù)來消除解耦矩陣隨飛輪轉(zhuǎn)子轉(zhuǎn)速時(shí)變的問題.最后通過一組典型工況下的數(shù)值仿真結(jié)論驗(yàn)證了解耦控制方法的可行性.

[1] TYC G, STALEY DA,虎剛.陀螺飛輪——一種用于航天器三軸姿態(tài)控制的新型執(zhí)行機(jī)構(gòu)/敏感器[J].控制工程,2001(3):32-40.

[2] TYC G, STALEY D A, WHITEHEAD W R, et al. Gyrowheel-an gyrowheel an innovative new actuator/sensor for 3 axis spacecraft attitude control[C]//Proceedings of the 13thAnnual AIAA/USU Conference on Small Satellites.Washington D.C.:AIAA,1999:1-13.

[3] WALKTY I, PETERSEN J, DOHERTY T, et al. SCISAT-1 ACE mission C&DH unit development[C]//Proceeding of 14thAnnual/USU Conference on Small Satellites.2000:1-13.

[4] HARRISON P T.Development and testing of a GyroWheel based control system for the SCISAT-1 scientific satellite[M].[S.l.]:[s.n.],2004.

[5] 劉希珠，雷田玉.陀螺力學(xué)基礎(chǔ)[M].北京：清華大學(xué)出版社.1987:200-201

A Control Method of Gyrowheel’s Swing Angle Based on Series Decoupling

ZHANG Xiaoming1,2， LI Haijun1,2

(1.ShanghaiInstituteofSpaceflightControlTechnology，Shanghai200233,China；2.ShanghaiKeyLaboratoryofSpaceIntelligentControlTechnology，Shanghai200233,China)

A gryowheel can output torques in three directions via changing the angular momentum’s amplitude or direction. The servo system for swing angle control is the key to achieving the function of triaxial torque output. There is a strong coupling between the high-speed rotor’s swings in two directions so that the output torques in two directions independently is unavailable under normal PID control methods. A method for decoupling control is provided via adding a series of system matrices and creating two decoupling systems. The coefficients of the series of system matrices are changing as rotor speed changing. It can be solved by calculating the coefficients in a real time digital control processor. Numerical simulation result shows the feasibility of this control method.

gyrowheel； series decoupling； swing angle control

*國(guó)防科工局民用航天預(yù)先研究課題資助項(xiàng)目.

2015-03-12

V448

A

1674-1579(2015)05-0023-05

10.3969/j.issn.1674-1579.2015.05.005

章曉明(1983—)， 工程師，專業(yè)：機(jī)械設(shè)計(jì)制造及其自動(dòng)化，研究方向：空間執(zhí)行機(jī)構(gòu)研究；李海軍(1980—)，高級(jí)工程師，專業(yè)：導(dǎo)航，制導(dǎo)與控制，研究方向：飛行器控制與導(dǎo)航.