多級齒輪傳動系統關鍵參數對響應的影響分析*

胡 鵬， 王奇斌， 張義民

(東北大學機械工程與自動化學院 沈陽，110819)

多級齒輪傳動系統關鍵參數對響應的影響分析*

胡 鵬， 王奇斌， 張義民

(東北大學機械工程與自動化學院 沈陽，110819)

為了研究數控刀架中動力齒輪傳動系統運行的平穩狀況，建立了考慮時變剛度、齒側間隙的多級齒輪系統非線性動力學模型，并對方程組進行無量綱化處理。對時變嚙合剛度進行了較精確的求解，并考慮了變位系數對剛度值的影響。將齒側間隙引起的分段位移函數等效簡化成一個含雙曲正切的表達式，避免了迭代過程中的判斷問題。采用4階Runge-Kutta法對方程進行Matlab編程求解，分析了剛度展開項波動幅值、載荷力矩以及側隙對響應的影響。通過分析可知：較小的剛度展開項波動幅值對系統的平穩性有利；重載下的系統發生跳躍現象的臨界轉速變大，而工作轉速通常低于臨界轉速，從而提高了運轉的平穩性；側隙較小時易產生雙邊沖擊，產生較大噪音。

時變剛度; 齒側間隙; 非線性模型; 多級齒輪; 跳躍現象

引 言

齒輪傳動系統結構緊湊，傳動效率高，被廣泛應用于工業機械領域，如汽車變速箱、飛機發動機以及精密數控加工機床。保證傳動平穩性，降低運行過程中的噪音，一直是國內外學者研究重點。對于單齒對嚙合系統，Li等[1]提出了一個考慮摩擦的單齒對嚙合模型，采用數值方法對系統動力學特性進行仿真，分析了工作狀況、表面粗糙度和潤滑條件對系統的影響。文獻[2-3]研究了存在摩擦、間隙及時變剛度等因素的齒輪非線性動力學模型，采用數值法對響應進行了分析。王彥剛等[4]借鑒混沌振子檢測理論中根據系統相軌變化檢測信號的原理，分析了單齒故障沖擊信號出現的成因及其出現故障后非線性特性的變化。在單齒輪副的研究基礎上，李發家等[5]研究了行星齒輪傳動系統的非線性動力學模型，采用數值法求解，繪制出相圖及頻譜圖，并得到齒根應力的動載荷應變圖。多級齒輪由于影響因素較多，研究相對受限，文獻[6-8]以二級齒輪傳動系統為模型，采用諧波平衡法對模型進行求解，并與數值解法進行了比較，分析了系統主要參數對動力學特性的影響。Lin等[9]研究了時變剛度非線性的二級惰輪系統動力學特性，對剛度波動項、嚙合頻率及嚙合相位的影響做了全面的分析。Liu[10]給出了多級齒輪系統的多個模型，通過解析法及有限元法對每個模型進行相應的求解，研究了不同轉速下的動態傳遞誤差的均方根值，并對跳躍現象的產生進行了說明。

筆者以數控刀架中二級齒輪傳動為模型，考慮系統存在的靜態傳遞誤差、時變剛度和齒側間隙，同時對非線性分段函數進行等效轉化，采用4階變步長Runge-Kutta法對扭振模型進行動力學求解。考慮模型中剛度、側隙、外載荷的變化，求出相應值下的動力學響應的均方根值(root-mean-square,簡稱RMS)及均值，分析得到有利于系統工作的參數值，為工程應用中的系統改進提供必要的理論依據。

1 惰輪系統的動力學模型

1.1 物理模型的建立

二級齒輪傳動包括中間軸傳動(4個齒輪)和惰輪傳動(3個齒輪)兩種情況。筆者研究惰輪傳動情形，為了便于動力學分析，給定以下假設：a.支撐軸和軸承均為剛體，即在任何方向上均無變形，保證齒輪只做扭轉運動；b.齒輪與軸剛性連接，且齒輪坯是剛性的，只有齒在嚙合方向上產生變形，用嚙合剛度表示；c.齒輪的嚙合阻尼值假定為常數，且不受側隙引起的非線性影響。

基于以上假設，惰輪系統的動力學模型如圖1所示。

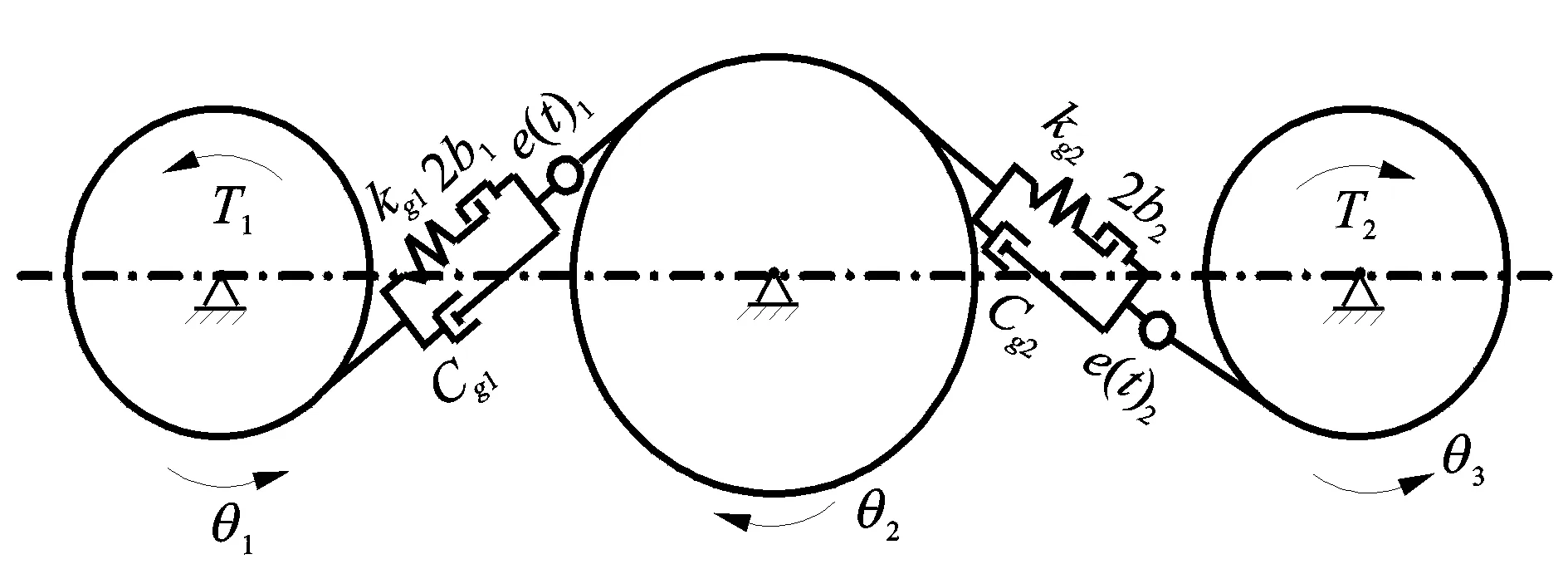
圖1 惰輪系統的動力學模型Fig.1 Dynamic model of idler gearsets

圖1中，T1和T2分別為激振扭矩和負載扭矩，每個齒輪的轉動慣量為Ji，基圓半徑為Rbi，θi(i=1～4)為齒輪的旋轉角度。第i個齒輪的旋轉角度θi為Ωit，其中Ωi為齒輪的轉速(rad/s)。kg1(t)和kg2(t)分別為一級和二級傳動的時變嚙合剛度，對應的阻尼值為Cg1和Cg2，且嚙合剛度和阻尼作用在嚙合線方向上。位移激勵e1(t)和e2(t)為各級傳動的靜態傳遞誤差。同一級傳動類似，齒輪側隙引起的非線性以分段線性的“死區”類型函數g1(t)和g2(t)來表示，側隙大小分別為2b1和2b2。

1.2 動力學方程的給定與無量綱化

基于上述假設前提和圖1的動力學模型，得到具有時變嚙合剛度、傳動誤差和側隙的微分方程，并采用相對位移作為響應量

(1)

其中：q1(t)和q2(t)為動態傳遞誤差和靜態傳遞誤差的差值。

q1(t)和q2(t)表示如下

g1(t)和g2(t)為側隙引起的分段函數，定義如下

對方程組(1)進行無量綱化處理

其中：k1m和k2m為嚙合剛度的均值部分。

進一步，假定無量綱時間變量τ=ωct，其中ωc為特征頻率(可以取Ω11)，然后令ωij=Ωij/ωc(i,j=1,2)，pi(t)=qi(t)/bc，εi(t)=ei(t)/bc，di=bi/bc(i=1,2)，其中bc為特征長度(取半側隙長度b1)，則轉換后的無量綱方程組表示如下

(2)

其中:

2 動力學模型中的參數分析

2.1 側隙引起的分段函數

函數Gi(τ)表示了嚙合過程中可能出現的3種嚙合狀態：a.pi(τ)>di，齒對正面嚙合，即無沖擊嚙合；b.|pi(τ)|≤di，脫齒，即產生單邊沖擊；c.pi(τ)<-di，齒對背面接觸，即產生雙邊沖擊。假定模型中的半齒側間隙b1=b2，即d1=d2=1，則其3種嚙合狀態的示意圖如圖2所示。

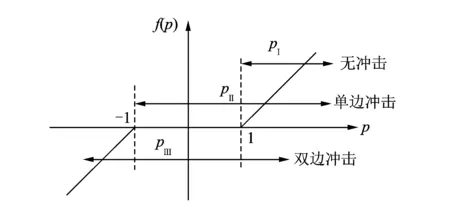
圖2 齒輪嚙合狀態示意圖Fig.2 The diagram of gear meshing state

上述分段函數在數值計算過程中存在條件判斷，為了簡化計算，可以用文獻[11]中的雙曲正切函數近似代替

其中：f(pi±1)為雙曲正切函數f(x)=xtanh(σx)。

近似精度主要取決于正則化因子σ的取值，當σ取較小值時可以減少計算時間和提高仿真結果的收斂性；當σ取較大值時與原非線性函數能更好的逼近；當σ非常大時(例如106)，逼近結果在一些文獻中體現非常好，但其對響應的巨大影響會引起數值的不穩定，尤其是本研究中的強非線性函數。圖3為對σ取不同值進行仿真的結果，取σ=200擬合精度較高。

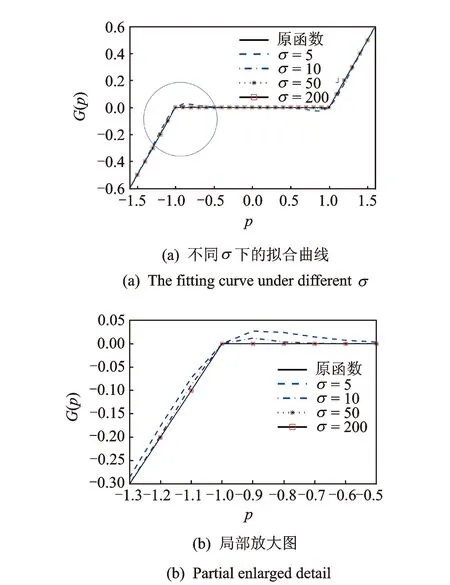
圖3 分段線性函數的近似平滑曲線Fig.3 The approximate curve of piecewise linear function

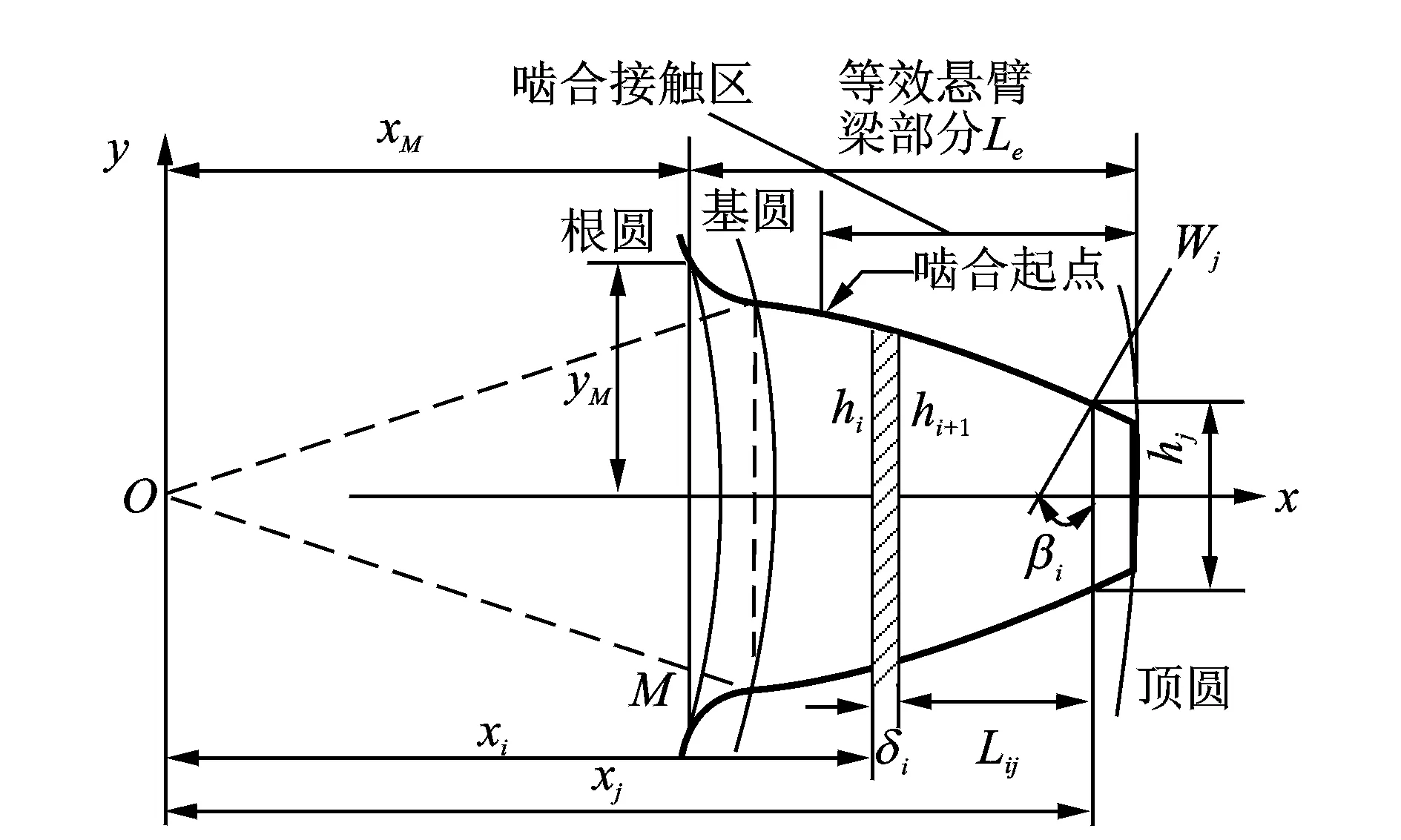
圖4 輪齒變形的計算模型Fig.4 The computational model of the gear deformation

2.2 時變嚙合剛度

輪齒可簡化為由彈性基體固支的非均勻懸臂梁，如圖4所示，其等效長度為Le，即基點M到頂圓的距離。設微元i的厚度為δi，長度取兩側齒厚的均值(hi+hi+1)/2，Lij為微元i與載荷作用點j之間在x軸方向上的距離，βj為Wj和y軸的夾角。通過建立齒輪的精確齒廓，考慮變位系數的影響，結合文獻[12]計算齒對的嚙合剛度。

給定惰輪系統的齒輪基本參數，如表1所示。

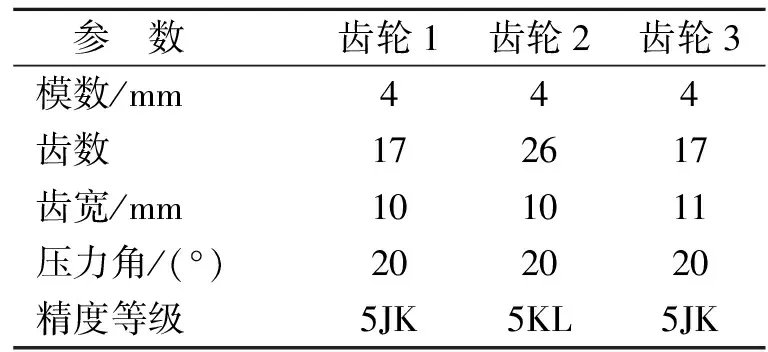
表1 齒輪傳動系統的基本參數

給出基于文獻[12]的不同變位系數情況下剛度的Matlab計算結果，如圖5所示。變位系數分別取χ1=χ2=χ3=0和χ1=χ3=0.504 7，χ2=0。兩種情況下計算結果與威伯-班納斯切克的國際標準化組織(internationalorganizationforstandardization,簡稱ISO)公式求解相近。

圖5 變位系數對嚙合剛度的影響Fig.5 Effect of the modification coefficient on mesh stiffness

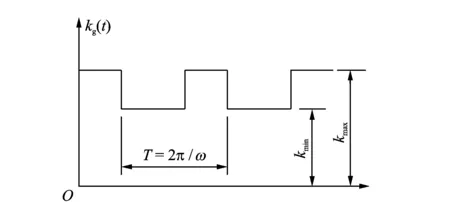
圖6 等效周期變化的嚙合剛度Fig.6 Equivalent periodic changed mesh stiffness

時變嚙合剛度主要是由于嚙合過程中出現單雙齒交替嚙合(重合度1<ε<2)產生的，為了簡化計算，可以將嚙合剛度等效為如圖6所示的矩形波形式。

進一步將嚙合剛度以嚙合頻率進行傅里葉級數展開，得到

其中：i=1,2。

參數Ωm為齒輪副的嚙合基率

Ωm=2πn1z1/60

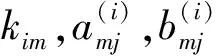
2.3 齒廓綜合誤差與側隙

齒廓綜合誤差的定義為實際齒廓沿法向偏離理論漸開線齒廓的距離，主要是在加工和安裝過程中造成的。在動力學模型中將齒廓綜合誤差看作周期性的位移激勵，以嚙合頻率作為基頻將其進行傅里葉級數展開，保留1階項，得到如下結果

其中：i=1,2；Ωe為嚙合頻率，且Ωe=Ωm；e0為常數項；Aie為1階諧波幅值；φ為相位角。

對于造成系統強非線性的齒側間隙2b值的大小主要取決于齒輪的精度等級。

3 動力學模型的數值分析

齒輪的基本參數見表1，驅動力矩為35 Nm，負載力矩為35 Nm；嚙合剛度的均值k1m和k2m分別為1.879×108N/m和1.863×108N/m；齒側間隙值b1=b2=50 μm；令e0的值為0，A1e=10 μm，A2e=12 μm。采用4階變步長Runge-Kutta法進行動力學數值求解，分析響應的無量綱均方根值RMS(減去均值后)與均值在不同參數值下隨轉速變化的波動趨勢。

3.1 嚙合剛度對響應的影響

對嚙合剛度進行傅里葉級數展開時，保留的嚙合剛度項R較大時，其響應結果中會出現超諧波共振；而當R=1，響應結果中不會出現此現象。取Λ為無量綱嚙合頻率，ωn1和ωn2為無量綱固有頻率，圖7中在Λ=1/3ωn1=0.271和Λ=1/2ωn1=0.407處出現了超諧波共振。當嚙合頻率值Λ=0.47和Λ=0.68時，系統無量綱響應的RMS幅值出現跳躍現象。

圖7 剛度項R=1和R=3時無量綱響應的RMS值(減去均值)Fig.7 While R=1 and R=3, the RMS of dimensionless response(minus average)

圖8給出了響應p1(τ)和p2(τ)的均值，可以看到當R取1和3時，對響應均值無影響，兩齒對的均值基本重合。圖8中的直線部分表示嚙合過程中隨著嚙合頻率的增大均值不變，即當Λ<0.47時，沒有發生脫齒現象。當Λ>0.47時，p1m和p2m發生明顯的波動，這是由于在嚙合過程中出現了脫齒現象，產生單邊沖擊。結合圖7中的RMS值可以看出，由于波動幅值小于齒側間隙，嚙合過程中沒有出現雙邊沖擊。

圖9 剛度1階諧波分量對無量綱響應RMS值的影響Fig.9 Influence of the harmonic stiffness on RMS of dimensionless response

圖10 扭矩對無量綱響應RMS值的影響Fig.10 Influence of torques on RMS of dimensionless response

3.2 力矩對響應的影響

當剛度展開項取R=3，扭矩T1分別取35,60,100 Nm時，由圖10可知，隨著載荷的增大，系統仍無法避免脫齒現象的發生。均方根值p1rms和p2rms的曲線形狀依舊相同，但整體的幅值隨載荷的增大而增大。系統因單邊沖擊而發生跳躍現象的嚙合頻率點逐漸增大，即發生跳躍的轉速增大，沒有發生雙邊沖擊。當T1取不同值時，跳躍產生的嚙合頻率分別為Λ=0.47，Λ=0.54，Λ=0.6，對應的齒輪的轉速分別為11 860，13 626和15 140 r/min。設計過程中要避免在工作轉速下產生跳躍現象，因為這會降低系統的運作平穩性。

3.3 齒側間隙對響應的影響

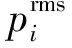
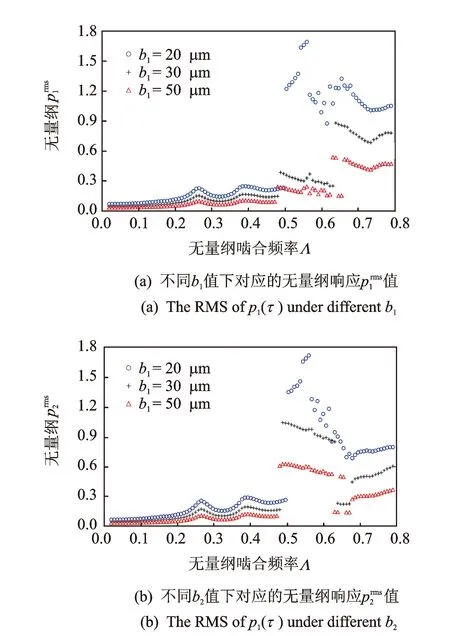
圖11 側隙大小對無量綱響應RMS值的影響Fig.11 Influence of the backlash value on the RMS of dimensionless response

圖12 側隙大小對無量綱響應均值的影響Fig.12 Influence of the backlash value on the mean value of dimensionless response

4 結 論

1) 由于工作轉速通常低于10 kr/min，所以系統參數在工作轉速范圍內不會產生雙邊沖擊現象。

2) 嚙合剛度項保留階數較多時，嚙合過程中會出現超諧波共振，同時響應的振動幅值隨嚙合剛度展開項幅值增大而增大。

3) 當扭矩T1取值逐漸增大時，系統發生跳躍的嚙合頻率點也逐漸增大，分別為0.47，0.54，0.6，即在重載下系統發生跳躍的臨界轉速變大。由于工作轉速低于臨界轉速，這可以保證運轉的平穩性。

4) 取較小的齒側間隙會增加系統產生雙邊沖擊的幾率，而雙邊沖擊會使系統運轉平穩性下降，同時還會產生噪音，設計過程中在保證齒輪精度的同時要合理選取齒側間隙。

[1] Li Sheng, Kahraman A. A tribo-dynamic model of a spur gear pair[J]. Journal of Sound and Vibration, 2013, 332(20): 4963-4978.

[2] 陳思雨,唐進元.間隙對含摩擦和時變剛度的齒輪系統動力學響應的影響[J].機械工程學報,2009,45(8): 119-124.

Chen Siyu, Tang Jinyuan. Effect of backlash on dynamics of spur gear system with friction and time-varying stiffness [J]. Chinese Journal of Mechanical Engineering, 2009, 45(8): 119-224. (in Chinese)

[3] 王三民,沈允文,董海軍.含摩擦和間隙直齒輪副的混沌與分叉研究[J].機械工程學報,2002,38(9):8-11.

Wang Sanmin, Shen Yunwen, Dong Haijun. Chaos and bifurcation analysis of a spur gear pair with combined friction and clearance[J]. Chinese Journal of Mechanical Engineering,2002,38(9):8-11.(in Chinese)

[4] 王彥剛,鄭海起,楊通強,等.非線性齒輪系統單齒故障動力學特性[J].振動、測試與診斷,2010,30(6):654-656.

Wang Yangang, Zheng Haiqi, Yang Tongqiang, et al. Nonlinear dynamic characteristics of gear system with single-tooth fault[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(6):654-656. (in Chinese)

[5] 李發家,朱如鵬,鮑和云,等.行星齒輪系動力學特性分析及試驗研究[J].南京航空航天大學學報, 2012, 44(4): 511-519.

Li Fajia, Zhu Rupeng, Bao Heyun, et al. Dynamics characteristic and experiment research on planetrary gear system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(4):511-519. (in Chinese)

[6] Al-shyyab A, Kahraman A. Non-linear dynamic analysis of a multi-mesh harmonic balance method: period-one motions [J]. Journal of Sound and Vibration, 2005, 284(1): 151-172.

[7] Al-shyyab A, Kahraman A. Non-linear dynamic analysis of a multi-mesh harmonic balance method: sub-harmonic motions[J]. Journal of Sound and Vibration, 2005, 284(2): 417-451.

[8] Ma Qinglong, Kahraman A. Period-one motions of a mechanical oscillator with periodically time-varying, piecewise-nonlinear stiffness [J]. Journal of Sound and Vibration, 2005, 284(4): 893-914.

[9] Lin Jian, Parker R G. Mesh stiffness variation instabilities in two-stage gear systems [J]. Journal of Vibration and Acoustics, 2002, 124(1):68-76.

[10]Liu Gang. Nonlinear dynamic of multi-mesh gear systems [D]. Kolumb City: The Ohio State University, 2007.

[11]Kim T C, Rook T E, Singh R. Effect of smoothing functions on the frequency response of an oscillator with clearance non-linearity [J]. Journal of Sound and Vibration, 2003, 263(3): 665-678.

[12]Cornell R W. Compliance and stress sensitivity of spur gear teeth [J]. Journal of Mechanical Design, 1981, 103(4): 447-452.

10.16450/j.cnki.issn.1004-6801.2015.03.011

*國家自然科學基金資助項目(51135003，U1234208)；長江學者和創新團隊發展計劃資助項目(IRT0816)；“高檔數控機床與基礎制造裝備”科技重大專項課題資助項目(2013ZX04011011)

2013-12-13；

2014-04-08

TH132.41

胡鵬，男，1986年7月生，博士研究生。主要研究方向為機械系統動力學與可靠性設計。曾發表《基于隨機攝動法的齒輪系統動態響應及靈敏度分析》(《東北大學學報》2014年第35卷第2期)等論文。

E-mail:penghu112800@163.com