鋼框架結構的地震損傷研究①

鄭山鎖， 代曠宇， 孫龍飛， 楊 威， 李文勇， 田 微

(1.西安建筑科技大學土木工程學院，陜西 西安 710055； 2.西安建筑科技大學建筑設計研究院，陜西 西安 710055)

鋼框架結構的地震損傷研究①

鄭山鎖1， 代曠宇1， 孫龍飛1， 楊 威1， 李文勇1， 田 微2

(1.西安建筑科技大學土木工程學院，陜西 西安 710055； 2.西安建筑科技大學建筑設計研究院，陜西 西安 710055)

基于預定損傷法對鋼框架構件主要設計參數進行損傷敏感度分析，研究主要設計參數與鋼框架結構梁、柱損傷的關系；揭示鋼框架結構梁、柱的損傷及梁、柱線剛度比、結構高寬比、柱軸壓比、銹蝕率對樓層損傷的影響規律；獲得樓層的損傷與整體結構損傷的關系，最終建立鋼框架結構的損傷演化模型。研究成果可為建立地震激勵下鋼框架結構的損傷模型提供理論基礎和數據支持。

鋼框架結構； 設計參數； 損傷敏感度； 損傷模型； 損傷表征

0 前言

建筑結構的倒塌破壞是造成地震災害的主要因素，因導致結構喪失其使用性和安全性引起巨大的人員傷亡和經濟損失。震害資料研究表明[1-2]，建筑結構往往因地震作用造成結構損傷，并且其損傷會隨地震動力荷載的增加而逐漸累積。建筑材料與結構的力學性能因其損傷累積而不斷退化，當建筑結構的損傷達到一定程度時，結構將無法繼續承受外部荷載，最終會發生整體或局部倒塌。

鋼結構因其質輕、高強、抗震性能好等諸多優點，被廣泛應用于大型商場、學校、工廠等建筑物中。目前關于鋼結構抗震性能和安全評估的研究得到了國內外的廣泛關注，但更多地集中于基于性能的設計方法對鋼結構進行抗震性能評估[3-4]，而針對鋼結構的地震損傷研究比較少。徐龍河等[1]提出了基于等效塑性應變和比能雙控的損傷模型，可以很好地評估強震下鋼結構豎向構件及層的損傷發展過程；楊清平等[3]采用彈塑性損傷模型對鋼結構在地震作用下的損傷進行了量化評估；文獻[5]建立了考慮結構地震反應滯回變形幅值對累積耗能損傷影響的雙參數損傷模型，并提出了基于易損性分析評估鋼結構在地震作用下損傷程度的方法。

本文基于理論計算與數值模擬，對鋼框架結構主要設計參數進行損傷敏感度分析，采用構件損傷-樓層損傷-結構損傷的研究思路，以期獲得鋼框架結構的損傷演化模型，從而更好地對結構進行抗震性能評估。

1 計算模型

工程采用鋼框架結構體系，平面尺寸24.0 m×19.2 m，跨度和柱距均為4.8 m，共5層，底層層高3.3 m，標準層層高均為3.0 m，結構平面布置見圖1。鋼框架梁的截面尺寸為H550 mm×300 mm×25 mm×30 mm，鋼框架柱的截面尺寸為H550 mm×450 mm×30 mm×45 mm，鋼材采用Q235B。樓面荷載為3.5 kN/m2，屋面荷載為2.0 kN/m2，恒荷載為8 kN/m2；地面粗糙類別為B類，基本風壓為0.35 kN/m2，基本雪壓為0.25 kN/m2。設計分組為一組；場地土類別為Ⅱ類；框架抗震等級為二級；抗震設防按Ⅷ度考慮；結構阻尼比取為0.05。

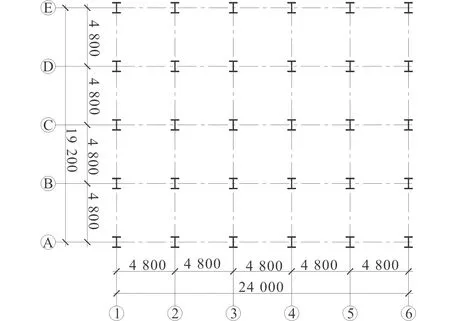
圖1 結構平面圖Fig.1 Structure plan

2 構件損傷研究

2.1 構件損傷的表征

2.1.1 鋼框架梁損傷表征

鋼框架梁是結構的主要受力構件之一，主要用于豎向荷載的承擔和整體結構魯棒性(Robustness)的維持。根據鋼框架梁的重要性和受力性能，本文選用損傷前后鋼框架梁的抗彎剛度作為指標來描述其損傷，如

(1)

式中，Db為鋼框架梁的損傷值；Bb，o和Bb，w分別為損傷前后構件的抗彎剛度值。

2.1.2 鋼框架柱損傷表征

構件的滯回耗能能力對于評價結構的抗震性能至關重要，良好的耗能能力，使構件可以吸收更多的地震能量，使結構免受地震破壞。鑒于鋼框架柱是結構的主要耗能構件，本文選用滯回耗能能力作為指標來描述鋼框架柱的損傷，如：

(2)

式中，Dc為鋼框架柱的損傷值；Eo和Ew分別為在循環荷載作用下損傷前后鋼框架柱的滯回耗能能力。

2.2 設計參數的損傷敏感度分析

為了對往復荷載作用下構件或結構損傷傳遞規律進行研究，采用文獻[6]提出的“預定損傷法”，通過對型鋼腹板高度、腹板厚度、翼緣寬度、翼緣厚度等參數進行損傷敏感度分析，得到影響構件損傷最為敏感的設計參數，為樓層損傷模型的建立提供理論基礎。

2.2.1 鋼框架梁損傷敏感度分析

調整型鋼截面，如腹板高度、腹板厚度、翼緣寬度、翼緣厚度來模擬鋼框架梁的初始損傷，得到各主要設計參數對型鋼梁損傷演化的影響規律(表1)。

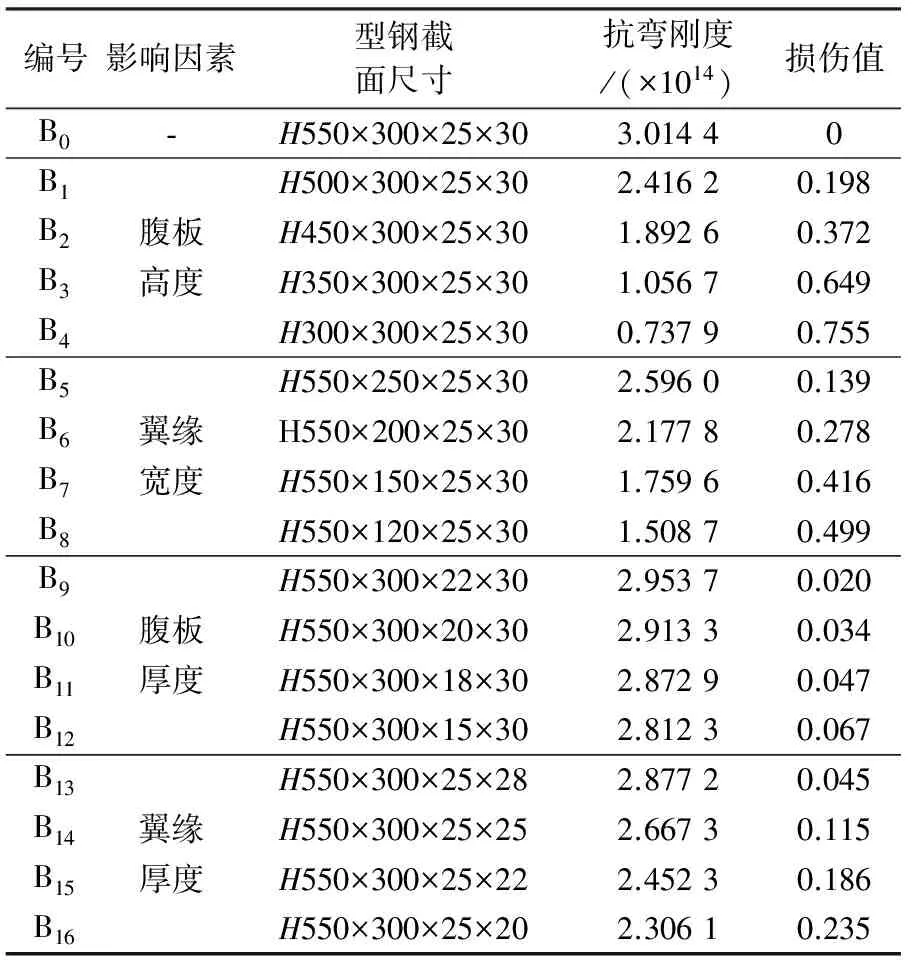
表1 各設計參數對鋼框架梁損傷的影響

注：(1)B0為原形結構構件；(2)表中基本單位為mm。

為消除量綱上的差異，引入各設計參數損傷前的原始值，得到鋼框架梁無量綱設計參數與損傷值之間的關系曲線(圖2)。由圖可知，腹板厚度及翼緣厚度的無量綱關系曲線基本呈線性；腹板高度及翼緣寬度的無量綱關系曲線相似，當損傷前后翼緣寬度比bo/b=2.5時，框架梁損傷值Db=0.499，關系曲線趨于平緩；隨損傷前后腹板高度比值的增大，框架梁的損傷變化速度最快，即鋼框架梁損傷對腹板高度最為敏感，翼緣寬度次之，腹板厚度最不敏感；綜合考慮，為實現初始預定損傷，優先調整鋼框架梁的腹板高度和翼緣寬度。

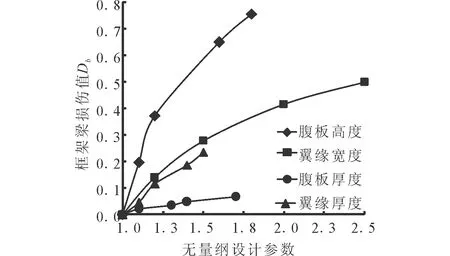
圖2 鋼框架梁的損傷關系曲線Fig.2 Damage curve of the steel frame beam

2.2.2 鋼框架柱損傷敏感度分析

通過調整柱的腹板高度、腹板厚度、翼緣寬度、翼緣厚度等設計參數來模擬鋼框架柱的初始損傷，并以損傷前后鋼框架柱滯回耗能能力的變化來描述損傷，對各影響因素進行損傷敏感度分析。各設計參數對鋼框架柱損傷的影響情況詳見表2。

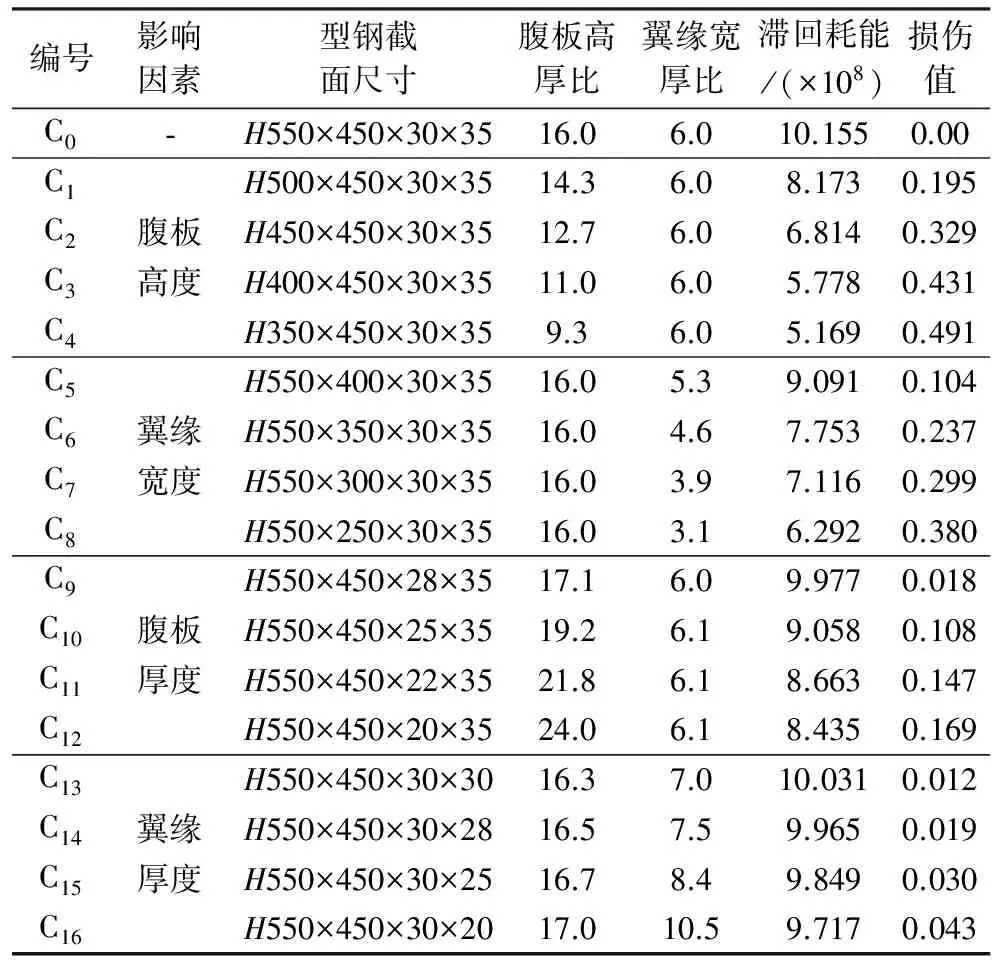
表2 各設計參數對鋼框架柱損傷的影響

注：(1)C0為原形結構構件；(2)表中基本單位為mm。

圖3為鋼框架柱無量綱設計參數與損傷值之間的關系曲線。由圖可知，當損傷前后翼緣厚度的比值to/t=1.75時，框架柱的損傷Dc=0.043，翼緣厚度的無量綱關系曲線基本呈線性關系；腹板高度、翼緣高度及腹板厚度的無量綱關系曲線基本相似，其中隨損傷前后腹板高度比值的增大，框架柱的損傷變化最快，即鋼框架柱損傷對腹板高度最為敏感，翼緣寬度次之，翼緣厚度最不敏感。綜合考慮，為實現初始預定損傷，優先調整鋼框架柱的腹板高度和翼緣寬度。

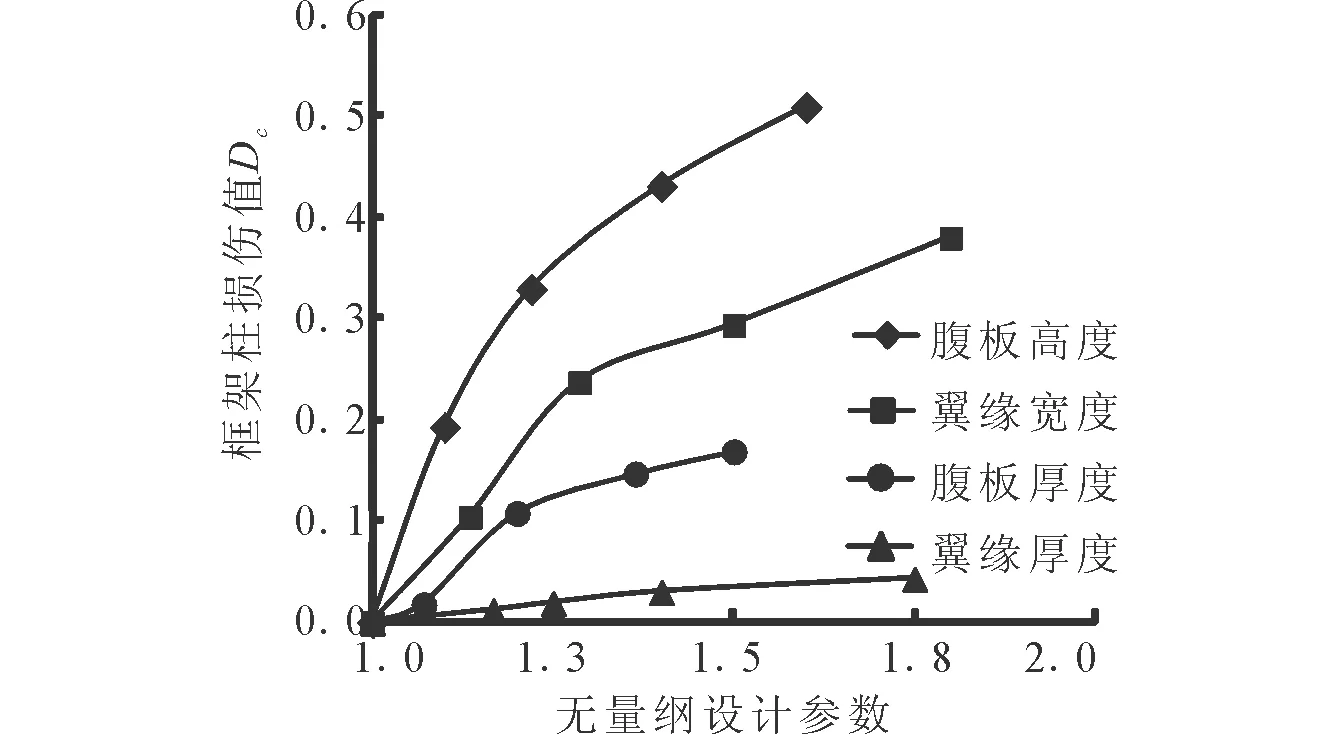
圖3 鋼框架柱的損傷關系曲線Fig.3 Damage curve of steel frame column

3 樓層損傷研究

3.1 樓層損傷的表征

本文鋼框架模型的整體變形是剪切型，可視樓層為整個鋼框架結構的一個單獨子結構，即其層間位移是相互獨立的，此時層間位移角由梁、柱及其節點的彈塑性變形構成。因此選取層間最大位移角作為往復荷載作用下的樓層損傷表征量。基于國內外相關研究成果，給出適用于鋼框架結構樓層損傷的表征函數：

(3)

式中，θmax，o為樓層損傷前的最大層間位移角；θmax，w為樓層損傷后的最大層間位移角。

3.2 鋼框架梁、柱損傷對樓層損傷的影響

3.2.1 初始損傷的實現

為明確鋼框架梁、柱損傷對其結構樓層損傷的影響，根據構件主要設計參數的損傷敏感度分析結果，通過調整型鋼的腹板高度及翼緣寬度等設計參數來對鋼框架梁、柱的初始損傷進行數值模擬。其中，損傷評估標準采用文獻[7]確定的鋼框架結構在不同損傷程度下的震害指數范圍。經反復調試，確定鋼框架梁、柱在發生輕度、中度、及重度損傷時型鋼的截面尺寸情況，見表3。

3.2.2 樓層損傷分析

采用ABAQUS軟件對鋼框架結構樓層在往復荷載作用下的動力響應進行模擬分析，揭示一類和多類構件在發生不同程度的損傷時對結構樓層損傷的影響規律，分析結果見表4。

圖4為單類與多類構件損傷與樓層損傷的關系曲線圖。由圖可知，梁、柱構件發生相同損傷時，框架柱的損傷對樓層損傷的影響比框架梁更為顯著；與單類構件相比，梁、柱同時發生損傷時樓層的損傷更加突出。

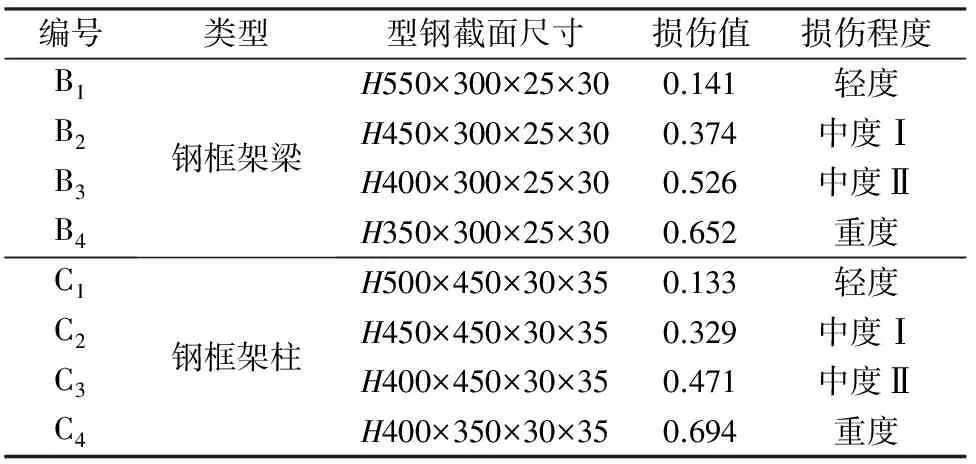
表3 鋼框架構件設計參數

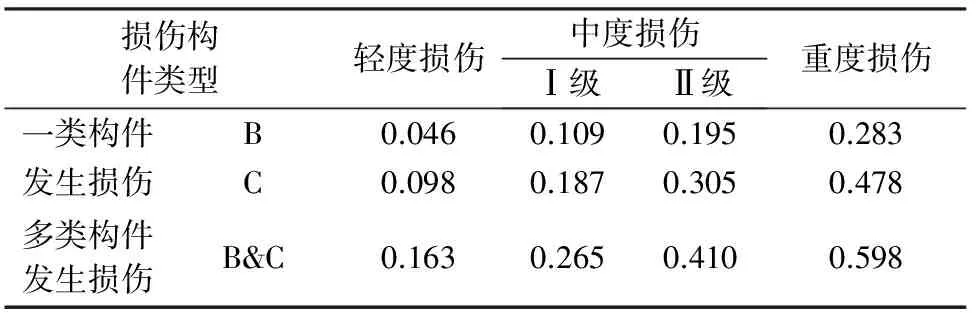
表4 不同程度損傷對樓層損傷的影響

注：(1)一類構件發生損傷指的是樓層中一類構件(梁或柱)發生相同程度的損傷(輕度、中度及重度)，多類構件發生損傷指的是樓層中兩類構件同時發生相同程度的損傷；(2)B代表鋼框架梁，C代表鋼框架柱，B&C代表鋼框架梁、柱。

圖4 構件損傷與樓層損傷的關系曲線Fig.4 The relationship between member damage and storey damag

采用Origin軟件對以上分析結果進行回歸分析表明：梁、柱損傷與樓層損傷之間基本呈指數關系，諸類構件損傷與結構樓層損傷之間的關系函數表達式為：

(4)

(5)

式中，Ds為樓層損傷值；Db、Dc分別為框架梁、柱的損傷值。

3.3 其他因素對樓層損傷的影響

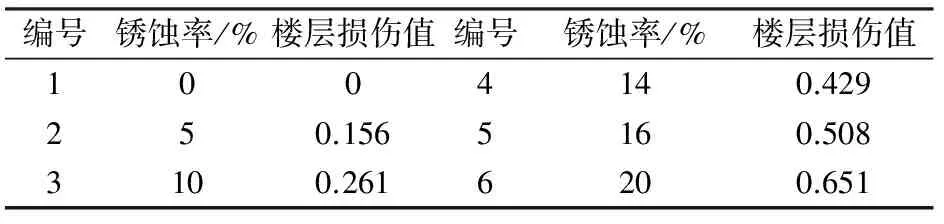
考慮到梁柱線剛度比、結構高寬比、柱軸壓比、構件銹蝕率等對框架結構樓層損傷亦有影響。本文研究了各因素對樓層損傷的影響，見表5～表8。

建立各因素與樓層損傷的關系曲線，如圖5所示，并分別得到各敏感因素與樓層損傷的函數關系式：

(6)

(7)

(8)

當ηs≤10%時

(9)

當ηs>10%時

(10)

式中，Ds為樓層損傷值；s、ζ、λ、ηs分別為梁柱線剛度比、結構高寬比、柱軸壓比和構件截面銹蝕率。

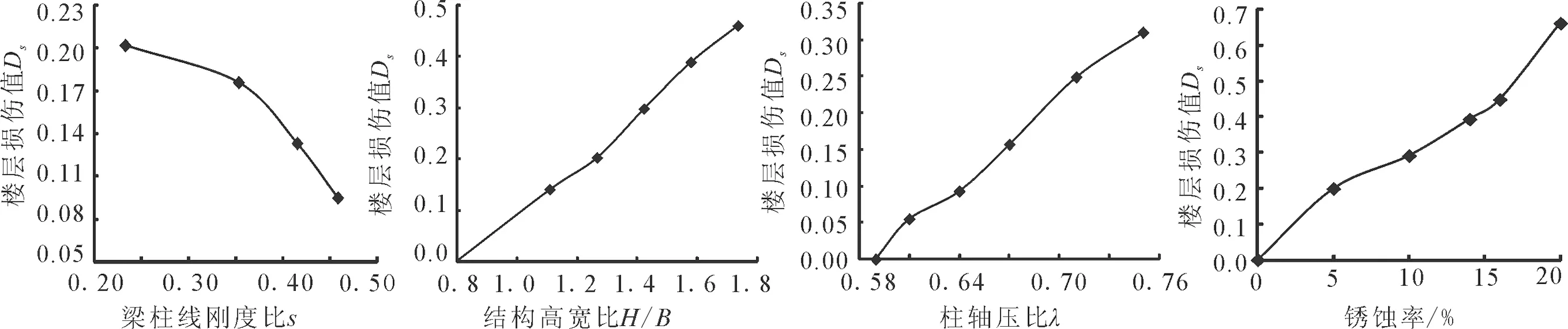
圖5 敏感因素與樓層損傷的關系曲線Fig.5 The relationship between sensitive factors and storey damage

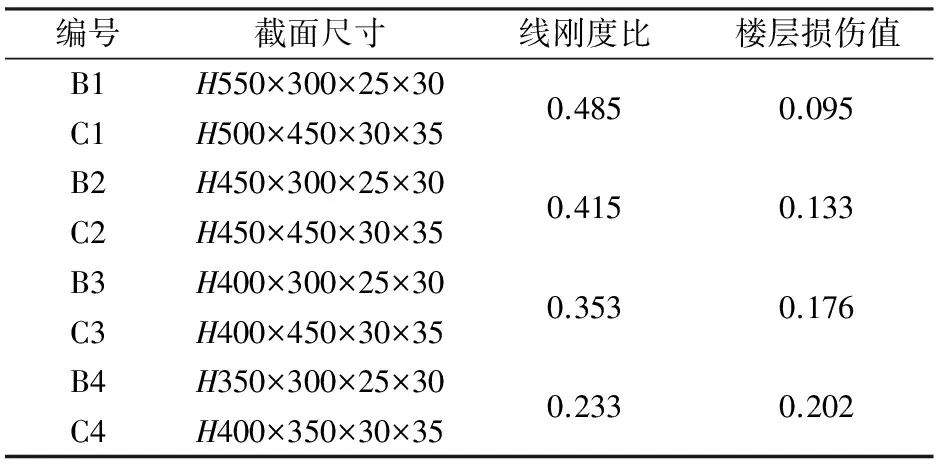
表5 梁柱線剛度比對樓層損傷的影響

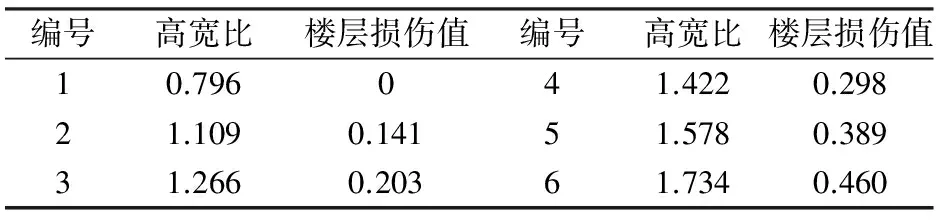
表6 結構高寬比對樓層損傷的影響

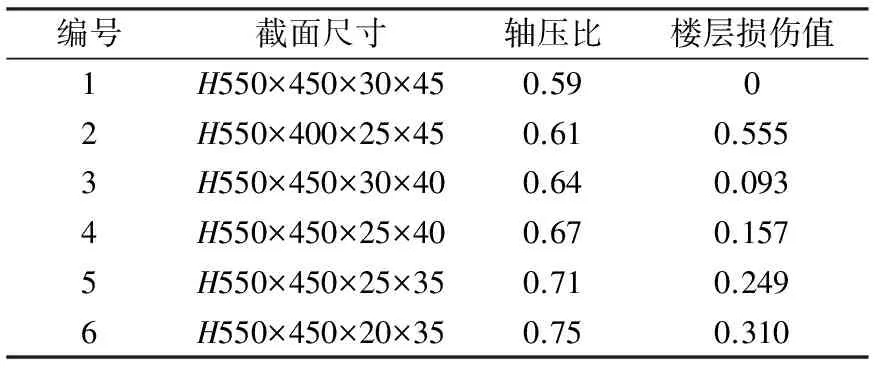
表7 柱軸壓比對樓層損傷的影響

3.4 適用于鋼框架結構樓層的損傷模型

鑒于國內外對結構地震損傷模型的研究[8]，建立鋼框架結構樓層地震損傷模型，模型由梁、柱構件損傷程度和設計參數兩部分組成：

(11)

式中，f2(Db，Dc)反映構件的損傷程度對樓層損傷的影響，鋼框架梁、柱損傷程度與結構樓層損傷之間的關系見式(4)、(5)；f1(s，ζ，λ，ηs)綜合反映其他設計參數對樓層損傷的影響，可表達為：

(12)

式中，a、b、c、d、g均為待定系數，可由上述分析結果回歸得到：

(13)

4 結構整體損傷研究

4.1 結構整體損傷表征量

文獻[6]研究指出，各樓層損傷值之和不等于整體結構的損傷值，主要原因是結構底部樓層的損傷對整體結構的損傷影響相對突出，且隨樓層位置的提高而衰減。鑒于此，本文引入結構樓層滯回耗能的層間參與系數以反映各樓層在整個結構滯回耗能中的貢獻。樓層滯回耗能參與系數定義為

(14)

式中，EH，i為第i個樓層的滯回耗能；EH為整體結構的總耗能，EH=∑EH，i，∑φi=1。基于廣義力做功理論，采用力矩M與轉角θ的乘積表示諸樓層的滯回耗能，表達式為：

(15)

式中，MH，i為樓層第i列柱端的彎矩；θi為第i個樓層的層間位移轉角，其中柱端彎矩與樓層層間位移角均通過軟件ETABS求得，因此結構損傷表征量可表達為：

(16)

式中，DH為結構損傷值；Ds，i為第i個樓層的損傷值，Ds，i=1-EH，i，w/EH，i，o，EH，i，o和EH，i，w分別為損傷前后樓層的滯回耗能。

4.2 樓層損傷對結構損傷的影響

4.2.1 初始損傷的實現

為研究地震作用下樓層損傷對結構損傷的影響，基于上述研究成果，預先賦予指定樓層初始損傷，研究損傷樓層數量、位置及損傷程度對結構損傷的影響。經反復調試，確定樓層在發生不同程度損傷時對應的構件情況，見表9。

表9 樓層設計參數

4.2.2 結構整體損傷分析

為研究樓層損傷位置及程度對鋼框架結構地震損傷的影響規律，研究鋼框架結構在El-Centro地震波激勵下單個樓層損傷對結構動力特性的影響，揭示樓層損傷對結構損傷的影響規律，見表10。

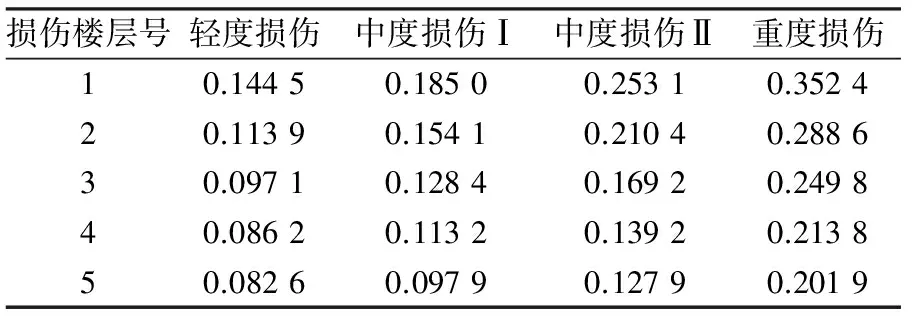
表10 樓層發生不同程度損傷時整體結構的損傷值

圖6(a)給出了損傷樓層位置及程度與結構損傷的關系曲線。由圖可知，當樓層發生相同程度的損傷時，底層對結構損傷的影響最為突出。將圖6(a)的四條關系曲線繪制于同一平面，并分別進行回歸處理，得到樓層在不同程度損傷時樓層位置與結構損傷間的擬合曲線，如圖6(b)所示。

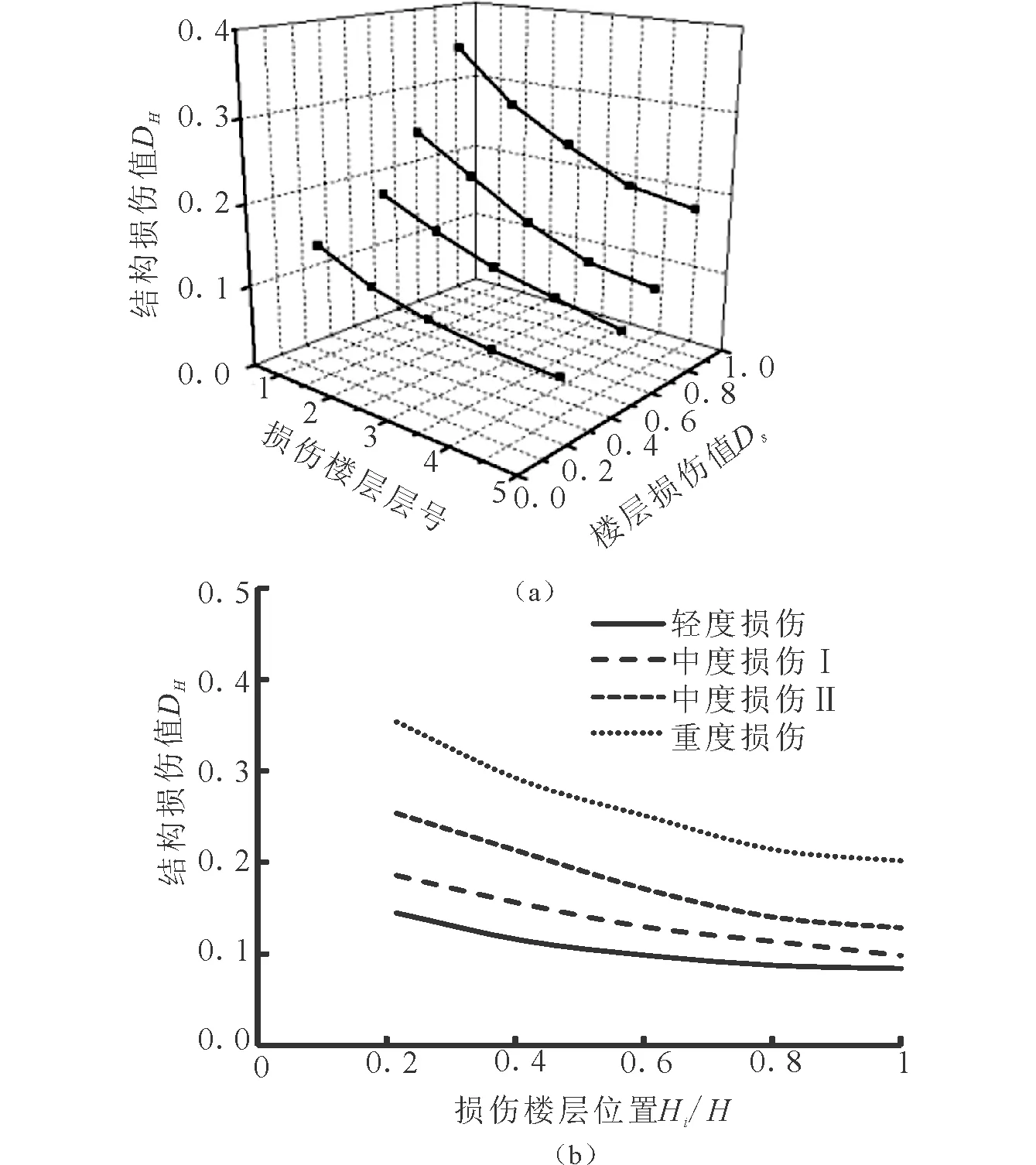
圖6 樓層損傷與結構損傷的關系曲線Fig.6 The relationship between storey damage and overall structure damage

曲線回歸分別獲得樓層輕度損傷、中度損傷I、中度損傷II及重度損傷時樓層的位置與結構損傷間的數學表達式：

(17)

(18)

(19)

(20)

將式(18)和(19)合并為：

(21)

進一步對其四條擬合曲線進行回歸處理，獲得單個樓層損傷時損傷位置及程度與結構損傷值間的關系式：

(22)

式中，DH，i為第i個樓層損傷時結構的損傷值；Ds，i為第i個樓層的損傷值；Hi為損傷樓層距地面的高度；H為結構總高度，Hi/H反映的是損傷樓層的位置。

鑒于樓層發生中度損傷時Hi/H與整體結構損傷的關系曲線具有一定的普遍性，本文以中度損傷為例建立結構地震損傷模型，首先引入樓層損傷權值系數：

(23)

式中，DH，i為樓層發生中度損傷時第i個樓層損傷所引起的結構損傷量。結合式(21)～(23)獲得多個樓層發生不同程度損傷時，整體結構地震損傷量的計算公式：

(24)

4.3 地震波特性對結構地震損傷的影響

為研究地震波峰值速度與峰值加速度比值Ψ對框架結構損傷破壞的影響，在對鋼框架結構進行彈塑性地震反應分析時，向結構分別輸入16條地震波，具體參數見表11。分析16條地震波作用下結構的動力響應，計算出整體結構的地震損傷值，獲得地震波峰值速度與峰值加速度比值對框架結構損傷破壞的影響。為更直觀地研究地震波峰值速度與峰值加速度之比對結構地震損傷的影響規律，將結果進行擬合分析，如圖7所示。

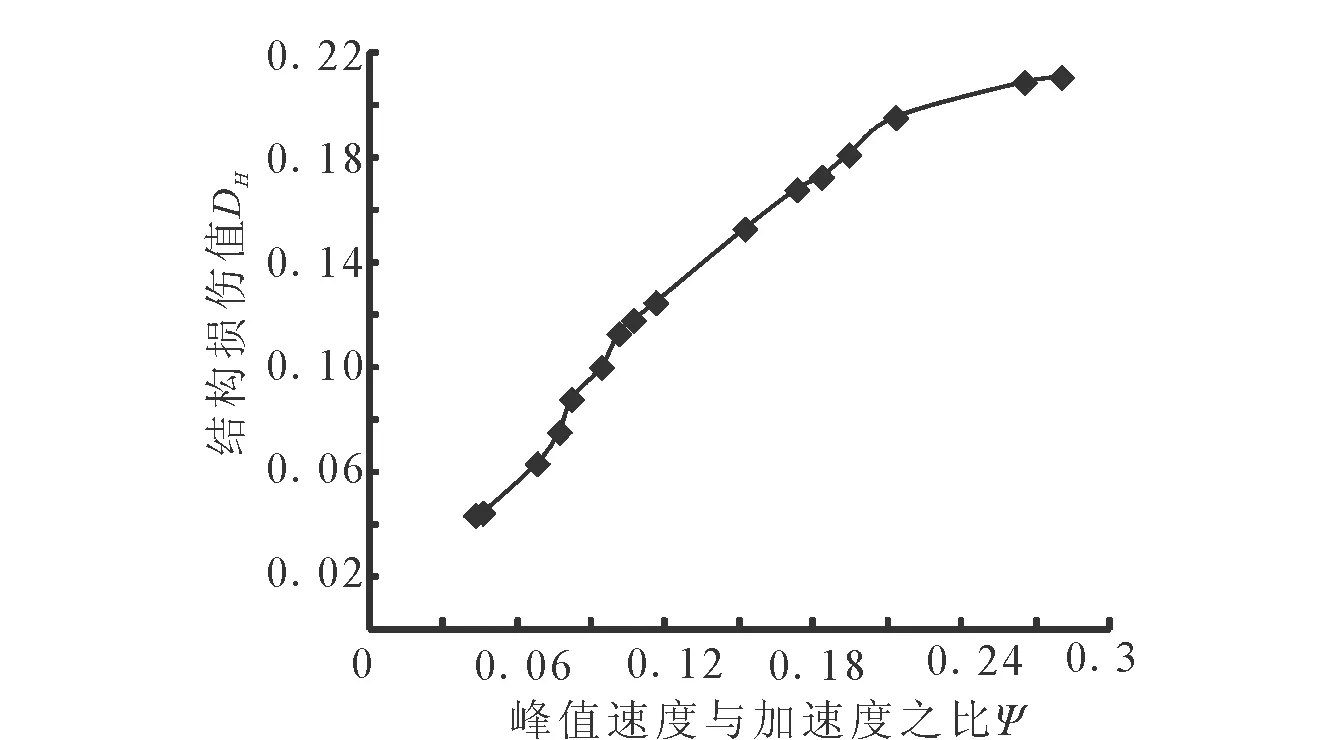
圖7 Ψ值與整體結構地震損傷值之間的關系曲線Fig.7 The relationship between value Ψ and seismic damage value of overall structure

對結果進行回歸分析，建立D與Ψ之間的數學關系式：

(25)

式中，D為整體結構損傷值；Ψ為地震波峰值速度與峰值加速度比值。

4.4 適用于鋼框架結構的地震損傷模型

鑒于國內外關于結構地震損傷模型的研究成果[9-10]，建立整體結構地震損傷模型，該模型由地震波屬性和損傷發生的位置及程度兩部分組成：

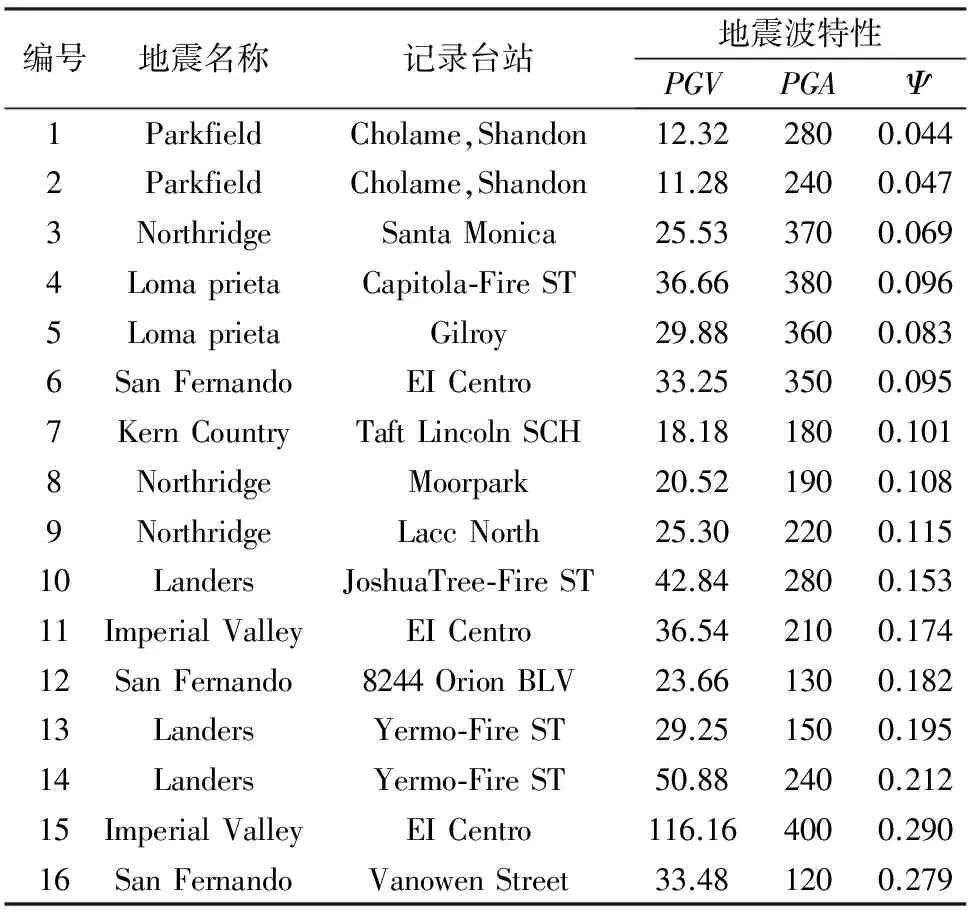
表11 地震波特性一覽表

(26)

式中，f1(Ψ)為地震波屬性對整體結構損傷的影響函數，函數表達式設定為式(27)；f2(Hi/H，Ds，i)為損傷發生的位置Hi/H及程度Ds，i與整體結構損傷之間的關系函數，見式(24)。

(27)

式中，a、b為待定系數，由分析結果回歸得到：

(28)

5 結論

以4跨5層鋼框架結構為研究對象，基于理論計算與數值模擬，研究了構件損傷對樓層損傷的影響以及樓層損傷對整體結構損傷的影響，得出以下結論：

(1) 通過設計參數的損傷敏感度分析，可知型鋼腹板高度和翼緣寬度對構件損傷影響最大，為實現構件的初始損傷，可優先考慮調整腹板高度和翼緣寬度。

(2) 基于構件損傷，對樓層的損傷敏感性進行分析。結果表明：梁、柱構件發生相同損傷時，框架柱的損傷對樓層損傷的影響更為顯著；與單類構件損傷相比，梁、柱同時發生損傷時樓層的損傷更加嚴重。

(3) 本文所建立的結構地震損傷演化模型考慮了結構設計參數和其他影響因素，具有較高的適用性，可為鋼框架結構的倒塌評估提供理論支持。

)

[1] 徐龍河，楊冬玲，李忠獻.基于應變和比能雙控的鋼結構損傷模型[J].振動與沖擊，2011，30(7)：218-222.XULong-He，YANGDong-ling，LIZhong-xian.StrainandEnergyRatio-basedDamageModelofaSteelStructure[J].JouranalofVibrationandShock，2011，30(7)：218-222.(inChinese)

[2] 鄭山鎖，田進，韓言召，等.考慮銹蝕的鋼結構地震易損性分析[J].地震工程學報，2014，36(1)：1-6.ZHENG Shan-suo，TIAN Jin，HAN Yan-zhao，et al.Steel Structure Seismic Vulnerability Analysis Considering Steel Corrosion[J].China Earthquake Engineering Journal，2014，36(1)：1-6.(in Chinese)

[3] 楊清平，袁旭東，孫麗.基于塑性變形的鋼結構地震損傷量化[J].沈陽建筑大學學報，2011，27(5)：886-890.YANG Qing-ping，YUAN Xu-Dong，SUN Li.The Steel Structure Seismic Damage Quantitative Research Based on Plastic Deformation[J].Journal of Shenyang Jianzhu University：Natural Science)，2011，27(5)：886-890.(in Chinese)

[4] Federal Emergency Management Agency.FEMA273.Guidelines for Seismic Rehabilitation of Buildings[S].Washington，DC：1997.

[5] 徐龍河，單旭，李忠獻.強震下鋼框架結構易損性分析及優化設計[J].工程力學，2013，30(1)：175-179.XU Long-he，SHAN Xu，LI Zhong-xian.Vulnerability Analysis and Optimization Design for Steel Frame Structure Under Strong Earthquakes[J].Engineering Mechanics，2013，30(1)：175-179.(in Chinese)

[6] 陶清林.地震激勵下SRC框架-RC核心筒混合結構損傷模型研究[D].西安：西安建筑科技大學，2011 TAO Qing-lin.Research on the Damage Model of SRC Frame-RC Core Wall Hybrid Structure under Seismic Excitation[D].Xi’an University of Architecture and Technology，2011.(in Chinese)

[7] 歐進萍，牛荻濤，王光遠.多層非線性抗震鋼結構的模糊動力可靠分析與設計[J].地震工程與工程振動，1990，10(4)：27-37.OU Jin-ping，NIU Di-tao，WANG Guang-yuan.Fuzzy Dynamical Reliability Analysis and Design of Multi-storey Nonlinear Aseismic Steel Structures[J].Journal of Earthquake Engineering and Engineering Vibration，1990，10(4)：27-37.(in Chinese)

[8] Young-Ji Park，Alfredo H-S Ang，Yi Kwen Wen.Seismic Damage Analysis of Reinforced Concrete Buildings[J].Journal of Structural Engineering，ASCE，1985，111(4)：740-757.

[9] David V Rosowsky，Bruce R.Performance-Based Engineering of Wood Frame Housing：Fragility Analysis Methodology[J].Journal of Structural Engineering，2002，128(1)：32-38.

[10] Sivia L Dimova，Anaxagoras Elenas.Seismic Intensity Parameters for Fragility Analysis of Structures with Energy Dissipating Devices[J].Structural Safety，2002(24)：1-28.

Research on the Seismic Damage of Steel Frame Structure

ZHENG Shan-suo1， DAI Kuang-yu1， SUN Long-fei1， YANG Wei1， LI Wen-yong1，TIAN Wei2

(1.SchoolofCivilEngineering，Xi’anUniversityofArchitectureandTechnology，Xi’an，Shaanxi710055，China；2.ArchitecturalDesignandResearchInstitute，Xi’anUniversityofArchitectureandTechnology，Xi’an，Shaanxi710055，China)

Because of their light weight，high strength，and good seismic performance，steel structures are widely used in construction.At present，the research on the seismic performance and safety assessment of steel structures receives widespread attention at home and abroad；most of this research focuses on assessing the seismic performance of steel structures based on the performance design method，with little research on earthquake damage.Under such circumstances，the author firstly analyzed the main design parameters，such as web height，web thickness，flange width，and flange thickness，which affect the component damage evolution rule，and the author found that the most sensitive design parameters are web height and flange width，which provided a theoretical basis for the establishment of the storey damage model.Then，according to the analysis results，we obtained the damage value relationship between the frame beam，frame column，and storey damage evolution and analyzed the effect of sensitive factors on storey damage evolution，such as the stiffness ratio of column to beam，the height-width ratio of the structure，the axial-compression ratio of the frame column，and the steel corrosion rate.Finally，in order to study the influence of storey damage location and degree to the seismic damage of the steel frame structure，the author revealed the influence of storey damage on structural damage by analyzing the effect of single-storey steel frame structure damage on structural dynamic characteristics under El Centro seismic wave excitation.Inputting multiple seismic waves，the author got the relation between the damage value of structural integrity and the velocity-to-acceleration ratio of the seismic wave peak and ultimately established the damage evolution model of steel frame structures.The multi-level damage evolution model of “component-storey-structure” can provide the theoretical foundation and basic data support for establishing the storey damage model of steel frame structures under seismic excitation.

steel frame structure； design parameter； damage sensitivity； damage model； damage characterization

2014-06-11

國家科技支撐計劃(2013BAJ08B03)；國家自然科學基金(50978218，51108376)；高等學校博士學科點專項科研基金(20136120110003)；陜西省科研項目(2012K12-03-01，2011KTCQ03-05，2013JC16)

鄭山鎖(1960-)，男，陜西人，博士生導師，從事結構工程抗震研究.

TU528.01

A

1000-0844(2015)02-0290-08

10.3969/j.issn.1000-0844.2015.02.0290