實對稱矩陣應用的兩點體現

孫衛衛

（青島理工大學琴島學院，山東 青島 266106）

0 引 言

通過利用實對稱矩陣的一些特性可以有效地解決一般的二次曲面［1－3］方程圖形的推斷與二元以上多元函數極值［1－3］的求解問題。現在就從上述兩個角度來闡述實對稱矩陣的具體應用。

1 一般的二次曲面方程的圖形推斷

對于一些簡單的二次曲面方程很容易推斷其形狀，而對于復雜的二次曲面方程推斷其形狀是比較困難的，例如z＝xy。而實對稱矩陣［4－5］的加入，使得這個問題的解決變的容易許多，以下給出實對稱矩陣對一般的二次曲面方程圖形推斷的具體方法。

二次曲面的一般方程［6］

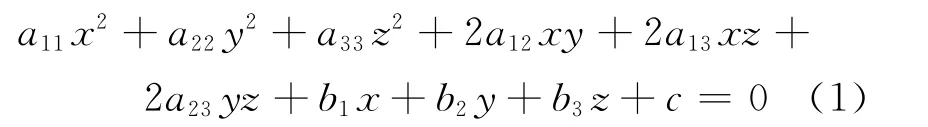
其中，aij，bi，c為實數（i，j＝1，2，3）。

設：

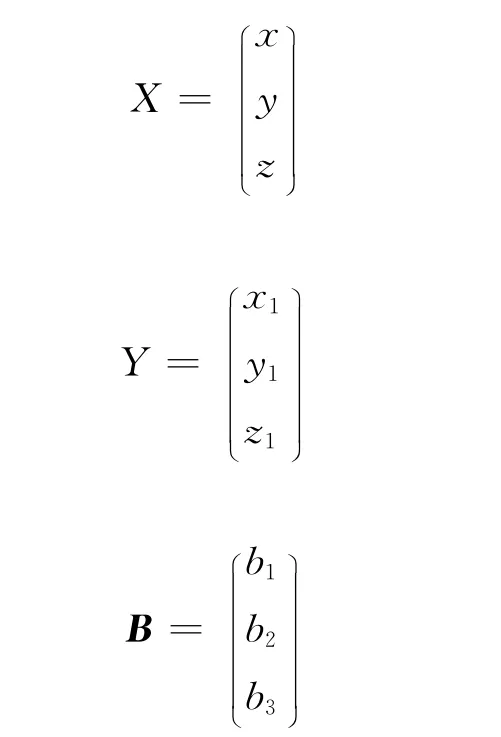
二次曲面可表示為：

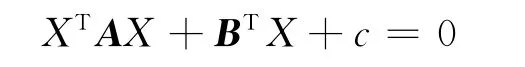
由于A為實對稱矩陣，因此存在正交的矩陣P，有：

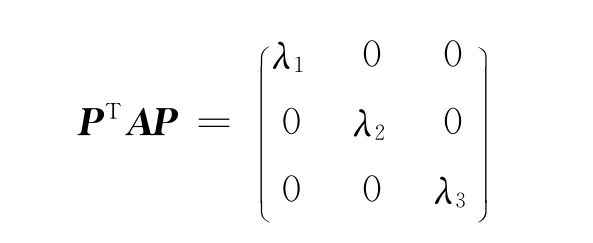
其中，λ1，λ2，λ3為特征值。

由正交變換X＝PY可得：

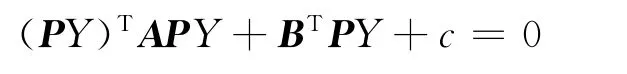
令（d1，d2，d3）＝BTP，整理得：

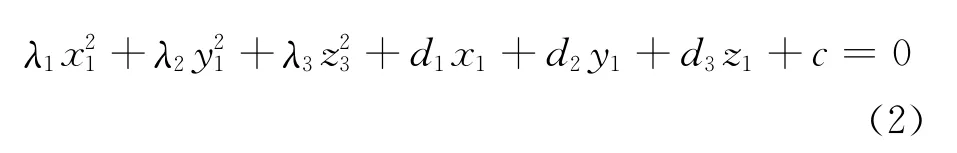
又因為正交變換具有保持向量內積和長度不變的性質［4－5］，因此可得如下定理：

定理1 方程（1）所表示的曲面形狀與方程（2）所表示的曲面形狀相同。

定理1正是運用了實對稱矩陣在正交矩陣的作用下可以對角化的性質而得到的，所以，如果遇到非標準形式下的二次曲面方程，也可以通過這一性質將其化簡，從而推斷其圖形。下面通過具體例題來實現實對稱矩陣的具體運用。

例1：推斷下列方程表示怎樣的圖形：

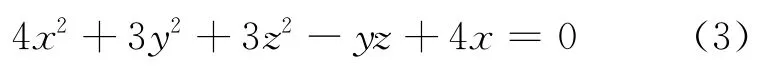
解：得實對稱矩陣：

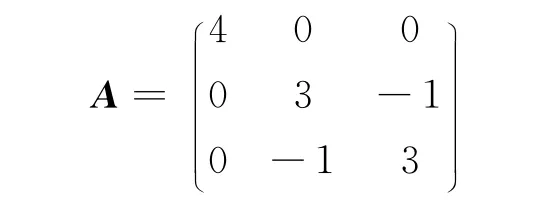
存在：

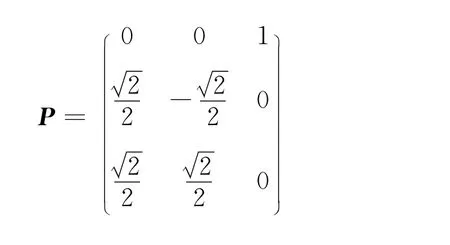
有：

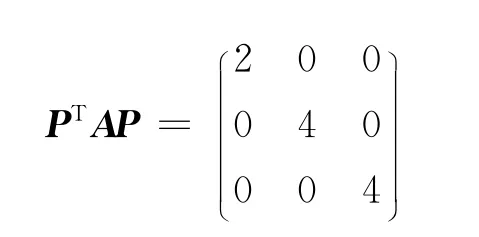
又：

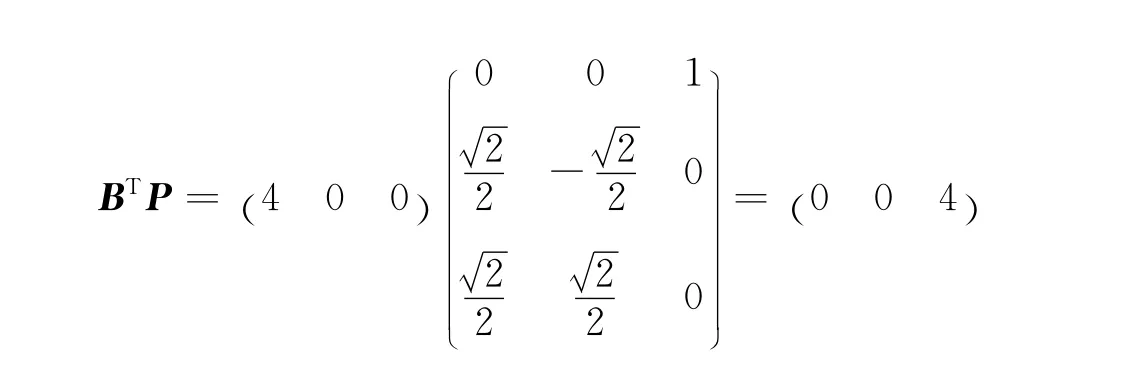
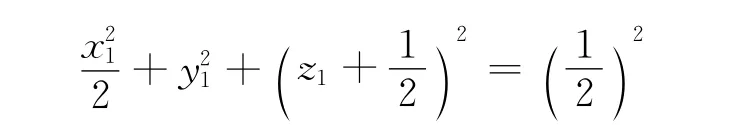
因此式（3）表示橢球面。

2 多元函數極值的求法

二元函數z＝f（x，y）在（x0，y0）的某鄰域內連續且具有一階、二階連續的偏導數，又

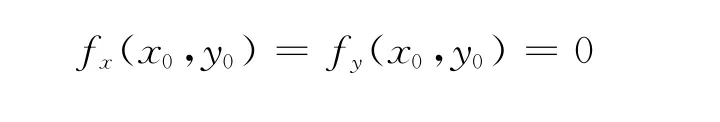
令

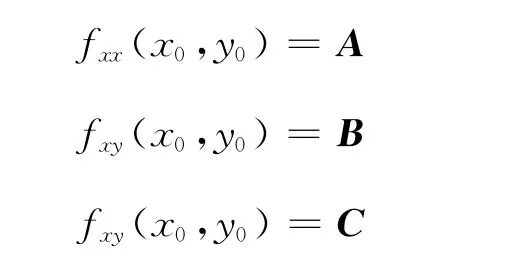
則有：

1）AC－B2＞0，（x0，y0）是極值點，A＞0是極小值點，A＜0是極大值點；

2）AC－B2＜0，（x0，y0）不是極值點；

3）AC－B2＝0，無法判定。

設矩陣

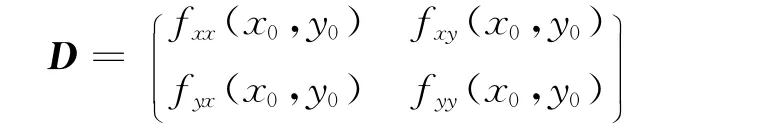
又

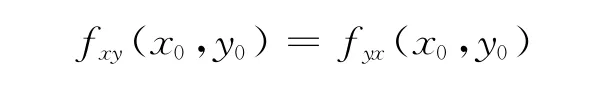
1）D正定，（x0，y0）是極小值點；

2）D負定，（x0，y0）是極大值點；

3）D不定，（x0，y0）不是極值點（這一結論也可由泰勒公式進行證明，詳見文獻［2－3］）。

將這一結論進行推廣：

設：u＝f（P）＝f（x1，x2，…，xn），u＝f（x1，x2，…，xn）在P0（x10，x20，…，xn0）某鄰域內連續，并具有一階、二階連續的偏導數，又有，由于，2，…，n），因此引入實對稱矩陣：

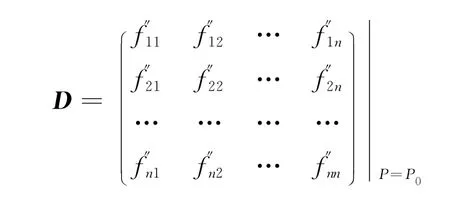
則有結論2：

1）D正定，（x0，y0）是極小值點；

2）D負定，（x0，y0）是極大值點；

3）D不定，（x0，y0）不是極值點（這一結論也可由多元函數的泰勒公式進行證明，詳見文獻［7］）。

將結論2運用到三元函數，并根據實對稱矩陣的正定性與順序主子式的關系可得如下定理：

定理2 三元函數u＝f（x，y，z）在（x0，y0，z0）的某鄰域內連續并具有一階、二階連續的偏導數，且fx（x0，y0）＝fy（x0，y0）＝fz（x0，y0）＝0，又二階混合偏導相等，引入實對稱矩陣：

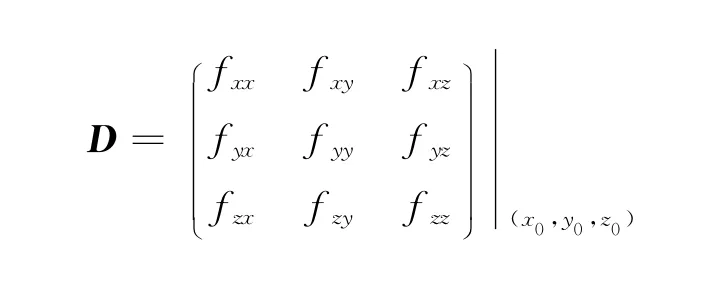
則有如下結論：

1）｜D｜＞0

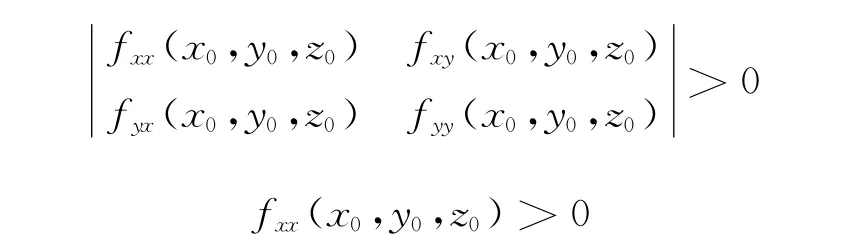
（x0，y0，z0）為極小值點；

2）｜D｜＜0

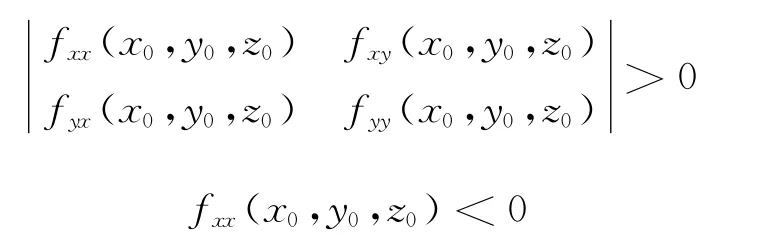
（x0，y0，z0）為極大值點；

3）｜D｜＝0，無法判定；

4）不屬于上述3種情況，則不是極值點。

定理2正是運用了實對稱矩陣的正定性的判別方法而得到的，所以，如果三元函數的極值點的判定都可以根據｜D｜的順序主子式來進行準確的分析。

下面通過具體例題來實現這一具體應用。

例2：求f（x，y，z）＝e2x（x＋y2＋2y）＋z3－3z極值。

解：求一階偏導得：

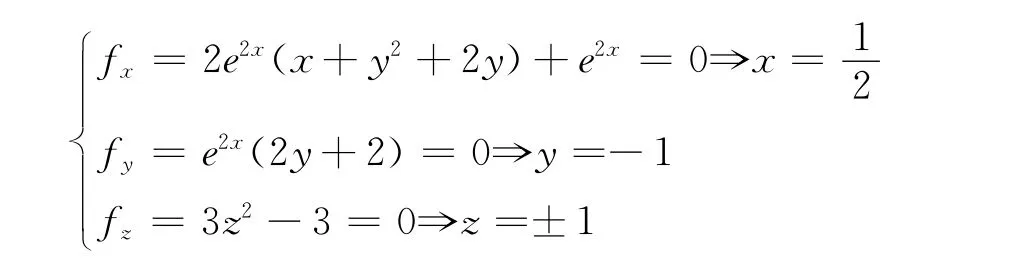
又

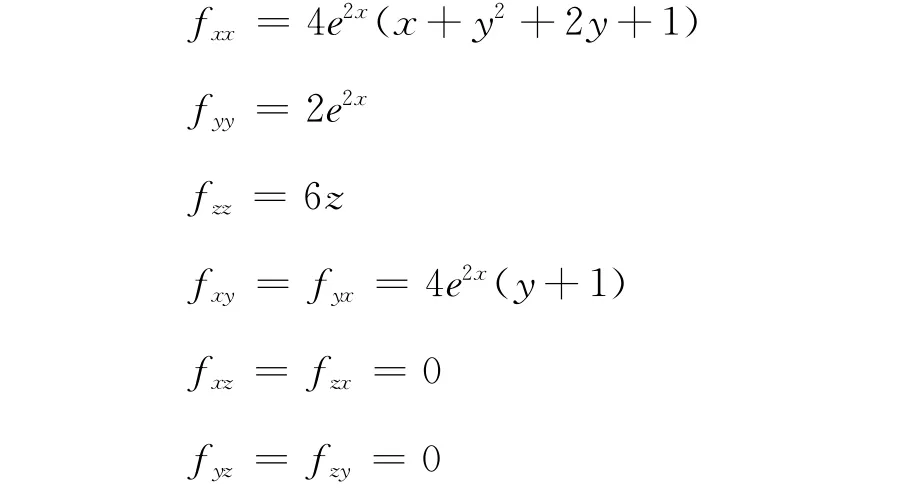
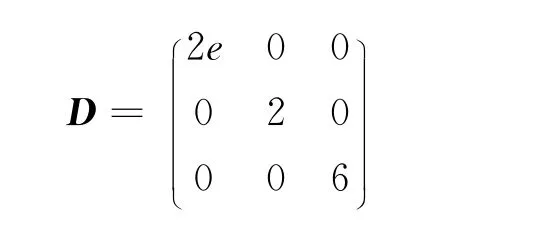
由定理2知，它是極小值點。

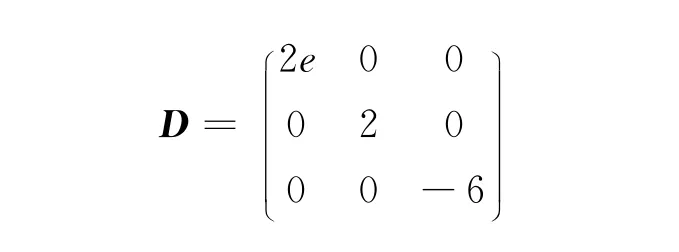
由定理2知，它不是極值點。

通過以上兩方面應用，將實對稱矩陣抽象的特性進行了運用，更加體現了它的實用價值。

［1］ 同濟大學數學系.高等數學（下冊）［M］.6版.北京：高等教育出版社，2007.

［2］ 華東師范大學數學系.數學分析（下冊）［M］.4版.北京：高等教育出版社，2010.

［3］ 徐森林.數學分析（第三冊）［M］.北京：清華大學出版社，2007.

［4］ 吳贛昌.線性代數（理工類）［M］.4版.北京：中國人民大學出版社，2011.

［5］ 黃益生.高等代數［M］.北京：清華大學出版社，2014.

［6］ 楊文茂.空間解析幾何［M］.武漢：武漢大學出版社，2004.

［7］ 紀躍芝.用矩陣的正定性判定多元函數的極值［J］.吉林工學院學報，1995，16（4）：71－75.