二階中立型多時滯差分方程的振動性和漸近性

鄭允利

（徐州生物工程職業技術學院 基礎部，江蘇 徐州 221006）

1 引言

由于計算機科學、生物數學、現代物理等自然科學與邊緣科學的迅速發展，對時滯差分方程定性理論的研究近年來十分活躍.許多學者對二階中立型時滯差分方程的振動性、漸近性及正解存在性作了探討，取得了大量成果[1-7].但已有文獻中所研究的方程大都是單時滯的，而從實際中抽取出來的數學模型通常是多時滯的.任榮霞、吳淑慧在文獻[1]中研究了二階不穩定中立型非線性差分方程

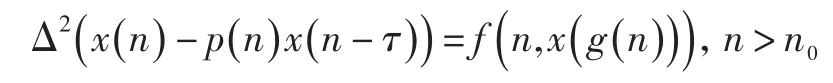
得到在p(n)的不同條件下及當g(n)＜n時，該方程有界解振動的若干充分條件；邢海龍等在文獻[5]中討論了二階中立型非線性多時滯差分方程n>n0.建立了該方程分別在和的條件下，每個有界解振動的充分條件.

在此基礎上，下面將研究一類二階中立型多時滯差分方程

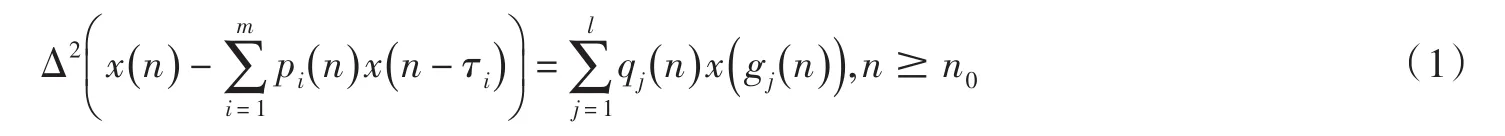
的振動性和漸近性，其中{ pi(n ) } 是非負實數序列，τi，i=1,2,...,m是非負整數，且存在非負整數τ，使得τ=max{τi, i=1,2,...,m} ； {qj( n ) } 為非負實數序列，gj:N0→N0，且j=1,2,...,l.令

2 預備知識

“ Δ”表示向前差分算子，即 Δ x(n)=x(n + 1)-x(n)；Z表示所有整數構成的集合，設 a ∈Z，記N(a)={a , a+1,…},N=N(0).

一個差分方程的解{x ( n ) } 稱為最終為正的，是指存在正整數M，使得n∈N(M ) 時，有 x (n)>0；若存在正整數M，使得n∈N(M ) 時，有 x (n ) ＜0，則稱{x ( n ) } 最終為負的.

一個差分方程的解{x ( n ) } 振動，是指{x ( n ) } 既不最終為正，也不最終為負；否則，稱之為非振動的.一個差分方程稱為振動的，如果方程的所有解都是振動的.

引理2.1[7]假定i=1,2,…,m,且，若其中 | L |＜∞，則存在，且等于

3 主要結果

定理3.1假定g()n＜n,n≥n0，且下列條件成立

（H1）存在 p ∈[0 , 1) 使得；（H2）則方程（1）所有有界解振動.

證明設 x(n ) 是方程（1）的最終有界正解，則存在n1≥n0，當n≥n1時，有 x (n - τ)>0，x(gj( n ) ) >0.由方程（1）和（2）式得，當 n >n1時，有 Δ2z(n)>0，因此 Δ z(n)最終定號.如果 Δz(n)>0，則必有nl i→m∞z(n)=∞ ，這與z(n)有界矛盾，故Δz(n)≤0.從而z(n)嚴格單調下降，因而z(n)只能最終為正或最終為負.

若z(n ) 最終為負，即存在n2>n1，當n≥n2時，有 z (n ) ＜0.記1≤mia≤xm{x ( n - τi)}=x(n - τ)，由（2）式和（H1）可知當 n ≥n2+kτ 時，有 x (n)＜px(n - τ ) ＜pkx(n - kτ).由上式可得nl i→m∞x(n)=0，從而nl i→m∞z(n)=0，這與Δz(n)≤0且z(n)＜0矛盾.

若z(n)最終為正，根據z(n ) 的性質，存在n2>n1，當n≥n2時

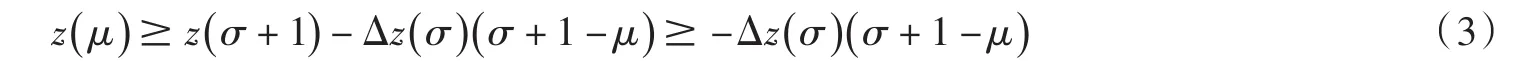
令 σ=g(n),μ=g(s) ，根據（3）式和方程（1）得

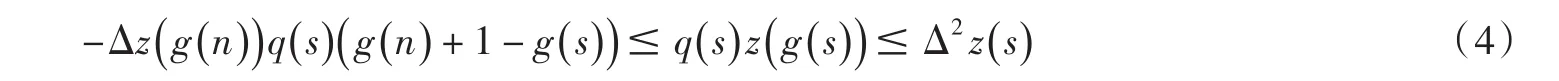
將（4）式兩端關于 s 從 g (n)到n-1求和得

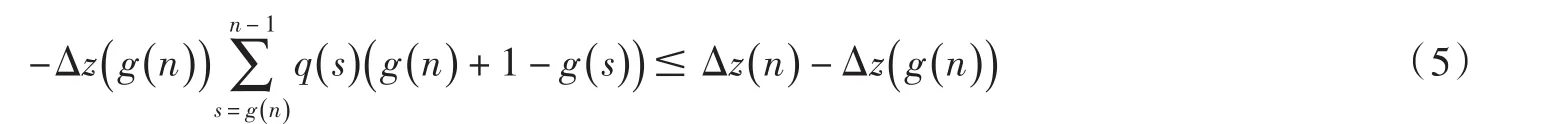
根據 Δz(n ) ≤0及（5）式得

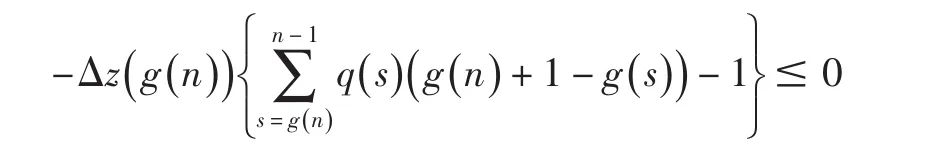
即

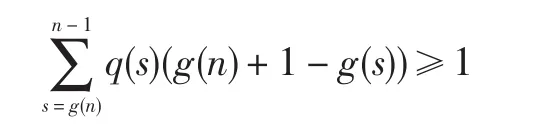
這與（H2）矛盾，故 z()n最終為正也不成立.證畢.

定理3.2假設下列條件成立

（H3）則方程（1）存在有界非振動解x(n)使得

當且僅當

證明假 定x(n ) 是方程（1）的最終有界正解且滿足（6）式，則存在 n1≥n0，當 n ≥n1時，有 Δ2z(n)>0，Δz(n)≤0，從而lin

對（8）式兩端從 s到 ∞求和，得

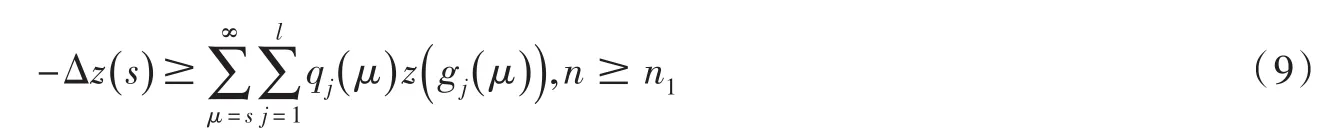
對（9）式兩端從n到∞求和，得因為z()

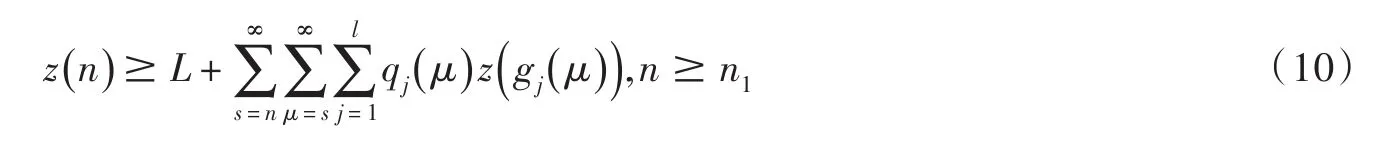
n 有界，由（10）式可知（7）式成立.

下面假定（7）式成立.由（7）式可知，存在充分大的正整數N，使得

記Ω={x ∈ E:1≤x(n)≤2,n≥N-τ}，則Ω是E的有界閉凸子集.定義算子T：Ω→E如下

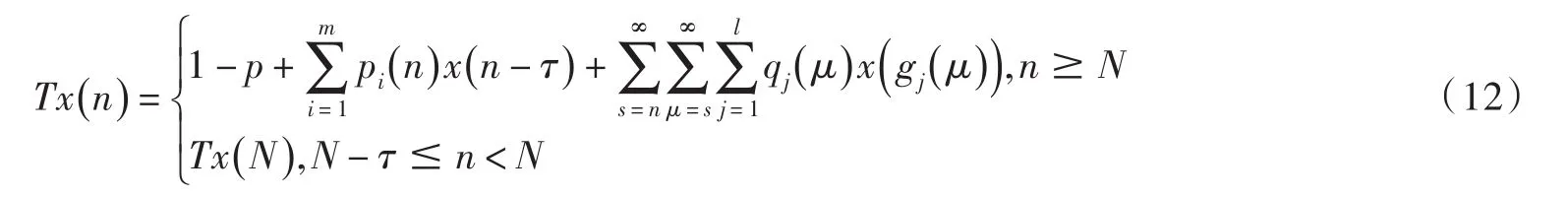
對任意的 x1,x2∈Ω ，當n≥N時，有

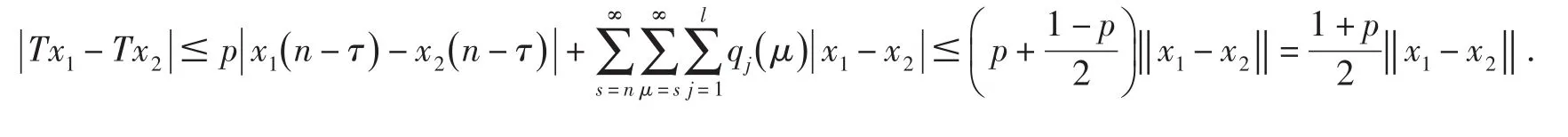
由此得

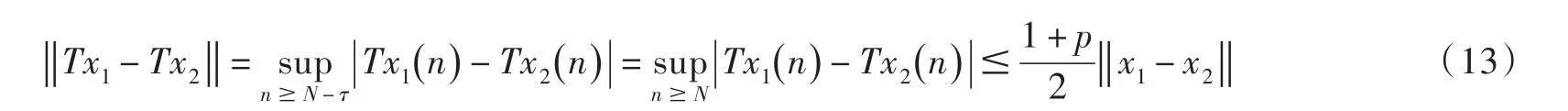
當 N-τ≤n＜N時，對任意的 x1,x2∈Ω ，有（13）式成立.因為所以T為Ω上的壓縮映射，也是連續算子.

對任意的x∈Ω ，當n≥N 時 ，由（11）式 和（12）式 ，得Tx(n)≥1-p+p=1.即1≤Tx(n)＜2.

顯然，當 N -τ≤n＜N時，亦有1≤Tx(n)＜2.因而，Tx∈Ω.即T為Ω上的自映射. 由Banach空間上的壓縮映射原理可知，存在一個x∈Ω，使得Tx=x.由（12）式知，此不動點x滿足

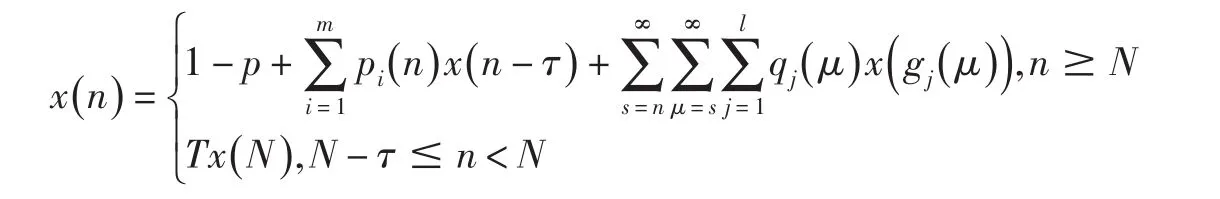
顯然不動點x是方程（1）的一個有界正解且滿足（6）式.

→m∞Δz(n)=0，nl→im∞z(n)=L≠0.

由方程（1）和（2）式及（H3）得

定理3.3…,m,且和

則方程（1）的有界非振動解漸近趨向于零.

證明假 設x(n)是方程（1）的最終有界正解，根據定理3.1的證明知，Δz(n)≤0，z(n)>0最終成立且

若L>0，則存在M>0使得x(n)>z(n)>M ，對方程（1）兩邊從 n0到 n-1求和，得

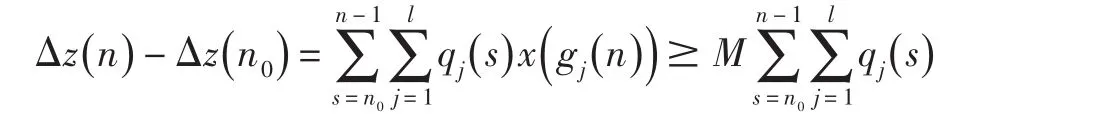
當x(n)為方程（1）的最終有界負解時，同理可證.證畢.

[1]任榮霞，吳淑慧.二階不穩定中立型非線性差分方程有界解的振動性[J].河北師范大學學報：自然科學版，2002，26（2）：118-122.

[2]Zhang Zhengguo,Biping,Dong Wenlei.Scillatory of unstable type second neutral difference equations[J].Korean J Comput Appl Math,2002,9(1):87-99.

[3]孫喜東，劉柏楓，劉曉輝.一類二階中立型差分方程正解的漸近穩定性[J].數學的實踐與認識，2009，39（17）：217-220.

[4]鄭允利，鐘曉珠，張濤，等.二階中立型差分方程非振動解的不存在性和漸近性[J].科學技術與工程，2007，7（21）：5468-5470.

[5]楊甲山.二階變系數多時滯非線性中立型差分方程的正解[J].四川師范大學學報：自然科學版，2009，32（4）：470-473.

[6]邢海龍，鐘曉珠，王東華，等.二階中立型非線性多時滯差分方程有界解的振動性[J].燕山大學學報，2004，28（4）：310-314.

[7]Zhou Yong，Zhang B G.The classification and existence of nonoscillatory solutions of second-order neutral delay difference equa?tions[J].ZAA(Anal Appl),2001,20(1):223-234.