擬人機器人未知環境下穩定行走控制方法

肖 樂，殷晨波，謝從華

（1.常熟理工學院 計算機科學與工程學院，江蘇 常熟 215500；2.南京工業大學 機械與動力工程學院，江蘇 南京 210009）

1 引言

與其他機器人相比，擬人機器人具有更好的行動力，尤其是在不平整地面、斜坡、樓梯等復雜地面上行走時，擬人機器人具有無法比擬的優勢.以往研究穩定行走的方法多是采用離線方式規劃出滿足特定要求的運動軌跡，直接將步態軌跡規劃的理論用于步行實驗[1-2]，這樣做的問題主要有三個方面：一是擬人機器人樣機與機構設計結構總是有一定的誤差，無法精確描述；二是機器人控制驅動系統在復現步態規劃的理論結果時，總有一定的誤差；三是機器人所在的環境，跟步態規劃中的環境模型存在一定的偏差.也有機構采用各種在線修正算法來實現針對實際行走環境的穩定持續行走，步態通過上身位置與時間的對應關系進行調整，通過計算實際值與規劃值之間的差值，所得誤差經過簡單快速處理后得出控制關節所需的扭矩，送回控制系統進行在線步態調節控制[3-7]，但是由于地面條件與理想不符、系統模型不準確、運動學上未考慮的某些非線性因素、動力學方程中各矩陣的計算誤差等原因，很難取得理想的步行控制效果，傳統的維持機器人穩定控制技術大多是基于模型的控制方法，無法得到滿意的軌跡跟蹤效果，導致機器人不能按預先規劃的姿態行走而摔倒[8].本文研究了機器人如何在未知環境下實時調整姿態，包括著地時間控制、落地位置控制和減振控制等方法，很好地控制了機器人的整個行走過程，使機器人時刻保持良好的穩定性.

2 調整控制方法

2.1 落地時間控制

在機器人的行走過程中，擺動腿的落地時間是在步態規劃時所設置的.但是步態規劃是在假定地面絕對水平的前提下進行的，它并不是機器人在真實行走中的落地時間.因此，有必要對落地時間進行補償.傳統的落地時間控制僅僅是在擺動腿根據步態規劃的著地時間還沒有和地面接觸時，延緩行走步態流程.這種落地時間的滯后是由于地面的局部傾斜使得機器人向外傾斜所致.相反，如果機器人向內傾斜，它將在預期時間之前著地來防止跌倒，如圖1所示.

在機器人向外傾斜的情況下，如果機器人不跌倒，那么只須延緩步態流程直到檢測到擺動腳底的地面反作用力為止.然而，如果機器人是向內傾斜，就必須被提前檢測到.在左右髖關節各裝一個x方向的陀螺儀，可以通過角速度補償落地時間.x方向的角速度由陀螺儀測得，左腿支撐期由左髖關節的陀螺儀測得，右腿支撐期由右髖關節的陀螺儀測得.

當角速度由正變負或由負變正時，往往發生在擺腿擺到最高點的時候.如圖2所示，x軸代表時間，y軸代表陀螺儀的轉速或擺動腿的擺動高度.為了方便起見，角速度用直線表示（見圖3）.在通常情況下，機器人身體側向擺動的角速度會在A和B之間穿過x軸，因為骨盆側向位移方向的改變與擺動腿達到最高點會有一個時間的滯后.如果機器人向內傾斜，則髖關節的角速度會在A點之前穿過x軸.這時，就需要提前降低擺動腿.其原理闡述如下：1.在步行周期的第一或第三個階段，通過測量x方向的角速度得到角速度曲線穿過x軸的點.2.如果這個點在A和B之間，說明機器人不會提前著地.機器人可以規劃的軌跡正常行走.3.如果這個點發生在比A點早△t的時間點，就使擺動腿提前△t的時間著地.

用這種方法能夠優化機器人的著地時間，使機器人每一步的落地時間都是最佳時間，機器人就能穩定行走.

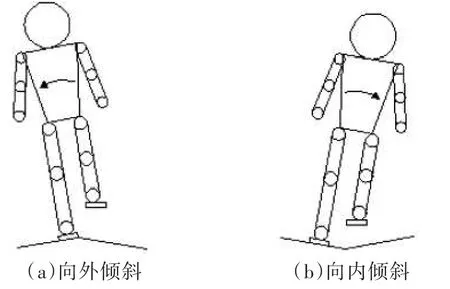
圖1 機器人傾斜情況

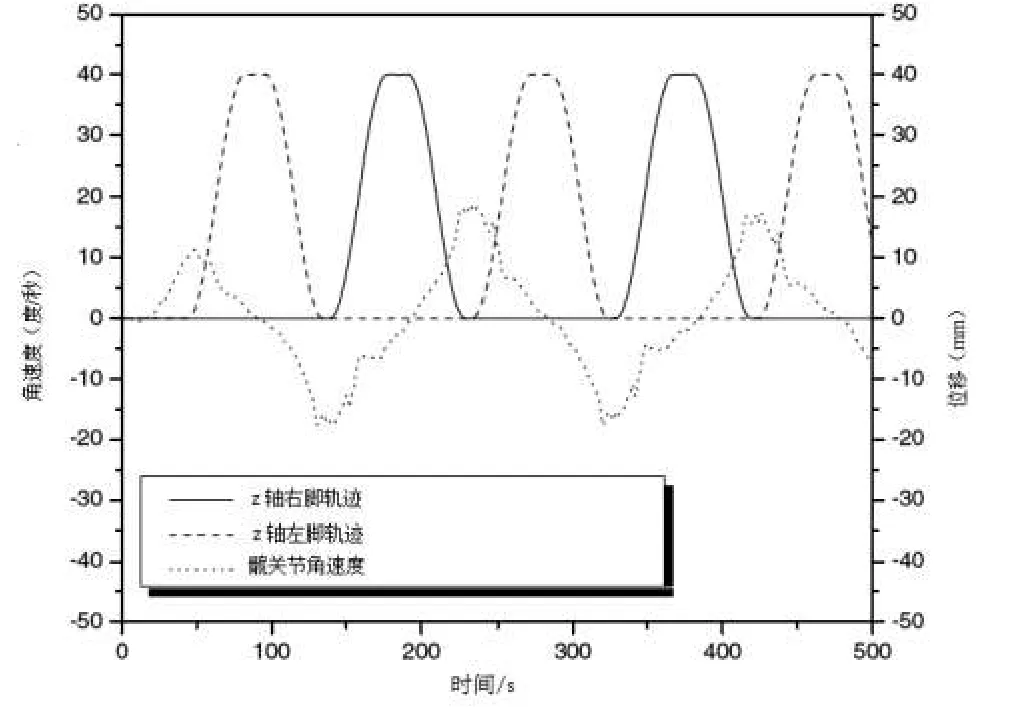
圖2 髖關節角速度和擺動腿軌跡

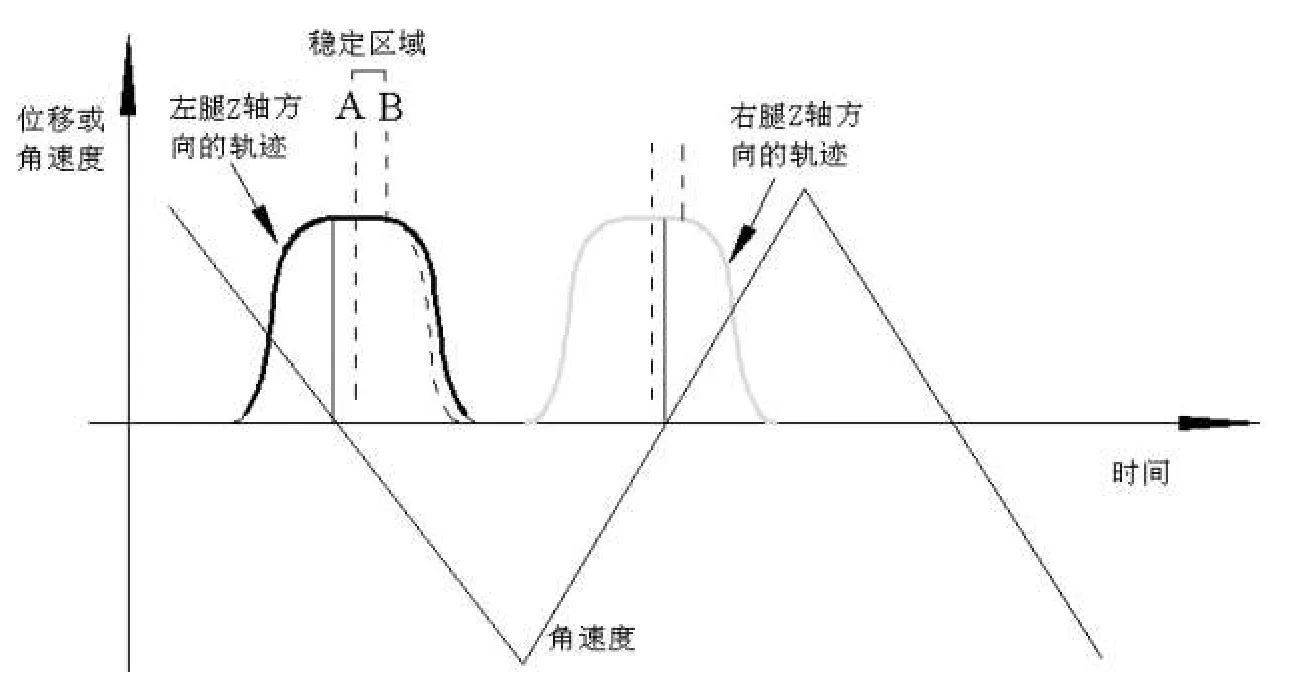
圖3 落地時間控制

2.2 落地位置控制

和落地時間相似，落地時間補償也很重要.機器人的落地時間和落地位置在機器人的行走過程中是很重要的兩個因素，因為機器人行走最終實現的就是這兩個因素.首先考慮人類的行走，落腳點是連續變化的.這一現象表明人們通過使用前庭器官來產生到達期望落地點所需的角動量.例如，如果落地角速度太大，那么我們會把步子跨大點，使落地點遠離身體重心來減小著地時的角速度.同樣的，擬人機器人也需要通過傳感器的反饋控制對預期著地點進行調整，優化實際的落地位置.我們可以通過角動量在落地前補償著地位置，使得機器人的擺動腿在合適的位置著地.

圖4是機器人在著地前和著地后的狀態.公式（1）用沖擊模式來表示機器人的落地模式.

其中，ωBL是落地前瞬時的角速度，ωAL是落地后瞬時的角速度，I是相對于支撐點的慣性矩，M是擺動腿開始著地時作用于踝關節的力矩，Δt是M的作用時間，IωAL是落地后瞬時的期望角動量，IωBL是落地前瞬時測得的角動量.因此，有必要用 MΔt對IωAL進行調節，因為IωBL是隨著機器人的行走而變化的.公式（1）可以寫成如下形式：

其中，Ma是擺動腳剛開始落地時由地面反作用力作用在踝關節的力矩，mgd由重力作用在踝關節的力矩.因此，落地點d，也就是距離身體中心的距離可由下式得到：

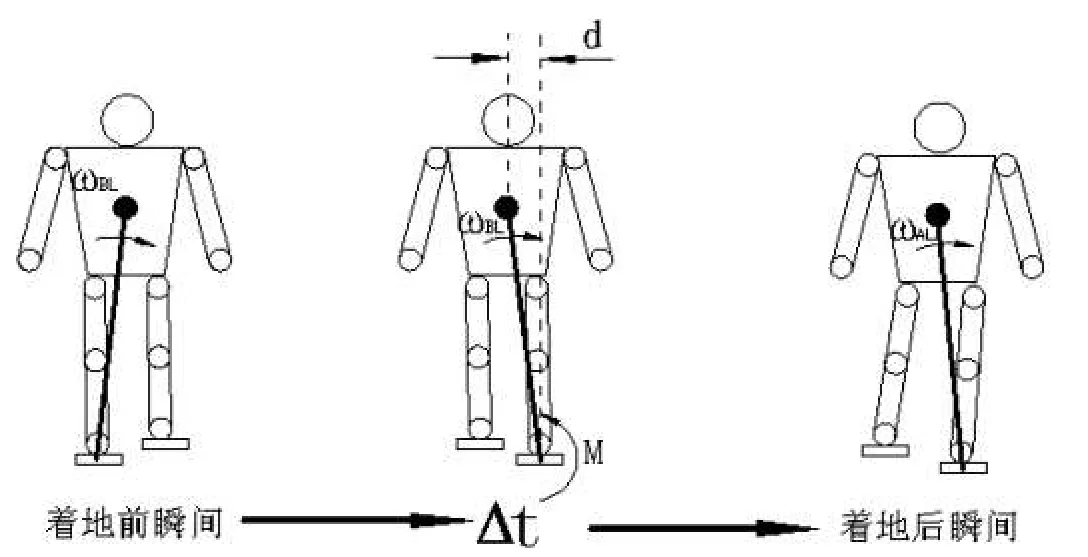
圖4 落地位置控制

然而，實際上d是由步態規劃所決定的.如果我們把預期的落地點記為dpre，那落地點的補償量就可由d和dpre之差乘上一個比例增益kp得到.最終的落腳點dfinal就可以由dpre加上這個補償量得到.

2.3 減振控制

當機器人行走的時候，擺動腿會有一定的振動.這是由于腿和盆骨之間的框架會有一定的偏斜，而且減速齒輪存在很小的齒側間隙.這個振動量并不大，但會影響到落腳點精度的控制.如果落地點控制的精度超出了±3 mm的范圍，落地點控制器將不能很好地發揮作用.因此對落地點位置控制來講，減振是必需的.

圖5是擺動腿的數學模型，u是輸入的髖關節角度，θ是實際髖關節角度，m是腳的質點，l是從質點到髖關節的距離，k是彈簧的扭轉剛度.系統的運動方程可以表示為

圖5 擺動腿數學模型

傳遞函數可以表示為

以上的傳遞函數是一個在拉普拉斯域的虛軸上有兩個極點的邊界穩定系統.通過靜態單腳支撐期的擺動腿的三個實驗可以求得振動周期，從而得到k/ml2.

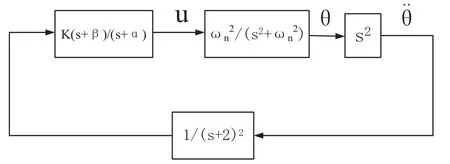
圖6 減振控制框圖

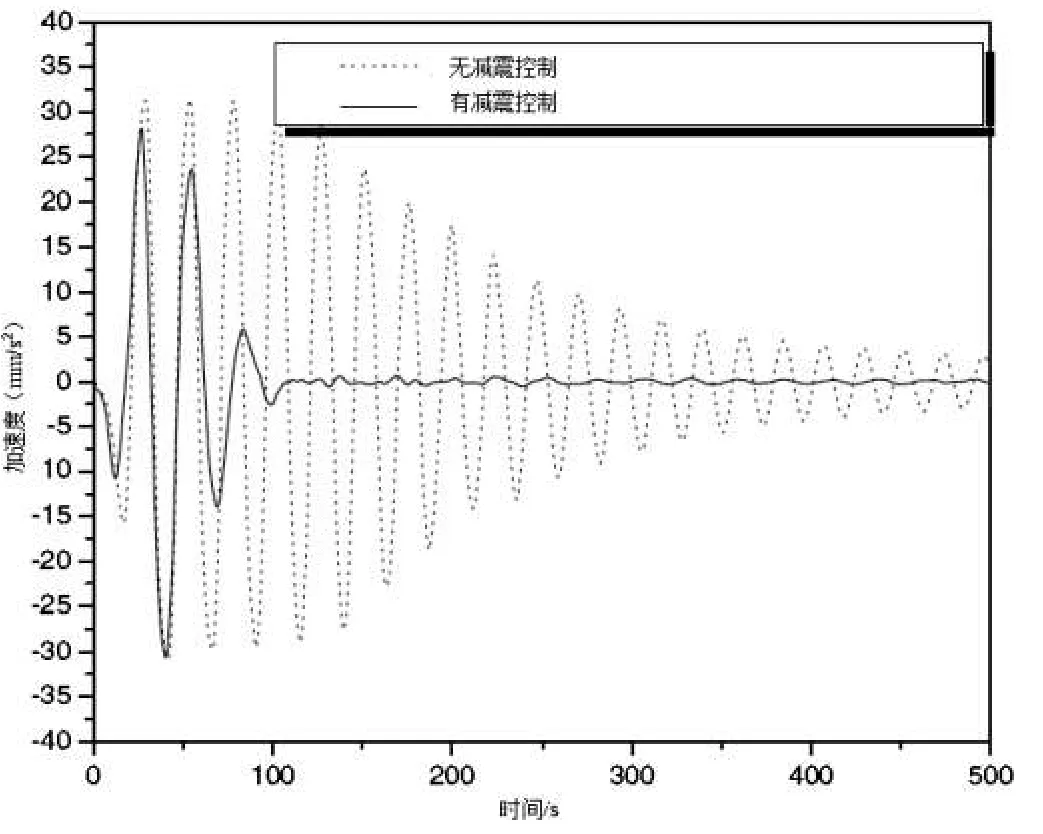
圖7 擺動腿的自由振動響應

3 結束語

本文對擬人機器人雙足穩定行走控制方法進行了深入研究，提出擬人機器人在復雜環境中如何通過落地時間控制、落地位置控制和減振控制等方法，使機器人獲得新的支撐區域，恢復穩定，提高穩定行走能力，為實現擬人機器人實時控制奠定了基礎.

[1]Harada K,Kajita S.Real-Time Planning of Humanoid Ro?bot's Gait for Force Controlled Manipulation[C].New Or?leans:Proceedings of the 2004 IEEE International Confer?ence on Robotics and Automation,2004:616-622.

[2]Eaton M,Thomas J,Davitt.Evolutionary Control of Bipedal Locomotion in High Degree-of-freedom Humanoid Robot:First Steps[J].Artificial Life and Robotics,2007 11(1):112-115.

[3]付根平，楊宜民，陳建平，等.基于ZMP誤差校正的擬人機器人步行控制[J].機器人，2013，35（1）：39-44.

[4]J H Kim,J H Oh.Walking Control of the Humanoid Platform KHR-1 based on Torque Feedback Control[C].New Orleans:Proceed?ings of the 2004 IEEE International Conference on Robotics and Automation,2004:623-628.

[5]陳磊，張國良，張維平，等.基于模糊控制的擬人機器人零力矩點在線調整[J].計算機應用，2013，33（SI）：298-300.

[6]Napoleon,Nakaura S,Sampei M.Balance Control Analysis of Humanoid Robot based on ZMP Feedback Control[C].Lausanne:Pro?ceedings of the 2002 IEEE/RSJ International Conference on Intelligent Robots and System,2002:2437-2442.

[7]肖樂，常晉義，殷晨波.仿人機器人穩定性分析[J].常熟理工學院學報，2011，25（2）：109-112.

[8]胡凌云，孫增圻.擬人機器人步態控制研究方法綜述[J].計算機研究與發展，2005，42（5）：728-733.