數學教學中如何設計問題

歐瑞娟

【摘要】 問題是學生學習的拐杖，適合學生的學習水平的問題，能正確的引導學生學習，來開發學生的智力。喚起學生的思維，激發學生的求知欲望，把學生學習引向深入，使學生覺得學習數學并不是高不可攀的。

【關鍵詞】 問題 智力 思維 激發 引向深入

【中圖分類號】 G633.6 【文獻標識碼】 A 【文章編號】 1992-7711（2015）02-087-01

眾所周知，問題是學生學習的拐杖，適合學生的學習水平的問題，能正確的引導學生學習，來開發學生的智力。喚起學生的思維，激發學生的求知欲望，把學生學習引向深入，使學生覺得學習數學并不是高不可攀。那么在數學教學中，如何設計適應學生水平的問題呢？我的做法是：

一、根據教材設計問題，突出教材的重點、難點

每節數學課都有其重點、難點。問題必須體現本節課的重點、難點，這就要求教師認真備課，做到三點，第一，要了解每節課的知識框架，體系脈絡，主要矛盾以及重難點。第二，要研究知識的內涵外延，這些知識在形成過程中的思維過程；第三，要了解學生的各類思維品質和知識基礎，教師要設身處地，反復揣摩，學生自學時哪些難懂，哪些容易混淆，哪些知識前呼后應，怎樣設置情景，激發學生的求知欲望，凡是學生在思考中可能遇到的問題要盡可能估計到。

問題要淺顯詳說，根據課文逐段偏寫，讓學生在書上直接找到答案，這樣有利于學生準確的理解課文，有利于激發學生的興趣調動學生的積極性，如學習“解一元一次方程”一節時，我設計的問題是：

問題1：某校三年共購買計算機140臺，去年購買數量是前年的2倍，今年購買數量又是去年的2倍。前年這個學校購買了多少臺計算機？

導入設計如下：

1. 題中含有怎樣的相等關系？

2.應怎樣設未知數，如何根據相等關系列出方程？

問題2：方程x+2x+4x=140在結構上有什么特征？

問題3：怎樣才能將它轉化為x=a（a為常數）的形式呢？

問題4：合并同類項的依據是什么？

問題5：以上解方程中“合并同類項”起了什么作用？

在教學過程中，通過提問的方式，小組搶答打分制度，引導學生一步一步讀題，提取題目中的重要信息，整理成一個列方程的相等關系，學生的表現都很積極，活躍。

隨著學生的解題能力的提高，問題要由淺顯詳細轉向概括簡略，富有啟發性思考性，一般不能從書上直接找到答案，需要學生觀察、比較、議論、概括才能解答提問中的問題；這有利于自學能力的培養。

二、設計問題要由淺入深循序漸進

學生認識事物的規律由淺入深循序漸進，按照這一規律設計問題，能使學生一步一步的深入思考，把學習逐步引向深入。如學習“銷售中的盈虧”一節

我設計的問題是：

問題1：標價為200元的服裝7折銷售，現在購買需要多少錢？如果這種服裝的成本是115元，賣出一件商家能賺多少錢？獲利率是多少？

導入設計如下：

1. 這個問題講的是什么情境？

2. 這個問題出現了哪幾個商業用語？商業用語的含義？

3. 商品銷售問題基本的等量關系有哪些？

4. 你能計算這道題嗎？

問題2：某件商品的進價是40元，賣出后盈利25%，那么利潤是多少？如果賣出后虧損25%，利潤又是多少？

導入設計如下：

（1）盈利與虧損是一對怎樣的量，

（2）盈利怎樣記；虧損怎樣記？

問題3：某商店在某一時間以每件60元的價格賣出兩件衣服，其中一件盈利25%，另一件虧損25%，賣這兩件衣服總的是盈利還是虧損，或是不盈不虧？

導入設計如下：

（1）你認為是虧還是盈？還是不虧不盈？能說一下理由嗎？

（2）判斷是盈利還是虧損的主要依據是什么？

（3）你能求出探究問題中的兩件物品的進價嗎？

（4）你能分析總的虧損情況嗎？

（5）回顧反思：解決銷售盈虧問題的一般思路及判斷虧盈的依據

學習問題探究時先讓學生猜一猜總的盈虧情況，采用自由發言的方式，目的是讓學生說出真實的想法調動學習的積極性，以便把問題引向深入。

三、設計問題要富有啟發性思考性

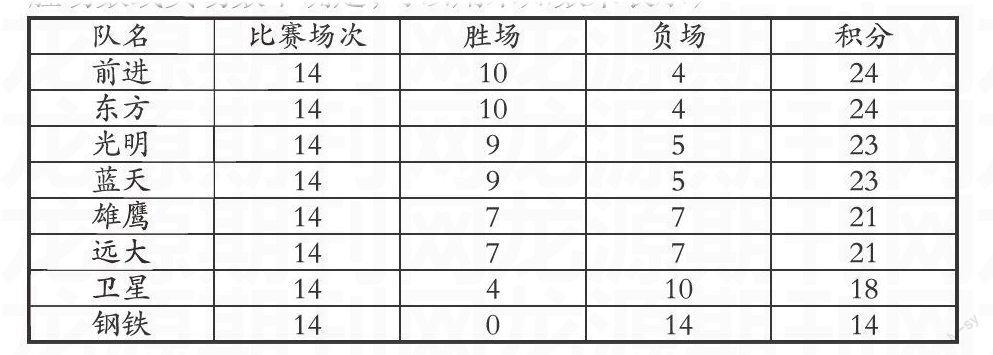
問題是扶著學生走，問題的指導作用在于體現教材的重點、難點，問題的編寫應具體、富有啟發性、思考性，要注意與舊知識的聯系和知識的鋪墊，精心的設疑，以疑啟思，這樣有利于培養學生的思維能力，鍛煉學生思維的廣闊性，深刻性。例如學習“球賽積分表問題”

我設計的問題是：

問題1：從這張表格中，你能得到什么信息？

問題2：這張表格中的數據之間有什么樣的數量關系？

問題3：請你說出積分規則。（既勝一場得幾分？負一場得幾分？）你是怎樣知道這個比賽的積分規則的？

問題4：列式表示積分與勝、負場數之間的數量關系（提示：勝場數或負場數不確定，可以用未知數來表示）

問題5：有沒有某隊的勝場總積分能等于負場總積分。

問題：通過對球賽積分表的探究，你有什么收獲？

設計了系列梯度較小的問題，引導學生觀察思考，學習如何從表格中獲取數據信息，挖掘題目中隱含的數量關系，進而列出方程解決問題。

四、設計問題不能拘泥于教材，要緊密結合知識結構的內在聯系和學生認識結構的發展趨勢

例如學習“圓和圓的位置關系”這一節。我設計的問題是：

問題：圓和圓的位置關系由什么決定、與哪些元素有關系？

充分發揮學生的想象力和探索精神，通過大家的討論及動手、動腦、分折、歸納得出三個方面：用度量關系判斷，②移動二圓從運動的觀點判斷，③利用三角形三邊關系判斷。這些都不是書上提出的，是通過讀書、思考、探討、尋找出的方法、使學生樹立自信培養了創新意識。

總之問題就像一條紅線，自始至終貫穿在教學中，開始需要問題引路，學習中需要問題的指向思考，無論是教師的輔導還是練習中出現的問題，都要歸結到是否完成了問題，小結時，又要以問題的要求來檢查落實的程度，鞏固和深化教學效果。只要老師長期堅持設計好問題學生就會懂得問題的重要性。