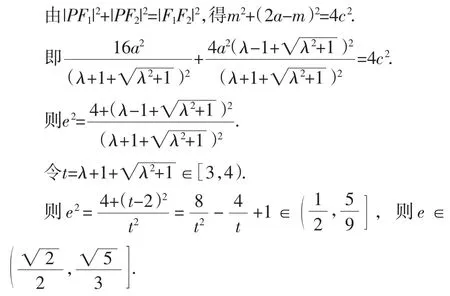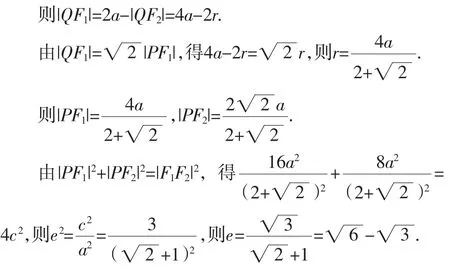來自高考數學閱卷場的報告
——2015年重慶卷考生答題分析與教學建議

☉重慶市教育科學研究院 張曉斌

☉重慶市南岸區教師進修學院 肖 飛

☉西南大學數學與統計學 院江楠

來自高考數學閱卷場的報告
——2015年重慶卷考生答題分析與教學建議

☉重慶市教育科學研究院 張曉斌

☉重慶市南岸區教師進修學院 肖 飛

☉西南大學數學與統計學 院江楠

今年重慶市高考數學試卷結構、分值、試題特點與去年相似，但試題整體難度有所下降，估計理科平均分接近100分，文科平均分接近90分.由于選擇題是機器閱卷，因此我們主要針對考生對解答題的解答情況作出分析，并給出教學建議.

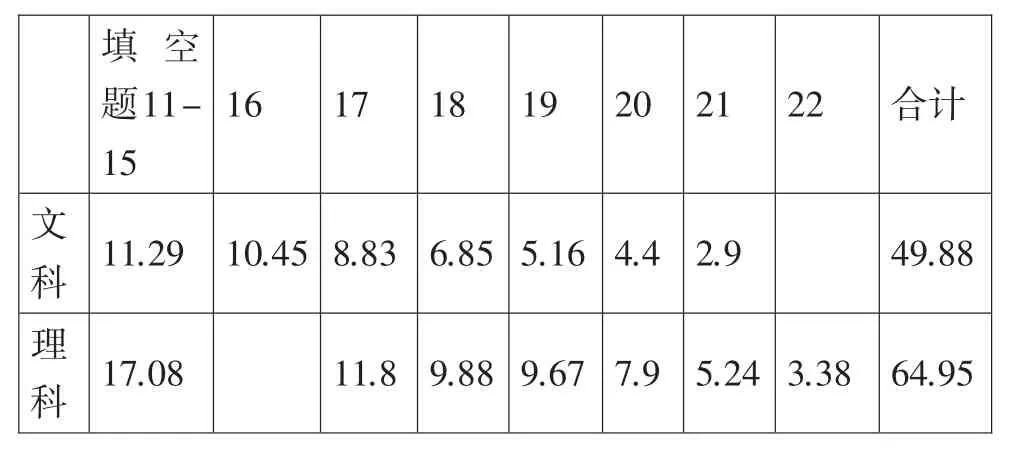
今年文理科填空題、解答題平均分統計表

?

這些數據說明今年重慶高考數學試題難度控制較為合理，并且試題能較好地區分出數學學得很好、好、中、差、很差的學生，體現了較好的區分度，從而達到選拔各層次人才的目的.

一、有關數列問題的解答情況分析

1.正確解法

文科數列題是文科第一道解答題，除了參考答案以外，學生還用到了以下解法.

（1）利用等差數列的性質.

（2）利用等差數列的通項公式與前n項和公式.

理科數列題是理科最后的壓軸題，學生除了參考答案以外，還用到了如下解法.

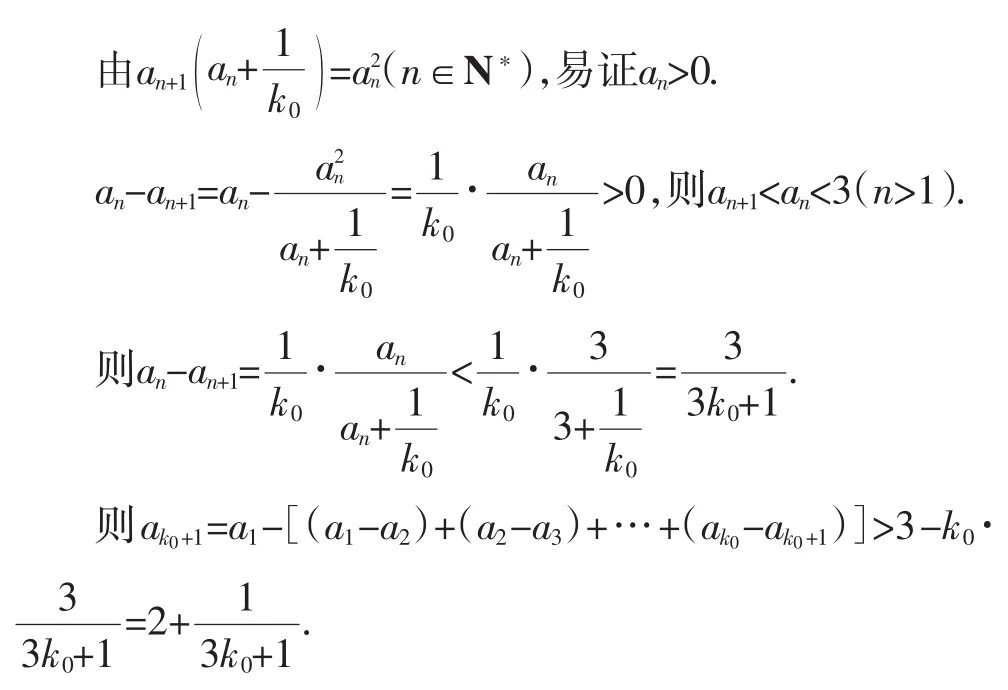
另一方面a1>a2>…>ak0+1>2.

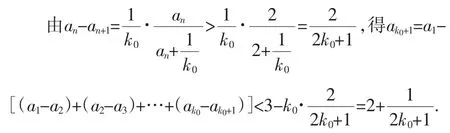
2.典型錯誤

在解答過程中，文科學生出現的典型錯誤有以下幾種.

④審題不仔細，如第二問求出通項后，沒有求出前n項和.

理科學生出現的典型錯誤有以下幾種.

①在第一問中，把等比數列的公比和首項求錯，用錯通項公式；

②在第二問中，利用數學歸納法驗證首項時錯把“k0=2”驗證為“k0=1”；

3.教學建議

文科要重視基礎知識的學習，加強基本公式的記憶及運算，重視驗算步驟的書寫和規范.理科除此之外，還應強化數列與不等式的綜合應用.

4.試題評價

數列題作為文科第一道大題，難度較小，主要考查學生對公式的記憶及運算能力；數列題作為理科最后一題，不但考查了等比數列求通項等基礎知識，還考查了學生的推理論證能力和創新意識，綜合性較強，涉及不等式放縮法、數列的單調性、累加法等，區分度非常明顯，是選拔能力型人才的一道好題.

二、有關概率統計問題的解答情況分析

1.正確解法

文科考查的是線性回歸直線方程及其應用，除了參考答案以外，學生還用到了以下兩種方法.

法2：調查另一組數據ti′=ti-3，yi′=yi-7，減小計算量，提高準確率.

理科考查的是概率與數學期望的計算，是理科第一道解答題，除了參考答案以外，學生還用到了以下方法.

法3：第二問利用分類討論：

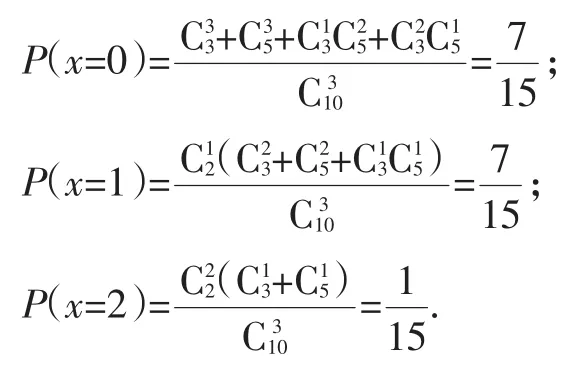
2.典型錯誤

在解答過程中，文科學生出現的典型錯誤有以下幾種.

②不理解求和符號的意義，如：

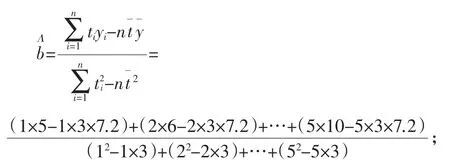
③計算步驟過于簡陋，影響得分.

理科學生出現的典型錯誤有以下幾種.

②第二問用分類討論方法時，漏掉某些情況；

③題意理解不清楚，錯當為獨立重復試驗的二項分布處理.

3.教學建議

對文科學生要強化計算能力，提高計算水平；細化大題書寫過程的規范性，詳略得當以增強得分點.對理科學生要加強基本概念教學，即基本事件、互斥事件、獨立事件、獨立重復試驗等的教學，注重分類討論思想方法的培養，做到不重、不漏.

4.試題評價

文科第17題難度不大、考點單一，主要考查學生的運算能力.理科第17題難度較小，主要考查學生利用組合數求解古典概型、計算分布列和數學期望的能力.

三、有關三角問題的解答情況分析

1.正確解法

文、理科三角函數解答題是一道姊妹題，除參考答案外，文科學生用到了以下解法.

法1：直接化簡求值.

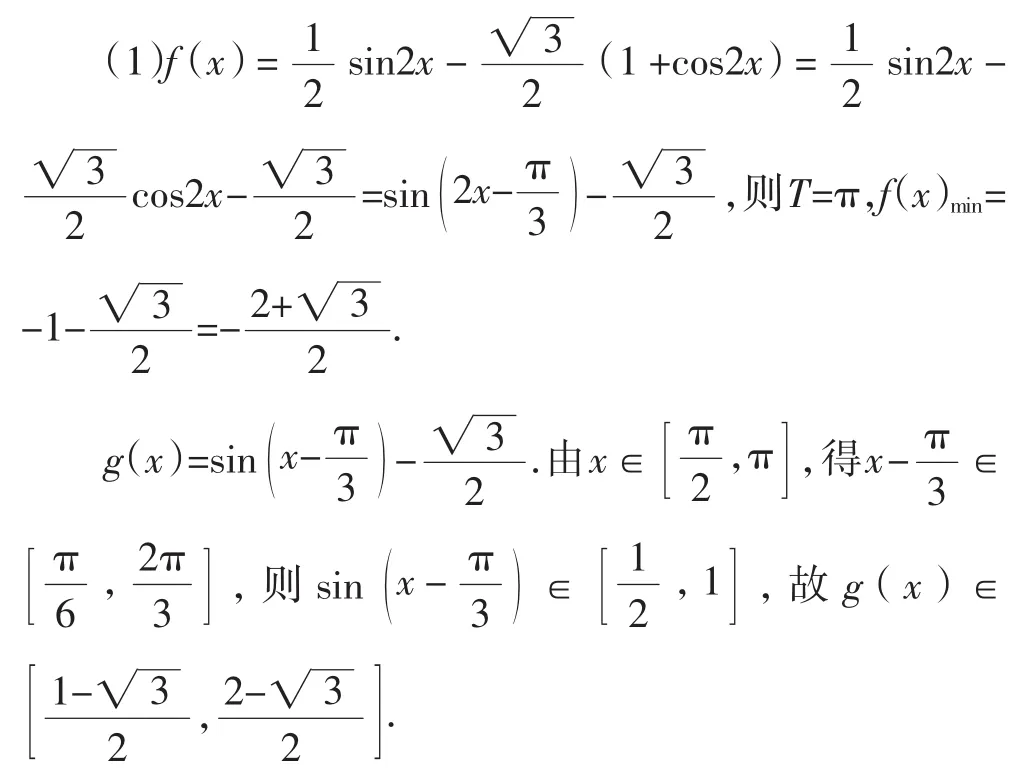
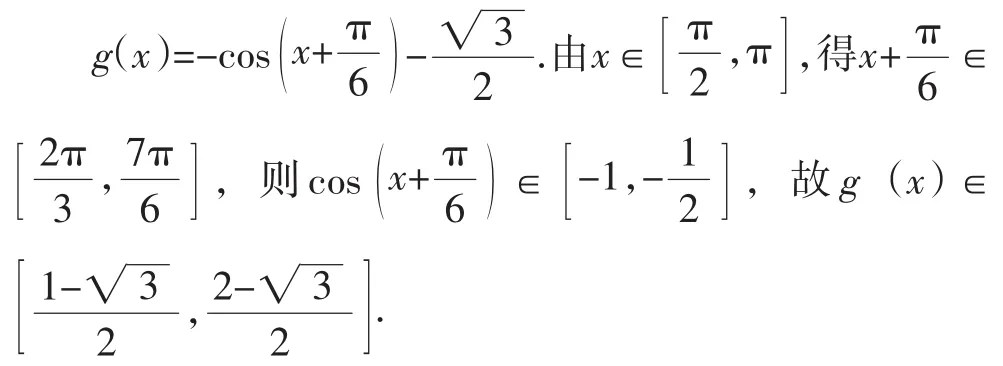
法2：在第二問中，直接通過圖像的變換畫出平移、伸縮前后的圖像來求值域.

法3：在第二問中，利用求導或其他方法先求出單調區間，再求解值域.

理科三角函數解答題，除了參考答案以外，學生主要用到了以下解法.

法1：利用配湊二倍角公式來化簡.

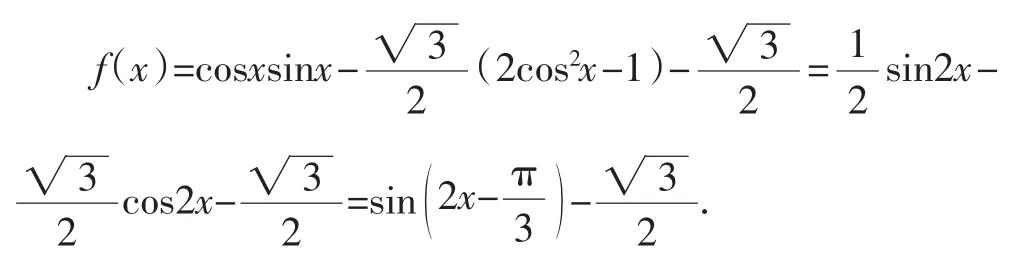
法2：利用積化和差公式來化簡.

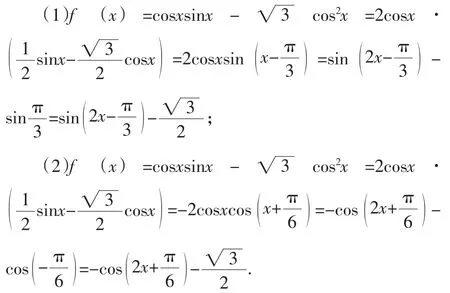
法3：先求函數在整個定義域上的單調區間，再與所需區間取交集.

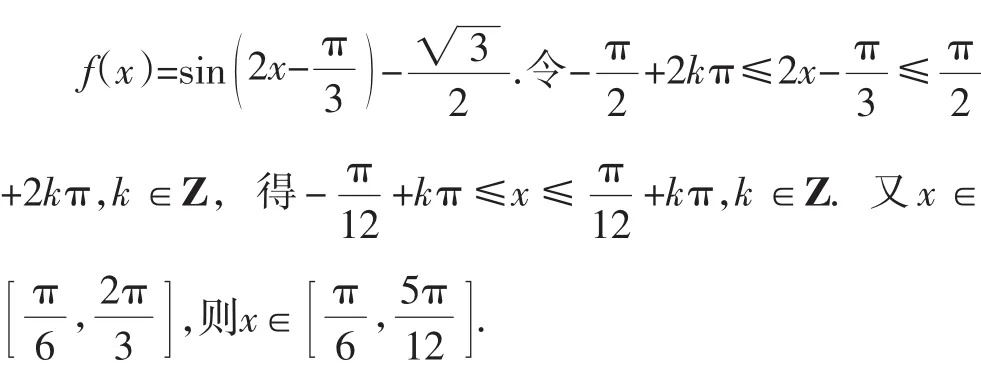
2.典型錯誤

在解答過程中，文科學生出現的典型錯誤有以下幾種.

理科學生出現的典型錯誤有以下幾種.

①根本就不會化簡；

⑤簡單地代入區間端點值來求值域.

3.教學建議

加強文、理科學生的基本功訓練，主要體現在基本公式、基本計算上，重視通性、通法的培養，提高學生嚴密的數學思維能力，規范學生的數學學習習慣和書寫習慣.

4.試題評價

此題涵蓋了三角函數化簡、圖像及性質，其中化簡變形具體涉及了誘導公式、降冪公式、二倍角公式、輔助角公式、三角函數的性質等，還涉及了三角函數的值域、單調性及圖像的變換，全面考查了三角函數的基本知識和基本技能，難度適中.

四、有關函數與導數問題的解答情況分析

1.正確解法

文科函數與導數解答題，學生出現的有別于參考答案的解法如下所示.

由f′（x）=3ax2+2x，得

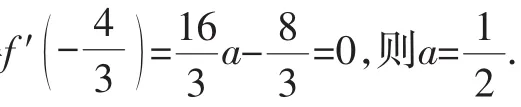
由g（x）

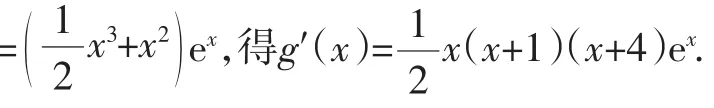
令g′（x）>0，得x∈（-4，-1）∪（0，+∞）.

則g（x）在（-4，-1）和（0，+∞）上單調遞增，在（-∞，-4）和（-1，0）上單調遞減.

理科函數與導數解答題除參考答案外，學生還出現了以下解法.

法1：分離參數法.

當x∈［3，+∞）時，g′（x）<0，則g（x）在［3，+∞）上單調遞減，則

法2：構造函數法（數形結合）.

（1）令h（x）=-3x2+（6-a）x+a，則h（x）≤0?x∈［3，+∞）恒成立.

（2）令h（x）=-3x2+（6-a）x+a，則h（x）≤0?x∈［3，+∞）恒成立.

（3）-3x2+（6-a）x+a≤0，則-3x2+6x≤a（x-1）?x∈［3，+∞）恒成立.

令h（x）=-3x2+6x，記A（1，0）、B（3，-9），由圖可知a≥ kAB，則a≥

2.典型錯誤

在解答過程中，文科學生出現的典型錯誤有以下幾種.

①不會求導（或算錯），包括對簡單多項式求導和兩個函數的乘積求導；

②不清楚極值點與導數為0的關系；

③錯用單調性運算性質求單調區間，如：因為ex>0且單調遞增，所以g（x）的單調性與f（x）的單調性相同，所以只需求f（x）的單調區間；

④不會解高次不等式.

理科學生出現的典型錯誤有以下幾種.

①第一問中，除法求導法則運用錯誤多，不少學生在運算中將符號弄錯；

②第二問中，求一個新函數的最值時步驟嚴重缺失，如未求導、不判斷單調性，直接寫出最值；

③第二問中，分離參數時不等號方向弄錯；

④構造函數法（數形結合）的第一種解法中，漏掉第二種情況，或第一種情況條件不全.

3.教學建議

加強對函數與導數章節中各個公式的理解記憶，回歸教材、落實基礎；加強第一步求導的重要性意識的樹立，提高運算能力，重視通性、通法的培養；加強數形結合、分類討論、問題轉化等重要數學思想與方法的滲透教學；重視本章節知識網絡體系的構建.

4.試題評價

本題考查用導數解決函數問題的基本方法與基本技能，知識點覆蓋全面，涵蓋求導、極值、切線方程、單調區間等基本問題，還有恒成立問題.此題入口很寬、深入較易、方法常規，注重通性、通法，也有一定的區分度，需要考生們仔細審題、嚴謹分析、仔細計算.文科解答題涉及了高次不等式的求解，運算難度提高，區分度好.

五、有關立體幾何問題的解答情況分析

1.正確解法

對于空間立體幾何解答題，文科學生除了參考答案以外，還用到了以下幾種思路.

又a2+b2=36，則b=3或即BC=3或

法2：作DH⊥AB于H點，設DH=x，則EF=2x，AB=

SBCDF=S△ABC-S△ADF

理科學生除了參考答案以外，還用到了以下思路.

法2：以D點為坐標原點，DE、DC所在直線為x、y軸，建立空間直角坐標系.

法3：利用三垂線定理找到二面角.

由VP-ACD=VC-PAD，得點C到平面PAD的距離

（2）過A作AO⊥CD于點O，過O作OM⊥PD于點M，連接AM.

法4：利用面積射影定理求二面角的余弦值.

過A作AO⊥CD于點O，易證AO⊥面PCD，則△POD為△PAD在面PCD上的射影，經計算

2.典型錯誤

在解答過程中，文科學生出現的典型錯誤有以下幾種.

①在第一問的證明過程中，證明條件不完整，主要是由面面垂直推導線面垂直時出現問題；

②在第一問的證明過程中，跳躍太大，直接由面面垂直就得到線線垂直了；

④在第二問中，算出兩個值，但是由圖觀察BC

⑤在第二問中，以EC、EP、EF為坐標軸建立錯誤的空間直角坐標系；

⑥運算錯誤，有的直接計算體積，也有的將所求四棱錐切割成兩個三棱錐（以△DCF、△BCF為底面）或者一個三棱錐、一個四棱錐（以△DEF、四邊形BCEF為底面）.

理科學生出現的典型錯誤有以下幾種.

①計算錯誤，一是計算AC的長度出錯，從而A點的坐標出錯，進而平面PCD的法向量算錯，二是D點坐標算錯，導致平面PAD的法向量算錯；

②在第一小問中，證明時邏輯不清，對定理使用條件不清：一是誤證D→E與平面PCD的法向量垂直（本該證平行），二是在證明DE⊥DC與DE⊥PC兩垂直關系時邏輯不清，三是利用面PCD⊥面CDE去證DE⊥面PCD時，對定理使用條件不清不楚；

③對利用法向量計算二面角時，到底算的是二面角還是其補角含糊不清.

3.教學建議

立體幾何教學要重視“雙基”教學，加強運算能力的培養，強化訓練學生對立體幾何中線線、線面、面面平行與垂直證明的邏輯推理能力，及相關性質與判定定理條件的使用與記憶能力；重視對傳統幾何方法的教學，以增強學生的空間想象力、邏輯推理能力；加強對向量法建系的坐標軸與頂點的選擇性訓練，切實訓練學生規范作答的習慣.

4.試題評價

文科試題以三棱錐為模型，考查了學生線面垂直判定定理和面面垂直性質定理的運用，注重考查學生的空間想象能力和邏輯推理能力，第二小問中既考查了學生“分割”、計算等能力，又體現了方程思想與立體幾何的完美結合，題面較新穎，又有很好的區分度，是一道不可多得的好題.理科試題主要考查了線面垂直的證明及二面角的計算，這也是歷年考試的熱點，體現了優化思維、簡化運算的思想，考查了學生的推理能力與計算能力，體現了立體幾何的基本思想.作為第三道解答題，難度適中，得分率高.

六、有關解析幾何問題的解答情況分析

1.正確解法

文、理科解析幾何解答題是一道姊妹題，除參考答案外，文科學生主要有以下幾種思路.

法1：第一問利用定義求出a，再利用勾股定理或焦點三角形面積公式算出c，進而求得橢圓方程.

法2：設|PF1|=m，|PQ|=λm，則|F1Q|2=（λ2+1）m2?|F1Q|=

法3：設|PF2|=m，|F2Q|=n，則|PF1|=2a-m，|F1Q|=2a-n.

由|PF1|2+|PF2|2=|F1F2|2，得m2-2am+2b2=0?m=a±

理科試題除了參考答案以外，學生還用到了以下解法.

法1：設|PF1|=r，則|PF2|=2a-r，|QF2|=|PF1|-|PF2|=2r-2a.

法2：以F2為極點，射線F2x為極軸，建立極坐標系，設∠PF2x=θ，則則|PQ|=

由|PQ|=|PF1|，得2（1-esinθ）=1-e2cos2θ.

由|PF1|+|PF2|=2a，得e（sinθ+cosθ）=1，則1-esinθ= ecosθ.

則2ecosθ=1-e2cos2θ，則則esinθ=1-則

法3：設P（x1，y1），Q（x2，y2），由第二定義得|PF1|=a+ ex1，|PF2|=a-ex1.

由PF1⊥PF2，得x21+y21=c2，則y21=c2-x21.把直線PQ的方程代入橢圓標準方程并化簡，得［b2（x1-c）2+

則|PQ|=2a-e（x1+x2）

由y21=c2-x21，得

2.典型錯誤

在解答過程中，文科學生出現的典型錯誤有以下幾種.

①第一問利用勾股定理時算錯；

②常量a、c的意義混淆；

③設直線PQ的方程時利用第一問錯誤的c值；

④聯立橢圓和直線PQ的方程消元，利用韋達定理算弦長，無法完成計算.

理科學生出現的典型錯誤有以下幾種.

①求橢圓方程時，將b、c算反；

②在第一問中，沒有想到用橢圓的定義求a；

③在第二問中，用設點或設直線的方式解題，導致運算量巨大，無法完成計算.

3.教學建議

對本題教學中要注重“雙基”，突出基本概念的理解和應用；注重解析幾何中平面幾何知識的應用；加強數形結合、轉化與化歸、函數與方程等數學思想與方法的運用，同時注重運算能力的培養.

4.試題評價

本題是文科最后的壓軸題，重點考查了橢圓的定義，利用定義求橢圓方程，利用定義將幾何條件代數化，建立方程，再利用方程與函數思想求出值域.此題立意好、思路新穎，對學生的思維能力、運算能力、綜合能力要求都極高，是一道非常出色的題，有相當高的區分度，是選拔優秀人才的好題.本題作為理科倒數第二題，考查學生在解析幾何中運用平面幾何知識解決問題的能力，難度適中，切入點巧妙，將橢圓的定義與平面的勾股定理有機結合在一起，考查了學生數形結合、轉化與化歸、函數與方程等數學思想，回避了解析幾何中“硬算”的特點，考查了學生靈活應變的能力，有較大的區分度.

總之，從以上分析來看，對于立體幾何與解析幾何試題，學生解法思路多，但發生的錯誤也多，說明學生易入手，得高分難，想得到做不到，突出的問題是基礎知識不扎實，基本技能不過硬.從全卷學生的答題情況來看，通篇表現出學生“根基”不牢，一看就會，一做就錯，成為常態.但凡平時學習認真、基礎扎實的學生，這次數學考試都能獲得高分.這些都說明我們平時的教學要注重挖掘教材，強化基礎知識和基本問題的教學，反映回到基本素材和原始狀態的教學是多么重要啊！今年重慶高考文、理科數學試題，完全符合今年重慶市考試說明與要求，且難度適中，知識點覆蓋全面，適合全體高三學生，個別試題新穎，整體層次感強，全卷有較好的區分度，是一套全面檢測和選拔人才的好試卷.

1.張曉斌.立足重慶搖促進課改——2014年高考數學重慶卷試題特點述評［J］.中學數學（上），2014（9）.

2.張曉斌.回到基本素材和原始狀態的教學才是好的教學——“數學歸納法（第一課時）”教學點評［J］.中國數學教育（高中版），2015（4）.