既關注數學文化，又夯實數學基礎*
——2015年湖北省高考理科數學試卷分析

☉華中師范大學數學與統計學學院 袁素群

☉華中師范大學數學與統計學學院 李志斌

☉華中師范大學數學與統計學學院 徐章韜

既關注數學文化，又夯實數學基礎*
——2015年湖北省高考理科數學試卷分析

☉華中師范大學數學與統計學學院 袁素群

☉華中師范大學數學與統計學學院 李志斌

☉華中師范大學數學與統計學學院 徐章韜

2015年湖北高考數學卷的命制，貫徹了《考試大綱》的要求，體現了“穩中求創新”的成熟設計理念.堅持對“四基”的考查.試卷結構穩定，考點分布合理，試題注意謀篇布局與中學教學內容相協調，注重試題表述方式與教材一致，為關鍵詞加點以提醒考生注意審題，具有人文關懷.

一、總體評析

今年湖北省高考理科數學卷繼承了湖北卷一貫的風格.

一方面，它以數學學科知識體系的重點內容為基礎.綜合知識點間的內在聯系，從多個角度考查了學生對中學數學知識體系的認識和理解.既落實了數學新課程標準的要求，又綜合考查學生對數學本質的理解、學生的數學素養等.如表1所示，從試卷考查的知識內容來看，主要考查代數、幾何及選做題三個部分.試卷在各知識點所賦分值與現行教材的課時安排基本保持一致.代數知識約占試卷總分數的69.4%，其中函數、三角函數、數列、概率統計等內容占的比重較大，而這些知識正是新課程標準所著重強調的.幾何部分約占27.3%，高考依然重視對解析幾何、立體幾何、向量的考查.幾何證明選講、坐標系與參數方程保持5分的分值不動，它們以選做題的形式出現，給考生提供了選擇的空間.

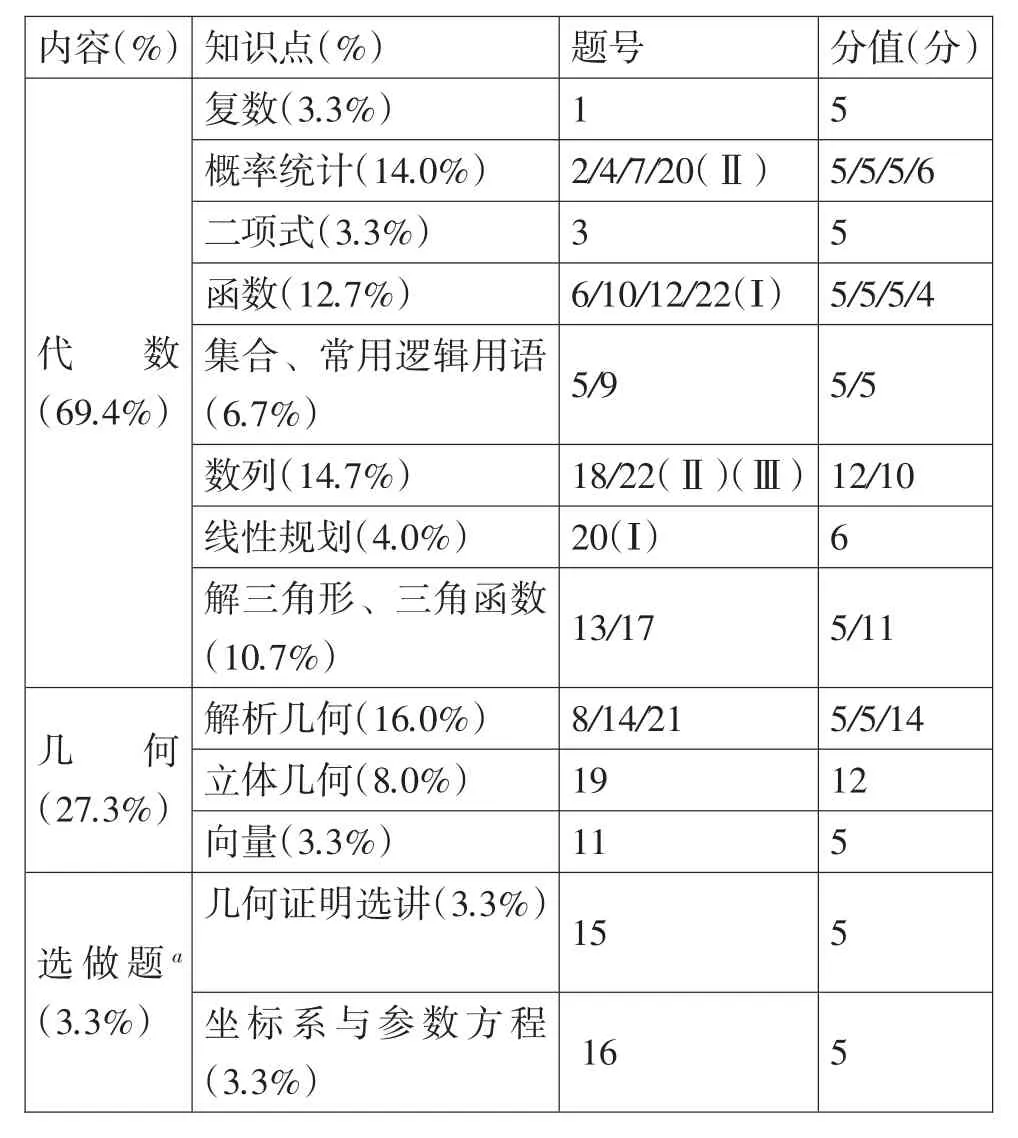
表1：知識點分布表

另一方面，綜合難題的表現形式既通俗易懂，又包含了數學知識與數學思想方法之間的交叉、綜合與滲透.如表2所示，考查學生能否綜合運用數學思想方法，做到融會貫通.同時命題專家們為部分試題挑選了合理的背景、引入數學史知識來擴展學生的知識面，有利于促進學生對我國數學文化的了解.試題能夠達到檢測學生內在數學知識結構是否完整的目的，有利于高考的選拔.

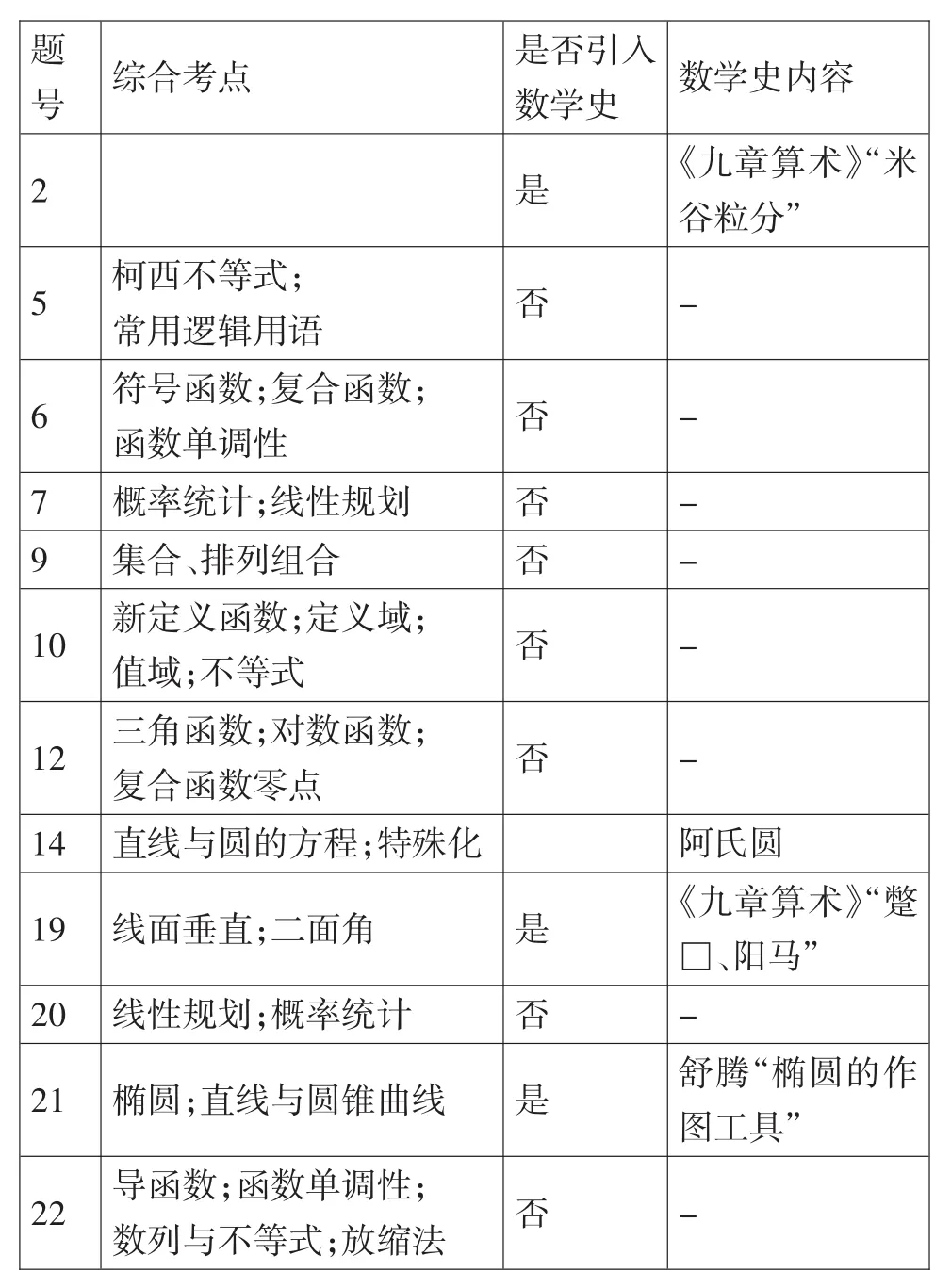
表2：綜合知識點與數學史分布表

二、試題特色

1.重視基礎，強調數學本質

縱觀歷年高考試題，有相當一部分試題對基本概念、定理、性質等基礎知識和通性、通法進行了多角度、多層次的考查.注重考查基礎知識和基本技能，檢驗考生理解數學概念本質的能力.今年也不例外，選擇題第1－4題都是直接對基礎知識進行考查的中低檔難度的試題，試題設計靈活，對基礎知識的考查呈現多角度性.分別考查了復數的基本概念、樣本估計、二項式系數和正態分布曲線.第5題考查的是等比數列、充分必條件與必要條件，根據柯西不等式、等式成立的條件，可以判斷p是q的充分條件，但不是q的必要條件.對于第8題，考生既可按雙曲線離心率的計算公式和真分數不等式進行推理，也可借助雙曲線的離心率的幾何意義解題，其間隱現著雙曲線的離心率動態變化的本質特征.

試題設計依綱靠本，定位貼近教材，呈現方式自然，主干知識突出.填空題第11題考查了平面向量的加法法則，向量垂直和向量的模與數量積.第12題考查了二倍角的正弦、余弦公式，誘導公式以及函數的零點.第13題考查了三角形內角和定理、三角函數、有關測量中的幾個術語和正弦定理.解答題第17題考查了三角函數的性質、平移、“五點法”，第18題考查了等差數列、等比數列的通項公式、用錯位相減法求數列的前n項和.這些題目分別源自教材的相關例題、習題，依據教材中的素材，經過組合加工、改造整合和拓展延伸而來.這些試題以熟悉的面孔出現，有利于考生穩定心態，正常發揮.

2.知識與能力并重

試題堅持知識立意、問題立意和能力立意并重，注重在知識交匯點設計試題.第6、9、10題，采用新定義、新概念立意設題，題型新穎別致，能有效地區分考生對數學概念的理解程度，考查考生的數學能力.第9題將新定義的集合運算與整點問題、向量平移、不等式表示的平面區域等知識巧妙地結合在一起，綜合性強，解法多樣，能較好地甄別考生的數學素養.第16題結合參數方程與極坐標考查直線與圓錐曲線的位置關系.第20題將概率統計與線性規劃有機融合，用生活中普遍存在的隨機規劃問題展現數學的應用價值.

借試題情境體驗、感悟和反思數學問題，以突出對通性、通法和數學素養的考查.這些試題把數學知識、思想方法和數學能力融會貫通，要求考生在試題所創設的情境中，有意識地應用數學知識和技能處理問題，綜合運用數學思想方法找到合理簡捷的解題途徑.

3.數學史知識的引入

（1）引入數學史，彰顯數學文化.

試題中有不少與數學史等知識有關的數學文化.數學史知識的引入使數學充滿人文氣息，使得數學知識更易于被學生接受.如在第2題中，引入九章算術中的“米谷粒分”問題實際上是簡單的抽樣統計，數學史的引入能讓學生體會到抽樣統計方法在生活中的應用.

數學史知識的引入是試題形式上的創新.如第19題，命題者用我們并不常見的幾何體（“陽馬”和“蹩□”）為背景引入.相比普通的幾何題引入更能讓學生留下深刻的印象.這兩個詞語對相當一部分老師和學生來說可能并不熟悉，但它們的出現并不影響解題.

第21題源于荷蘭數學家舒騰（F.vanSchooten）的橢圓作圖工具［1］.這樣的作圖工具相對于課本上的橢圓作圖更為古老，但是通過思考，學生容易發現數學結論的形成并不是一氣呵成的，而是在前人的基礎上一步步創新才得以發展與完善.

（2）引入數學史知識的意義.

數學史知識的引入并不多余，建構主義強調在真實而富有意義的情境中進行學習與教學.近年來的高考題所考查的內容，都盡量回避陳題，尋求新面貌、新形式.有的甚至引入高等數學知識來創設新情境.當考生遇到自己不曾接觸的問題或語詞時，也要保持積極的心態繼續往前.這有利于考查他們臨危不亂、不被困難所擊敗的精神.取材于數學史料的高考題還能幫助中學生了解我國早期在數學研究上的一些杰出的成就，讓學生體會到我國博大精深的數學文化，有利于培養民族自信心.

數學史的引入與新課標卷相互關聯.今年的湖北數學高考題作為湖北省自主命題的收官之作，它與新課標全國卷有著密切的聯系.如湖北卷理科第2題與新課標全國卷Ⅰ第6題都是取自中國古代數學名著《九章算術》.師生應克服畏難心理，回歸課標，從提高數學素養入手，提高綜合能力；有針對性地進行解題訓練；完善知識網絡，優化數學認知結構.

4.設置綜合難題，強調知識交匯

高考題大多不是基礎知識的簡單羅列或再現.高考作為選拔人才的考試，選拔性主要體現在綜合難題上.今年的湖北高考題也站在數學學科整體高度設計試題，注重知識之間的交叉、滲透、綜合，在知識網絡交匯處命題，提高了試題的難度，體現了高考的選拔作用［2］.

如選擇題第6題在符號函數的基礎上構造新函數，考查函數的單調性.選擇題第10題自定義取整函數與指數函數的復合函數，綜合考查了復合函數的定義域和值域，需要借助相關的不等式組知識求得答案.填空題第14題第二問取材于阿波羅尼斯圓.第20題將概率統計與線性規劃相結合，以線性規劃為基礎，結合分類討論的思想，將概率題的難度提高，如果學生不能很好地解決線性規劃問題，就很難繼續作答.第21題第二問考查直線與直線、直線與圓錐曲線之間的位置關系，還考查了學生能否靈活運用分類討論的思想方法，有效地結合方程思想解題.特別是壓軸題第22題，將函數、導數、數列、數學歸納法、均值不等式、不等式證明和合情推理等融于一爐，構思獨特而富有韻味，能夠考查考生的數學思維能力、數學經驗和學習潛能.

三、總結與建議

1.夯實基礎，抓住數學本質

萬變不離其宗，數學基礎知識是數學的根基，沒有這個根基，數學思維和能力的生成與發展就猶如無本之木，不會有長遠的發展.教材是高考試題的重要來源，它包含了重要知識、思想和方法.為了夯實學生的數學基礎，我們應回歸教材，以不變應萬變.教師應抓住數學概念的內涵與外延，抓住數學概念的本質進行教學.注重采用變式教學，強調抽象與具體的統一，注重數學概念思維的發展.不能讓學生陷入紛繁復雜的題海戰術之中.

2.在教學中滲透數學思想方法

數學思想方法是數學知識體系的靈魂，它是解題的指南針［3］.隨著“課程標準”取代“教學大綱”，數學思想方法得到了更加廣泛的重視，數學思想方法成為現代數學教育的重要目標.掌握數學思想方法有助于提高數學學習的效率，形成良好的數學認知結構.教師在平時的教學中，應深入鉆研教材，充分挖掘其中的思想方法，將數學思想方法滲透到教學中去.

3.提升教師自身的數學素養

“站得更高，所以看得更遠”，數學教學也是如此，新時代背景下的數學教師，要跟上時代的步伐，提高自身的數學素養.如將信息技術與數學教學有機結合起來.幾何畫板、超級畫板等新型教育技術軟件的出現，有利于幫助教師形象地展示數學知識的產生與發展.

教師要關注數學教育研究領域最新、最前沿的研究成果.如在文4中介紹了塹堵（兩底面是直角三角形的正柱體）、陽馬（直角四棱錐體）、蹩□（四個面都是勾股形的四面體）的由來和性質.在文5中詳細介紹了用符號函數表示函數的單調性、刻畫絕對值等應用.符號函數作為一種特殊的數學記號是我們探索數學問題的有用工具.關注專業期刊雜志能幫助教師了解數學發展的方向，提升數學教師的專業水平的同時提高教師的數學素養.

1.吳俊，汪曉勤.數學史融入數學教學的實踐：他山之石［J］.數學通報，2014，52（2）.

2.劉春林.如何巧妙化解數學高考的難點：以2010年江蘇省高考數學試卷為例［J］.教學與管理，2011（3）.

3.胡典順，徐漢文.突出數學本質，彰顯課程理念：對2009年高考數學湖北卷的評析［J］.數學通報，2009，48（11）.

4.徐章韜，王春華.為什么圓錐體積是等底等高圓柱體積的［J］.湖南教育（下），2010（9）.

5.裴光亞.符號函數的應用［J］.中學數學，1996（1）.

*本文系華中師范大學研究生教學研究項目“數學教育方向研究生學術水平提升的研究”的部分戰果.