剪不斷理還亂的條件概率
——引例梳理條件概率思維

☉江蘇省口岸中學 高國圣

剪不斷理還亂的條件概率
——引例梳理條件概率思維

☉江蘇省口岸中學 高國圣

引例：一個家庭中有兩個小孩，假定生男生女是等可能的，已知這個家庭有一個是女孩，問：這時另一個孩子是男孩的概率是多少？

條件概率指的是在事件A發生的條件下，事件B發生的概率.教師在講解此題時，學生普遍認為答案是究其原因是沒有理解條件概率的內涵，因此可讓學生回答如下三個問題.

問題1：一個家庭中有兩個小孩，可能有幾種情況？

答：（男，男）（男，女）（女，男）（女，女）.

問題2：其中一個是女孩，有幾種情況？

答：（男，女）（女，男）（女，女）.

問題3：在其中一個是女孩的條件下，另一個是男孩的概率？

至此問題不攻自破.

對于條件概率的理解，筆者結合自己的教學經驗，建議從如下幾方面入手，供參考.

一、借助圖示法理解條件概率的本質

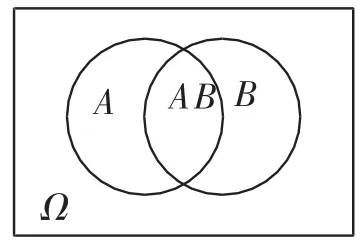
圖1

如圖1，設A、B是兩個事件，且P（A）＞0，在事件A已發生的條件下，事件B發生的概率稱為條件概率，記作P（B|A）．從圖示法的角度來看，這個定義可以理解為：

事件的樣本點已落在圖形A中（事件A已發生），問落在B中（事件B發生）的概率．由于樣本點已經落在A中，且又要求落在B中，故只能落在AB中．在這種觀點下，原來的的樣本空間Ω（即基本事件的范圍）變為已知的條件事件A所對應的空間，原來的事件B對應的空間變為事件AB對應的空間．因此，條件概率問題可以看成“樣本空間減少”的條件下的古典概型或幾何概型問題．

例1（2011年高考遼寧卷）從1、2、3、4、5中任取2個不同的數，事件A＝“取到的2個數之和為偶數”，事件B＝“取到的2個數均為偶數”，則P（B|A）＝（）.

評析：在“減少樣本空間”的觀點下，條件概率P（B|A）的計算公式為其中，在古典概型中，n（A）與n（AB）分別表示事件A與事件AB所包含的基本事件的個數.

二、弄清P（B|A）與P（AB）的區別

P（AB）與P（B|A）是兩個截然不同的事件的概率，P（AB）表示事件A與B同時發生的概率，而條件概率P（B|A）表示在事件A已經發生的條件下事件B發生的概率.

例2（2015年高考陜西卷）隨機抽取一個年份，對西安市該年4月份的天氣情況進行統計，結果如下：

?

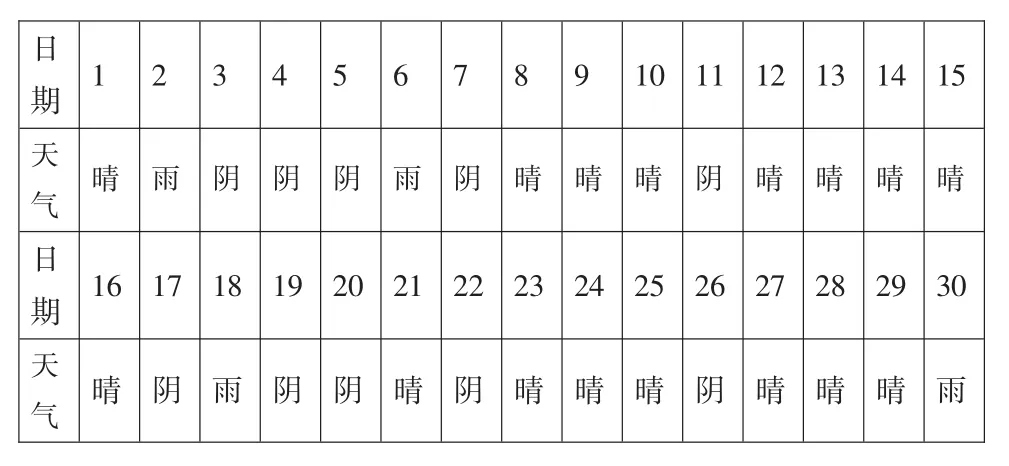
（Ⅰ）在4月份任取一天，估計西安市在該天不下雨的概率；

（ⅠⅠ）西安市某學校擬從4月份的一個晴天開始舉行連續兩天的運動會，估計運動會期間不下雨的概率.

解析：（Ⅰ）在容量為30的樣本中，從表格中得不下雨的天數是26，以頻率估計概率，從4月份任選一天，西安市不下雨的概率是

（ⅠⅠ）稱相鄰兩個日期為“互鄰日期對”（如1日與2日，2日與3日等），這樣在4月份中，前一天為晴天的互鄰日期對有16對，其中后一天不下雨的有14個，所以晴天的次日不下雨的頻率為，以頻率估計概率，運動會期間不下雨的概率為

評析：在解題中需注意P（B|A）與P（B）的關系：計算P（B）是在整個樣本空間Ω上考慮事件B發生的概率，計算P（B|A）是在A發生的范圍內來考慮事件B發生的概率.樣本空間從Ω減少為A，往往會導致無條件概率P（B）與條件概率P（B|A）并不相等.若事件A與B是相互獨立事件，則P（B）=P（B|A）.

三、幾何概型下的條件概率問題

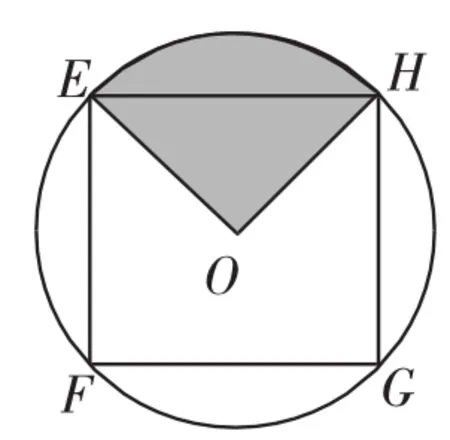
圖2

例3（2011年高考湖南卷）如圖2，EFGH是以O為圓心、半徑為1的圓的內接正方形．將一顆豆子隨機地扔到該圓內，用A表示事件“豆子落在正方形EFGH內”，B表示事件“豆子落在扇形OHE（陰影部分）內”，則（1）P（A）＝______；（2）P（B|A）＝______.

四、概率性質的應用

例4（2013年高考新課標Ⅰ卷）一批產品需要進行質量檢驗，檢驗方案是：先從這批產品中任取4件作檢驗，這4件產品中優質品的件數記為n.如果n＝3，再從這批產品中任取4件作檢驗，若都為優質品，則這批產品通過檢驗；如果n＝4，再從這批產品中任取1件作檢驗，若為優質品，則這批產品通過檢驗；其他情況下，這批產品都不能通過檢驗．假設這批產品的優質品率為50%，即取出的每件產品是優質品的概率都為且各件產品是否為優質品相互獨立．

（1）求這批產品通過檢驗的概率；

（2）已知每件產品的檢驗費用為100元，且抽取的每件產品都需要檢驗，對這批產品作質量檢驗所需的費用記為X（單位：元），求X的分布列及數學期望．

解析：（1）設第一次取出的4件產品中恰有3件優質品為事件A1，第一次取出的4件產品全是優質品為事件A2，第二次取出的4件產品都是優質品為事件B1，第二次取出的1件產品是優質品為事件B2，這批產品通過檢驗為事件A，依題意有A＝（A1B1）∪（A2B2），且A1B1與A2B2互斥，所以P（A）＝P（A1B1）＋P（A2B2）＝P（A1）P（B1|A1）＋

（2）X可能的取值為400、500、800，并且P（X＝400）＝所以X的分布列為

?

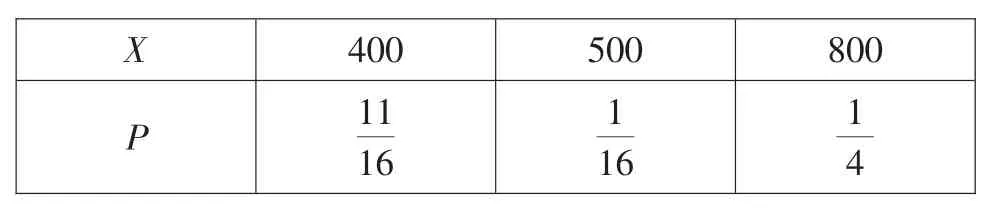
評析：若事件A發生了，事件B才有可能發生；若事件A沒有發生，事件B就不可能發生了.反過來，若事件B發生了，事件A必然發生了，即事件A、B都發生了.事件A發生是事件B發生的必要不充分條件.也就是說，“事件A發生的條件下，事件B發生”中的條件是“事件B發生”的條件.此時，P（B）=P（AB）=P（A）P（B|A）.本題是概率的綜合問題，掌握基本概念及條件概率的基本運算是解決問題的關鍵.

總之，條件概率有著較廣泛的應用，而且對于進一步加深對概率問題的理解和學習概率也有著實際意義.如何把握好難度，使學生正確地理解條件概率的概念和它的計算方法，對于加深學生對概率問題的理解和進一步學習概率都有著重要的意義.