處理高中數(shù)學最值問題的方法探析

處理高中數(shù)學最值問題的方法探析

☉江蘇省南通市通州區(qū)劉橋中學周永忠

數(shù)學是一門工具型學科，高中數(shù)學教學內(nèi)容抽象難懂給不少學生帶來了困難，特別是高中數(shù)學中最值問題的處理一直困擾著學生.最值問題是高中數(shù)學課程教學的重點和難點之一，涉及的范圍較廣，可以說分布在高中數(shù)學各個知識點與知識層面中，在最值問題中，不僅考查了化歸思想、數(shù)形結(jié)合和分類討論等各種方法，而且考查了學生的創(chuàng)新能力與邏輯思維能力，因此，探討高中數(shù)學最值問題的解題方法，對提高高中數(shù)學教學效率與質(zhì)量有著積極意義.本文筆者根據(jù)自身教學實踐，從四個角度分析探討處理高中數(shù)學最值問題的有效方法與手段，希望能給讀者帶來一定的幫助.

一、合理構(gòu)建高中數(shù)學函數(shù)模型，巧借函數(shù)思想處理最值問題

函數(shù)是高中數(shù)學課程教學的主要內(nèi)容之一，函數(shù)與其他知識點的聯(lián)系也比較緊密，在求解最值方面也不例外.高中數(shù)學教師在指導學生解此類題型時，應引導學生善于建立函數(shù)模型，利用函數(shù)思想求解最值.

例1已知a為實數(shù)，函數(shù)f（x）=x2+|x-a|+1，求函數(shù)f（x）的最小值.

思路分析：由題目中的已知條件可知：題目中既含有未知參數(shù)a，又含有絕對值，解題的關(guān)鍵是對未知參數(shù)a的取值范圍進行討論，去掉絕對值，從而簡化題目，找到正確的解題思路.

解析：（1）當x≤a時，f（x）=x2-x+a+1

（2）當x≥a時，函數(shù)f（x）=x2+x-a+1

點評：本題考查函數(shù)、絕對值、單調(diào)性等知識的綜合應用，合理運用分類討論思想指導解題過程，針對原題等價轉(zhuǎn)化成學生熟悉的形式進行處理，提高了解題的成功率，體現(xiàn)了函數(shù)模型處理極值問題的優(yōu)越性.

二、根據(jù)實際情況靈活變換數(shù)學公式，借助于函數(shù)的有界性處理最值問題

高中數(shù)學內(nèi)容涉及很多的公式，尤其是三角函數(shù)公式非常多，使得學生在三角函數(shù)求最值的題型中感覺無從下手，所以高中數(shù)學教師需要幫助學生靈活運用公式，通過公式變換，利用函數(shù)的有界性求解最值.

例2已知函數(shù)f（x）=sin2x+2sinxcosx+3cos2x，x∈R，求函數(shù)f（x）的最大值及取得最大值時自變量x的集合.

思路分析：三角函數(shù)求最值的基本思路是將函數(shù)形式通過公式變換，轉(zhuǎn)化為f（x）=Asin（ωx+φ）+b的形式，再依據(jù)具體條件求出最值.

解析：f（x）=sin2x+2sinxcosx+3cos2x

點評：本題主要涉及三角函數(shù)的性質(zhì)、三角函數(shù)公式變換、已知三角函數(shù)值求角度等知識，著重考查學生對三角函數(shù)知識的綜合運用能力.解題的關(guān)鍵是利用公式變換，簡化函數(shù)形式，再利用函數(shù)的有界性求解最值.

三、借“遷移理論”促新、舊知識之間的有效遷移，高效處理高中數(shù)學最值問題

學習遷移理論有效滲透到課堂教學之中，能夠有效促進學生“舉一反三、觸類旁通”能力的提升與發(fā)展.由于高中數(shù)學不同知識點之間存在千絲萬縷的聯(lián)系，因此在學生求解最值而毫無思路時，教師可以指導學生將知識進行合理、有效遷移，利用學生已經(jīng)掌握的數(shù)學知識與規(guī)律去處理最值問題，使學生在處理數(shù)學難題的過程中做到“游刃有余”.

例3設(shè)等差數(shù)列{an}的前n項和為Sn，已知S4≥10，S5≤15，試求a4的最大值.

思路分析：在審查題目后，很多學生首先想到的是利用數(shù)列知識，將題目中S4和S5利用前n項和公式展開再進行求解，這樣不僅計算過程煩瑣，而且容易出現(xiàn)錯誤.如果學生注重數(shù)學知識的遷移，將數(shù)列知識轉(zhuǎn)化為線性規(guī)劃問題，則可以簡化計算過程，快速解題.

解析：根據(jù)題意可將原題有效轉(zhuǎn)化為線性規(guī)劃問題：其約束條件為2a1+3d≥5和a1+2d≤3，目標函數(shù)為a4= a1+3d；建立直角坐標系a1Od，畫出其可行區(qū)域（如圖1），可知：當a4=a1+3d過可行區(qū)域內(nèi)點（1，1）時，截距最大，此時目標函數(shù)可以取最大值，即a4=4.

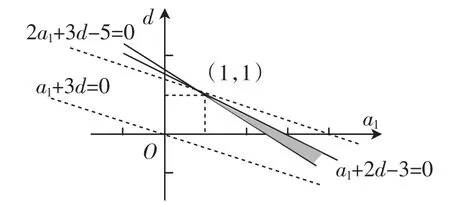
圖1

點評：數(shù)列是高中數(shù)學較難的知識點之一，很多學生在利用數(shù)列知識解題時總感覺力不從心，無法找到正確的思路與方法，而線性規(guī)劃則較為簡單，學生掌握程度較高，在求解最值時將數(shù)列問題轉(zhuǎn)化為學生熟悉的線性規(guī)劃問題，可以幫助學生順利求解出最終答案.

四、充分發(fā)揮“數(shù)形結(jié)合”思想的優(yōu)越性，巧妙處理高中數(shù)學最值問題

在處理最值問題時，數(shù)學教師完全可以根據(jù)實際情況，指導學生靈活運用數(shù)形結(jié)合的思想方法，通過形象直觀的觀察分析，簡化題目條件，找到正確的解題思路與方法.例4已知對一切x>0恒成立，求a的最大值.

思路分析：如果學生采用常規(guī)思路，按照分類思想去絕對值求解，則很容易陷入分類過多的泥沼，無法迅速求解出答案.利用數(shù)形結(jié)合思想，將題目已知條件轉(zhuǎn)化為圖形，則學生的思路會豁然開朗.

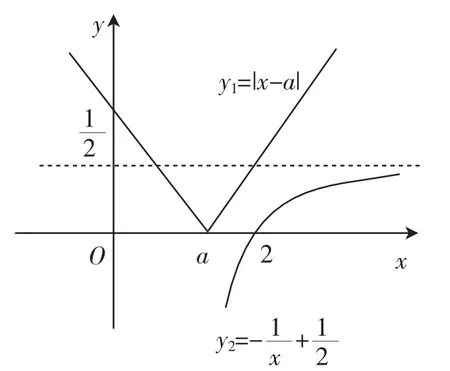
圖2

點評：本題中利用數(shù)形結(jié)合的數(shù)學思想方法，避開了絕對值、反比例函數(shù)和未知參數(shù)a對學生思路的影響，讓學生通過觀察圖形找到求解最值的方法，既提高了學生解題的成功率，又縮短了學生解題的時間.

總而言之，最值問題是高中數(shù)學教學的重點和難點，對學生綜合應用數(shù)學知識與規(guī)律非常重要.在課堂教學中，高中數(shù)學教師不但需要幫助學生掌握基礎(chǔ)的數(shù)學知識，而且需要幫助學生掌握求解最值的各種方法，讓學生可以通過知識的觸類旁通，拓寬學生的解題思路，從而實現(xiàn)提升學生分析能力和解題能力的目的.A