基于Davenport風速譜的火箭及其發射平臺風致響應分析*

蔣國慶，李道奎(國防科技大學航天科學與工程學院，湖南長沙410073)

基于Davenport風速譜的火箭及其發射平臺風致響應分析*

蔣國慶，李道奎
(國防科技大學航天科學與工程學院，湖南長沙410073)

基于Davenport風速譜，采用M.Shinozuka法計算得到了三種不同基本風速下火箭芯級和助推器不同站點的風荷載時程樣本，并調用MSC.Nastran軟件對火箭及發射平臺進行了瞬態響應分析，得到了停靠時不同基本風速下火箭及發射平臺的位移響應。隨著高度的增加，火箭芯級上各點的位移響應隨之增加；不同基本風速下同一節點的最大位移之比約等于不同基本風速的平方之比。同時在臍帶塔上設計了一個橫拉減載結構，相同基本風速下的火箭位移響應明顯減小，火箭及發射平臺的抗風能力得到提高，對工程實際有較大的參考價值。

有限元法；風致響應；減載結構

隨著人們對火箭運載能力的提高，火箭的尺寸越來越大，部分火箭的高度甚至超過了60m。如此高的火箭在轉運或者發射時會有較長時間暴露在近地風中，尤其在海島等近地風比較大的地方，相對較柔的箭體可能會發生比較大的擺動，這可能導致箭體與擺桿發生碰撞。因此需要對風荷載作用下的火箭位移響應進行計算，并根據計算結果采取相應措施。

近地風具有明顯的紊亂性和隨機性［1］。高聳結構在近地風作用下，可能產生順風向、橫風向和扭轉效應［2］，而其風致響應主要是由順風向湍流引起的［3］。徐旭等［4］通過對比分析采用石沅臺風風譜、田浦臺風風譜和Davenport風譜［5］計算該結構風載時程及風振響應結果的差異性，得出一些有參考價值的結論。樓文娟等［6］以沿海地區某四回路角鋼輸電塔為原型建立了有限元模型，采用諧波疊加法生成了B類風場與臺風風場下的風速時程，并在時域內對輸電塔進行了風振響應和風振系數的數值分析，同時將實驗結果與理論計算結果進行了對比分析，驗證了數值分析的有效性。本文基于Davenport風速譜，引用M.Shinozuka［7］法計算得到了火箭芯級和助推器不同節點處的脈動風荷載時程曲線，并調用MSC.Nastran軟件計算得到了三種基本風速下箭體的位移響應，同時設計一種橫拉減載結構，顯著減小了火箭的位移響應，為火箭抗風結構的設計提供了一定參考。

1 有限元建模及模態分析

火箭及其發射平臺的有限元模型如圖1所示，它主要由臍帶塔、擺桿、火箭以及發射臺組成。采用殼單元模擬臍帶塔和發射臺的框架，而其加筋結構則采用梁單元進行模擬。火箭箭體采用梁單元進行建模，推進劑采用耦合質量單元進行模擬，這樣可以準確地模擬火箭運動時推進劑對箭體橫向和對貯箱下橢球底的作用。火箭箭體通過四個支撐座與發射臺相連。各級擺桿采用桿單元進行建模，其末端圓弧與火箭外輪廓有0.5m的距離，發射臺與臍帶塔、各級擺桿與臍帶塔均通過多點約束單元RBE2進行連接。

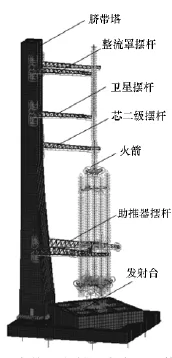
圖1 火箭及發射平臺有限元模型Fig.1 Finite elementmodel of rocket and its launching platform

為便于后續進行風荷載時程響應分析，需要對火箭及發射平臺進行模態分析。火箭及發射平臺處于停靠狀態，此時發射臺下端8個支腿為固支。模型前四階模態及相應自振頻率如表1所示。

由表1可知，火箭及發射平臺有限元模型的前四階模態中，均以火箭振動為主，而其他部分幾乎沒有振動。

2 近地風荷載的模擬

根據風的周期，可將其分成平均風和脈動風。其中平均風是持續時間大于10min的長周期風，而脈動風的周期很短，通常只有幾秒。根據中國荷載規范［8］，z高度處垂直于結構表面的平均風壓的計算公式為

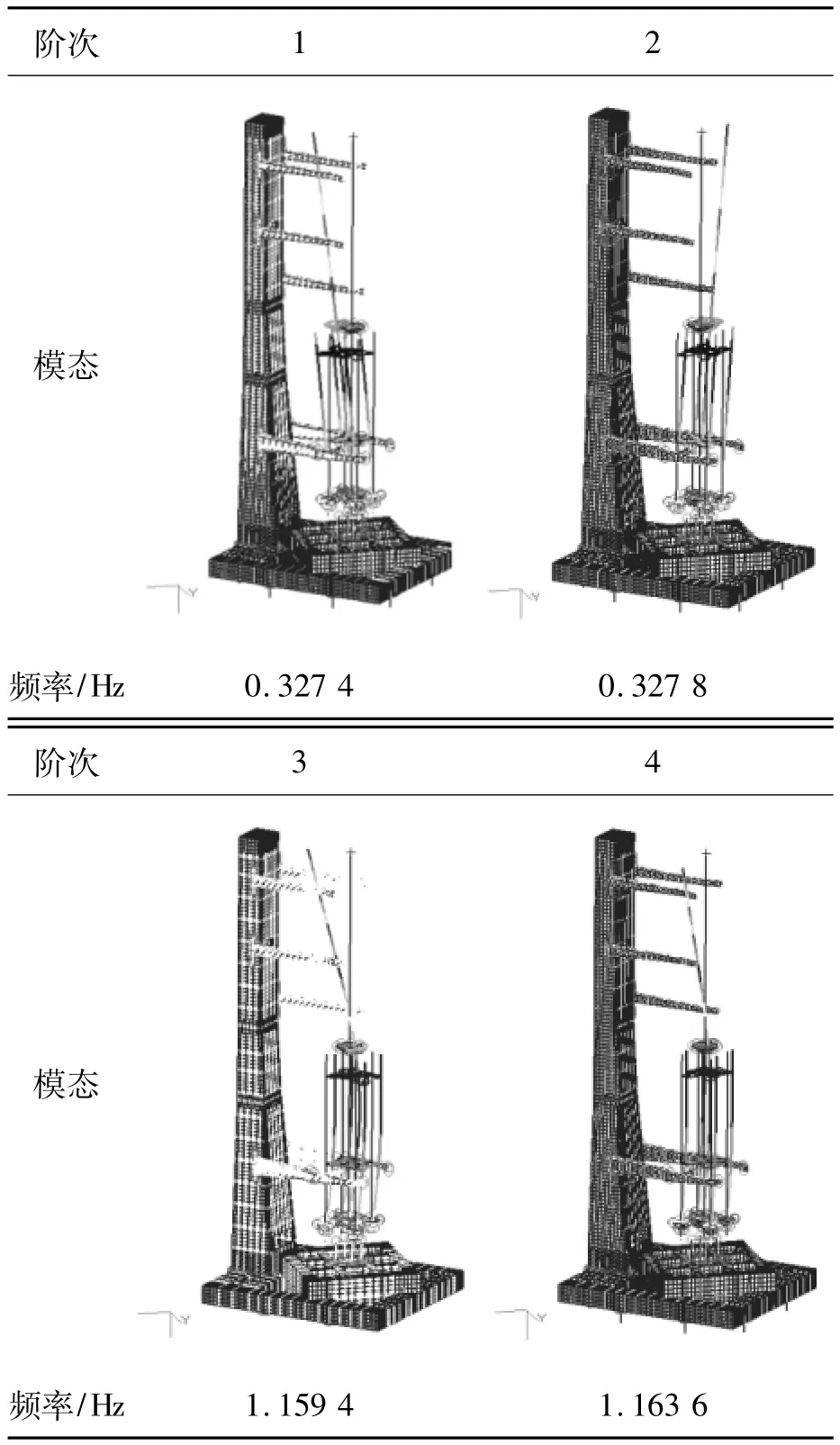
表1 火箭及發射平臺前四階模態及自振頻率Tab.1 The first four vibration modes and natural frequency of the rocket and its launching platform

式中，μr為重現期調整系數，μs為風荷載體型系數，μz為風壓高度變化系數，w0為基本風壓。計算過程中，μr，μs和μz均按照《高聳結構設計規范》［9］進行選取。w0與基本風速ˉv0有關，ˉv0為當地比較空曠平坦地面、離地10m高、統計50年一遇的10min平均最大風速［9］，本次分析了三種基本風速，分別為8m/s，10m/s，13m/s。

脈動風實際是三維的風湍流，主要包括順風向、橫風向和垂直向的湍流［10］。在此只分析火箭及發射平臺由順風向風荷載引起的響應。目前國內外使用最多的是加拿大科學家Davenport經過多次測量得到的脈動風速譜——Davenport風速譜，其功率譜密度函數為

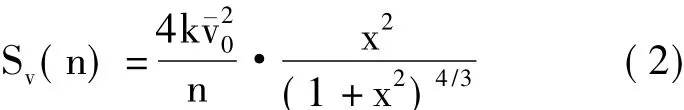
式中:x=1200n/ˉv0；k為反映地面粗糙度的系數，根據《高聳結構設計規范》取值；n為脈動風頻率，單位Hz。

Davenport風速譜是定義在頻域內的，對火箭及發射平臺的風致響應分析需要以Davenport風速譜為基礎，在時域內對脈動風荷載進行模擬。文獻［11］表明諧波合成法中的M.Shinozuka法模擬精度較高，因此本文采用此方法模擬脈動風荷載。由模態分析結果可知，臍帶塔、發射臺剛度很大，同時各級擺桿迎風面積很小，其所受風荷載相對火箭所受的風荷載而言可以忽略不計。為便于后續計算結果提取，建立如圖2所示局部右手坐標系。圖2中，火箭的迎風部件為芯級和前兩個助推器，后兩個助推器背風，暫不考慮其所受風荷載，同時暫不考慮火箭芯級與助推器、助推器與助推器、臍帶塔與火箭等相互之間對風湍流的影響。火箭芯級共113個站點，助推器共53個站點，芯級和助推器所受的風荷載需分別計算。根據M.Shinozuka法的計算公式，采用MATLAB編程計算可以得到三種風速下各個站點所受的脈動風荷載，以芯級Node1(即火箭頂端站點)為例，基本風速為8m/s時其脈動風荷載時程曲線如圖3所示。

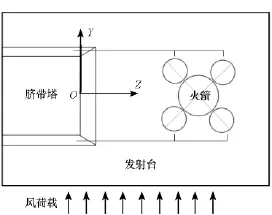
圖2 火箭及發射平臺受風示意圖Fig.2 The schematic diagram of the wind load blowing to the rocket and its launching platform

3 順風向風振響應分析

對于火箭及發射平臺這種大規模模型而言，采用解析的方法求解其動力響應不僅煩瑣，而且效率低下，而用數值方法中的有限元法得到的動力響應不僅效率高，計算結果也更可靠。因此采用MSC.Nastran軟件對火箭順風向風致響應進行分析。發射平臺底端8個支腿設置為固支，同時把不同基本風速下計算得到的芯級和助推器的風荷載時程曲線分別導入到MSC.Patran軟件中，并加載到相應站點上。同時，需要把各個站點受到的平均風荷載加到站點上。設置完畢后，調用MSC.Nastran軟件對不同基本風速下的火箭及發射平臺有限元模型分別進行計算。計算完畢后，通過MSC.Patran軟件的后處理程序對計算結果進行處理。

各級擺桿上裝有大量電纜以及其他設備，工程設計人員關心的是箭體在風荷載作用下會不會與擺桿發生碰撞。各級擺桿末端圓弧與火箭外輪廓之間的初始距離為0.5m，如果箭體擺動的幅度大于0.5m，即發生碰撞，擺桿等則需要重新設計。為便于后文的撰寫，現把各級擺桿末端所對應的芯級節點編號統計如表2所示。

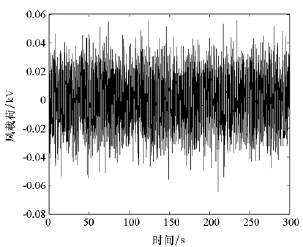
圖3 基本風速為8m/s時Node1風荷載曲線Fig.3 Wind load curve of Node 1 whenthe basic speed is 8m/s

表2 各擺桿末端所對應的芯級節點編號統計表Tab.2 Node numbers of the rocketwhich are close to the end of oscillating bars

基本風速為8m/s時，整流罩擺桿末端節點(Node16)的Y向位移(模型各節點的Y向位移均遠大于其他兩向，以下均只給出Y向位移)如圖4所示。由圖4可知，擺桿的位移可忽略不計，因此下面在計算擺桿圓弧與箭體外輪廓之間的距離時不再考慮擺桿的位移。圖5為各級擺桿末端所對應的芯級節點的Y向位移曲線，各節點的最大位移統計如表3所示，其中Dmax為各節點Y向最大位移。

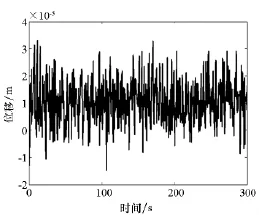
圖4 基本風速為8m/s時Node16的Y向位移曲線Fig.4 Displacement curve at Y direction of Node16 when the basic wind velocity is 8m/s

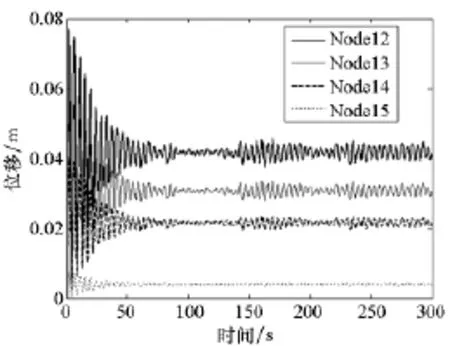
圖5 基本風速為8m/s時各點Y向位移曲線Fig.5 Displacement curve at Y direction of each node when the basic wind velocity is 8m/s

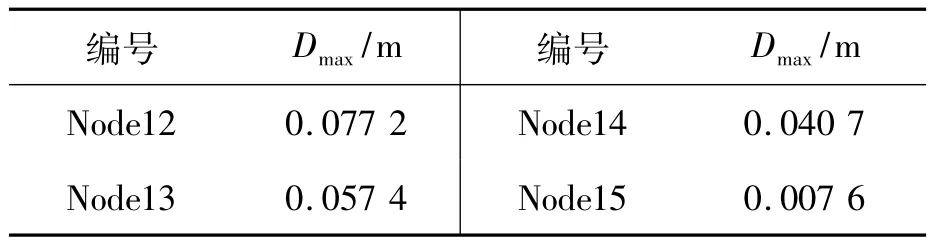
表3 基本風速為8m/s時各節點Y向最大位移Tab.3 Maximal displacement at Y direction of each node when the basic wind velocity is 8m/s

由表3可知，芯級上四個節點中，離地高度越大的節點其位移越大，相應的各節點與擺桿之間的距離也就越小，但這四個位置的擺桿與火箭均不會發生碰撞。對于不同的基本風速，在此只給出Node12的Y向位移曲線，如圖6所示。

對圖6進行統計，可以得到不同基本風速下Node12的最大位移、平均位移，如表4所示，其中Dave為Y向平均位移。

由圖6和表4可知，不同基本風速下Node12的位移曲線形狀基本相同，均表現為不同時刻的位移在平均位移處上下浮動，且除開始階段浮動幅度比較大外，其余時刻浮動幅度都比較小。這說明在火箭的風振位移響應中，平均風產生了平均位移，脈動風產生了位移的脈動部分。初始時刻突然加在火箭上的平均風在過渡階段產生了比較大的位移浮動，隨著時間的推移平均風產生的位移進入穩態階段，此時平均風產生的位移即為平均位移。脈動風為各態歷經的隨機過程，它所產生的位移均值為0m。經過計算，可得132/102=1.69，0.201 7/0.118 5=1.702 1；102/ 82=1.562 5，0.118 5/0.077 2=1.535 0。由前面計算結果可得到如下式子

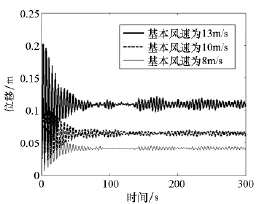
圖6 三種基本風速下Node12的Y向位移曲線Fig.6 Displacement curves at Y direction of Node12 under three basic wind velocities

表4 三種基本風速下Node12的Y向位移統計表Tab.4 Displacement statistic at Y direction of Node12 under three basic wind velocities

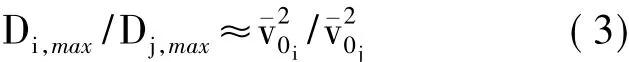
式中:ˉv0i，ˉv0j為不同基本風速；Di，max，Dj，max為不同基本風速下火箭上相同節點產生的最大Y向位移。由式(3)可知，隨著基本風速的增加，火箭各節點的最大位移也隨之增大，例如當基本風速為20m/s時，Node12的最大Y向位移為0.474m。雖然此時擺桿末端圓弧與火箭外輪廓之間的距離依然小于0.5m，但箭體內部分設備會受到一定影響，因此當基本風速較大時需要采取減載措施，減小箭體的位移響應。

4 橫拉減載結構設計

在設計橫拉減載結構時，需要考慮如下兩點:①由于減載結構安裝在臍帶塔上，因此不能太重，其對減載結構與臍帶塔連接處所產生的力不能超過連接處的承受能力；②其必須具有收縮功能，當火箭發射時能自然放下。根據實際情況，設計出如圖7所示的減載結構，該結構工作時收縮裝置處于鎖死狀態，故在此沒有給出收縮裝置示意圖。

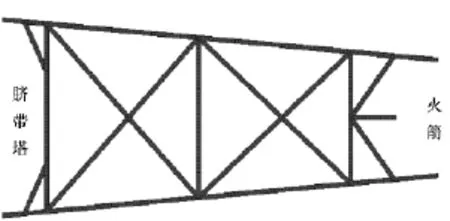
圖7 橫拉減載結構Fig.7 Load-reliving structure

設計好減載結構后，需要考慮其安裝位置，此時需要考慮如下幾點:①安裝位置不能離地太高，否則會增加安裝難度；②安裝位置不能離地太低，否則減載效果不明顯；③工作范圍內不能與臍帶塔上現有的各級擺桿產生干涉，也不能與火箭任何部位產生干涉。綜合考慮以上3點，把橫拉減載結構安裝在芯二級燃箱上。由于之前火箭的有限元模型采用的是梁單元進行建模，為便于減載結構與火箭芯級連接，需要對部分芯二級燃箱重新建模，如圖8所示。該部分芯二級燃箱采用殼單元建模，并采用RBE2單元與上下部段連接，其質量為原站點質量，其上所受的載荷等效至鄰近的站點上。

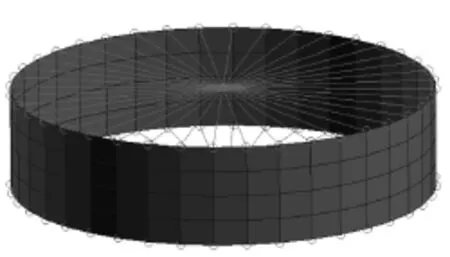
圖8 部分芯二級燃箱三維有限元模型Fig.8 Three-dimension finite elementmodel of part of the rocketwhere the fuel container is placed

考慮到基本風速為13m/s時火箭頂端的位移響應比較大，在此計算一下此基本風速下減載結構的減載效果。設置完畢后，調用MSC.Nastran進行瞬態響應分析。隨后提取Node12的計算結果與無減載結構時該節點的計算結果進行比較，如圖9所示。對圖9中重要結果統計如表5所示。

由表5可知，臍帶塔上裝有減載結構后，Node12的Y向最大位移減小了57%，說明設計的橫拉減載結構是有明顯效果的。

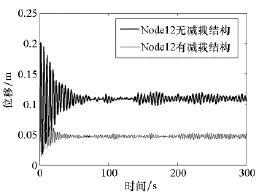
圖9 有無減載結構時Node12 Y向位移曲線Fig.9 Displacement statistic curve at Y direction of Node12 with or without load-reliving structure

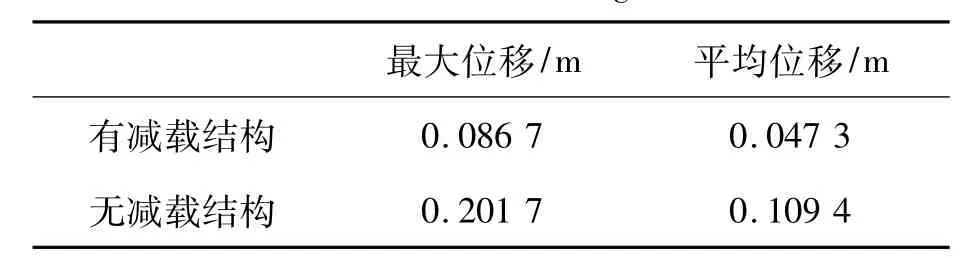
表5 有無減載結構時Node12 Y向位移統計表Tab.5 Displacement statistic at Y direction of Node12 with or without load-reliving structure

5 結論

建立了一套基于Davenport風速譜的火箭及其發射平臺風致響應分析方法和減載結構設計方法，首先基于Davenport風速譜采用M.Shinozuka法計算得到不同基本風速下火箭芯級和助推器各站點上的風荷載時程曲線，最后利用商用軟件進行瞬態響應分析，得到如下結論:

1)當基本風速為8m/s，10m/s，13m/s時，臍帶塔上各級擺桿末端圓弧均不會與火箭芯級或者助推器發生碰撞，但隨著基本風速的增大，兩者之間的距離隨之減小。

2)本文設計的橫拉減載結構能顯著減小火箭頂端的位移響應，在一定程度上能保證設備的正常工作，這能為工程實際提供一定參考。

References)

［1］張志強.合肥電視塔風振及地震響應的振動控制研究［D］.南京:東南大學，2003.ZHANG Zhiqiang.Studies of wind-induced and seismic vibration control of Hefei TV tower［D］.Nanjing:Southeast University，2003.(in Chinese)

［2］王世村.高聳結構風振響應和風振疲勞研究［D］.杭州:浙江大學，2005.WANG Shicun.Studies of wind-induced vibration and windinduced fatigue on high-rise structures［D］.Hangzhou: Zhejiang University，2005.(in Chinese)

［3］徐旭，楊方勤，屈應輝.結構橫風向非平穩隨機振動的矩分析［J］.非線性動力學學報，2004，11(12):19-30.XU Xu，YANG Fangqin，QU Yinghui.Moment analysis of nonstationary random vibration of flexible structure in crosswind direction［J］.Journal of Nonlinear Dynamics in Science and Technology，2004，11(12):19-30.(in Chinese)

［4］徐旭，劉玉.高聳結構在臺風作用下的動力響應分析［J］.建筑結構，2009，39(6):105-109.XU Xu，LIU Yu.Dynamic response analysis of a high-rising structure under typhoon［J］.Journal of Building Structure，2009，39(6):105-109.(in Chinese)

［5］Davenport A G.The spectrum of horizontal gustiness near the ground in high winds［J］.Quarterly Journal of the Royal Meteorological Society，1961，8(7):194-211.

［6］樓文娟，夏亮，蔣瑩，等.B類風場與臺風風場下輸電塔的風振響應和風振系數［J］.振動與沖擊，2013，32(6): 13-17.LOU Wenjuan，XIA Liang，JIANG Ying，et al.Windinduced response and wind load factor of transmission tower under terrain Bwind field and typhoon wind field［J］.Journal of Vibration and Shock，2013，32(6):13-17.(in Chinese)

［7］Shinozuka M，Jan C M.Digital simulation of random processes and its applications［J］.Sound and Vibration，1972，25(1):111-128.

［8］黃本才.結構抗風分析原理及應用［M］.上海:同濟大學出版社，2001.HUANG Bencai.The principle and application of structural wind resistance analysis［M］.Shanghai:Tongji University Press，2001.(in Chinese)

［9］GB50153-2006.高聳結構設計規范［S］.北京:中國計劃出版社，2007.GB50153-2006.Code for design of high-rising structures［S］.Beijing:China Planning Press，2007(in Chinese)

［10］瞿偉廉，王墨耕.高層建筑高聳結構的風振控制和設計［M］.武漢:武漢測繪科技大學出版社，1991.QU Weilian，WANG Mogeng.Wind vibration control and design of high-rising building and structure［M］.Wuhan: Wuhan Technical University of Surveying and Mapping Press，1991.(in Chinese)

［11］張志強，李愛群，蔡丹繹，等.合肥電視塔人造脈動風荷載的仿真計算［J］.東南大學學報(自然科學版)，2001，31(1):69-73.ZHANG Zhiqiang，LIAiqun，CAIDanyi，etal.Simulation of dynamic wind load on the Hefei television tower［J］.Journal of Southeast University(Natural Science Edition)，2001，31(1):69-73.(in Chinese)

W ind-induced responses of a rocket and its launching p latform based on Davenport w ind speed spectrum

JIANG Guoqing，LIDaokui
(College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China)

On the basis of Davenportwind speed spectrum and using M.Shinozukamethod，samples ofwind load were numerically simulated on the differentgirds of rocket core and booster under three basic wind velocities.Then a transient response analysiswasmade to the rocketand its launching platform by invoking the MSC.Nastran，and the displacement response of the rocketand its launching platform under differentbasic wind velocities was obtained.The value of the displacement increases along with the increase of height away from the ground，and the ratio of the maximal displacement approximates to the ratio of the square of basic wind velocity on a grid.Finally，a designed load-relieving structure was placed on the umbilical cord tower.Results indicate that themaximal displacement on different grids decreases conspicuously and the anti-wind capability of the rocket and its launching platform are enhanced by a large margin with the help of the load-relieving structure.The designed structure can make a reference to the engineering practice.

finite elementmethod；wind-induced response；load-relieving structure

V435

A

1001-2486(2015)05-104-06

10.11887/j.cn.201505016

http://journal.nudt.edu.cn

2014-12-02

國家973計劃資助項目(613277)

蔣國慶(1987—)，男，湖南新邵人，博士研究生，E-mail:jieye1987@126.com；李道奎(通信作者)，男，教授，博士，碩士生導師，E-mail:lidaokui@nudt.edu.cn