基于測力和測壓試驗的氣動導納識別結果比較

檀忠旭, 朱樂東, 3,*, 徐自然, 陳 偉, 3

(1. 同濟大學 土木工程防災國家重點實驗室, 上海 200092; 2. 同濟大學 橋梁工程系, 上海 200092; 3. 同濟大學 橋梁結構抗風技術交通行業重點實驗室, 上海 200092)

基于測力和測壓試驗的氣動導納識別結果比較

檀忠旭1, 2, 朱樂東1, 2, 3,*, 徐自然1, 2, 陳 偉1, 2, 3

(1. 同濟大學 土木工程防災國家重點實驗室, 上海 200092; 2. 同濟大學 橋梁工程系, 上海 200092; 3. 同濟大學 橋梁結構抗風技術交通行業重點實驗室, 上海 200092)

氣動導納是大跨度橋梁抖振分析的重要參數，通常通過格柵湍流場測力或測壓風洞試驗進行識別。然而，測力試驗中天平和節段模型系統的固有振動和測壓試驗中測壓管路系統的頻響效應都會對氣動導納的識別結果產生影響。本文通過格柵湍流場測力和測壓試驗、采用抖振力自譜和抖振力脈動風交叉譜綜合殘量最小二乘法識別了準平板斷面的氣動導納，其中，在基于測力試驗的氣動導納識別中考慮了模型抖振力跨向不完全相關效應的影響，在基于測壓試驗的氣動導納識別中考慮了按Bergh-Tijdeman理論公式修正或者不修正測壓管路系統頻響特性影響的2種情況。在此基礎上，通過考察氣動導納實驗識別結果之間的差別及其與平板斷面氣動導納理論解Sears函數之間的差別，研究了天平模型系統固有振動以及測壓管路系統頻響效應對識別結果的影響。結果表明：天平模型系統的共振會顯著放大氣動導納的識別結果；而由于測壓管路的固有頻率一般要顯著高于天平模型系統的固有頻率，因此，與基于測力試驗得到的氣動導納相比，基于測壓試驗所得氣動導納總體上更加合理，可用導納的折算頻率范圍更廣。此外，在一般大跨度橋梁抖振分析所關心的折算頻率范圍內，考慮測壓管路頻響特性修正后，氣動導納有一定降低。

氣動導納；風洞試驗；測力試驗；測壓試驗；測壓管路頻響特性

0 引 言

抖振是一種由于氣流中的湍流風或風速脈動成分引起的隨機強迫振動，因此處于自然風場中的橋梁不可避免地會發生抖振現象。抖振不僅會引發橋梁的局部疲勞問題，而且還會帶來行車安全等問題。目前對于橋梁的抖振分析主要采用Davenport的抖振理論[1-2]。該理論是建立在準定常理論基礎上，通過引入氣動導納函數來修正斷面周圍湍流的非定常特性和不完全相關性，因此氣動導納是抖振分析中的關鍵參數之一。氣動導納一般通過格柵湍流場節段模型測力試驗來識別[3-6]。由于天平測到的是作用在整個節段模型上的隨機氣動力，自動包含了節段模型沿跨向不同斷面上的抖振力之間的不完全相關性的影響，因此，氣動導納識別中所需要的作用在模型斷面上的抖振力不能簡單地用天平測到的總抖振力除以模型長度來計算，應該考慮模型上的抖振力沿跨向不完全相關性效應。為此，徐自然和朱樂東提出了考慮抖振力沿模型跨向不完全相關性效應的自譜-交叉譜綜合最小二乘法[7-8]進行氣動導納的識別，但需要附加同步測壓試驗來獲得抖振力的跨向相關性函數，使氣動導納識別試驗變得過于復雜。本文以準平板斷面為對象，直接利用格柵湍流場測壓試驗結果實現橋梁斷面的氣動導納識別，并將識別結果與測力試驗所得結果進行比較。其中，為了減小測壓管路信號畸變的影響，用Bergh-Tijdeman測壓管路頻響函數的理論公式[9-10]對測壓實驗數據做出修正，分析測壓管路修正對氣動導納識別產生的影響。

1 氣動導納識別

在測壓試驗中可記錄各測點的壓強時程信號，再將此表面風壓沿斷面一周進行數值積分，便可得到該斷面上的抖振力三分力的時程曲線(包括阻力FD(t)、升力FL(t)和扭矩M(t))。進一步可應用和測力法相似的識別手段進行氣動導納的識別。本文中采用綜合考慮抖振力自功率譜以及抖振力和脈動風速交叉譜偏差的自譜-交叉譜綜合最小二乘法分別識別升力、阻力和升力矩相關氣動導納[3,7-8]，即對抖振升力、抖振阻力和抖振升力矩，各自構造含有2個未知的復數氣動導納的1個自譜方程和2個交叉譜方程，然后基于這3個譜方程構造1個綜合殘量，再運用最小二乘原理求解2個未知復數氣動導納。以升力為例，升力自譜以及升力和兩個脈動風速之間的交叉譜分別為：

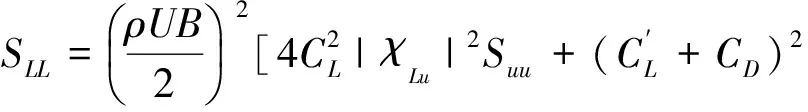
則可按下式構造綜合考慮升力自譜以及升力和2個脈動風速之間交叉譜偏差的殘量：

其中，b1,b2,b3為加權系數。

通過對式(4)所表示的加權后的殘量求最小值，則可獲得χLu、χLw這2個復氣動導納函數的實部和虛部。對阻力和升力矩可以進行類似的分析。

2 試驗模型及設備

本文中的測力試驗和測壓試驗均在同濟大學TJ-2號風洞進行，該風洞試驗段采用切角矩形截面，高2.5m，寬3.0m。準平板節段模型直接選用徐自然研究跨向相關性所采用的模型[7-8]，模型測試段長40cm，寬40cm，厚2cm，模型端部角度為2tan-1(10/60)=18.9°，近似流線型平板斷面，斷面形狀和尺寸如圖1所示。湍流場則由文水兵調試過的均勻格柵湍流裝置產生[4]，湍流度為10%，試驗風速為7.45m/s。 由于本次試驗中采用的被動格柵的擋條在豎向和水平的尺寸和間隔均一致，只是它們的長度因風洞截面為矩形而有所差異，因此由此模擬的湍流場在水平和豎向兩個方向上的湍流參數比較接近，模型豎向和水平安裝對試驗結果影響不大。有鑒于此，為了模型安裝和風迎角調節的方便，試驗中采用了豎向安裝模型的方式(見圖3)。流場的特征參數列于表1, 其中u,v,w分別表示相對于橋梁斷面的順風向、水平橫風向和豎向脈動風速分量，由于試驗中模型是豎直安裝在風洞中，因此在上述3個脈動風速分量中，除了順風向u分量對模型和風洞來說是一致的外，相對于模型的豎向脈動分量w實際為風洞中的水平橫風向脈動分量，相對于模型的水平橫向脈動分量v實際為風洞中的豎向脈動分量。

表1 試驗流場參數Table 1 Flow field parameters

圖1 準平板模型斷面

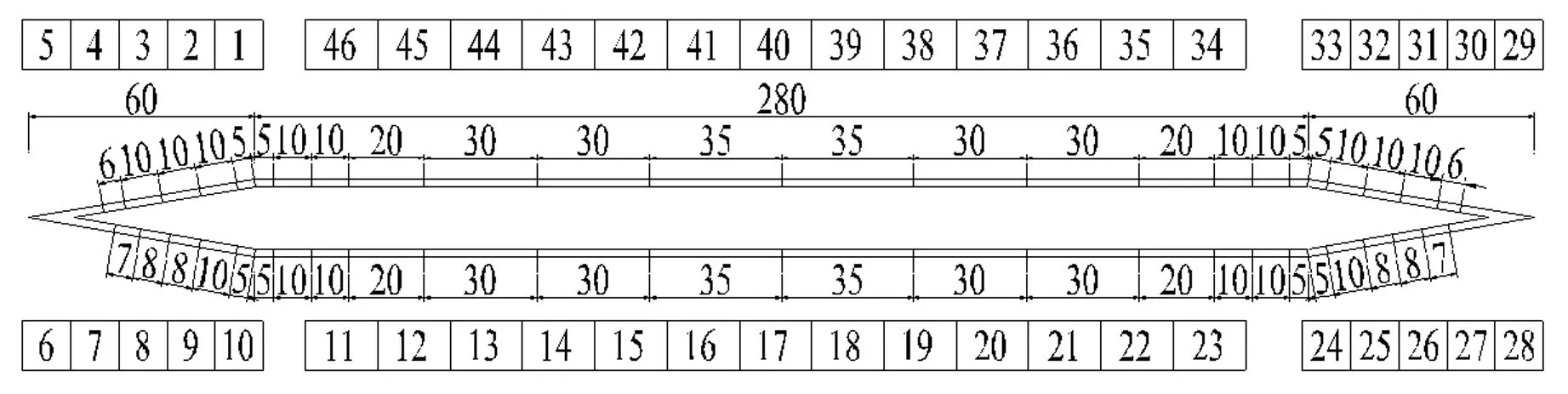
圖2 斷面測壓孔布置示意圖

在測壓模型上沿展向等間距(5cm)地布置了8個測壓斷面(見圖3)，兩端測壓面各離上下頂板2.5cm，每個測壓面布置46個測壓孔，斷面測壓孔布置如圖2所示。布置8個測壓截面的目的是為了研究模型上抖振力沿模型長度方向的相關性，但本文只討論截面上抖振力的氣動導納，只需要其中某個截面上的測壓結果。

(a) 測力試驗

(b) 測壓試驗圖3 試驗模型Fig.3 Test models

經比較分析，8個截面的風壓測量結果除了接近下部圓平臺的1#截面外均比較接近，因此，本文中的分析和討論均基于接近模型中心的5#斷面上的試驗數據。為方便計算，試驗中某一斷面上各測點所連接的測壓管長度一致，5#斷面上的測壓管長度均為85cm，內徑均為1.1cm。試驗分別采用配置了12個ESP-64HD壓力掃描閥的DTC Initium 壓力掃描系統和五分量高頻天平采集壓力信號和力信號，并采用眼鏡蛇風速探頭進行風速同步采集。風速測點在模型中心上游右側方向(如圖2所示)，離風洞地板53cm，與模型中心橫向間隔30cm，縱向間隔20cm，也即高度方向基本與5#斷面對齊，風洞縱向與模型的上游邊緣基本對齊。關于同步風速測點選取的詳細比較討論參見文獻[8]。

為減小模型端部三維流動的影響，測試段下設置水平圓盤形隔離板，上端加外形完全相同的補償段，如圖3所示。圓盤直徑1.5m，上表面離風洞地板30cm，補償的長40cm。測力試驗中，試驗段和天平組成系統的固有頻率為：豎彎22Hz、側彎49Hz、扭轉44Hz(上述試驗條件下的折算頻率K=Bω/U分別為7.42、16.53和14.84)。測壓試驗中，系統的固有頻率為：豎彎9Hz、扭轉18Hz(折算頻率分別為3.04和6.07)。

3 測壓管路頻響函數理論

有關測壓管路頻響特性分析前人已經建立起一些理論模型，本文主要利用如下所述的Bergh-Tijdeman方程[9-10]實現對脈動風壓力的管路修正。對于常見的、也是本研究中所采用的簡單段測壓管路系統，模型端脈動壓力p0和傳感器端脈動壓力p1之間的幅值比或傳遞函數公式如下：

其中：

φ

V為傳感器腔體體積；Vt為測壓管腔體體積；σ為容腔變形的無量綱系數，取0；k為多變指數，取1.4；ω為圓頻率；a0為壓力波傳遞速度(聲速)，取340 m/s；J2和J0分別為二階和零階的第一種貝塞爾函數；γ為比熱比(即絕熱指數)，取1.4；ρs為空氣密度，取1.205kg/m3；μ為流體粘性系數，取17.9×10-6Pa·s；Pr為普朗特數，取0.75。

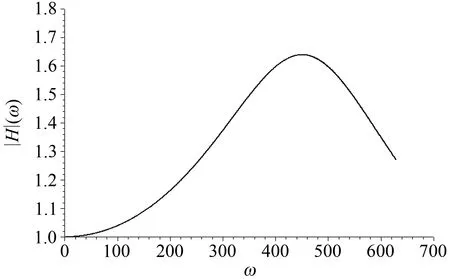
以5#斷面為例，測壓管長度為85cm、內徑均為1.1cm時得到幅值比|H|(ω)隨圓頻率ω的變化規律如圖4所示。

由于上述傳遞函數和圓頻率ω有關，因而掃描閥中測得的脈動壓力信號Y(t)首先需經由快速傅里葉變換(FFT)轉換至頻域：

(a) 幅值比

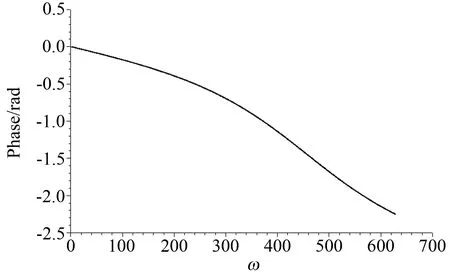
(b) 相位差圖4 Bergh-Tijdeman理論傳遞函數Fig.4 Transfer function of Bergh-Tijdeman theory

然后，再用傳遞函數對應的值對傅里葉系數Yn進行修正：

需要注意的是，在數學運算中FFT變換會使Yn在正負頻率上都有定義，但實際頻譜中只存在正頻成分，因而實際操作時只在正頻部分進行修正，再根據傅里葉系數的正頻部分和負頻部分互為共軛得到完整的Xn。

最后通過快速傅里葉逆變換(IFFT)獲得修正后的脈動壓力信號X(t)：

4 實驗結果對比

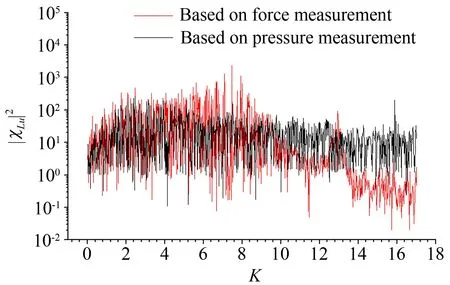
采用前文所述最小二乘方法，將測力試驗數據計算所得的氣動導納和測壓試驗數據積分后擬合得到氣動導納、以及經典的Sears函數進行對比，其中對準平板而言阻力為小量，因而不再對相應的導納進行分析，其余對比結果如圖5所示。

此外，為了明確管路效應對氣動導納擬合結果的影響，以影響較大的升力和升力矩在脈動風速w分量上的取值為例，將基于Bergh-Tijdeman方程修正前后測壓法所得氣動導納分別進行擬合，比擬Sears函數擬合公式[8]如下：

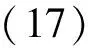
(a) 升力在u分量上的氣動導納

(b) 升力在w分量上的氣動導納

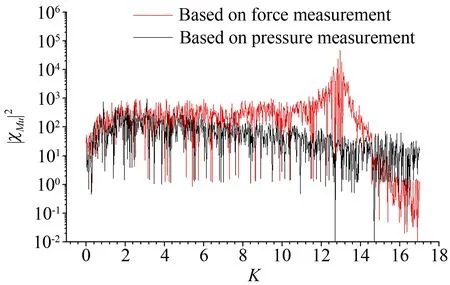
(c) 升力矩在u分量上的氣動導納

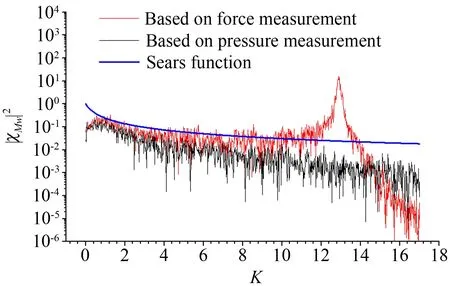
(d) 升力矩在w分量上的氣動導納圖5 測力測壓氣動導納識別結果對比Fig.5 Comparison of aerodynamic admittance recognition results

擬合后各參數取值詳見表2，擬合所得氣動導納曲線與Sears函數之間的對比如圖6所示。

(a) 升力在w分量上的氣動導納

(b) 升力矩在w分量上的氣動導納圖6 修正前后測壓法氣動導納識別結果對比

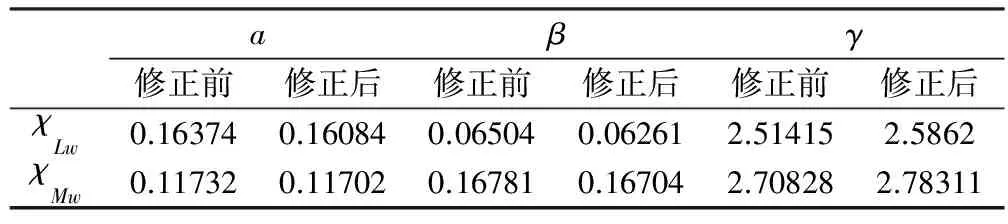
表2 擬合參數取值Table 2 Fitting parameter values

由圖5和6可見：

(1) 由測力試驗所得氣動導納在相應的模型-天平系統固有頻率上會出現峰值：升力在豎彎頻率上、升力矩則在扭轉頻率上呈現明顯峰值。由于固有頻率的限制測力法所得氣動導納往往只能應用于較低頻率范圍，相比之下，由測壓試驗所得結果并未受到系統固有頻率的影響，因此可以應用于更寬的頻域。二者產生差異的原因在于：在測力試驗中，模型微小振動會引起較大的慣性力，并傳遞到測力天平上，從而顯著地影響天平測得的抖振力；而在測壓試驗中，模型微小振動只會引起測壓點與空氣之間微小的相對運動，而由此在測壓點處產生的附加壓力是微不足道的，可以忽略。

(2) 在此次試驗條件下，關注頻率范圍以內的脈動風壓均會因管路效應而產生放大，根據圖4所示，文中準平板斷面當折算頻率低于24時放大程度會隨著頻率的增加而增大。管路修正可以在一定程度上降低此種放大效應，因此修正后的氣動導納較修正前有所減小。

(3) 對于起主要作用的脈動風速w分量相關的升力和升力矩氣動導納而言，由于避免了模型系統振動的不良影響，測壓法得到的結果較之測力法更接近Sears函數，因而更加可信(尤其在高頻區)。

(4) 對于升力和升力矩而言，相比脈動風速w分量相關的氣動導納，脈動風速u分量相關的氣動導納數值明顯要大，甚至會大于1，并且具有較大的離散性。產生這種現象是由于u分量對升力和升力矩的貢獻相對較小，導致最小二乘法的識別精度大幅降低。

5 結 論

本文以準平板斷面為例，直接利用格柵湍流場測壓試驗結果進行橋梁斷面的氣動導納識別，通過比較相同斷面下測力和測壓法的氣動導納識別結果認為直接利用測壓試驗結果識別氣動導納的方法是可行的。此外，采用Bergh-Tijdeman測壓管路系統頻響函數的理論公式對測壓實驗數據進行了修正，通過對比修正前后的識別結果發現，測壓管路頻響特性會使氣動導納在一定頻率區間產生較大偏差，因而有必要對測壓試驗所得數據進行管路修正。

[1] Davenport A G. The application of statistical concepts to the wind loading of structures[C]//Proc ICE, 1961, 19: 449-472.

[2]Davenport A G. Buffeting of a suspension bridge by storm winds[J]. Journal of Structural Division, ASCE, 1962, 88(6): 233-264.

[3] 李思翰. 基于振動翼柵湍流場測力實驗的橋梁斷面氣動導納識別法[D]. 上海: 同濟大學, 2008.

Li Sihan. Identification method of aerodynamic admittances of bridge decks based on force measurement test in oscillating airfoil grid-generated flows[D]. Shanghai: Tongji University, 2008.

[4] 文水兵. 特征湍流效應對典型橋梁斷面脈動氣動力譜和氣動導納的影響[D]. 上海: 同濟大學, 2008.

Wen Shuibing. Effect of signature turbulence on fluctuating aerodynamic force spectra and aerodynamic admittance of typical bridge decks[D]. Shanghai: Tongji University, 2008.

[5] 趙傳亮. 箱形主梁抖振力空間相關性及其對橋梁抖振響應的研究[D]. 上海: 同濟大學, 2009.

Zhao Chuanliang. Spatial correlation of buffeting forces on box decks and its effect on buffeting responses of bridges[D]. Shanghai: Tongji University, 2009.

[6] 任鵬杰. 分離雙幅橋抖振力參數及氣動干擾效應研究[D]. 上海: 同濟大學, 2011.

Ren Pengjie. Parameters of buffeting forces and aerodynamic interference of bridges with two separated decks[D]. Shanghai: Tongji University, 2011.

[7] 徐自然. 基于格柵湍流場節段模型試驗的橋梁斷面六分量氣動導納識別[D]. 上海: 同濟大學, 2014.

Xu Ziran. Identification of six-component aerodynamic admittances of bridge decks via sectional model tests in grid-generated turbulent wind field[D]. Shanghai: Tongji University, 2014.

[8] 徐自然, 周奇, 朱樂東. 考慮模型抖振力跨向不完全相關性效應的氣動導納識別[J]. 實驗流體力學, 2014, 28(5): 39-46.

Xu Ziran, Zhou Qi, Zhu Ledong. Identification of aerodynamic admittances by considering the effect of incomplete span-wise correlation of buffeting forces on sectional model[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(5): 39-46.

[9] Bergh H, Tijdeman H. Theoretical and experimental results for the dynamic response of pressure measuring systems[R]. NLR-TR F. 238, 1965.

[10] Holmes J D, Lewis R E. Optimization of dynamic pressure-measurement systems. Ⅰ. single point measurements[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1987, 25: 249-273.

(編輯：張巧蕓)

Comparison between aerodynamic admittances identified via force and pressure measurement tests

Tan Zhongxu1,2, Zhu Ledong1,2,3,*, Xu Ziran1,2, Chen Wei1,2,3

(1. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 2. Department of Bridge Engineering, Tongji University, Shanghai 200092, China; 3. Key Laboratory of Wind Resistance Technology of Bridges of Transport Ministry, Tongji University, Shanghai 200092, China)

Aerodynamic admittances are important parameters in buffeting analysis, and often identified via wind tunnel test of force or pressure measurement in turbulent wind field. However, both the natural vibration of the balance-model system and the frequency-response effect of the tubing system for pressure measurement can affect the identified results of aerodynamic admittance. In this study, the aerodynamic admittances of a quasi-flat section were identified via wind tunnel tests of force and pressure measurements in conjunction with a least square method based on a colligated-residue composed of buffeting-force auto-spectrum and cross-spectra between buffeting force and fluctuating wind speeds (simplified as “colligated least square method”). The span-wise incomplete correlation effect of buffeting forces on the sectional model was taken into account in the identification of aerodynamic admittance based on the force measurement test. Two cases with and without correcting the frequency-response effect of pressure tubing system according to the Bergh-Tijdeman’s formulae were considered in the identification of

aerodynamic admittance based on the pressure measurement test. On these bases, the influencesof the natural vibration of the balance-model system and the frequency-response effect of the pressure tubing system on the identified results of the aerodynamic admittances were investigated by observing the discrepancies among the test results and the Sears Function, which is the theoretical aerodynamic admittance of flat plate cross section. The results show that the resonance of balance-model system can significantly amplify the identified results of aerodynamic admittances. Furthermore, compared with the results of aerodynamic admittances identified via force measurement test, those identified via the pressure measurement test are much more reasonable in general, and have much wider ranges of reduced frequency with practicable values, because the natural frequency of pressure tubing system is generally much higher than that of the balance-model system. Moreover, the values of the identified aerodynamic admittances would drop to some extent within a concerned range of reduced frequency for buffeting analyses of common long span bridges after considering the correction of frequency-response effect of pressure tubing system, because the resonance effect of tube cavity plays an amplifying role on the fluctuating pressure signals with frequencies lower than the resonant frequency of the tube.

aerodynamic admittance;wind tunnel test; force measurement;pressure measurement;frequency response characteristic of pressure tube

1672-9897(2015)03-0035-06

10.11729/syltlx20140086

2014-07-25;

2015-03-04

國家自然科學基金項目(91215302);科技部國家重點實驗室基金資助系統性項目(SLDRCE08-A-02)

TanZX,ZhuLD,XuZR,etal.Comparisonbetweenaerodynamicadmittancesidentifiedviaforceandpressuremeasurementtests.JournalofExperimentsinFluidMechanics, 2015, 29(3): 35-40. 檀忠旭, 朱樂東, 徐自然, 等. 基于測力和測壓試驗的氣動導納識別結果比較. 實驗流體力學, 2015, 29(3): 35-40.

V211.7

A

檀忠旭(1990-)，女，河北石家莊人，博士研究生。研究方向：橋梁和建筑結構抗風研究。通信地址：上海楊浦區四平路1239號同濟大學風工程館214(200092)。E-mail: tanzhongxu2008@163.com

*通信作者 E-mail: ledong@tongji.edu.cn