空間非均勻加熱Rayleigh-Bénard湍流熱對流的傳熱實驗研究

詹靖華, 周 全

(上海大學 上海市應用數(shù)學和力學研究所, 上海 200072)

空間非均勻加熱Rayleigh-Bénard湍流熱對流的傳熱實驗研究

詹靖華, 周 全*

(上海大學 上海市應用數(shù)學和力學研究所, 上海 200072)

研究了空間非均勻加熱對Rayleigh-Bénard湍流熱對流系統(tǒng)傳熱效率的影響。實驗采用長方體對流槽，以水為流體介質(zhì)。調(diào)節(jié)加熱片的輸入功率，改變系統(tǒng)注入能量的空間分布，對比非均勻加熱與均勻加熱下的湍流傳熱Nu-Ra關系。從實驗結果來看，非均勻加熱條件下Nu數(shù)的提升十分顯著，湍流傳熱效率明顯提高。

Rayleigh-Bénard對流；湍流熱對流；湍流傳熱；非均勻加熱

0 引 言

Rayleigh-Bénard(RB)湍流熱對流系統(tǒng)是從眾多自然現(xiàn)象中抽象出來的研究對流問題的經(jīng)典流體力學模型[1-5]。RB系統(tǒng)的實驗裝置可描述為：在充滿對流介質(zhì)的封閉對流槽內(nèi), 加熱下導板，冷卻上導板，保持上、下導板溫度恒定，當上下導板的溫度差ΔT足夠大時，槽內(nèi)流體將展現(xiàn)出非常復雜的無規(guī)則運動模式，進而形成湍流熱對流。在充分發(fā)展的RB系統(tǒng)中，上下導板附近存在很薄的溫度邊界層，冷熱羽流分別從上下溫度邊界層中生成、分離，并在浮力作用下運動，運動過程中自組織形成大尺度環(huán)流。對于任意一個給定幾何形狀的對流槽而言，系統(tǒng)僅由2個無量綱的控制參數(shù)所決定，即 Ralyeigh數(shù)(Ra)和Prandtl數(shù)(Pr)，分別定義為：

式中:a,v和κ分別為對流介質(zhì)的熱膨脹系數(shù)，運動粘性系數(shù)，熱擴散系數(shù)，g為重力加速度，H為對流槽上下板的距離。Ra數(shù)是系統(tǒng)無量綱化的溫差；Pr數(shù)表示的則是流體本身的屬性，表征流體的動量擴散與熱擴散之間的相對強弱。系統(tǒng)對流傳熱的響應參數(shù)是Nusselt數(shù)(Nu)，定義為：

Nu=J/(λΔT/H)

式中:J為熱流量密度，λ為對流介質(zhì)的熱導系數(shù)。Nu數(shù)表征對流傳熱的效率，是通過對流槽的實際熱通量J與系統(tǒng)中只存在熱傳導時的熱通量λΔT/H的比值。Nu是Ra數(shù)和Pr數(shù)的函數(shù)，即Nu(Ra,Pr)。

RB系統(tǒng)中的核心問題之一就是湍流傳熱，即Nu數(shù)隨著Ra數(shù)和Pr數(shù)的變化規(guī)律。1989年，Libchaber研究組開展“芝加哥對流實驗”[6-8]，該實驗揭示當Ra>5×105時系統(tǒng)內(nèi)的流體流動將進入湍流狀態(tài)，此時測得Nu～Ra0.282。1990年，Shraiman & Siggia[9-10]利用大尺度環(huán)流在上下導板附近的統(tǒng)計特性從理論上導出Nu～Ra2/7。2000年，Grossmann & Lohse提出GL模型[11-14]，給出Nu數(shù)與Ra數(shù)和Pr數(shù)關系的二位相圖。他們將系統(tǒng)總能量耗散和溫度耗散分解為邊界層的貢獻和邊界層外其它流體區(qū)域的貢獻，得到Nu數(shù)與Ra數(shù)和Pr數(shù)的關系。此模型陸續(xù)得到了很多實驗數(shù)據(jù)的驗證。

在經(jīng)典的RB模型中，對流槽上下導板均勻加熱。然而，自然界中的很多湍流流動都受到非均勻的外力驅(qū)動，一個簡單的例子，人體血管內(nèi)血液的流動是受到周期性心跳所產(chǎn)生的壓力的驅(qū)動，這便是一種時間非均勻外力驅(qū)動的湍流流動。近年來有關這方面的實驗研究也漸漸興起，Jin & Xia[15]研究了脈沖能量輸入下的RB系統(tǒng)的湍流傳熱特性，發(fā)現(xiàn)當能量輸入的脈沖頻率為大尺度環(huán)流頻率的2倍時，Nu數(shù)大幅增加，推測其原因是由于羽流的生成與大尺度環(huán)流發(fā)生共振。除時間非均勻外力驅(qū)動湍流外，空間非均勻外力驅(qū)動的湍流流動在自然界中也很常見，比如大氣環(huán)流受到太陽輻射的加熱，這類外驅(qū)動力在不同的經(jīng)緯度上的強度是不一樣的。然而，目前還沒有相關的工作研究空間非均勻外力驅(qū)動下的RB系統(tǒng)傳熱。本實驗的主要目的就是研究空間非均勻加熱條件下的RB系統(tǒng)與傳統(tǒng)均勻加熱系統(tǒng)相比，在湍流傳熱效率上的差異。

1 實驗裝置和實驗條件

1.1 實驗裝置

如圖1(a)和(b)所示，本研究采用長方體對流槽，其水平橫截面的長L和寬W分別為24.1cm、6.1cm，垂向高H為24.3cm。對流槽由上下導板和有機玻璃邊壁組成。其中，上導板是一塊厚度為3cm的紫銅板(導熱系數(shù)為400W/mK)，內(nèi)部鑿有2個彎曲槽道(見圖1(c))，槽道寬1.2cm、深2cm，相鄰槽道的間距為1.2cm。槽道始于上導板對角線一端，終于另一端。槽道兩端外接水冷機(Polyscience 9702，控溫精度為0.01℃)，水冷機中的水流經(jīng)槽道并循環(huán)往復，從而將上導板的熱量帶走；相鄰槽道內(nèi)的水流方向相反，以使上導板的溫度分布盡量均勻。下導板由2塊厚1cm的紫銅板組成，兩板之間夾有3組厚度約為1mm、大小為8cm×6cm的矩形加熱片，加熱片并排置于對流槽正下方，位置如圖1(d)中斜線部分所示。加熱片兩面均勻涂抹有導熱膠，使其與銅板充分接觸。針對不同的實驗工況，備有2種直流電源供加熱片外接(GPD-3303D，最大輸出功率為90W，最大輸出電壓為30V，穩(wěn)定性99.9%；IPD-6006SLU，最大功率360W，最大輸出電壓60V，穩(wěn)定性99.9%)。邊壁由4塊厚度約為7.4mm的有機玻璃拼接制作而成。導板與邊壁之間置有厚約2mm的硅膠墊片，防止對流槽漏水。對流槽上下導板內(nèi)各置有12個半導體測溫探頭，探頭的埋設深度為整個導板寬度的1/3，其位置如圖1(b)和(d)所示，其中位于導板同一側的6個測溫探頭等間距分布。利用萬用表(Keithley 2700)采集測溫探頭的電阻數(shù)據(jù)并存入電腦。再利用探頭的溫度-電阻標定曲線，借由Matlab程序，將電阻數(shù)據(jù)轉化為溫度數(shù)據(jù)以進行相關計算。另外，為了減少系統(tǒng)漏熱，對流槽外包裹有3層厚度均為2cm的泡沫塑料。

(a) 長方體對流槽

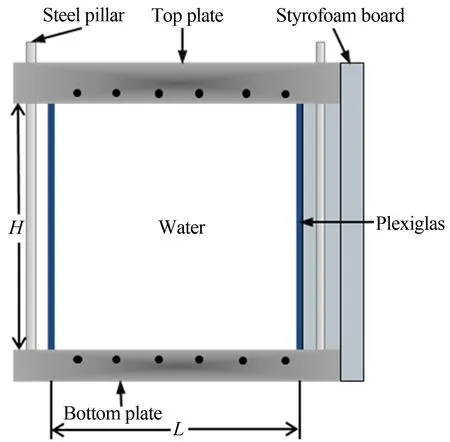
(b) 對流槽示意圖(圖中黑點代表了測溫探頭所在位置)

(c) 上導板內(nèi)槽道分布

(d) 下導板示意圖(實線和虛線代表測溫探頭，斜線部分代表3塊加熱片)圖1 實驗裝置圖Fig.1 Experiment setup

1.2 實驗條件及非均勻加熱處理

實驗以水為對流介質(zhì)。在均勻加熱的對照實驗中，對流介質(zhì)的平均溫度Tm為30.2℃，對應的Pr數(shù)為Pr=5.40。通過調(diào)節(jié)水冷機制冷溫度，及加熱片功率，改變上下導板的溫差ΔT，從而改變系統(tǒng)Ra數(shù)。根據(jù)定義，Nu數(shù)可由實驗測得的溫差ΔT、供給下導板的熱流量密度J(加熱功率除以下導板的面積)及平均溫度Tm下的對流介質(zhì)的熱傳導系數(shù)λ計算得出。實驗中，分別測量了9×108≤Ra≤7×109范圍內(nèi)的11組不同Ra數(shù)下(對應上下導板的溫差范圍為2.5℃≤ΔT≤20.0℃)對應的Nu數(shù)。根據(jù)前文提到的“芝加哥對流實驗”[6-8]的結果可知本實驗所測量工況的Ra數(shù)均處于湍流對流狀態(tài)Ra數(shù)區(qū)間。對于每一組Ra數(shù)，在系統(tǒng)運行5～10h后開始采集數(shù)據(jù)，以保證對流槽內(nèi)湍流流動充分發(fā)展，數(shù)據(jù)采集時間約為10～15h，采樣頻率約為0.8Hz。

在非均勻加熱實驗中，對應于均勻加熱對照實驗中的每一個溫差ΔT，保證水冷機制冷溫度及加熱片總功率都分別與對照實驗相同，調(diào)節(jié)3組加熱片的功率，使其成線性分布，以達到非均勻加熱效果。定義相鄰加熱片間的功率差值ΔP與加熱總功率P之比為δ(ΔP/P)，用以描述非均勻加熱的強度。根據(jù)定義，有0≤δ≤1/3。數(shù)據(jù)采集時間及采樣頻率同對照實驗。

2 實驗結果及分析

2.1 非均勻加熱效果

圖2、3分別為溫差ΔT=4.2℃時，不同非均勻加熱強度δ下，無量綱化的上下導板溫度分布。可以看到溫差為4.2℃時，上導板的溫度分布在δ=0(即均勻加熱)，δ=1/6及δ=1/3時幾乎沒有什么差別，其溫度 (T-Ttop)/ΔT在±2%內(nèi)變化(見圖2中虛線)，這一溫度分布脈動與國際上的類似實驗數(shù)據(jù)相符[16]，說明了在本實驗中上導板的溫度的確近似滿足均勻分布的條件。這還說明了改變下導板加熱片的功率分布對上導板溫度分布的影響很小。這是因為，一方面對流槽內(nèi)的湍流流動使得不同溫度的流體充分混合；另一方面，上導板由水冷機水循環(huán)制冷，而水冷機的制冷溫度并沒有改變。在這2個因素的共同影響下，上導板的溫度不會發(fā)生很大變化。下導板的溫度分布則有了很大變化。從圖中可以看到，在δ=0時，下導板的溫度接近均勻分布，而在δ=1/6時，下導板的溫度分布明顯變得不均勻，呈線性分布。當δ=1/3時，這一線性分布更加明顯，下導板最低最高溫度相差近0.18ΔT。

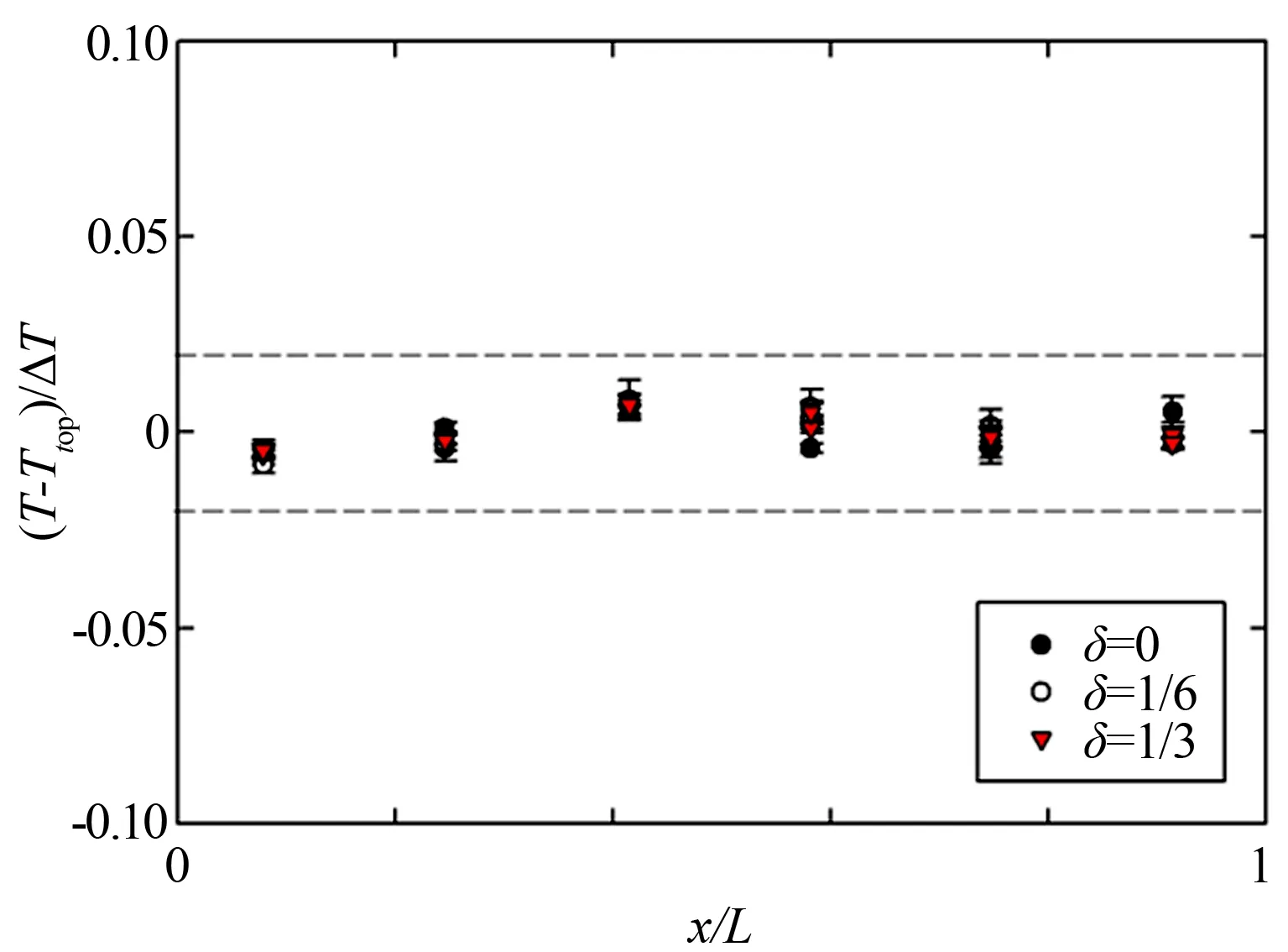
圖2 ΔT=4.2℃，δ=0、1/6、1/3上導板溫度分布

Fig.2 Temperature distribution in the top plate at ΔT=4.2℃ for differentδ

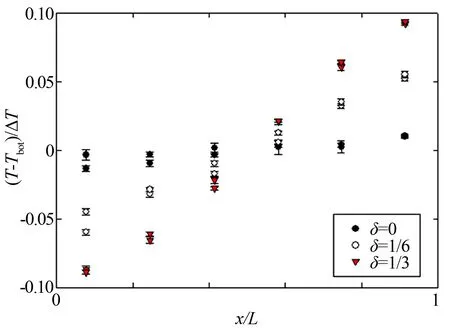
圖3 ΔT=4.2℃，δ=0、1/6、1/3下導板溫度分布

Fig.3 Temperature distribution in the bottom plate at ΔT=4.2℃ for differentδ

圖4和5分別為溫差ΔT=15.0℃時，不同非均勻加熱強度δ下，無量綱化的上下導板溫度分布。上導板溫度分布基本無變化。下導板溫度在δ=0時近似均勻分布，而在δ=1/6、1/3時呈線性分布，且在δ=1/3時，下導板最低最高溫度相差最大，接近0.22ΔT。

從以上不同溫差ΔT、不同非均勻加熱強度δ下的上下導板溫度分布圖(圖2～5)可以看出，本實驗的非均勻加熱處理是可行的，實際效果十分顯著。

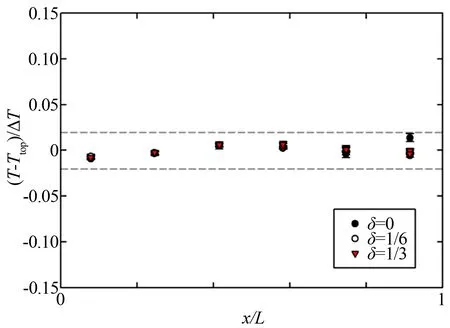
圖4 ΔT=15.0℃，δ=0、1/6、1/3上導板溫度分布

Fig.4 Temperature distribution in the top plate at ΔT=15.0℃ for differentδ

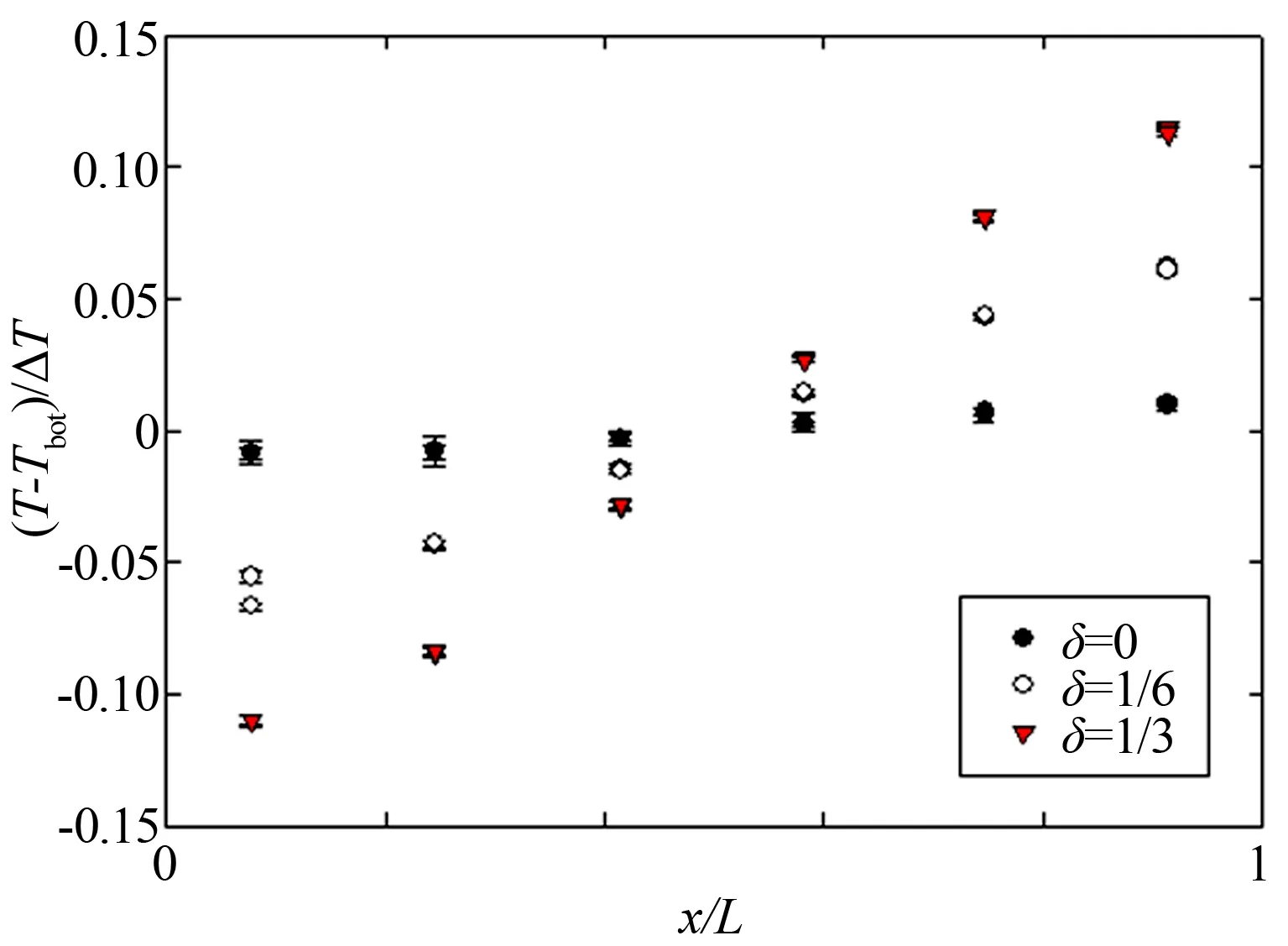
圖5 ΔT=15.0℃，δ=0、1/6、1/3下導板溫度分布

Fig.5 Temperature distribution in the bottom plate at ΔT=15.0℃ for differentδ

2.2 非均勻加熱對Nu數(shù)的影響

圖6為雙對數(shù)坐標中，3種不同非均勻加熱強度條件下，測得的Nu數(shù)隨Ra數(shù)的變化情況。δ=0，即均勻加熱情況下，Nu數(shù)隨Ra數(shù)的增加而增加，且Nu數(shù)與Ra數(shù)存在著Nu～Ra0.286這一標度律關系，這與“芝加哥對流實驗”Nu～Ra0.282及Shraiman & Siggia得到的Nu～Ra2/7都非常接近，說明本研究均勻加熱對照組得到的數(shù)據(jù)誤差很小。再來看δ=1/6，1/3時的數(shù)據(jù)，這2組數(shù)據(jù)普遍大于對照組δ=0時的數(shù)據(jù)，且δ=1/3時的數(shù)據(jù)也要普遍大于δ=1/6時的數(shù)據(jù)。為了更加精確地研究不同δ下的湍流熱輸運效率，圖7中給出了Nu/Ra0.286隨Ra數(shù)的變化情況，均勻加熱對照組數(shù)據(jù)的誤差約為2%。對比相近Ra數(shù)下Nu/Ra0.286的大小，可以看出與均勻加熱相比，非均勻加熱條件下，Nu數(shù)明顯有所提升，最大達到了13%。而對比不同非均勻加熱強度δ下的數(shù)據(jù)，可發(fā)現(xiàn)δ越大，Nu數(shù)的提升越顯著。非均勻加熱δ=1/6時，可以很清楚地看到Nu/Ra0.286隨著Ra數(shù)的增大而增大，在δ=1/3時也有相同趨勢，這說明了非均勻加熱時，Ra數(shù)越大，Nu數(shù)相較均勻加熱時的提升也越大。

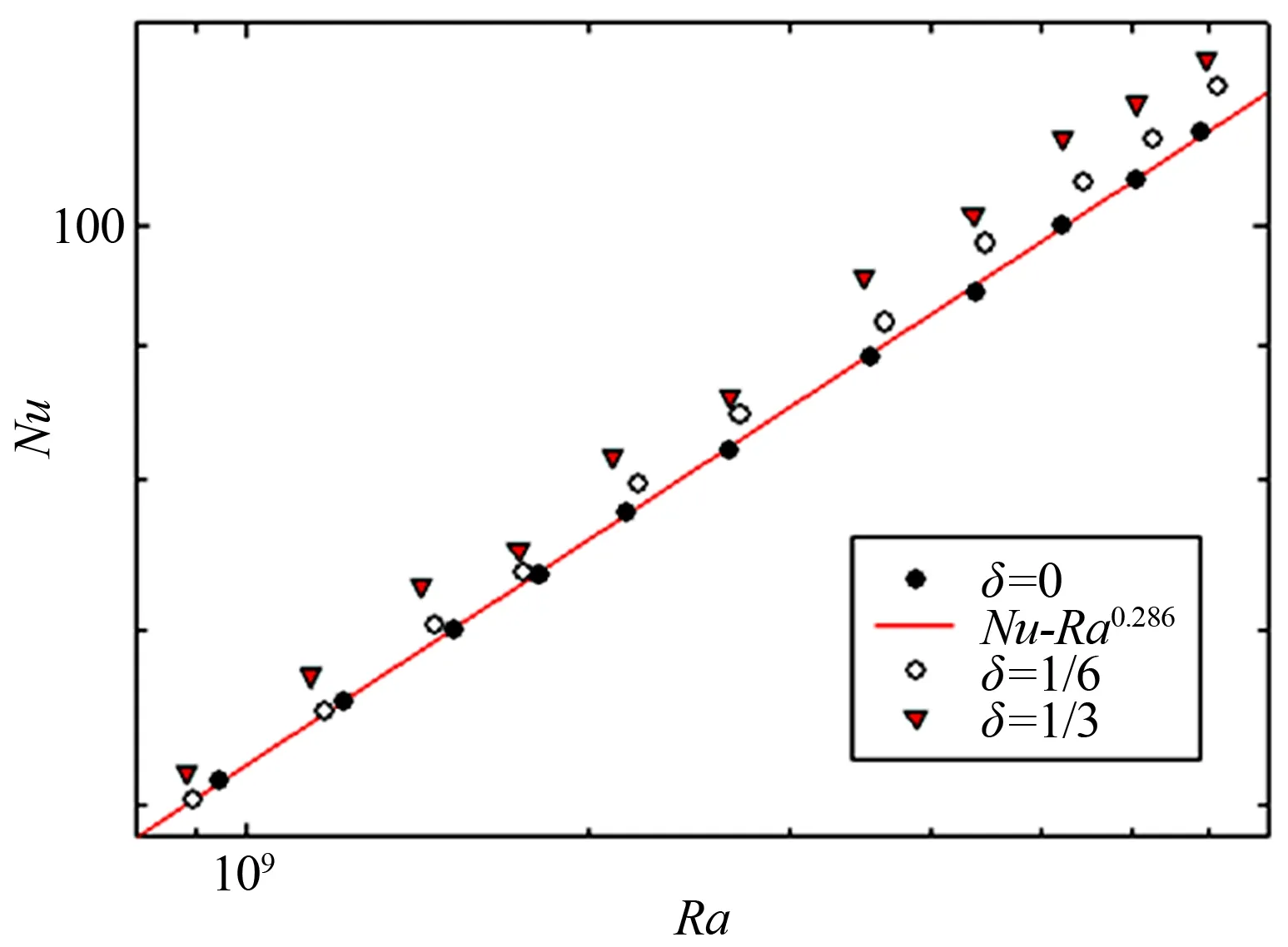
圖6 雙對數(shù)坐標下Nu數(shù)隨Ra數(shù)的變化情況Fig.6 A log-log plot of Nu as a function of Ra

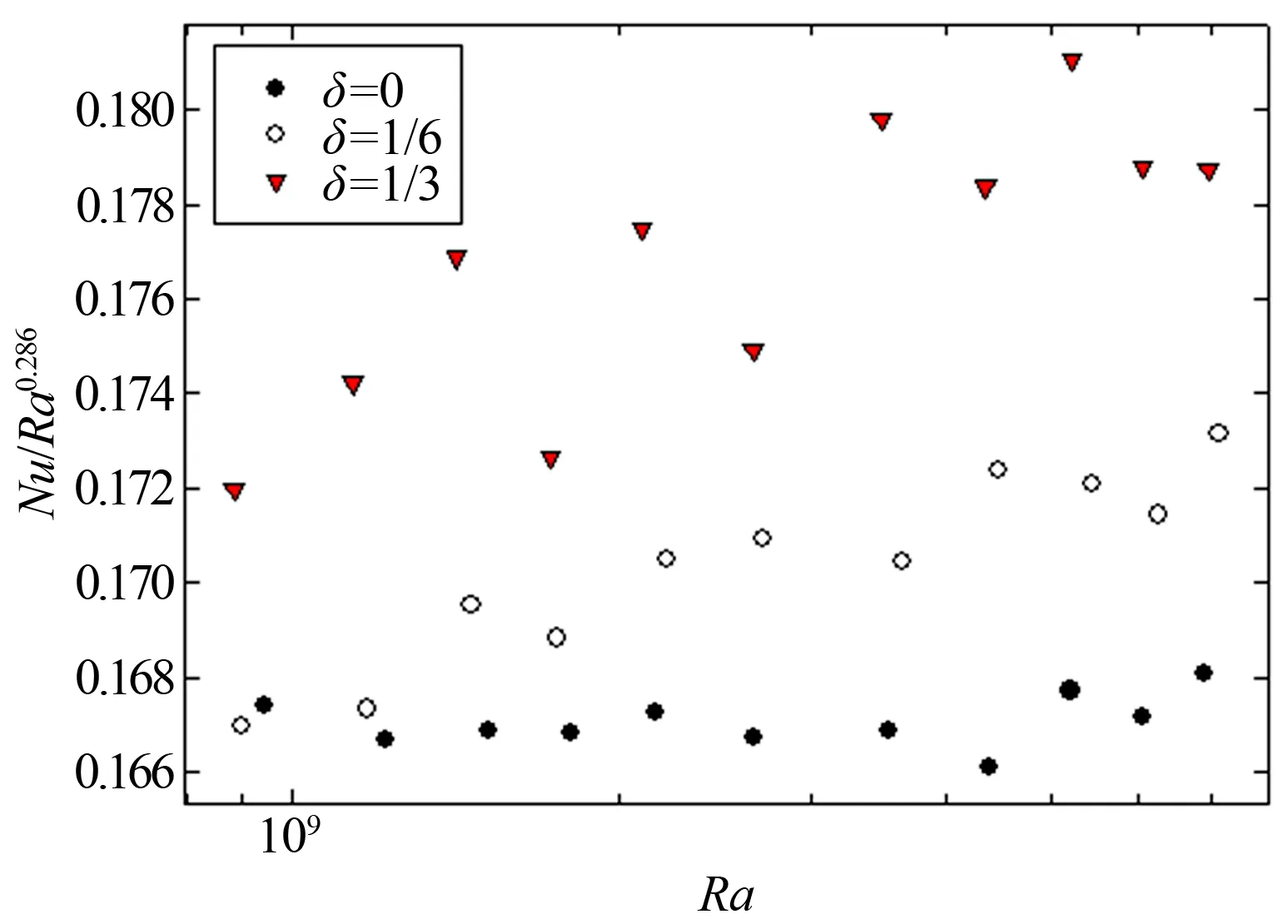
圖7 Nu/Ra0.286隨Ra的變化情況Fig.7 A semilog plot of Nu/Ra0.286 as a function of Ra

2.3Nu數(shù)提升原因分析

Shang等[17-19]在實驗中發(fā)現(xiàn)RB系統(tǒng)的熱輸運主要集中在對流槽邊壁附近，表明系統(tǒng)熱量主要是通過邊壁附近的冷熱羽流向上輸運的。羽流產(chǎn)生于溫度邊界層中，故而系統(tǒng)熱量輸運與溫度邊界層緊密相關。2.1節(jié)的結果表明，在線性非均勻加熱條件下，下導板的溫度呈線性分布，進而導致其溫度邊界層也是一側溫度較高一側溫度較低。那么，當系統(tǒng)得到充分發(fā)展后，熱羽流必定在下導板溫度邊界層中溫度較高一側不斷生成，并在浮力作用下沿著邊壁附近向上運動，最終將熱量傳導至上導板溫度邊界層；冷羽流則在上導板溫度邊界層中產(chǎn)生，在浮力作用下沿著另一側邊壁附近向上運動，最終抵達下導板溫度邊界層中溫度較低一側。在熱羽流生成的一側，該處溫度高于下導板的平均溫度，故而該處實際上下導板溫差要高于系統(tǒng)的平均溫差ΔT，因此熱羽流生成的頻率大大提升，系統(tǒng)傳熱的效率Nu數(shù)隨之提升。結合圖4、圖6，同一溫差(即Ra數(shù))下，非均勻加熱強度“δ” 越大，下導板上的最高溫度越高，故而熱羽流生成一側的實際溫差越大，Nu數(shù)提升也越顯著。與之同理，對比同一非均勻加熱強度“δ”數(shù)據(jù)，可以看到溫差越大，下導板上的最高溫度越高(δ=1/6時此差距很小，δ=1/3時可以則很明顯)，故而Nu數(shù)提升越大。

3 結 論

以長方體Rayleigh-Bénard湍流熱對流系統(tǒng)為研究對象，通過改變下導板加熱片的功率分布改變下導板的溫度分布，精確測量了系統(tǒng)湍流傳熱效率Nu數(shù)，研究了非均勻加熱對Nu數(shù)的影響。實驗結果表明：在非均勻加熱情況下，Nu數(shù)得到了提升，且加熱片的功率分布越不均勻，Nu數(shù)的提升越顯著，在本實驗中Nu數(shù)的提升最大達到13%。值得注意的是，非均勻加熱時，上下導板溫差越大，Nu數(shù)的提升會更加明顯。筆者推測Nu數(shù)獲得提升的原因是，在線性非均勻加熱狀態(tài)下，左右不對稱的下導板溫度邊界層促進了熱羽流的生成，進而提高了傳熱效率。

當然，此結論只是基于線性非均勻加熱的實驗結果的推論，這只是初步的研究方向，后續(xù)也將嘗試其它實驗方法和空間非均勻加熱方式。我們認為上述結論同樣適用于其他的加熱方式，因為不論采用何種非均勻加熱方式，下導板溫度邊界層必定會發(fā)生變化，必然會影響到熱羽流的生成。同時，也期待能夠得到更多相關實驗的驗證。

[1] 王晉軍, 夏克青. Rayleigh-Bénard 湍流對流實驗研究進展[J]. 力學進展, 1999, 29(4): 557-566.

Wang Jinjun, Xia Keqing. Advances in experinmental investigation of Rayleigh-Bénard turbulent convection[J]. Advances in Mech, 1999, 29(4): 557-566.

[2] 周全, 孫超, 郗恒東, 等. 湍流熱對流中的若干問題[J]. 物理, 2007, 36(9): 657-663.

Zhou Quan, Sun Chao, Xi Hengdong, et al. Various issues in turbulent thermal convection[J]. Physics, 2007, 36(9): 657-663.

[3] Ahlers G, Grossmann S, Lohse D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection[J]. Rev Mod Phys, 2009, 81: 503-537.

[4] Lohse D, Xia Keqing. Small-Scale properties of turbulent Rayleigh-Bénard convection[J]. Annu Rev Fluid Mech, 2010, 42: 335-364.

[5] 周全, 夏克青. Rayleigh-Bénard湍流熱對流研究的進展、現(xiàn)狀及展望[J]. 力學進展, 2012, 42(3): 231-251.

Zhou Quan, Xia Keqing. Advances and outlook in turbulent Rayleigh-Bénard convection[J]. Advances in Mech, 2012, 42(3): 231-251.

[6] Heslot F B, Castaing B, Libchaber A. Transition to turbulence in helium gas[J]. Phys Rev A, 1987, 36: 5870-5873.

[7] Castaing B, Gunaratne G, Heslot F, et al. Scaling of hard thermal turbulence in Rayleigh-Bénard convection[J]. J Fluid Mech, 1989, 204: 1-30.

[8] Sano M, Wu X Z, Libchaber A. Turbulence in helium gas gree-convection[J]. Phys Rev A, 1989, 40: 6421-6430.

[9] Siggia E D. High Rayleigh number convection[J]. Anni Rev Fluid Mech, 1994, 26: 137-168.

[10] Shraiman B I, Siggia E D. Heat transport in high-Rayleigh-number convection[J]. Phys Rev A, 1990, 42: 3650-3653.

[11] Grossmann S, Lohse D. Scaling in thermal convection: A unifying view[J]. J Fluid Mech, 2000, 407: 27-56.

[12] Grossmann S, Lohse D. Thermal convection for large Prandtl number[J]. Phys Rev Lett, 2001, 86: 3316-3319.

[13] Grossmann S, Lohse D. Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection[J]. Phys Rev E, 2002, 66: 016305.

[14]Grossmann S, Lohse D. Fluctuations in turbulent Rayleigh-Bénard convection: The role of plumes[J]. Phys Fluids, 2004, 16: 4462-4472.

[15] Jin Xiaoli, Xia Keqing. An experimental study of kicked thermal turbulence[J]. J Fluid Mech, 2008, 606: 133-151.

[16] Brown E, Nikolaenko A, Funfschilling D, et al. Heat transport in turbulent Rayleigh-Bénard convection: effect of finite top- and bottom-plate conductivities[J]. Phys Fluids, 2005, 17: 075108.

[17] Shang Xiaodong, Qiu Xinliang, Tong Penger, et al. Measured local heat transport in turbulent Rayleigh-Bénard convection[J]. Phys Rev Lett, 2003, 90: 074501.

[18] Shang Xiaodong, Qiu Xinliang, Tong Penger, et al. Measurements of the local convective heat flux in turbulent Rayleigh-Bénard convection[J]. Phys Rev E, 2004, 70: 026308.

[19] Shang Xiaodong, Tong Penger, Xia Keqing. Scaling of the local convective heat flux in turbulent Rayleigh-Bénard convection[J]. Phys Rev Lett, 2008, 100: 2445503.

[20] Bénard H. Les tourbillons cellularies dans une nappe liquide[J]. Rev Gen Sci Pure Appl, 1900, 11: 1261-1271.

[21] Rayleigh L. On convection currents in a horizontal layer of fluid when higher temperature is on the under side[J]. Philos Mag, 1916, 32: 529-543.

[22]Malkus M V R. The heat transport and spectrum of thermal turbulence[J]. Proc R Soc London, Ser A, 1954, 225: 196-212.

[23]Kraichnan R H. Turbulent thermal convection at arbritrary Prandtl number[J]. Phys Fluids, 1962, 5: 1374-1389.

[24] Bodenschatz E, Pesch W, Ahlers G. Recent developments in Rayleigh-Bénard convectio[J]. Annu Rev Fluid Mech, 2000, 32: 709-778.

[25] Sun Chao, Xi Hengdong, Xia Keqing. Azimuthal symmetry, flow dynamics, and heat flux in turbulent thermal convection in a cylinder with aspect ratio one-half[J]. Phys Rev Lett, 2005, 95: 074502.

[26] Sun Chao, Ren Liyuan, Song Hao, et al. Heat transport by turbulent Rayleigh-Bénard convection in 1 m diameter cylindrical cells of widely varying aspect ratio[J]. J Fluid Mech, 2005, 542: 165-174.

[27] Brown E, Nikolaenko A, Funfschilling D, et al. Heat transport in turbulent Rayleigh-Bénard convection: effect of finite top- and bottom-plate conductivities[J]. Phys Fluids, 2005, 17: 075108.

[28] Niemela J J, Sreenivasan K R. Formation of the “superconducting” core in turbulent thermal convection[J]. Phys Rev Lett, 2008, 100: 184502.

[29] Ahlers G, Funfschilling D, Bodenschatz E. Transitions in heat transport by turbulent convection at Rayleigh numbers up to 1015[J]. New J Phys, 2010, 11: 123001.

[30] Zhou Quan,Liu Bofang, Li Chunmei, et al. Aspect ratio dependence of heat transport by turbulent Rayleigh-Bénard convection in rectangular cells[J]. J Fluid Mech, 2012, 710: 260-276.

(編輯：李金勇)

Experimental study of turbulent Rayleigh-Bénard convection under non-uniform heating boundary conditions

Zhan Jinghua, Zhou Quan*

(Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China)

We present an experimental investigation of heat transport by turbulent Rayleigh-Bénard (RB) convection under non-uniform heating boundary conditions. During the measurements, the Rayleigh numberRavaries from 9×108to 7×109and the Prandtl numberPris fixed atPr=5.4. By adjusting the spatial distribution of the heating power in the lower plate, we observed an enhancement in the Nusselt numberNuby 13%. Therefore, our results reveal that the non-uniform heating can enhance the global heat transport efficiency of the system.

Rayleigh-Bénard convection;turbulent thermal convection;heat transport;non-uniform heating

1672-9897(2015)04-0047-06

10.11729/syltlx20140141

2014-12-03;

2015-03-31

國家自然科學基金資助項目(11222222);中組部“青年拔尖人才支持計劃”;教育部“新世紀優(yōu)秀人才支持計劃”;上海市“曙光計劃”資助項目(13SG40);上海市教委科技創(chuàng)新計劃(13YZ008)

ZhanJH,ZhouQ.ExperimentalstudyofturbulentRayleigh-Bénardconvectionundernon-uniformheatingboundaryconditions.JournalofExperimentsinFluidMechanics, 2015, 29(4): 47-51,57. 詹靖華, 周 全. 空間非均勻加熱Rayleigh-Bénard湍流熱對流的傳熱實驗研究. 實驗流體力學, 2015, 29(4): 47-51,57.

O357.5

A

詹靖華(1991-)，男，安徽金寨人，碩士研究生。研究方向：Rayleigh-Bénard湍流熱對流。通信地址：上海市延長路149號力學所(200072)。E-mail：lyjy@shu.edu.cn

*通信作者 E-mail: qzhou@shu.edu.cn