不同節點尺度下基于共同鄰居的功能腦網絡建模方法研究

楊艷麗，郭 浩，李海芳,鄧紅霞

(太原理工大學 計算機科學與技術學院，太原 030024)

不同節點尺度下基于共同鄰居的功能腦網絡建模方法研究

楊艷麗，郭 浩，李海芳,鄧紅霞

(太原理工大學 計算機科學與技術學院，太原 030024)

采用腦網絡的結構特性與功能特性相結合的建模方法,探索了3種不同節點尺度下的建模效果好壞。結構特性采用解剖距離;功能特性采用共同鄰居這一相似性指標，從腦網絡的全局屬性與局部屬性的角度分析了建模效果,并提出了一種評估構建的模型網絡與真實網絡的擬合相似程度的指標E值。結果表明,采用共同鄰居相似性這一指標,在3種尺度下構建的腦網絡與真實網絡的屬性擬合程度不同,90個節點下的擬合程度最好,其他2種次之。

多尺度;功能腦網絡建模;解剖距離;共同鄰居;網絡相似度

人腦是一個復雜多變的系統,與之相似的還包括銷售、生態、公共交通、計算機網絡等,這些系統均可以采用不同的方法來定義網絡的節點和邊。利用復雜網絡基本原理[1]以及統計物理學[2]等方法進行拓撲屬性分析,以期發現網絡基本屬性及節點間潛在的拓撲關系。

近年來,越來越多關于腦網絡結構和功能特性的關系[3],取得了顯著的成果。很多神經疾病被證實了與人腦的結構和功能拓撲異常相關[4]。因此,在不同尺度下來研究結構腦網絡與功能腦網絡的拓撲屬性以及它們之間存在怎樣的關系是非常重要的。

不同的節點定義,將直接影響全腦網絡功能特化的解釋。同時,網絡的拓撲屬性也受網絡節點尺度的影響。目前的研究中,節點定義方法主要采用的是利用先驗的解剖模板,來進行腦區的劃分。如AAL[5]、ANIMAL[6]模板等。這些模板往往是針對某一個或幾個樣本,人為的進行腦區的分割,再通過標準化方法,映射到新的樣本中。這一方法簡單有效,但卻存在一定的缺陷。為了避免上述問題的出現,一些研究提出了新的節點定義方法。Hagmann[7]利用DTI影像數據,通過隨機種子點方法,定義了506,1 013,2 026以及4 052等4種不同節點規模模板。利用相同的方法,Honey[8]定義了低分辨率(66個節點)和高分辨率(998個節點)兩個模板。不同尺度的節點規模對功能連接的計算產生極大影響的同時,對網絡的拓撲屬性仍然具有決定性的作用[9]。選擇合理的節點規模,是我們理解網絡拓撲屬性及相關結論的重要前提。

2010年,Newman[10]驗證了生成隨機圖的理論模型,即腦區之間存在連接的概率與其之間的結構度有一定的關系。隨后,Hermundstad et al[11]研究發現了一些結構屬性(包括白質流的長度、數量和空間位置)可以作為先驗條件來進行功能連接的預測。2013年,Tewarie[12]利用解剖距離、結構連接和結構度來進行功能連接的預測,結果證明了結構度在預測中發揮了最大程度的作用,其次是解剖距離。越來越多的研究證明,在某種程度上,腦網絡中的結構連接和功能連接存在關聯。Vértes首次鏈路預測指標[13-14]引入了功能腦網絡建模中,其中共同鄰居指標(Common neighbor)是基于局部信息的最簡單的相似性指標。

文中采用在不同的尺度下,將結構特性與功能特性結合構建的功能腦網絡,這里具體是指解剖距離和共同鄰居相似度指標,利用數學公式構建功能腦網絡,目的是能夠找出其最佳擬合。

1 實驗數據及預處理

在本實驗中共采集了28名健康被試腦部的功能磁共振(functional magnetic resonance imaging,fMRI)數據。采集及預處理工作過程均與山西醫科大學第一醫院合作完成。在實驗前,均與所有被試本人簽署了書面協議。

在掃描的過程中,要求被試在清醒放松的狀態下進行。掃描參數設置如下:33 axial slices,repetition time (tR)=2000 ms,echo time (tE)=30 ms,thickness/skip=4/0 mm,field of view (FOV)=192 mm×192 mm,matrix=64 mm×64 mm,flip angle=90°,248 volumes。

數據的預處理過程是通過SPM8(Statistical Parametric Mapping)[15]軟件進行的。(http:∥www.fil.ion.ucl.ac.uk/spm)。具體步驟包括時間片校正;頭動校正(頭動大于3 mm或轉動大于3°而被棄除);空間標準化(圖像進行12維度的優化仿射變換,將其標準化到3 mm體素的MNI標準空間中);低頻濾波(0.06～0.11 Hz,以降低低頻漂移及高頻的生物噪音)。

2 功能腦網絡構建

功能腦網絡構建主要包括:節點的定義,邊的定義及閾值的選擇。

2.1 節點定義

在節點的定義上,以AAL模板為基礎,通過隨機種子的設置,對AAL原有腦區進行細分,以達到不同尺度下節點的定義。具體方法如下:首先,設置N為預期的節點數。在研究中,我們嘗試了250和500兩個尺度下的節點數,加上原有AAL模板90節點的定義,共得到3個不同的節點尺度。接下來,計算得到原有模板的每個腦區占全部腦區的體素比例V；然后,根據預設的節點數N,可計算得到AAL原有腦區可細化的子區域的個數k=VN，即腦區BR在N的節點規模下,應該細分為k個子區域。此后,令腦區BR設置k個隨機種子體素S=S1,S2,S3，…，Sk,然后依次計算全部余下的體素與Si種子體素的距離。在此采用動態隨機種子點的設置方法,即在計算距離之后,當前體素V與距離最近的體素Si組合,形成新的子區域,并且將V和Si的物理中心設置為生成新的種子體素。依次循環,直至腦區內所有體素均劃分完成。至此,腦區BR便完成了k的劃分。當所有腦區劃分完成后,便可完成預期節點尺度N下的腦區劃分。

需要注意的是,在腦區劃分時,目前采用的方法下,只面對獨立的AAL腦區劃分。對于AAL模板中相鄰腦區,即便其體素距離更近,我們仍不進行劃分。此外,子區域個數k可能不是一個整數。在這種情況下,采用四舍五入方式進行。所以,實際生成的節點數與預期設置N會存在細微的偏差。

將上述過程重復2次,分別設置N為250和500。三個尺度下,所得到的腦區個數分別為256和497。結合原有AAL模板,共完成了3種節點尺度的定義,分別標記為AAL90,Parc256以及Parc497。其中前綴AAL表示采用原有AAL模板,Parc表示此定義采用上述算法生成。

2.2 邊的定義

本文網絡中邊的定義采用了皮爾遜相關系數。首先,為了去除由于頭動引起的偽差異,將每個節點的平均時間序列進行多元線性回歸分析。然后,將其結果殘差做兩兩皮爾遜相關,具體是:

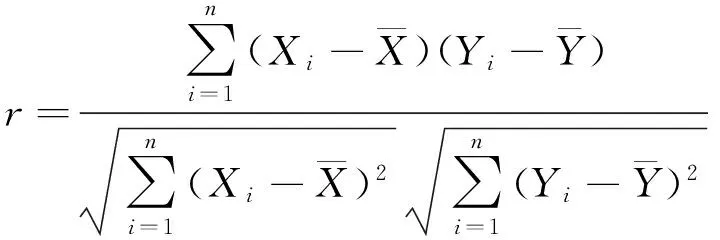
(1)

式中,Xi和Yi分別表示體素i和體素j的時間序列。最后根據閾值將所得的關聯矩陣轉換為對應的二值矩陣。

2.3 閾值選擇

在復雜網絡比較研究中,由于圖的規模及連接密度決定了度量指標的量化值，所以在進行復雜網絡之間的拓撲屬性的定量比較之前,必須對其進行控制。實驗中,對閾值的設置采用稀疏度S,即網絡中實際存在的邊數與網絡中可能存在的最大邊數的比值。由于腦網絡是表現出典型的小世界屬性的低消耗網絡,所以利用這一基本特性,來進行閾值空間的設定,這樣在保證小世界屬性的同時,最大程度的去掉偽連接。其具體規則如下:

所有節點的平均度(節點的度是指所有連接到該節點的邊的數量)大于2×ln(N)。此時N為網絡中的節點數量。

小世界標量σ>1.1(小世界標量定義見下節)。

由于研究中采用了3種不同的節點尺度的定義,其節點數各不相同。那么,根據上述原則所得的閾值空間,在3種節點尺度下并不完全一致。為了研究的可比性,在統一的空間,我們統一采用了90個節點下的閾值空間S∈(8 %,32 %)作為標準空間進行比較,并以步長為0.1在所有稀疏度下,構建腦功能網絡。

3 基于共同鄰居指標的功能腦網絡建模

本文采用的是基于解剖距離及共同鄰居指標的功能腦網絡建模方法。將解剖距離和共同另據指標作為參數,利用數學公式構建腦網絡功能連接。

3.1 功能腦網絡建模方法

本實驗采集了28例健康被試的fMRI數據。為了避免被試之間的差異,數學建模在所有被試的均值網絡上進行,并且選出最優模型。隨后再將最優模型得到的參數映射到每個被試,最終構建每個被試的最優網絡模型,并且利用最優網絡模型來評價建模效果。

本文沿用了Vértes提出的基于結構特性和功能特性相結合的功能腦網絡構建方法,其數學建模公式2所示。其中結構特性采用的是解剖距離,功能特性采用的是共同鄰居這一相似性指標。

Pi,j∝(Si,j)γ×(di,j)-η.

(2)

式中：Si，j為共同鄰居指標;di,j為解剖距離;γ和η是常數參數。實驗中參數的取值范圍設置為[0,3],將步長為0.1。

3.2 網絡相似度評價標準

構建的腦網絡模型與真實網絡之間的相似度如何評價是值得深思的一個問題。Vértes et al在構建模型時就提出利用E值計算網絡相似度,其計算公式為:

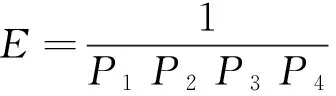
(3)

式中：P1，P2，P3，P4分別為模型網絡與真實網絡屬性之間進行組間t檢驗得到的P值。

之后,Roger Guimer[16]利用相對誤差來評估重構網絡與真實的網絡之間存在的差異。具體是假設真實網絡的屬性為Vt;重構網絡的屬性為Vm,相對誤差的計算如式(4)所示。

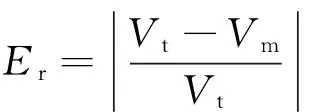
(4)

本文結合上述兩種方法,提出了一種新的計算方法,如式(5)所示。

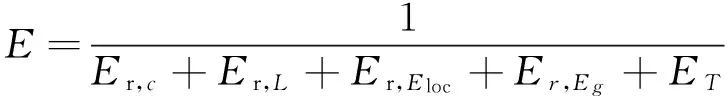
(5)

大量的網絡指標可以從不同層面刻畫網絡的拓撲屬性。研究中,我們選擇了幾種較為基礎的指標，特征路徑長度(Characteristic Path Length,l),全局效率(Global Efficiency,Eg),局部效率(Local Efficiency,Eloc),聚合系數(Clustering Coefficient,C),傳遞性(Transitivity,T)。其中,特征路徑長度和全局效率是全局屬性,其余為局部屬性。根據上述公式,顯而易見E值越大,其構建的網絡模型與真實網絡之間的相似度越高。

最優模型是指在不同稀疏度下,所對應的使E值最大的參數對γ和η。實驗中設置的稀疏度為5%～40%,以5%為步長,共8個不同的稀疏度。因此,每個尺度下,利用均值網絡建模共得到8個最優模型。

4 實驗結果及分析

在三種不同尺度下,采用共同鄰居這一相似性指標和解剖距離進行腦功能網絡建模,并且進行了腦網絡全局和局部屬性擬合相似度的分析,評估了建模效果的優劣。

4.1 網絡屬性擬合

圖1顯示了在三種不同尺度下構建的模型網絡與真實網絡屬性的平均相對誤差。首先,在每個尺度下,我們計算了所有被試在8個稀疏度下的網絡屬性的相對誤差,然后求均值得到每個被試平均相對誤差。

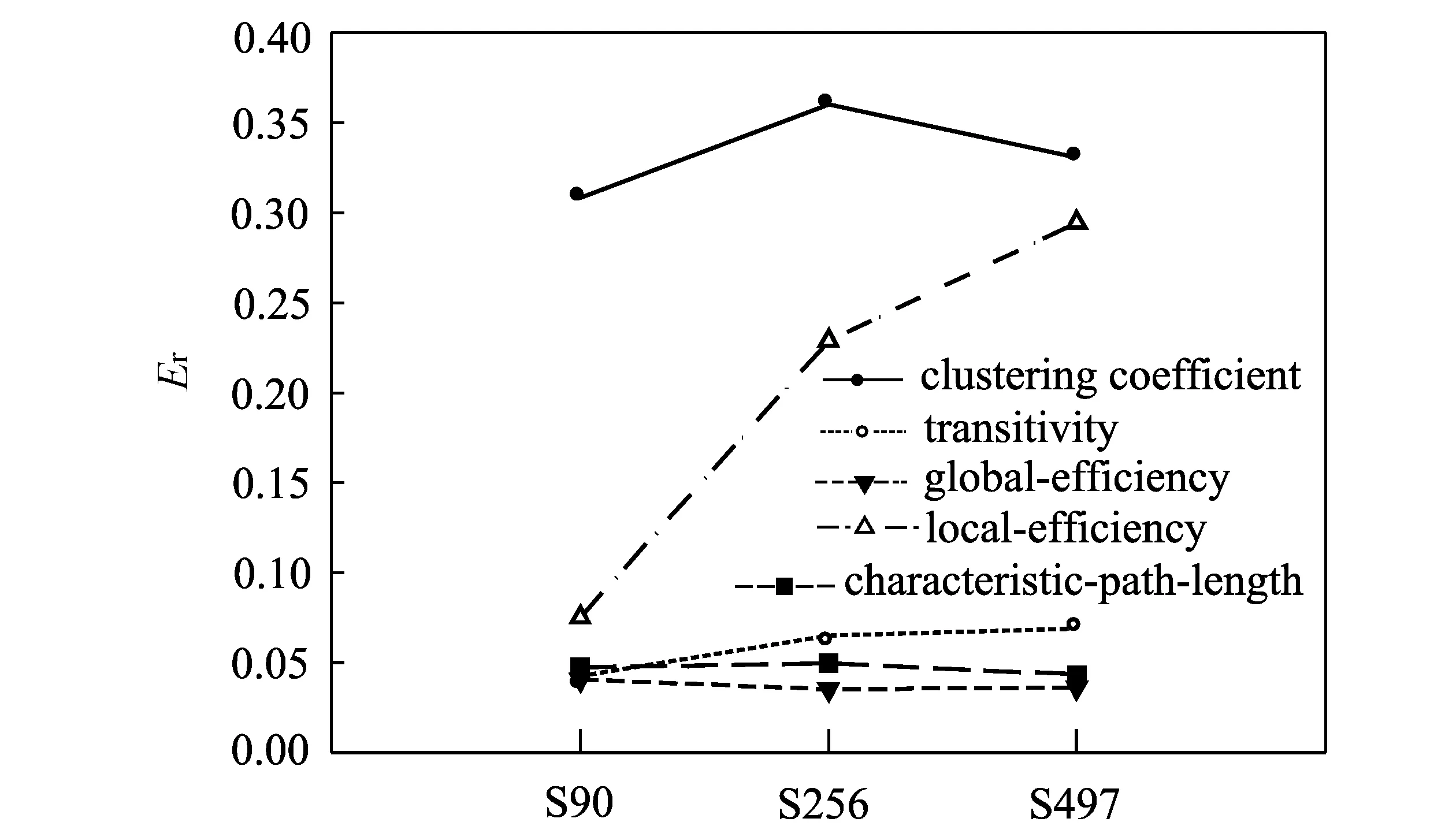
圖1 三種不同尺度下模型屬性與真實屬性的相對誤差

建模結果表明,總體來說,在三個不同尺度下,90個節點構建的腦網絡與真實網絡屬性的擬合效果最好。

從網絡屬性上來說,無論在哪種尺度下,特征路徑長度、全局效率和傳遞性這三種屬性的擬合效果都比較理想,相對誤差較低。而局部效率屬性的擬合效果在90個節點的尺度下其擬合效果較好,在256和497個節點尺度下,相對誤差會急劇增大。聚合系數這一屬性在三種不同尺度下其擬合效果都比較差,相對誤差都高。

4.2 網絡相似度的評價(E值)

三種尺度下構建的模型網絡與真實網絡之間的相似性擬合程度通過E值來評估,詳見圖2。

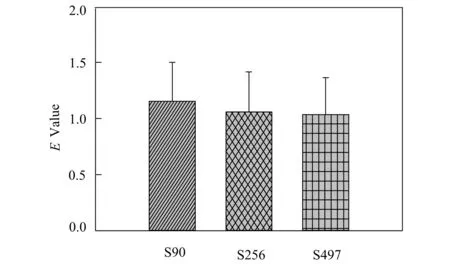
圖2 三種不同尺度下模型網絡與真實網絡整體相似度E值

從圖中可以看出,在三種尺度下的相似度E值差別不是很明顯。90個節點的尺度下模型網絡與真實網絡的相似程度稍高,其次是256和497這兩種節點尺度下相似程度。

5 結論

主要研究了不同尺度下,采用共同鄰居指標在功能腦網絡建模中的應用。建模方法是將腦網絡的結構與功能特性相結合的數學方法。實驗結果顯示三種尺度下,對腦網絡全局或局部屬性的擬合效果不同。從整體擬合程度來看,90個節點構建的腦網絡與真實網絡擬合效果最好,其他兩種次之。此外,利用E值來評價網絡相似度,是否還有更好的評價指標有待探索。并且,本文對所選擇的屬性并沒有考慮權重問題,這些問題都會在未來的研究中進行更深一步的研究。

[1] Erd?s P，Rényi A.On random graphs I[J].Publ Math Debrecen,1959,6:290-297.

[2] Albert R,Barabási A L.Statistical mechanics of complex networks[J].Reviews of modern physics,2002,74(1):47-94.

[3] Bullmore Ed,Sporns O.Complex brain networks:graph theoretical analysis of structural and functional systems[J].Nature Reviews Neuroscience,2009,10(3):186-198.

[4] Stam C J,Van Straaten E.C.W.The organization of physiological brain networks[J].Clin Neurophysiol，2012，123(6)：1067-1087.

[5] Tzourio-Mazoyer N,Landeau B,Papathanassion D,et al.Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain[J].Neuroimage,2002，15(1):273-289.

[6] Collins D L,Holmes CJ,Peters TM,et al.Automatic 3-D model-based neuroanatomical segmentation[J].Human brain mapping,1995，3(3):190-208.

[7] Hagmann P,Kurant M,Gigandet X,et al.Mapping human whole-brain structural networks with diffusion MRI[J].PLoS One,2007，2(7):597.

[8] Honey C,Sporns O,Cammoun L,et al.Predicting human resting-state functional connectivity from structural connectivity[J].Proceedings of the National Academy of Sciences,2009，106(6):2035-2040.

[9] Salvador R,Martinez A,Pomaral-clotet E,et al.A simple view of the brain through a frequency-specific functional connectivity measure[J].Neuroimage,2008,39(1):279-289.

[10] Newman M.Networks:An Introduction[J].AstronomischeNachrichten,2010,327(8):741-743.

[11] Hermundstad A M,Bassett D S,Brown K S,et al.Structural foundations of resting-state and task-based functional connectivity in the human brain[J].Proceedings of the National Academy of Sciences,2013,110(15):6169-6174.

[12] Tewarie P,Hillebrand A,Edwin van D,et al.Structural degree predicts functional network connectivity:A multimodal resting-state fMRI and MEG study[J].Neuroimage,2014,97(2):296-307.

[13] Getoor L,Diehl C P.Link Mining:A Survey[J].Sigkdd Explorations Special Issue on Link Mining，2005,7(2):3-12.

[14] Lyu L,Zhou T.Link prediction in complex networks:A survey[J].Physica A Statistical Mechanics & Its Applications,2011,390(6):1150-1170.

[15] Friston K J,Penny W D,Ashburner J T,et al.Statistical Parametric Mapping:The Analysis of Functional Brain Images[M].USA:Academic Press,2011.

[16] Guimera R,Sales-Pardo M.Missing and spurious interactions and the reconstruction of complex networks[J].Proceedings of the National Academy of Sciences,2010,106(52):22073-22078.

(編輯：朱 倩)

Research on Method of Brain Functional Network Modeling Based onCommon Neighbor with different node scales

YANG Yanli，GUO Hao，LI Haifang，DENG Hongxia

(CollegeofComputerScienceandTechnology,TaiyuanUniversityofTechnology,Taiyuan030024，China)

This paper adopts a modeling method combining brain network structural and functional characteristics and explores the modeling effect under three node scales.The structural characteristic uses anatomical distance and functional characteristic uses common neighbor similarity index.We analyze the modeling effect from the global properties and local properties of five kinds of brain network and put forward an indexEas the evaluation of the fitting similarily between model and real networks.Results show the fitting degree under the three node scales is different.The fitting degree for 90 nodes scale is best and the other two is slightly inferior.

multi-scale;brain functional network modeling;anatomical distance;common neighbor;network similarity

1007-9432(2015)06-0760-04

2015-06-26

國家自然科學基金項目:多模態腦功能復雜網絡分析方法及應用研究(61373101),基于解剖距離及節點相似度功能腦網絡建模方法研究(61402318);山西省教育廳高校科技創新項目(20121003),太原理工大學青年基金項目(2012L014，2013T047)

楊艷麗(1987-)，女，太原市人，博士,主要從事智能信息處理、腦信息學的研究，(E-mail)yangyanli0111@163.com

鄧紅霞，女，副教授，主要從事智能信息處理腦信息學研究，(E-mail)denghz@tyut.edu.cn

文獻標識碼:A DOI：10.16355/j.cnki.issn1007-9432tyut.2015.06.022