張量分解在齊次多項式中的應(yīng)用

潘珺珺,盧琳璋

(廈門大學(xué)數(shù)學(xué)科學(xué)學(xué)院,福建廈門361005)

張量分解在齊次多項式中的應(yīng)用

潘珺珺,盧琳璋*

(廈門大學(xué)數(shù)學(xué)科學(xué)學(xué)院,福建廈門361005)

針對n元m次齊次實(shí)系數(shù)多項式,提出了對應(yīng)的m階n維系數(shù)張量的定義,并應(yīng)用張量分解,給出了該類多項式因子分解的充要條件.證明了該類多項式總是可以寫成若干個因式之和,因此通過構(gòu)造系數(shù)張量就能得到所需要的因式之和.

齊次多項式;張量;TT格式

n元m次齊次多項式的研究是一個古老而有意義的課題.在很多方面有著重要的應(yīng)用,比如,由Qi[1-2]和Lim[3]中提出的Z特征值問題,可以轉(zhuǎn)化成多項式最優(yōu)化問題來求解.我們知道對于二次型的研究,矩陣分解有著非常重要的作用.考慮n元m次齊次多項式在實(shí)數(shù)域上的情況,將矩陣在二次型的應(yīng)用自然推廣到張量上.

1 預(yù)備知識

這一節(jié)簡單回顧齊次多項式的定義以及相關(guān)的張量知識.

定義1[4]n元m次齊次多項式(按字典排列)

所謂張量就是高維數(shù)組,例如,向量可看成一階張量,矩陣可看成二階張量,對于m階n維張量∈Rn×n×…×n,我們采用Kolda等在文獻(xiàn)[5]中的定義,記為∈R[m,n].

定義∏m為(1,2,…,m)所有置換的集合,有

定義2[5-6]∈R[m,n]為超對稱張量,如果αi1,i2,…,im=αip(1),ip(2),…,ip(m),其中{i1,i2…,im}∈{1,2,…,n},p∈∏m.

定義3[6]若寫成m個向量外積,即

其中α(i)=[α(i)1,α(i)2,…,α(i)n]∈Rn,“?”表示外積.

定義4[6]設(shè)張量∈R[m,n],向量x∈Rn,二者的乘積定義為

定義5[7-8]張量∈R[m,n]總可以寫成

張量TT-svd分解由Oseledets在文獻(xiàn)[7]提出的,這種分解方式是在張量的展開矩陣的svd分解基礎(chǔ)上進(jìn)行的.我們以3階張量為例,來說明TT分解的過程.

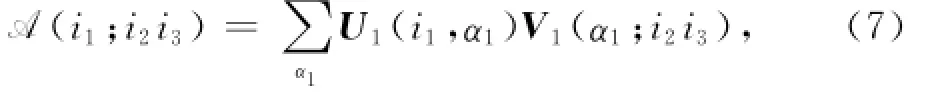
再將矩陣V1重新排列,對重排的V1進(jìn)行奇異值分解,如下:

令U3(α2;i3)=V2(α2;i3),那么有

在MATLAB中,可以直接使用由Oseledets給出的TT工具包[9],任意一個張量的TT分解實(shí)現(xiàn)很簡單,僅需要“TT-tensor”這個命令.

2 主要結(jié)果

令x=[x1,x2,…,xn]∈Rn,那么f(x)可以等價寫為

對任何的{i1,i2…,im}∈{1,2,…,n},p∈∏m,有

若固定{i1,i2…,im},有xj11xj22…xjnn與之對應(yīng),則有

下面舉個例子說明式(12)成立.

例1 設(shè)f(x)是一個二元三次多項式,有

按照式(10),有

則

由式(13),可知:

即式(12)成立.容易知道滿足以上等式的aijk有無數(shù)個.設(shè)(i,j,k)=aijk,顯然∈R2×2×2是一個3階2維張量.

其中bj1,j2,…,jn為式(1)所定義的系數(shù).稱張量為n元m次多項式(1)的系數(shù)張量.易知,對應(yīng)式(1)的系數(shù)張量有無數(shù)個,稱包含所有系數(shù)張量集合為對應(yīng)于多項式(1)的系數(shù)張量集,記為φ().

根據(jù)定義4,多項式(10)可以寫成

當(dāng)m=2時,f(x)為n元2次齊次多項式,f(x)= xTAx,當(dāng)A對稱時便為我們所熟悉的二次型.

定理1 若m次齊次多項式f(x)形如式(1)可以寫成m個一次實(shí)系數(shù)因式的乘積的充要條件是存在秩1張量∈φ().

證明 m=1時,顯然.

當(dāng)m=2時,A為秩1陣?A=αβT,其中α=(α1,…,αn)T,β=(β1,…,βn)T,?

定理2 m次齊次多項式f(x)形如式(1)總是可以寫成若干個因式的和,每個因式為m個一次因式乘積.

其中1≤i1,i2,…,im≤n,A1(i1)∈R1×r1,Ak(ik)∈

Rrkˉ1×rk,Am(im)∈Rrmˉ1×1.則

將y(k)展開,即得.

根據(jù)定理2的證明,容易得到

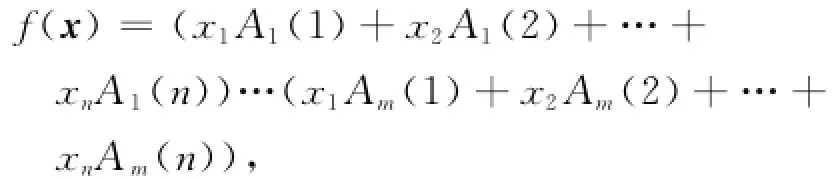
因?yàn)锳k(ik)是數(shù),故f(x)表示成如上的m個一次實(shí)系數(shù)因式的乘積,證得.

我們給出例2,從直觀上來說明上述這些理論.

構(gòu)造系數(shù)張量1:

簡化為

得到f(x)的因式分解.

構(gòu)造系數(shù)張量2:

該系數(shù)向量為超對稱張量.應(yīng)用TT分解,得到

其中A1(i1)∈R1×3,A2(i2)∈R3×3,A3(i3)∈R3×1,i1, i2,i3=1,2,3.令,得到

那么

3 結(jié)論及進(jìn)一步的工作

本文主要討論了張量分解與實(shí)系數(shù)齊次多項式的關(guān)系,提出了對應(yīng)的系數(shù)張量的定義,給出了該類多項式因子分解的充要條件.我們發(fā)現(xiàn)通過構(gòu)造系數(shù)張量,利用張量分解,多項式總是能得到對應(yīng)的因式之和.這些結(jié)論都是由矩陣在n元2次齊次多項式應(yīng)用自然推廣的,但同時對于特征值分解可以將二次型化為標(biāo)準(zhǔn)型這一結(jié)論,張量沒有對應(yīng)的分解方式,對于一般的n次型還無法實(shí)現(xiàn)標(biāo)準(zhǔn)型的轉(zhuǎn)化.這些將是進(jìn)一步的工作.

[1] Qi L.Eigenvalues of a real supersymmetric tensor[J].J Symb Comput,2005,40:1302-1324.

[2] Qi L.Eigenvalues and invariants of tensors[J].J Math A-nal Appl,2007,325:1363-1377.

[3] Lim L H.Singular values and eigenvalues of tensors:a variational approach[J].Proceeding of the IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing,2005,1:129-132.

[4] 北京大學(xué)數(shù)學(xué)系.高等代數(shù)[M].3版.北京:高等教育出版社,2003:34-39.

[5] Kolda T G,Mayo J R.Shifted power method for computing tensor eigenpairs[J].SIAM J Matrix Anal Appl, 2011,32(4),1095-1124.

[6] Kolda T G,Bader B W.Tensor decompositions and applications[J].SIAM REV,2009,51:455-500.

[7] Oseledets I V.Tensor train decomposition[J].SIAM J Sci Comp,2011,33:2295-2317.

[8] Oseledets I V,Tyrtyshnikov E E.Breaking the curse of dimensionality,or how to use svd in many dimensions [J].SIAM J Sci Comp,2009,31:3744-3759.

[9] Oseledets I V.TT-Toolbox 2.2[EB/OL].[2012-01-09]. http://spring.inm.ras.ru/osel/page-id=24.

[10] Lathauwer L D,Moor B D,Vandewalle J.A multilinear singular value decomposition[J].SIAM J Matrix Anal Appl,2000,21:1253-1278.

Applications of Tensor Decomposition in Homogeneous Polynomials

PAN Jun-jun,LU Lin-zhang*
(School of Mathematical Sciences,Xiamen University,Xiamen 361005,China)

:We consider n-variable homogeneous polynomials of degree m with real coefficients.We propose the corresponding coefficient tensors of order m and n-dimension.A necessary and sufficient condition for the polynomial factorization isgiven by using tensor decomposition to its coefficient tensor.We prove that the polynomial can be written as a sum of factors.Therefore,we can obtain the sum we desire by reconstructing its coefficient tensor.

homogeneous polynomial;tensor;TT-format

O 151.23

A

0438-0479(2015)03-0347-04

10.6043/j.issn.0438-0479.2015.03.009

2014-08-14 錄用日期:2014-12-04

國家自然科學(xué)基金(11261012)

*通信作者:lzlu@xmu.edu.cn

潘珺珺,盧琳璋.張量分解在齊次多項式中的應(yīng)用[J].廈門大學(xué)學(xué)報:自然科學(xué)版,2015,54(3):347-350.

:Pan Junjun,Lu Linzhang.Applications of tensor decomposition in homogeneous polynomial[J].Journal of Xiamen University:Natural Science,2015,54(3):347-350.(in Chinese)