冰球式封裝蓄冰槽蓄冷過程理論分析及實驗研究

王 瑾, 趙 凱, 王素英, 趙路平, 段文珊

(1.上海理工大學環境與建筑學院,上海 200093;2.中原工學院信息商務學院,鄭州 450000)

冰球式封裝蓄冰槽蓄冷過程理論分析及實驗研究

王 瑾1, 趙 凱1, 王素英2, 趙路平1, 段文珊1

(1.上海理工大學環境與建筑學院,上海 200093;2.中原工學院信息商務學院,鄭州 450000)

通過對冰球式封裝蓄冰槽蓄冷時的傳熱過程進行分析,建立了數值傳熱方程,對蓄冷過程進行了理論計算,得到了蓄冰槽蓄冷過程中乙二醇溶液出口溫度及蓄冰球溫度的變化趨勢.同時,設計搭建了冰球式封裝蓄冷空調系統實驗臺,分析了冰球式蓄冷系統中蓄冰槽和蓄冰球的結構與性能,對蓄冷過程進行了實驗測試,并將測試結果與理論計算進行了對比分析,提出了優化冰球式蓄冷系統的方法.

冰球式封裝蓄冰槽;傳熱計算;蓄冷過程;實驗研究

冰蓄冷空調系統以其“削峰填谷”的優勢,在國內外日益得到高度重視和廣泛應用[1].冰蓄冷空調系統分靜態與動態制冰,靜態制冰中又以盤管式和冰球式為主,相對盤管式系統,冰球式蓄冷系統結構簡單可靠、蓄冷量大、冰球外殼耐腐蝕、壽命長、阻力小、故障率低、融冰速率快,亦能實現大溫差的低溫送風,適用于各種集中式空調系統[2-3],因此,掌握該蓄冷設備的蓄冷特性對于工程應用非常重要.

本文設計搭建了一種冰球式封裝蓄冷系統,通過對蓄冰槽內的蓄冷過程進行傳熱計算,得到了蓄冰槽蓄冷過程中乙二醇溶液及蓄冰球的溫度變化規律.根據實驗測試與理論計算值的對比分析,提出了優化冰球式蓄冷系統的結構與傳熱的設計方法.

1 蓄冰槽蓄冷過程理論分析

1.1 蓄冷過程傳熱分析

蓄冰槽內的蓄冷過程是一個非穩態的傳熱過程[4-5],主要包括載冷劑與冰球外部表面之間的對流換熱、冰球球殼的導熱、冰球內固相冰層(液相水層)的導熱這3個部分.在蓄冷過程中,載冷劑從蓄冰槽底部流入,在冰球之間的縫隙通道內流動,與冰球內的水進行熱交換,載冷劑不斷從冰球內吸收熱量,溫度上升;同時,冰球內水溫隨著蓄冷時間的推移不斷下降,冰球內的水逐漸結冰,冰層不斷加厚,整個過程的傳熱系數隨時間發生變化,因此,蓄冷是一個非穩態的傳熱過程.

蓄冷過程分為3個階段:第一階段為冰球內水的顯熱蓄冷階段,此時,冷量以水的顯熱形式儲存,直至水溫下降到0℃;第二階段以冰的潛熱蓄冷為主,在此過程中,冰球內水溫繼續下降,冰球內開始結冰,過程如圖1所示,冰層首先從冰球下部形成,逐漸向內向上移動,冰層逐漸變厚,熱阻增加,結冰速率愈來愈慢,最后在上部封頂;第三階段是冰球內冰的顯熱蓄冷過程,此時,冰球內的水全部凍結成冰,溫度繼續下降,直至蓄冷結束.

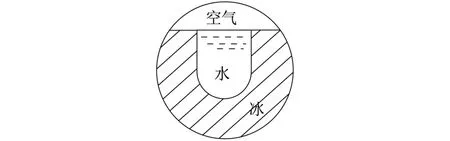
圖1 冰球的結冰過程Fig.1 Freezing process of the ice ball

1.2 蓄冷過程傳熱計算

為了簡化計算,假設:a.蓄冷時,冰球在蓄冰槽內均勻分布,載冷劑在蓄冰槽內自下而上均勻地掠過冰球,與冰球內的水進行熱交換;b.冰球內充滿水,且冰球內的水降至-2℃開始結冰;c.蓄冰槽保溫性能良好,與周圍環境之間不存在換熱.簡化后的蓄冷單元體如圖2所示.

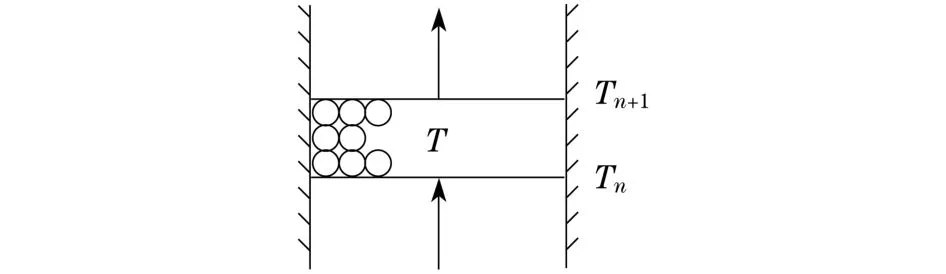
圖2 蓄冷單元體示意圖Fig.2 Schematic diagram of the storage unit

從圖2中可以看出,蓄冰槽進、出口格柵之間分成n個蓄冷單元[6].在不考慮傳熱損失的情況下,蓄冷過程中乙二醇溶液的吸熱量應等于冰球的蓄冷量.以第n層為研究對象,單位時間內蓄冷單元體的能量變化等于乙二醇溶液與球內水的熱交換量,即

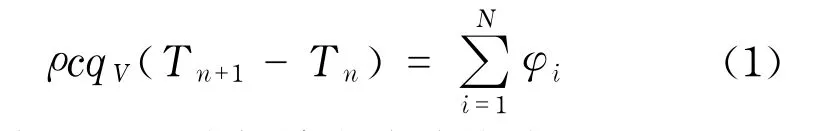
式中,φi表示乙二醇與單個冰球換熱量,kW;ρ,c為乙二醇密度和比熱容,kg/m3,kJ/(kg·℃);q V為乙二醇流量,m3/s;Tn,Tn+1為乙二醇進、出蓄冷單元體溫度,℃;T為蓄冷單元體進、出口平均溫度;N表示每層冰球的個數.

單個冰球的換熱量取決于蓄冷介質的狀態,冰球凝固過程分為水冷卻階段、成核階段、冰層生長階段和冰降溫階段[7-10],凝固過程如圖3所示.S為固相蓄冷介質,L為液相蓄冷介質,re為冰球的外徑,ri為冰球的內徑,rc,τ為冰層的半徑.

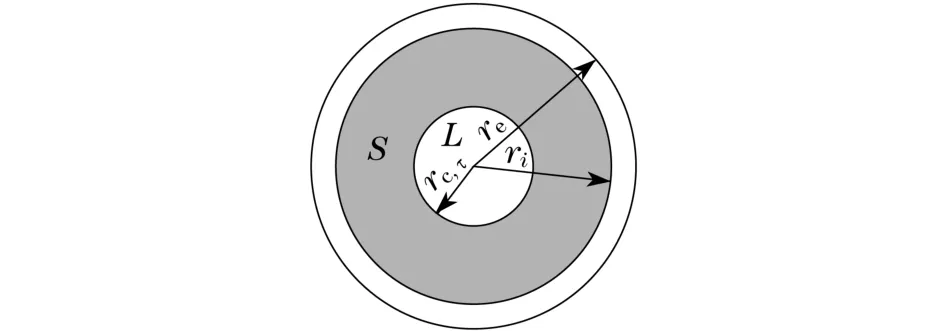
圖3 冰球內的凝固過程Fig.3 Solidification process of the ice ball

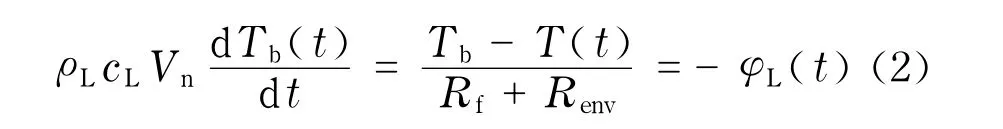
式中,φL(t)表示水冷卻階段的換熱量,kW;ρL為冰球內水的液相密度,kg/m3;cL為冰球內水的比熱容,kJ/(kg·℃);Vn為冰球內水的體積,m3;Rf為乙二醇與冰球外部表面之間的熱阻,m2·℃/kW; Renv為球殼的熱阻,m2·℃/kW;Tb為冰球內水的溫度,℃;T(t)為乙二醇溶液的溫度,以單元體進出口平均值計,(Tn+1+Tn)/2.

b.成核階段.

現對不同階段冰球的換熱量進行分析.

a.水冷卻階段.

在液態水冷卻階段,冰球的換熱以導熱和對流為主,單位時間內的換熱量

當冰球中的液態水冷卻到過冷溫度(-2℃)后,蓄冷進入成核階段,冰晶在過冷水中逐漸形成和生長,形成冰晶后的水溫逐步回升到凝固溫度0℃.成核階段屬于亞穩態,一旦亞穩態遭到破壞,冰層就開始在球的內表面形成,并逐步向內擴展,直到rc,τ(t)=0,結冰過程完成.

成核完成時的凝固薄冰層半徑

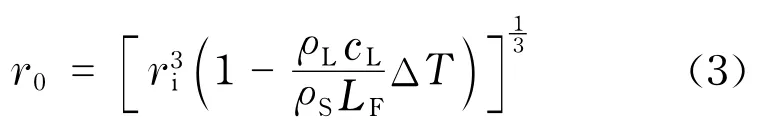
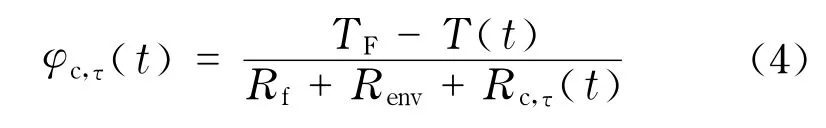
式中,φc,τ(t)表示冰層生長階段的換熱量,kW;TF為冰的凝固溫度,℃;Rc,τ(t)為固相冰層的熱阻, m2·℃/kW.

式(4)中的熱阻可分別按下式計算:

式中,ρS為冰球內水的固相密度,kg/m3;LF為蓄冷介質的凝固熱,kJ/kg;ΔT為水的過冷度,℃.

c.冰層生長階段.

冰層的生長階段以冰球內的水開始結冰為起始時刻τ,直到結冰完成時刻tf,τ.載冷劑與冰球的換熱量

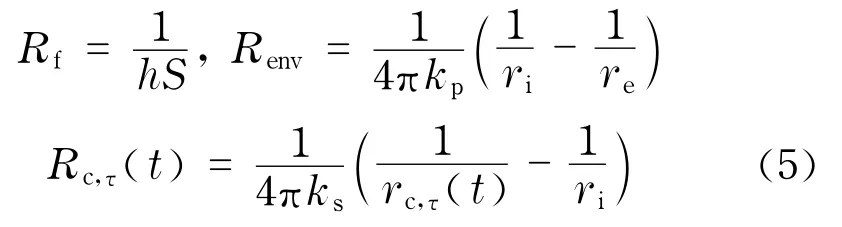
式中,h為乙二醇與冰球表面之間的表面傳熱系數, kW/(m2·℃);S為冰球的外表面積,m2;kp為球殼的導熱率,kW/(m·℃);ks為冰的導熱率, kW/(m·℃).

乙二醇與冰球表面間的傳熱系數h按下式確定:

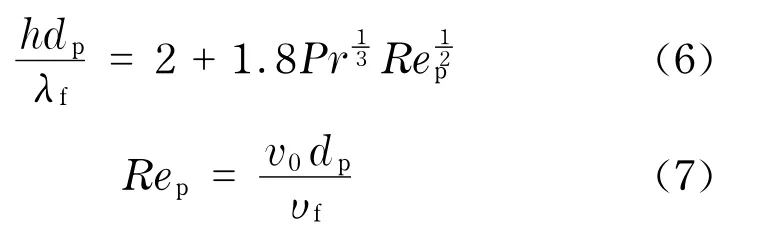
式中,dp為冰球直徑,m;λf為乙二醇導熱系數, W/(m·℃);Pr為乙二醇的普朗特數;Rep為乙二醇流經冰球時的雷諾數;v0為乙二醇的速度,m/s; υf為乙二醇的運動粘度,m2/s.

冰層半徑rc,τ(t)的計算公式為

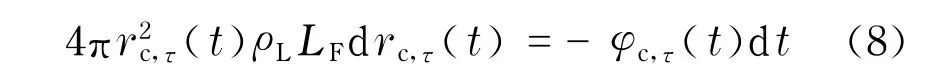
當t=τ時,則有rc,τ(τ)=r0;當t=tf,τ時(凝固過程完成),rc,τ(tf,τ)=0.tf,τ為冰球凝固完成時刻.利用式(3)～(8)就可確定φc,τ(t).

d.冰的降溫階段.

在冰的降溫階段,冰球內的水已完全凝固,冰不斷釋放顯熱,該階段的換熱方式與水冷卻階段相似,因此,冰球的換熱量φS按式(2)計算,只需將ρL,φL替換為ρS,φS即可.

通過上述公式,根據各個階段τ和t值,則有φi=φL,φc,τ=φS,從而計算出蓄冰槽內乙二醇溶液及冰球內溫度隨時間的變化趨勢.

2 蓄冰槽蓄冷過程實驗研究

2.1 蓄冷實驗系統

實驗蓄冷系統共分為3個回路,其原理圖如圖4所示(見下頁).紅色代表制冷機組的制冷循環回路,藍色代表蓄冰裝置乙二醇溶液的蓄冷、釋冷循環回路,黑色代表冷媒水循環回路.

實驗系統采用雙工況制冷機組,設置兩套并聯膨脹閥,使機組能夠在空調或蓄冷工況下正常工作.空調工況制冷機的蒸發溫度為0℃,蓄冷工況制冷機的蒸發溫度為-10℃,既可向常規空調系統提供7℃的冷媒水,也可為蓄冰槽提供-6℃的乙二醇溶液.蓄冷系統采用部分蓄冷的運行模式,制冷機組和蓄冰槽串聯,機組位于蓄冰槽上游,載冷劑先流經制冷機組降溫后再流過蓄冰槽,其優點是制冷機組的蒸發溫度較高,可提高機組的運行效率.

2.2 蓄冰槽的設計

由于空調房間面積為120 m2,因此,該實驗系統是一種小型冰蓄冷系統.根據安裝位置的不同,蓄冰槽可選用臥式和立式兩種結構,為避免載冷劑流動短路而引起換熱性能下降的現象,蓄冰槽選擇立式結構.由于受到房間層高的限制,蓄冰槽高度的設計首先要保證載冷劑能夠在蓄冰槽內達到設計要求的換熱效果,綜合考慮房間的凈高、管道設備所占空間等因素,蓄冰槽有效高度設計為1.2 m,有效容積為0.96 m3.蓄冰槽的蓄冷量為40 kW·h,蓄冷時間為8 h,承擔約40%的空調負荷.

載冷劑采用質量分數為25%的乙二醇溶液,其凝固溫度為-10.7℃[11].乙二醇溶液進蓄冰槽的溫度需合理設計.蓄冷溫度太高,不能達到冰球結冰時的過冷度.蓄冷溫度太低,一方面導致機組的蒸發溫度下降,制冷系數降低;另一方面是溫度過低,乙二醇接近凝固點,不利于系統的正常運行.綜合考慮乙二醇溶液進蓄冰槽的最低溫度為-6℃,進、出口溫差為2.5℃.

圖4 冰蓄冷系統原理圖Fig.4 Diagram of the ice storage system

2.3 蓄冰球的選擇

冰球選用美國CRYOGEL高密度聚乙烯材料蓄冰球,直徑約103 mm,壁厚2 mm,冰球表面設有16個凹坑,凹坑的直徑為25.4 mm.水結成冰時凹坑向外突出容納膨脹的量;冰融化時,每個球又恢復到原來的形狀,冰球結冰前后的外形變化如圖5所示.冰球中幾乎不含空氣,有效換熱面積大,換熱效率高,單位立方米堆放體積的蓄冷量可達到62.6 kW·h.冰球中添加AgI膠體成核劑,降低了結冰過冷度,加快了結冰和融冰速度,提高了結冰的溫度.冰球均勻地擺放在蓄冰槽內,共計1 000個冰球.

2.4 實驗測試儀器配置

蓄冰槽內乙二醇溶液溫度采用T型熱電偶進行測試,等級為I級,偏差為±0.5℃,測溫范圍為-50～+50℃.蓄冰槽沿高度方向被分為5層,每層沿寬度方向均勻布置4個T型熱電偶.冰球內溫度采用PT100鉑電阻進行測試,精度等級為A級,偏差為±0.1℃.鉑電阻探頭放入冰球中心處,實驗過程中共測試3個冰球的溫度變化,在距蓄冰槽底層1 m的位置,將被測試冰球沿寬度方向均勻放置.

乙二醇溶液流量采用渦街式流量傳感器進行測試,精度等級為1.0級,工作壓力小于等于1.6 MPa,溫度范圍為-40～150℃.

實驗數據由數據采集儀配合Labview數據采集程序進行采集,將采集的數據輸入電腦進行數據分析.

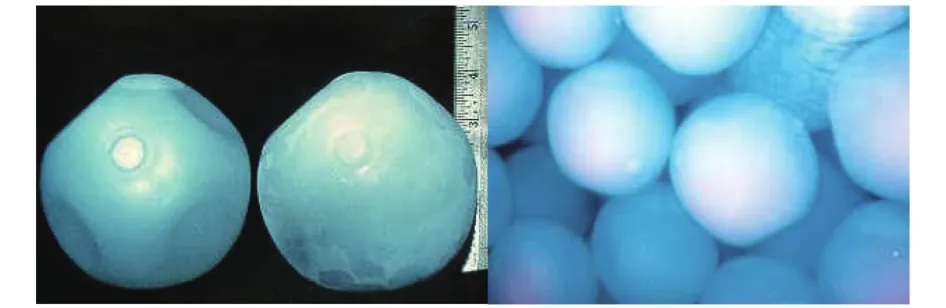
圖5 單個與多個冰球結冰前后的外形變化Fig.5 Changes in shape before and after the freezing of single and multiple ice balls

2.5 實驗結果及分析

在乙二醇溶液初始溫度為20℃,流量為3.0 m3/h的情況下進行蓄冷實驗,結果如圖6所示.

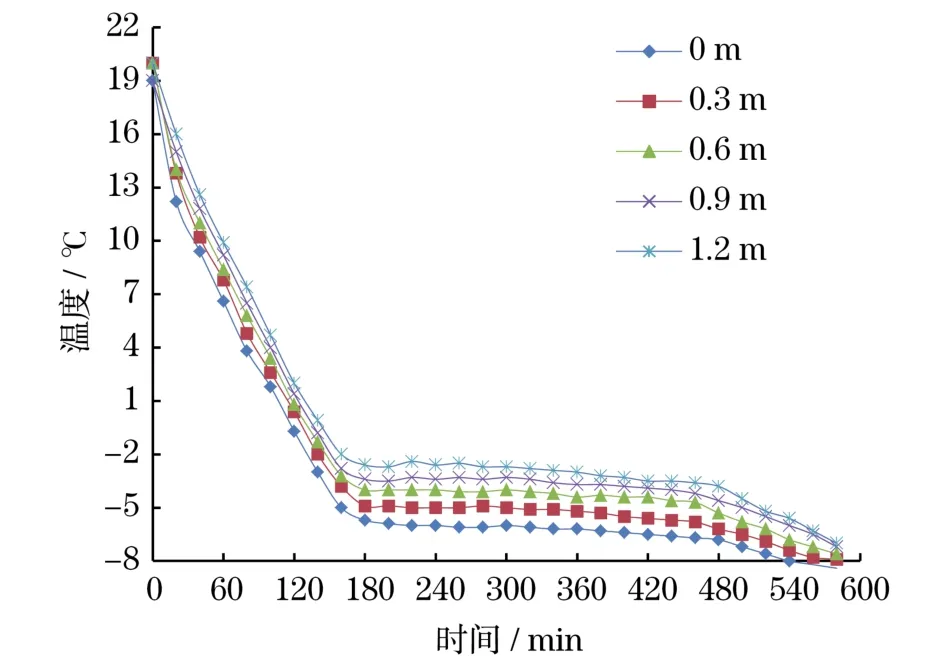
圖6 蓄冰槽內各層乙二醇溶液溫度隨時間的變化Fig.6 Temperature changes with time of each layer glycol solution in the storage tank

從圖6可以看出,在蓄冷開始階段(前180 min左右),乙二醇溶液的溫度下降較快,冰球內的水處于顯熱蓄冷階段.當乙二醇溫度降至-4℃后,溫度下降速率開始變化緩慢,此時冰球內的水進入相變階段,結冰過程開始.當冰球內的水完全結冰時(480 min左右),乙二醇溶液的溫度又開始快速下降,冰球內的冰處于顯熱蓄冷階段.最后溶液在蓄冰槽的進、出口溫度基本趨于一致,蓄冷過程結束.

從圖7可以看出,在相同條件下,蓄冰槽出口實測溫度與計算溫度基本一致.在整個過程中,實測溫度比理論計算溫度略高,主要是由于蓄冰槽與周圍環境之間存在換熱以及實驗過程中測量儀器存在誤差所致.

從圖8可以看出,冰球溫度變化與乙二醇溫度變化趨勢相同.蓄冷過程進行到180 min左右時,冰球內的水溫趨于過冷溫度,冰球內的水開始在壁面處結冰,此時的蓄冷既有顯熱蓄冷也有潛熱蓄冷,當全部水溫回升到0℃時,冰球完全進入相變階段.在相變階段,實測溫度與理論計算溫度的誤差在10%以內,存在誤差的主要原因是結冰時測點附近有水的存在,導致實測溫度比計算溫度略低.

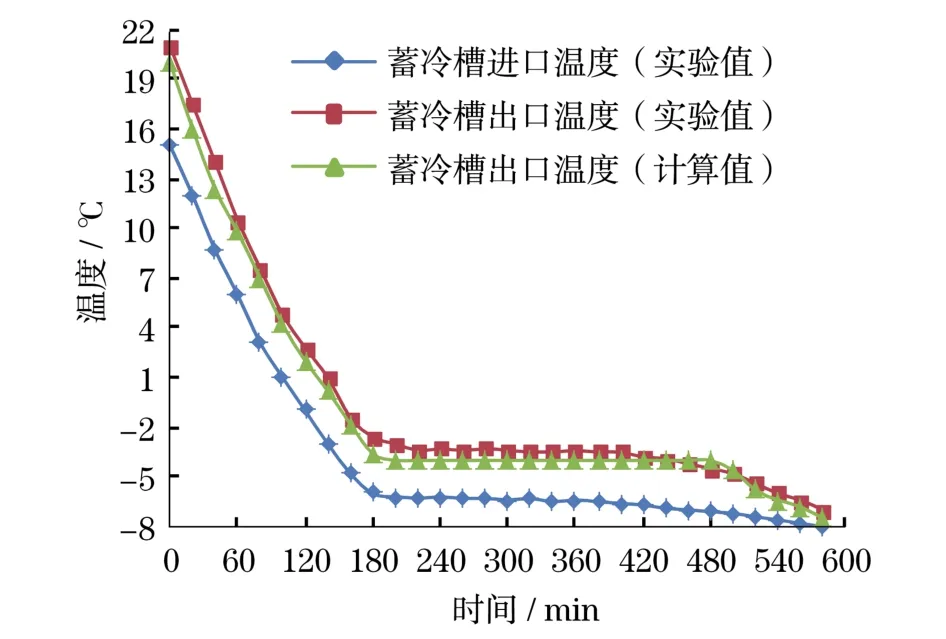
圖7 蓄冰槽乙二醇溶液出口溫度隨時間的變化Fig.7 Outlet temperature changes with time of glycol solution in the storage tank

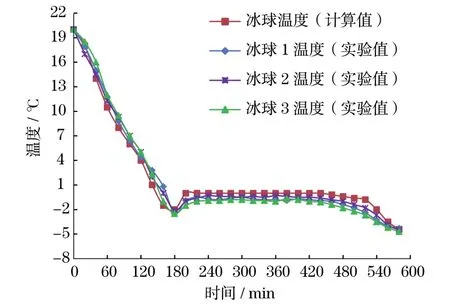
圖8 不同冰球內水溫隨時間的變化Fig.8 Temperature changes with time of the ice ball

從圖9可以看出,顯熱階段(前180 min左右)由于乙二醇溶液溫度的快速下降,蒸發溫度下降趨勢也較大.潛熱蓄冷階段,由于水的相變溫度不變,導致乙二醇溶液溫度基本保持不變,蒸發溫度也基本不變,系統的運行維持在相對穩定的狀態.蓄冷時間經過480 min左右時,蒸發溫度又開始下降,表明冰球內的水完全結冰,蓄冷過程基本結束.

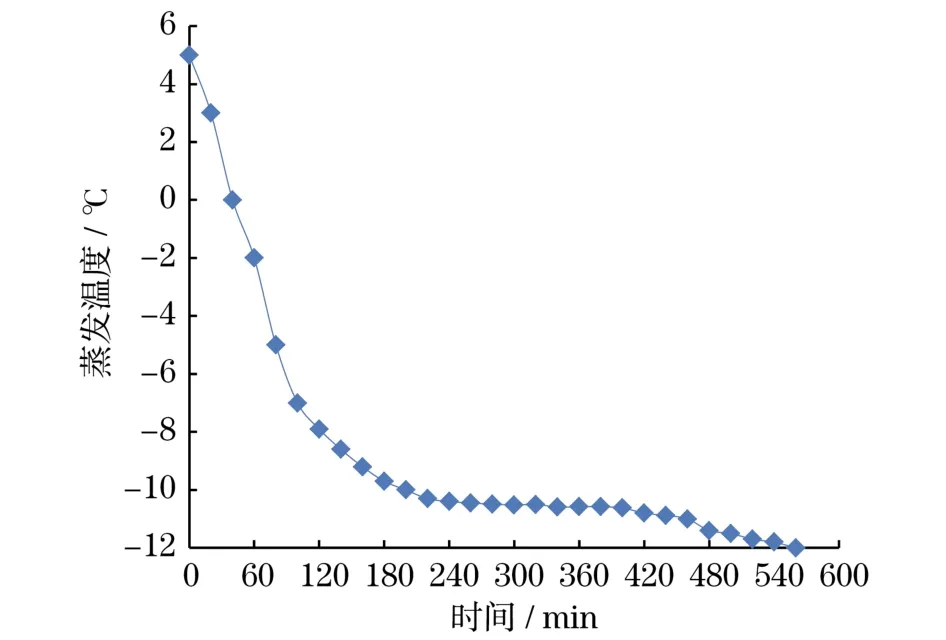
圖9 機組蒸發溫度隨時間的變化Fig.9 Evaporation temperature changes with time of the unit

3 結 論

a.針對冰球式封裝蓄冰槽的蓄冷過程進行了理論與實驗研究,通過理論計算與實驗測試得到了蓄冷過程中乙二醇溶液及冰球的溫度變化規律,理論計算與實測結果基本吻合.

b.在蓄冷過程中,當蓄冰槽載冷劑出口溫度趨于穩定,并接近進口溫度時,說明蓄冷過程結束,因此,可通過控制載冷劑出口溫度來調節蓄冷時制冷機組的運行工況.

c.在蓄冷過程中,相變潛熱蓄冷量占整個蓄冷量的81%,因此,在蓄冷系統設計時應選擇相變潛熱大的材料作為蓄冷介質,以減小蓄冷系統的體積.

d.冰蓄冷系統由于相變溫度低于常規空調系統供冷溫度,且蓄冷時存在較大的過冷度,使得制冷機組蒸發溫度降低,機組效率下降,耗電量增加,因此,蓄冷過程中可通過在冰球中添加成核劑減小水的過冷度的方法,提高機組效率,同時考慮采用低溫送風空調系統,達到提高整個空調系統效率的目的.

[1] 張永銓.我國蓄冷技術的發展[J].暖通空調,2010,40(6):2-5.

[2] 殷平.冰蓄冷低溫送風系統設計方法(1):室內計算參數、舒適感、室內空氣品質[J].暖通空調,2004,34 (5):59-65.

[3] 周文鑄,劉道平,殷亮,等.多功能蓄冷空調實驗裝置的研制和應用[J].上海理工大學學報,1998,20(1): 97-102.

[4] 杜艷利,何世輝,肖睿,等.直接蒸發內融式冰蓄冷空調的蓄冷和釋冷特性[J].制冷學報,2007,28(3):33-35.

[5] 張華.冰球蓄冷罐蓄冷過程的動態特性[J].真空與低溫,2000,12(4):211-224.

[6] 方貴銀.蓄能空調技術[M].北京:機械工業出版社, 2006.

[7] 羅森諾W M.傳熱學應用手冊[M].齊欣,譯.北京:科學出版社,1992.

[8] Bédécarrats J P,Strub F,Falcon B,et al.Phase-change thermal-energy storage using spherical capsules: performance of a test plant[J].International Journal of Refrigeration,1996,19(3):187-196.

[9] Ismail K A R,Henriiquez J R,da Silva T M A. Parametric study on ice formation inside a spherical capsule[J].International Journal of Thermal Science, 2003,42(9):881-887.

[10] Brian Silvetti P E.Application fundamentals of icebased thermal storage[J].ASHRAE Journal,2002,44 (2):30-35.

[11] 王瑾,沈小彬,梁志,等.冰蓄冷空調系統中乙二醇的緩蝕劑研究[J].上海理工大學學報,2014,36(2): 181-184.

(編輯:石 瑛)

Theoretical Analysis and Experimental Study on Charging Process of Ice Hockey Style Packaged Storage Tank

WANGJin1, ZHAOKai1, WANGSuying2, ZHAOLuping1, DUANWenshan1
(1.School of Environment and Architecture,University of Shanghai for Science and Technology,Shanghai 200093,China; 2.College of Information and Business,Zhongyuan University of Technology,Zhengzhou 450000,China)

The charging process of ice hockey style packaged storage tank was analyzed and a numerical heat transfer equation was established,Through the theoretical calculation for charging process,the temperature changes of glycol solution and ice ball were obtained.A bench for the tests of hockey style storage air conditioning system was established,the structure and performance of the storage tank and ice ball were analyzed,and the experimental tests on charging process were carried out,The test results were compared with the theoretical calculation results,and the optimization of ice storage system were put forward.

ice hockey style packaged storage tank;heat transfer calculation;charging process;experimental study

TU 831.5

A

1007-6735(2015)03-0263-06

10.13255/j.cnki.jusst.2015.03.011

2014-05-09

上海市教委重點學科資助項目(J50502)

王 瑾(1955-),女,教授.研究方向:制冷空調工程研發與節能.E-mail:wjljh2003@163.com