Padé近似下模擬一般色散媒質的FDTD改進方案

劉廣東

·物理電子學·

Padé近似下模擬一般色散媒質的FDTD改進方案

劉廣東

(阜陽師范學院物理與電子工程學院 安微 阜陽 236037)

為了方便模擬不同媒質的色散特性，提出了一種時域有限差分(FDTD)改進方案，適用于統一處理幾類各向同性、線性、有磁電色散媒質的電波傳播問題：媒質類型可以是Havriliak-Negami(H-N)媒質、Davidson-Cole(D-C)媒質、Cole-Cole(C-C)媒質、Debye媒質、常規(非色散)媒質或其任意組合；媒質屬性可以是單極或多極的、有電耗的或無電耗的。該方案利用帕德(Padé)近似法，導出了一組整數階的輔助微分方程(ADEs)，既克服了其中分數階導數的主要困難，又展現了通用性好、復雜度低的優勢。通過對一維及三維算例解析、數值結果之間的對比，初步證實了改進方案的可行性和有效性。

輔助微分方程; 時域有限差分法; 色散媒質; 帕德近似法

實驗測量證實：生物組織、大地、巖石、水、液晶、聚合物材料等眾多媒質的電參數展現了頻率相關性(這些媒質稱作電色散媒質)；不同媒質還可能展現不同的電色散特性[1-2]。至今已提出好幾種經驗模型以描述不同的電色散特性，一般可概括為兩大類型[3]：第一大類主要有Debye模型[4](如人體組織、等離子體、土壤)、Drude模型[5](如等離子體、金屬)和Lorentz模型[2](如光學材料、人工介質)，其共性在于：媒質的(復)介電常數是jω(j表示虛數單位，ω表示角頻率)整數次冪的函數[3]；第二大類主要包含Cole-Cole(C-C)模型[6-8](如生物組織、高分子材料)、Davidson-Cole(D-C)模型[3](如甘油、丙二醇)和Havriliak-Negami(H-N)模型[9](如聚合物)，其共性在于：媒質的(復)介電常數是jω分數次冪的函數[3]。后文將以不同媒質對應的色散模型(或所屬大類)命名以區分不同的媒質類型(如稱色散特性滿足C-C模型的媒質為C-C媒質)。

近幾年來，由于媒質的色散特性引起了較多關注[10-11]，相應地，FDTD法的解算對象已由常規的非色散媒質[12]拓展到色散媒質[6,13]。

FDTD建模第一大類(Debye、Drude、Lorentz)媒質，已發展了多種方法，主要有3種思路：1) 引入ADE[2,7-9]；2) 利用遞歸卷積(recursive convolution, RC)[2,13]；3) 定義移位算子(shift operator, SO)[2,14]。

然而，FDTD建模第二大類(C-C、D-C、H-N)媒質，仍是當前的難點之一，其主要困難是差分實現分數階導數[3]。對此，文獻[15]進行了一系列開創性的基礎工作：利用帕德(Padé)近似法，導出了一組整數階ADEs，克服了分數階導數困難，分別提出了處理(無磁、線性、各向同性的)單極、多極C-C媒質[7-8]、單極D-C媒質[3]和單極H-N媒質[9]的FDTD方案；一維的系列仿真結果初步證實了這些方案的可行性[7-9]。文獻[6]給出了建模多極C-C媒質的FDTD改進方案和三維的仿真測試。

為了增加通用性和降低復雜度，方便統一編程處理不同類型色散媒質的電波傳播問題，本文主要以文獻[7-9]為基礎，提出了一種FDTD改進方案，創新(改進)之處主要體現在：1) 從單極色散媒質推廣到多極情形；2) 從無磁媒質推廣到有磁情形；3) 增加了靜態電導率項；4) 增加了三維數值算例檢驗該方案的性能和精度。

1 問題描述

首先給出后文滿足的假設條件和必要的符號說明：1) 假設所研究的色散媒質是各向同性、線性、有磁和電色散的，該假設條件經常應用于地球物理勘探、微波醫學成像、紅外與毫米波技術等領域[1-5]；2) 符號頂部加點表示其值為復數。

若問題空間r處存在一般的(同時存在電極化損耗和歐姆損耗)多極H-N媒質，則頻域本構關系為：

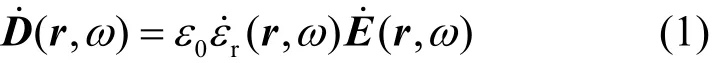
式中，D˙和E˙分別表示電位移矢量和電場強度矢量；ω = 2πf，f為頻率；ε0為真空介電常數；多極H-N媒質的相對介電常數定義為[16]：

式中，ε∞為光學相對介電常數；σs為靜態電導率；Δεw= εs,w?ε∞；εs,w為第w極的靜態相對介電常數；W為極總數；第w極的復值因子wf˙為：

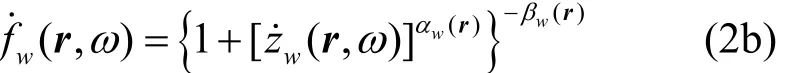
式中，αw(0≤αw≤1)；βw(0≤βw≤1)為第w極色散參數；wz˙= jωτw(r)；τw表示第w極的弛豫時間。

本文采用的色散模型是較為通用的形式：1) 當 W = 1時，簡化為單極情形；2) 當W = 1且αs= 0時，簡化為文獻[9]的式(1)；3) 如果W = 1、αw= 1且σs= 0時，退化為文獻[3]的式(1)；4) 如果βw= 1且σs= 0時，退化為文獻[8]的式(1)；5) 如果W = 1、βw= 1且σs= 0時，變為文獻[7]的式(1)；6) 如果αw= 1且βw= 1時，變為Debye模型[4]；7) 假如αw= 1、βw= 1且Δεw= 0時，轉化為非色散情形。

2 輔助微分方程(ADEs)

為了克服FDTD方案中分數(αw、βw一般為分數)階導數的困難，首先，借鑒文獻[7-9]的研究思路，利用帕德(Padé)近似法[15]，并由wf˙在wz˙= 1處解析，將wf˙近似為：

式中，N、M分別表示分子、分母多項式的階數；pn、qm分別表示分子、分母多項式的系數，可通過求解線性方程組獲得，相關細節參見文獻[7-9]。

將式(3a)代入式(2a)，易得相對介電常數的帕德近似值為：

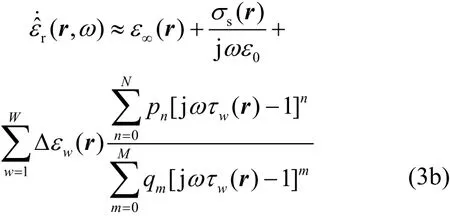
這樣，相對介電常數已全部轉化為jω整數次冪的函數，有利于后文FDTD方案的討論。

其次，定義第w極(輔助的)頻域電極化強度矢量為：

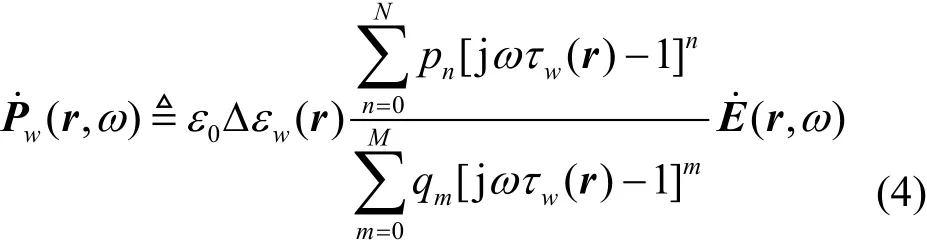
最后，應用傅里葉逆變換(inverse Fourier transform, IFT)，可以得到一組(W個)關于時域電極化強度矢量Pw的ADEs為：

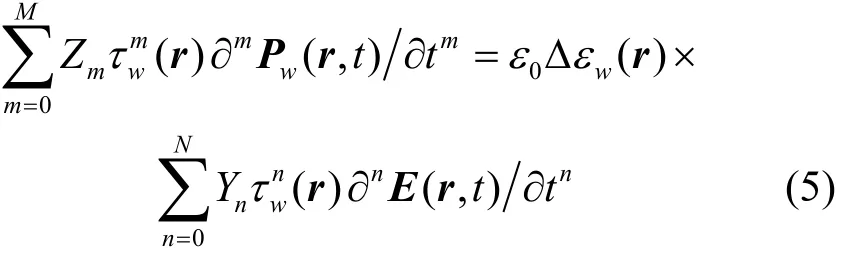
其中：

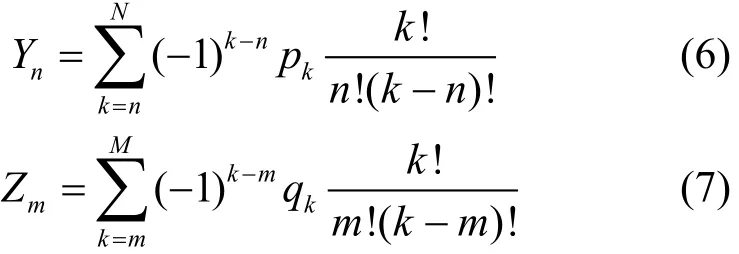
式中，E表示時域電場強度矢量；t表示時間。至此，這組輔助微分方程由于包含了整數階的時間導數，可以方便地通過有限差分法實現時間的離散化。

3 時域有限差分方案

前述電色散媒質中，時域(微分形式)的麥克斯韋(Maxwell)方程組為[8]：

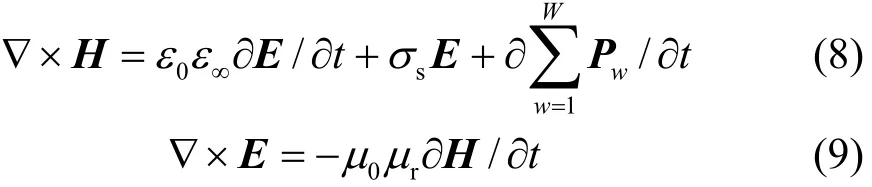
式中，H(為了表達簡潔，省略了自變量，下文同)表示磁場強度矢量H(r,t)；μr表示相對磁導率，當μr= 1時，媒質簡化為文獻[7-9]的無磁特例。

在t=iΔt(i和Δt分別表示時間步的指標和步長)時刻的電場強度矢量Ei，其n階的時間偏導數可通過中心差分近似為[7-9]：

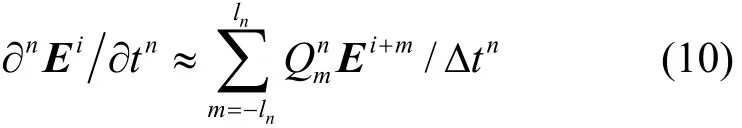
式中，l=n/2表示對n/2上取整；Qnm為中心差分參數[6-9]；Pw的中心差分近似可類似地獲得。至此，就實現了式(5)的FDTD時間離散化。

文獻[9]顯示，欲使FDTD方案穩定，需滿足N≤M。為了簡化描述，假定M = N(其原因后文給出)，則有lM=lN。進一步假定已知iΔt時刻的Pw、E和(i+0.5)Δt時刻的H，分別差分式(8)～式(9)，并引入輔助矢量Φw[8]，經過整理，多極H-N媒質的FDTD時間迭代步進方案可簡述如下：

1) 計算輔助矢量為：

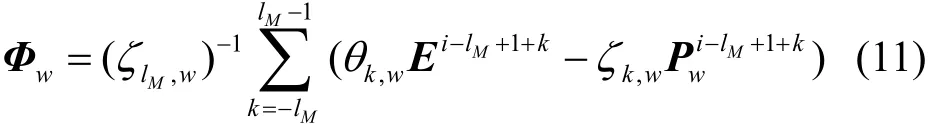
其中：

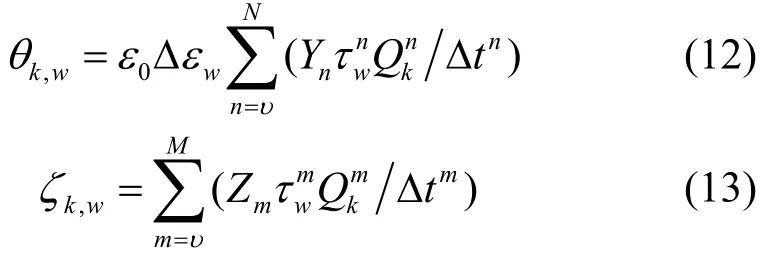
式中，k = ?lM,?lM+1,…,lM；ν = max{2|k|?1,0}。

2) 更新(i+1)Δt時刻的電場強度矢量為：

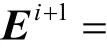
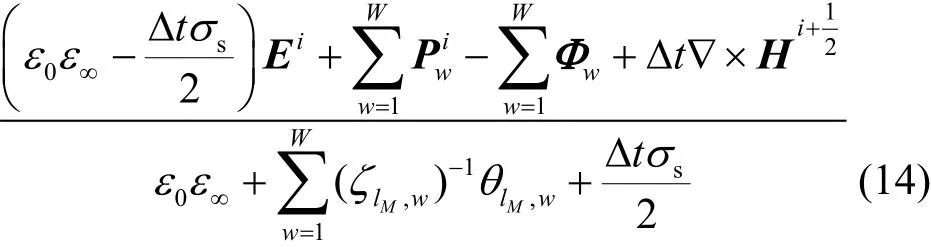
3) 更新(i+1)Δt時刻的電極化強度矢量為：

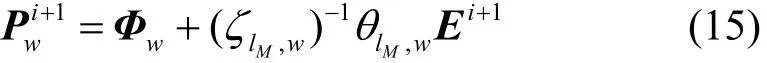
4) 更新(i+1.5)Δt時刻的磁場強度矢量為：

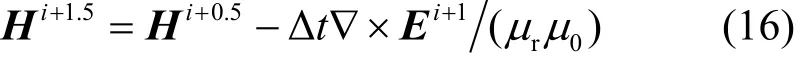
前述FDTD方案中，對于每個離散的網格，每個場分量的存儲量為M(W+1)+W，磁場以外的計算時間(乘法運算次數)為(2M+1)W+3，當W=1時與文獻[9]的結果相同。

該FDTD方案的時間迭代步進流程(技術路線)如圖1所示[6]。

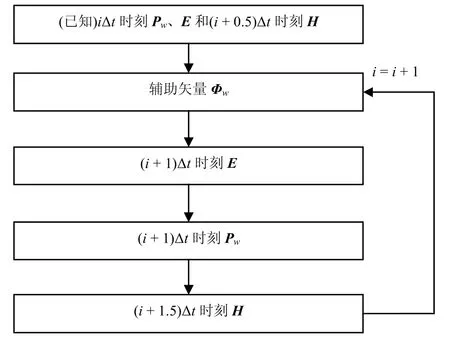
圖1 FDTD時間迭代步進流程圖

4 結果與討論

由于前述FDTD方案中采用了帕德(Padé)近似，下面首先檢驗帕德近似的精度。

4.1 帕德近似的精度

定義帕德近似的相對均方(relative mean square, RMS)誤差為[3,7]：

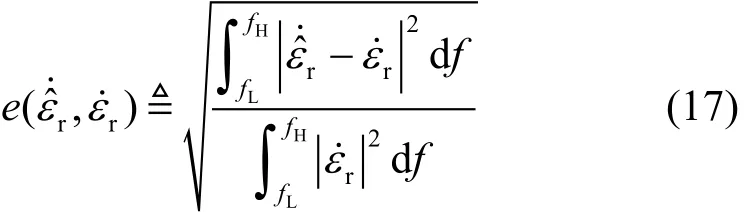
式中，媒質相對介電常數的解析值ε˙r和Padé近似值ε˙?r可分別通過式(2a)和式(3b)求得；fH、fL分別表示上、下限頻率。

算例 1 以文獻[9]中的均勻單極H-N媒質(聚丙烯酸正辛酯，聚丙烯酸的一種衍生物)為測試目標，各模型參數分別為W = 1、ε∞= 2.61、σs= 0.001 S/m、εs,1= 3.88、τ1= 39.98 ps、α1= 0.73、β1= 0.66。上、下限頻率分別取為fH= 100 GHz、fL= 10 MHz，分母多項式的階數取為M = 3,4,…,10，分子多項式階數分別取為N = M、N = M?1和N = M?2時，帕德近似的相對均方誤差e隨M的變化關系如圖2所示(誤差軸為對數坐標，后文同)，其中當M=3、4、5、6時，本文的誤差與文獻[9]的誤差對比如表1所示。

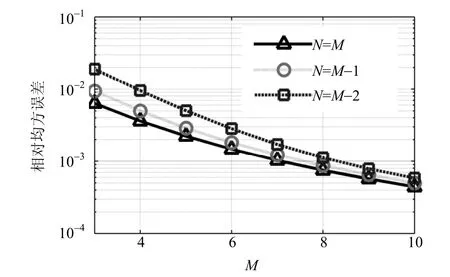
圖2 算例1相對均方誤差隨M的變化關系

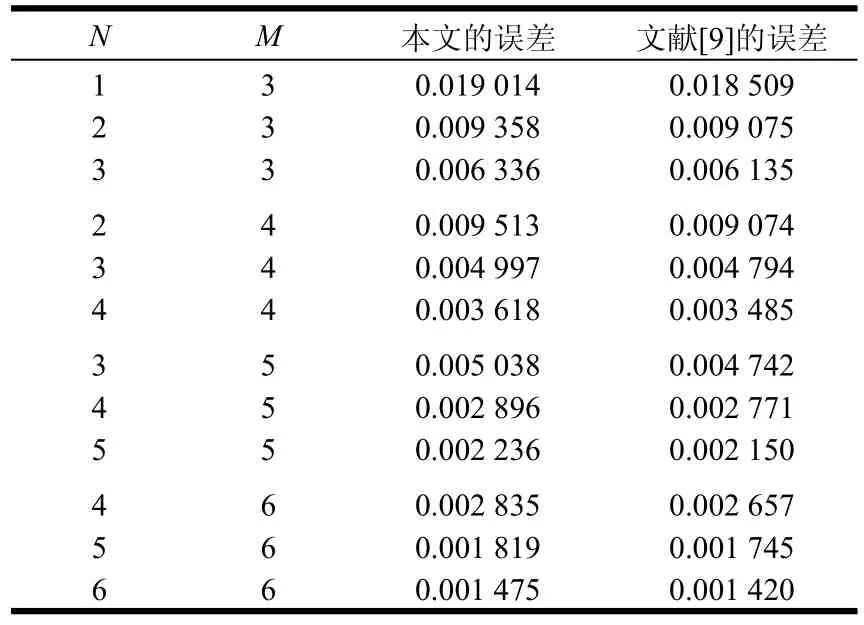
表1 相對均方誤差隨N、M的變化關系

分析圖2發現：1) 當M相同時，在N = M、N = M?1、N = M?2的3種情形下，第一種情形誤差最小，這正是前文討論FDTD時間步進方案時選取N = M的依據；2) 在N = M、N = M?1、N = M?2的3種情形下，隨著M的增加，誤差均逐漸減小(然而，實現FDTD方案所需的存儲量M(W+1)+W和計算時間(2M+1)W+3也同時增加，建議折中選擇M、N)。

結合表1可知：1) 在表中所列舉的12種情形下，本文的誤差均略大于文獻[9]的誤差(適當增加離散頻點數可使二者相當)，因此，文獻[9]的單極情形可視為本文改進方案的一個特例；2) 當N = M = 4時，本文的誤差約為0.003 6，不僅計算精度能被一般的工程應用所接受，而且計算速度比較適中。

算例 2 (為不失一般性)選取一種2極(即W=2)的均勻H-N媒質為測試目標，其余模型參數分別為ε∞= 2.61、σs= 0.01 S/m、εs,1= 3.88、εs,2= 3.50、τ1= 39.98 ps、τ2= 29.98 ns、α1= 0.73、α2= 0.80、β1= 0.66、β2= 0.70。頻率上、下限及多項式的階數均與算例1相同，相對均方誤差e隨M的變化關系如圖3所示。

由圖3可見：對于多極H-N媒質，也有類似于算例1(單極情形)的結果，只是誤差略微增加。當N = M = 4時，相對均方誤差約為0.004 3，還能滿足一般的工程應用需求，因此，在后文的FDTD方案中，多項式的階數也默認這組取值。4.2 FDTD方案的可行性

圖3 算例2相對均方誤差隨M的變化關系

為了檢驗前述FDTD改進方案的可行性，再給出兩個算例，選擇算例基于以下考慮：1) 問題空間涵蓋不同物理維度；2) 色散媒質涵蓋不同類型；3) 媒質涵蓋不同極數；4) 色散模型參數涵蓋文獻作者自擬和真實測量；5) 測試采用不同類型目標參數。

算例 3 出自文獻[3]的一維問題：單極均勻無磁D-C媒質(媒質參數分別為W = 1、μr= 1、ε∞= 2、σs= 0 S/m、εs,1= 50、τ1= 153 ps、β1= 0.9和α1= 1.0)充滿z≥0半空間，其余空間為真空；一列入射平面波(電場沿x方向極化)沿+z方向傳播，平面波由下述的超寬帶(ultra-wideband, UWB)調制高斯脈沖源s激勵產生[3]：

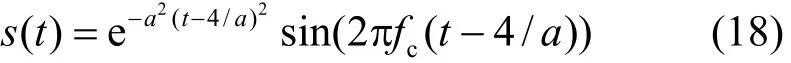
式中，參數a =1.26×1010s?1，中心頻率fc= 6 GHz，該脈沖的頻譜主要涵蓋0.1～10 GHz頻率范圍。

FDTD離散化的空間、時間步長分別取為Δz = 1.1 mm、Δt = 1.5 ps，離散網格數、時間步數分別取為nz= 200、nt= 3 000。仿真區域?z一側采用簡單的吸收邊界：Ex(zmax, t+Δt) = Ex(zmax?Δz, t)，其中zmax表示對應的邊界位置坐標。

記z、z+d分別表示D-C媒質中的兩個不同位置，FDTD仿真并且存儲這兩處的時域電場Ex(z, t)、Ex(z+d, t)，后處理(傅里葉變換)獲得相應的頻域電場E˙x(z, ω)、E˙x(z+d, ω)，則色散媒質相對介電常數的FDTD估計值為[3,7]：

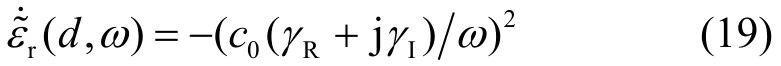
式中，c0表示真空光速；參數γR、γI分別為：

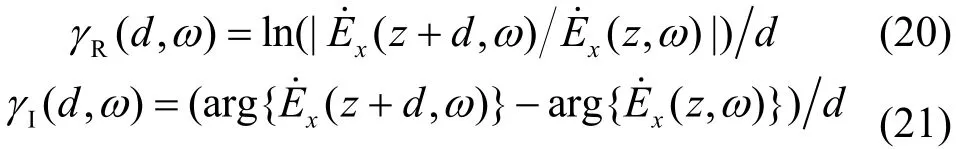
選取d = 20Δz時，復值相對介電常數實部和負虛部的解析值、Padé近似值、FDTD估計值隨頻率的變化關系如圖4所示(頻率軸為對數坐標，后文同)。

從圖4可以看出，在UWB條件下，以一維問題的相對介電常數為測試目標，其FDTD估計值和Padé近似值或解析值之間差異不大(實際結果顯示相對均方誤差均小于1%)；再與文獻[3]中圖4a的結果對比發現，二者也基本保持一致，因此，文獻[3]的單極情形可視為本文改進方案的又一個特例。

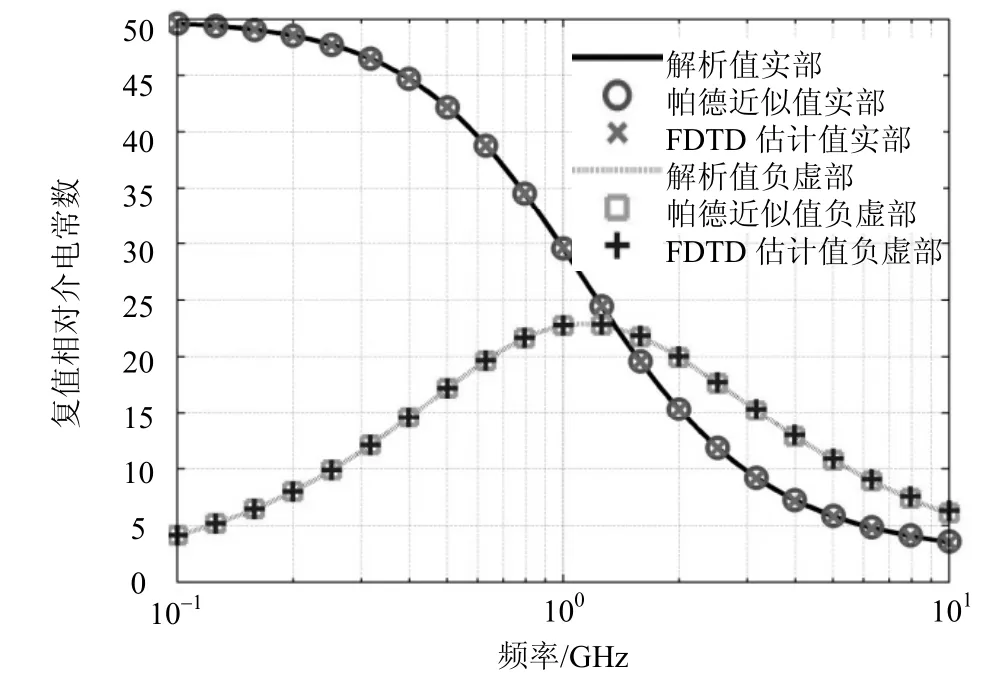
圖4 復值相對介電常數隨頻率的變化關系

算例 4 選取一個更具代表性的三維問題：計算空氣(視為真空)中均勻4極C-C弱磁性介質球的后向雷達散射截面(radar cross section, RCS)[2]，球半徑為50 mm，由浸潤型脂類組織構成，其模型參數(源于實驗測量[17])分別為ε∞= 2.5、σs= 0.035 S/m、Δε1= 9.0、Δε2= 35、Δε3= 3.3×104、Δε4= 1.0×107、τ1= 7.96 ps、τ2= 15.92 ns、τ3= 159.15 μs、τ4= 15.915 ms、β1= 0.80、β2= 0.90、β3= 0.95、β4= 0.99；其余模型參數分別為μr= 1.2、W = 4、α1= α2= α3= α4= 1.0；采用的入射平面波與算例3相同。

FDTD離散化的空間網格尺寸、時間步長分別取為Δ = Δx= Δy= Δz= 3 mm、Δt = Δ/(2.c0)，離散獲得的網格數、時間步數分別為n = 50×50×50、nt= 5 000。主FDTD區域周圍用10層卷積完全匹配層(convolution perfectly matched layer, CPML)[2]吸收邊界截斷。

作為比較，RCS的解析值由Mie級數法[2]獲得，兩種方法的計算結果對比如圖5所示。

通過圖5發現，在較寬泛的頻率范圍，以三維吸波介質球的后向RCS為測試目標，其FDTD估計值和解析值仍然符合較好(結果顯示，相對均方誤差較一維情形有所增加，原因可能是網格剖分粗糙所致，有望通過先進的網格剖分技術進一步減小誤差[2])。

綜合以上4個算例可看出，利用前述FDTD改進方案模擬UWB電磁波在C-C、D-C、H-N等幾類電色散媒質中傳播，估計相對介電常數、后向雷達散射截面所產生的誤差，一般的工程應用可以接受。這些仿真結果初步證實，利用本文發展的FDTD方案，模擬一般電色散媒質中的電波傳播是可行的。

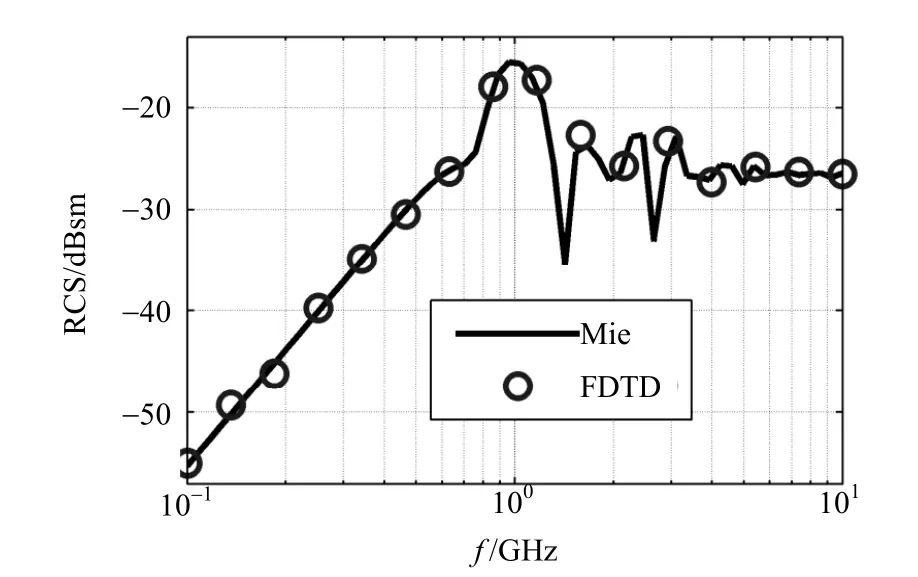
圖5 介質球后向雷達散射截面隨頻率的變化關系

5 結 束 語

本文改進了文獻[7-9]提出的FDTD方案，改進后的方案具有適用范圍廣、實現復雜度低等優勢，適用于統一處理射頻、微波、紅外和毫米波等工程中一般電色散媒質的電波傳播問題，媒質可以是一維或多維的、單極或多極的、無磁或有磁的。算例的初步結果顯示，在超寬帶頻譜范圍，該方案具有較高的數值精度。該方案的魯棒性還需經歷實驗測量、噪聲影響等因素的檢驗。

[1] 陳西良, 陳欣, 朱智勇. 不同極性聚合物材料的THz-TDS光譜測量研究[J]. 紅外與毫米波學報, 2013, 32(2): 150-159. CHEN Xi-liang, CHEN Xin, ZHU Zhi-yong. THz-TDS spectra study of polymer materials with different polarity[J]. Journal of Infrared and Millimeter Waves, 2013, 32(2): 150-159.

[2] 葛德彪, 閆玉波. 電磁波時域有限差分法[M]. 第3版. 西安: 西安電子科技大學出版社, 2011: 259-300. GE De-biao, YAN Yu-bo. Finite-difference time-domainmethod for electromagnetic waves[M]. 3rd ed. Xi’an: Xidian University Press, 2011: 259-300.

[3] REKANOS I T. FDTD schemes for wave propagation in Davidson-Cole dispersive media using auxiliary differential equations[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(3): 1467-1478.

[4] 劉廣東, 張業榮. 一種處理分層有耗色散介質的時域逆散射方法[J]. 電子學報, 2011, 39(12): 2856-2862. LIU Guang-dong, ZHANG Ye-rong. An approach to the time-domain inverse scattering problem for the stratified frequency-dispersive lossy media[J]. Acta Electronica Sinica, 2011, 39(12): 2856-2862.

[5] WANG Ai-hua, CAI Jiu-ju. Modeling of radiative properties of metallic microscale rough surface[J]. Journal of Central South University, 2012, 19: 1482-1487.

[6] 劉廣東, 張開銀, 范士民. 一種處理Cole-Cole色散媒質的FDTD改進方案[J]. 計算物理, 2014, 31(2): 257-265. LIU Guang-dong, ZHANG Kai-yin, FAN Shi-min. A modified FDTD scheme for wave propagation in general Cole-Cole dispersive media[J]. Chinese Journal of Computational Physics, 2014, 31(2): 257-265.

[7] REKANOS I T, PAPADOPOULOS T G. An auxiliary differential equation method for FDTD modeling of wave propagation in Cole-Cole dispersive media[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(11): 3666-3674.

[8] REKANOS I T, PAPADOPOULOS T G. FDTD modeling of wave propagation in Cole-Cole media with multiple relaxation times[J]. IEEE Antennas and Wireless Propagation Letters, 2010(9): 67-69.

[9] REKANOS I T. FDTD modeling of Havriliak-Negami media[J]. IEEE Microwave and Wireless Components Letters, 2012, 22(2): 49-51.

[10] 劉廣東, 張業榮. 二維有耗色散介質的時域逆散射方法[J]. 物理學報, 2010, 59(10): 6969-6979. LIU Guang-dong, ZHANG Ye-rong. Time domain inverse scattering problem for two dimensional frequencydispersive lossy media[J]. Acta Physica Sinica, 2010, 59(10): 6969-6979.

[11] 曹苗苗, 劉文鑫, 王勇, 等. 介質加載復合光柵結構的色散特性研究[J]. 物理學報, 2014, 63(2): 024101. CAO Miao-miao, LIU Wen-xin, WANG Yong, et al. Dispersion characteristics of dielectric loaded metal grating[J]. Acta Physica Sinica, 2014, 63(2): 024101.

[12] 劉瑜, 梁正, 楊梓強. 混合并行技術在FDTD計算中的應用研究[J]. 電子科技大學學報, 2009, 38(2): 222-226. LIU Yu, LIANG Zheng, YANG Zi-qiang. Study and application on hybrid parallel FDTD algorithm[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(2): 222-226.

[13] 王飛, 魏兵. 電各向異性色散介質電磁散射時域有限差分分析的半解析遞推卷積方法[J]. 物理學報, 2013, 62(4): 044101. WANG Fei, WEI Bing. Semi-analytical recursive convolution algorithm in the finite-difference time domain analysis of anisotropic dispersive medium[J]. Acta Physica Sinica, 2013, 62(4): 044101.

[14] 魏兵, 董宇航, 王飛, 等. 基于移位算子時域有限差分的色散薄層節點修正算法[J]. 物理學報, 2010, 59(4): 2443-2450. WEI Bing, DONG Yu-hang, WANG Fei, et al. A modificatory algorithm for electrically thin dispersive layers base on shift operator finite-difference time-domain method[J]. Acta Physica Sinica, 2010, 59(4): 2443-2450.

[15] BAKER G A, GRAVES M P. Padé approximants[M]. New York, USA: Cambridge University Press, 1996: 1-8.

[16] HAVRILIAK S, NEGAMI S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers[J]. Polymer, 1967, 8(4): 161-210.

[17] GABRIEL S, LAU R W, GABRIEL C. The dielectric properties of biological tissues III. Parametric models for the dielectric spectrum of tissues[J]. Physics in Medicine and Biology, 1996, 41: 2271-2293.

編 輯 黃 莘

Improved FDTD Scheme Based on Padé Approximant Method for Modeling of Wave Propagation in General Dispersive Media

LIU Guang-dong

(School of Physical and Electronic Engineering, Fuyang Normal College Fuyang Anhui 236037)

A modified finite-difference time-domain (FDTD) scheme is developed to simulate wave propagation in different electrically dispersive media with isotropic, linear and magnetic properties. The presented scheme is applicable to several types of general frequency-dependent media such as Havriliak-Negami (H-N), Davidson-Cole (D-C), Cole-Cole (C-C), Debye dispersive media or nondispersive media, which are lossless or lossy, with single pole or multiple relaxation times. The main difficulty in this scheme is the appearance of fractional derivatives. Based on the Padé approximant method, a set of auxiliary differential equations (ADEs) of integer order are derived. Thus, this difficulty is circumvented, and its advantage in universality and complexity is also exhibited. The feasibility and validity of the presented scheme are preliminarily demonstrated by the comparisons between analytic and numerical results from several one-dimensional (1-D) and three-dimensional (3-D) examples.

auxiliary differential equation (ADE); finite-difference time-domain (FDTD) method; frequency-dependent media; Padé approximant method

O441.4

A

10.3969/j.issn.1001-0548.2015.06.009

2014 ? 05 ? 30；

2015 ? 06 ? 11

國家自然科學基金(51271059)；安徽省教育廳自然科學研究重點項目(KJ2014A193)；安徽省科技計劃(12010302080, 1501031114)

劉廣東(1972 ? )，男，博士，副教授，主要從事電磁散射和逆散射方面的研究.