旦德林雙球模型定義后的“橢圓的標準方程”的教學

☉江蘇省錫山高級中學 吳寶瑩

·江蘇省無錫市吳寶瑩數學名師工作室·

旦德林雙球模型定義后的“橢圓的標準方程”的教學

☉江蘇省錫山高級中學 吳寶瑩

“橢圓的標準方程”是解析幾何中圓錐曲線的起始課，多次被選為國家、省、市評優課的課題.新教材的設計思路遵循了橢圓發展的歷史：公元前3世紀，阿波羅尼奧斯（Apollonius，約公元前262年～約公元前190年）在《圓錐曲線論》中采用平面截對頂的圓錐得到橢圓，并由多個命題導出橢圓的兩個焦半徑之和等于常數這一性質.17世紀荷蘭數學家舒騰（F.van.Schooten，1615～1660）利用橢圓的兩個焦半徑之和等于常數這一性質，給出橢圓的畫法.直到1822年比利時數學家旦德林（G．P. Dandelin，1794～1847）利用雙球模型總結出橢圓的定義［1］.新教材中第二節課才是橢圓的標準方程，但在實際教學中（包括國家、省、市評優課），由于大部分老師不習慣新教材的設計思路，往往還是沿襲舊教材的做法，把橢圓的標準方程和橢圓的定義安排在一節課上，報刊上發表的有關文章大多也是把二者放在一起.下面就談一談按照新教材的設計思路，旦德林雙球模型定義后的“橢圓的標準方程”的教學的幾點體會，以饗讀者.

一、形成認知沖突，驅動探求欲望

17世紀荷蘭數學家舒騰的橢圓的畫法（基于兩個焦半徑之和等于常數）是在把圓壓扁變成“橢圓”之后總結出來的，教師用幾何畫板再現這一歷史過程，直觀地可以看出圓壓扁后的曲線上任一點到兩個定點F1、F2的距離的和始終等于同一個常數（大于|F1F2|），根據橢圓的定義，圓壓扁后的曲線應當是橢圓，但這只是幾何直觀驗證，有失嚴謹性，需要從代數意義上的嚴格證明，那么又如何證明呢？現有的知識解決不了，這就引起認知沖突，驅動學生進一步探求的欲望，引導學生用代數的方法研究幾何問題，這恰恰是解析幾何的本質特征！聯想類比圓的研究過程，為了研究圓的性質，就要建立圓的方程，而圓的方程實際上就是圓上任一點的坐標（x，y）中x、y的關系，又因為坐標是存在于坐標系中的，所以首先要建立坐標系.于是求曲線方程的一般步驟就自然浮出水面：

然后按照上述步驟推導橢圓的標準方程，直入本節的重點與難點.

二、教學中“突兀點”的處理

數學教學追求合理順暢.數學概念的合理性、數學公式的來龍去脈、為什么要引入某個參數、怎樣引入才不顯“突兀”、怎樣引入才順接學生認知的“最近發展區”等這些問題都值得我們注意.一方面，通過計算機模擬將圓壓扁成橢圓的演示（如圖1，圓心一分為二，兩條重疊的半徑MF分裂成兩條焦半徑MF1、MF2），為學生推導橢圓方程中2a的引入作了認識上的準備，這要比教材中直接設出|MF1|+|MF2|=2a要自然的多，避免了這個“突兀點”.另一方面，如圖2，當點M運動到橢圓的上頂點時，在Rt△MOF2中|MF2|=a，|OF2|=c，所以a2-c2=|OM|2，令b2=a2-c2，這里引入參數b簡化了計算，更重要的是參數b具有確切的幾何意義：線段OM的長（橢圓的中心到上頂點的距離）.這樣的教學就比較合理順暢，不顯得突兀.

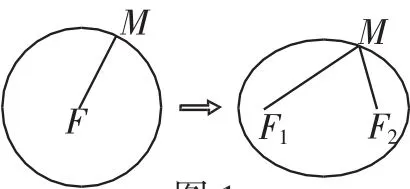
圖1

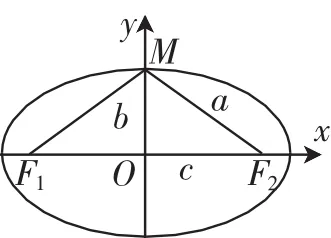
圖2

三、努力提煉數學思想方法

通過引導學生參與探索活動，幫助學生提煉和應用數學知識本身所隱含的數學思想方法.

1.轉化與化歸思想

將|MF1|+|MF2|=2a坐標化為是幾何形式向代數形式的轉化；將化成橢圓的標準方程是化繁為簡的過程，就是轉化與化歸思想的應用.

2.數形結合思想

通過探求橢圓的標準方程，從代數層面上嚴謹證明“圓壓扁變成的曲線是橢圓”是典型的“以數解形”，即幾何問題代數化.

3.分類討論思想

不能確定焦點的位置，不妨就分焦點在x、y軸上兩種情況討論，是很自然的想法，也是很好的方法.

這里用到的就是分類討論的思想，當然教師還可以引導學生分析引起討論的原因，為了避免討論，可設成x2和y2項的分母不分大小的橢圓的方程，即0，n＞0，m≠n），甚至進一步設橢圓的方程為px2+qy2=1（p＞0，q＞0，p≠q），這樣就有一定的靈活性，避免了討論，大大簡化了解題過程，很好地體現了數學的簡潔之美，同時培養了學生精益求精的良好行為習慣.

4.方程的思想

實際上，上述分類討論中用到的待定系數法就是方程思想的應用.另外引導學生在看作兩個未知數，通過解方程（組），解出其中一個，再平方化簡得到橢圓的標準方程，也是方程思想的應用.

數學思想方法是數學知識的精髓，是知識轉化為能力的橋梁，在數學課堂教學中，有意識地提煉和運用數學思想方法，值得每一位數學教師認真關注.

四、注意發展學生的數學理性思維

數學是思維的體操，這里的思維主要指理性思維.一般認為，數學理性思維主要包括三個方面.

（1）從數和形的角度觀察事物，提出有數學特點的問題（存在性、唯一性、不變性、充要性）；

（2）運用歸納抽象、演繹證明、運算求解、空間想象、直覺猜想等思維方式分析和思考問題；

（3）運用數學語言進行表述和交流.

其一，上文中提到的“以數解形”與“以形助數”就是從數和形的角度觀察事物，提出有數學特點的問題的具體體現.

其二，整個標準方程的推導化簡過程，既是歸納抽象，又是演繹推理.尤其在教學時不拘泥于教材中的橢圓標準方程的推導方法，上述有理化的方法，以及把處理，消去參量d后，可得（a2-c2）x2+a2y2=a2（a2-c2）.這些教學處理方法很好地培養了學生思維的靈活性與發散性.

“第一次平方后，從a2-cx=aa2y2=a2（a2-c2）等價嗎？為什么？”“橢圓上的點的坐標都滿足方程嗎？反之，以方程的解（x，y）為坐標的點都在橢圓上嗎？”“a2-cx=a有什么幾何意義？”等這些追問與思考，無不體現了數學理性思維的嚴謹性與深刻性.

其三，圍繞標準方程的推導展開的師生、生生之間的對話，顯然是數學語言的表述和交流.所有這些，都體現了對數學理性思維的要求.

五、努力體現數學的文化價值

數學作為文化的一部分，其最根本的特征是：它表達了一種勇于探索的精神.這種探索精神，將不斷促進人類的思想解放，使人成為更完全、更豐富、更有力量的人.為此，中學數學教學必須充分發掘數學的文化教育功能.

這節課通過引導學生推導標準方程，努力促使教學、學習、研究三者同步協調和諧發展.這一過程對初學橢圓的學生來說有一定的困難，但是經過自己不畏困難的努力與探索欣賞到數學的和諧之美、簡潔之美，可以幫助學生體會追求真理的艱辛以及成功后的愉悅，以此培養學生的探索精神，逐步形成良好的個性品質，而這正是數學文化價值的真諦.

新課程的一個鮮明特點是以學生的發展為本，關注學生思維的最近發展區，注重知識的發生、發展過程的揭示，倡導通過學生參與，自主探究，發現知識，習得知識，重在學生潛能的開發、創新意識和探索發現能力的培養.本節課在這方面作了有益的探索.這節課的教學內容是在學生擁有了圓的方程等知識的基礎上進行研究的，類比圓的方程的建立過程，探求橢圓的標準方程，這是對學生思維最近發展區的有意關注.另外，整節課以“再現定義—親身感知—動手推導—簡單應用”為主線將問題逐一展開.橢圓標準方程的推導由學生自行完成，課堂小結由師生共同完善，這既是對學習主體的充分尊重，使學生獲得親歷知識生長發展的體驗，又是培養學生自我參與意識和探索發現能力、開發學生潛能的有效方式.

誠然，在數學教學中獲得結果，特別是獲得準確的結果是重要的，但從某種意義上說，讓學生經歷和體驗獲取知識的過程要比獲得結果更重要.這是因為這種獲取知識的過程，不僅是知識生長、發展的動態延伸，更是開啟智慧、發展智力、培養潛能、提高素質的源泉.正如一次旅行，不必太在意目的地，重要的是不要錯過沿途的風景！

1.陳鋒，王芳.基于旦德林雙球模型的橢圓定義教學［J］.數學教學，2012（4）.

2.賈士代.推導橢圓標準方程的幾點體會［J］.中學數學，1984（11）.

3.胡挺員.橢圓及其標準方程［J］.中學數學，1999（8）.