平面向量在高中數學中的應用
文/王原光
平面向量在高中數學中的應用
文/王原光
平面向量作為數學工具,是代數和幾何的紐帶,是中學數學知識網絡中的一個交匯點,成為聯系多項內容的媒介。向量和圖象、函數、三角、數列、不等式、平面幾何等基礎知識結合,應用數形結合和化歸與轉化等思想方法,將幾何知識和代數知識有機地結合在一起,能為多角度地展開解題思路提供廣闊的空間。本文從六個方面說明了平面向量在高中數學中的應用。
平面向量;數學思想方法;應用
近年來,我國把坐標和向量、概率分布、導數等陸續納入三年制高中教學大綱,無疑是國家數學課程改革的一個正確方向,也向教育先進國家靠攏邁出了堅實的一步。
坐標與向量,作為現行中學數學教材各成員中的“寵兒”,與其它數學知識有密切的聯系,應用起來非常方便,很討人喜歡。以下根據本人的教學實踐以及組織數學課外興趣小組活動的經歷,與各位同仁談談平面向量如何體現它的工具與紐帶的作用。
一、向量在圖形上的應用
向量源于圖形,它和幾何的關系本是“魚水”關系。許多幾何問題,都可借向量簡單解決。
例1、已知平面上的一個三角形ABC,在已知平面上有一點P,設AP的中點是Q,BQ的中點是R,CR的中點是S.證明只有唯一的一點P使得S=P,另外,設這點為P0時,求△ABC和△P0BC的面積比。
因此,S△ABC:S△P0BC=21k:3 k=7:1.這里,向量加法和定量比分點起了關鍵的定位作用,具有其它方法所沒有的優越性。
用向量法解幾何題,通常分三步進行:
首先,將幾何問題的條件和結論轉化為向量問題,用向量語言表示;然后,設置基本向量,將問題中的相關向量用“基本向量”表示出來;最后,通過“基本向量”進行推理、運算,得出求解結論。其中“基本向量”選取是否恰當,直接影響問題解決的難易程度,這是解題過程中一個關鍵要素。
至于向量在空間圖形上的應用的好處,教材和各種資料已有較多的論述,各類問題都有專門的討論。比如證明共線(面)問題、平行問題、垂直問題、角和距離的求解,以及存在性等問題幾乎都可以用向量來解決,這里就不再舉例了。

二、向量在函數中的運用

三、向量在證明不等式中的應用
設非零向量→a,→b的夾角為θ,則︱→a·→b︱=︱→a︱·︱→b︱·︱Cosθ︱。故→a·→b≤︱→a·→b︱≤︱→a︱·︱→b︱。該不等式結果簡單,但應用廣泛,現舉例如下。
該題證法極多,但構造向量來證明不失為一種好方法。
傳統的不等式的證明要用到分析、綜合的各種“技巧”,而向量法卻回避了這些高“技巧”,較為簡單地解決了這些令人頭痛的問題。
四、向量在三角中的應用
當把向量坐標形式表示,且引進三角函數于坐標中時,向量與三角就交溶為一體了。近年來各省份的高考、模擬考題,經常出現這類問題,應引起足夠重視。



以上用到了向量的數量積定義,坐標表示下的模公式,內積公式以及三角恒等變形,體現了綜合利用三角知識和向量知識解題的能力。這種方法也比傳統的解三角形方法更簡易。
五、向量在數列中的應用
在向量坐標化的情況下,如果考慮的是向量序列,那么向量的問題實際便成了數列的問題。

這類問題的關鍵是利用向量的概念或運算轉化為數列問題,再用數列的有關知識解之。
六、向量在解析幾何中的應用
解析幾何的許多問題,常常用向量語言來敘述。因此,首先要正確運用向量概念把原文“翻譯”過來;以便看出所論問題的實質。
(2)設以原點O為中心,對稱軸在坐標軸上,以F為右焦點的橢圓經過M,且取最小值時,求橢圓的方程。


事實上,向量與解析幾何的結合也是高考命題的趨勢,也應引起重視,從上例可以看出,除了要讀懂“向量語言”外,就是一個運用向量和解析幾何知識綜合解決問題的過程。
最后,要強調的是,向量具有工具性作用,用它可證明許多重要公式。如利用向量的內積,可證明公式Cos(α-β)= CosαCosβ+SinαSinβ


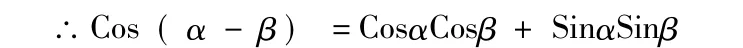

同樣,可利用單位向量和數量積證明解三角形必須的三大定理——射影定理、正弦定理和余弦定理。
綜上所述,向量象一貼強有力的粘合劑,把各部分知識連成一個有機的整體。由于這一點,我們在教學中至少要做以下工作:(1)讓學生掌握向量的基本概念和基本運算,在此基礎上學會運用向量語言;(2)了解向量知識與其它數學知識的交匯作用,應用向量知識盡量簡便地分析和解決問題;(3)經常去對照有關問題的向量解法和傳統解法,把“向量思想”、“向量法”納入基本數學思想或數學方法,并在教學實踐中逐步歸納、總結、完善向量思想,學會舉一反三。這無論對他們應考和將來的深造,都是有益的。
(作者單位:長汀一中)
[1][日]圣文社編《大學入學考試·數學試題選》人民教育出版社。1979,12
[2][日]矢野健太郎著《數學解題技巧》(第二卷上冊)黑龍江人民出版社。1983,10
[3]《新概念教材·奧賽全解》(高一數學)南方出版社2005,5
[4]《2005全國各省市高考模擬試題匯編·數學》西藏人民出版社2005,7
王原光,男,中學一級教師,研究方向:高中數學教學。

