基于切比雪夫最佳逼近意義下的CPI指數變化通道的原理與方法＊

顧樂民

（同濟大學 材料科學與工程學院，上海 200092）

1 引 言

居民消費價格指數（Consumer Price Index，簡稱CPI指數），是普通消費者所購買的物品與勞務的總費用的衡量標準，反映了一定時期內價格變動程度和趨勢的相對數．CPI指數不僅受商品價格的影響，比如糧價［1］、房價［2］等，也有對其權重經常進行調整的一個動態過程，這使得CPI指數變化具有隨機性大、難以找到一般變化規律、難以進行預測等特征．對CPI預測理論及方法成為許多學者關注的問題，目前主要有，基于小波分解自回歸模型分析法［3］、VAR 模型法［4］、ARIMA 模型法［5］、神經網絡法［6］、灰色 GM（1，1）模型法［7］等．

2000年以來的CPI指數積累了186組數據，數據是離散的，孤立的，數據之間的關系是不明確的，數據的來源是有一定統計誤差的．這些看似雜亂無章的數據背后，仿佛總有一只無形的手在操縱著CPI數據的變化，稱這只無形的手為“隱函數”．或許這只無形的手根本就不存在，因為CPI指數的波動含有大量的“人類因素”，或許存在但目前難以找到，但這不影響探討的本質．任何一個運動、變化、發展的事物，都存在其本質的內在規律，都是可以從變化的過程中找到．

構建隱函數的目的，是要用數學的方法來探索CPI變化的某些規律．CPI指數屬于一種“近程有序，遠程無序”的數據變化形式，在較短的局部范圍內，其變化具有一定的規律可循．從長期全局范圍看，其變化呈大波動狀失去規律．這也就是說，用具有軌跡特征的曲線是難以描述這種變化的，必須用其它的方法，一種既包含著曲線又不局限于曲線的方法去描述．

切比雪夫（P．L．Chebyshev，1821～1894）創立的最佳一致逼近原理，最早源于19世紀對機器的機械運動按理想設計運動的研究．將該原理運用于CPI指數變化，可以構建一條切比雪夫最佳逼近意義下的CPI指數變化通道．CPI指數變化是有限的變化，可以用2條曲線，1條稱為上界限，另1條稱為下界限，將所有的數據都囊括其中，并形成一條延伸的通道．通道將雜亂無章的數據加以規范和約束，而隱函數必定在通道之內，通過數學的方法可以找到最佳逼近意義下的隱函數，使CPI的變化成為可知與可控．由于通道具有連續性，變化具有慣性，所以通道的外延具有一定的預測效應，可以推斷出未來可能的變化趨勢，為決策提供有價值的參考．

切比雪夫最佳逼近意義下的數據通道的建立與應用，文獻［8］有較為詳細的描述．由于CPI指數具有變化莫測的特殊性，從最簡單的“直線通道”入手，通過建立通道而闡述其基本的原理與方法，并用186組數據按序做30個數據處理的實例，以檢驗預測的效果．

2 原理與方法

切比雪夫最佳逼近的核心是最大絕對值誤差極小化，由此構成了極小極大曲線擬合法，適用于一個封閉系統內的描述，具有廣泛的應用［9］．由于最大誤差一般都是在端點處出現，在定義區間外是發散的，這從切比雪夫多項式的所有圖形中可以看出，所以不適合用于預測．對預測而言，預測的誤差越小越好，而不是最大甚至發散．零誤差型極小極大逼近是切比雪夫最佳逼近原理的一個推廣，是通過若干零誤差點限制端點誤差為最大，達到端點外誤差不發散的目的，其理論基礎是零誤差型切比雪夫多項式［10］，以及相應的預測理論［11］．對于 CPI指數的預測，只需提供1個零誤差點，在坐標系上是指最右端（簡稱端點，下同）的數據點，這使復雜的問題可以簡化敘述．

2．1 零誤差型極小極大法（Z－Minimax method）

數據 （xi，yi）i＝1，2，…，m是隱函數y（x）在有定義的區間內給出的m個離散點組，為找到隱函數y（x），設擬合函數f（x）＝f（x，a），其中參數a＝（a1，a2，…，an），n≤m，而a1，a2，…，an為n個不全為零的實數．為使f（x）盡可能接近y（x），設誤差函數r（x）＝y（x）－f（x），而誤差值ri是誤差函數r（x）上的具體數值：

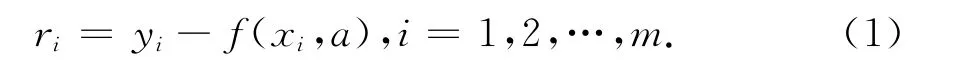
零誤差型極小極大法，是將端點數據誤差設定為零誤差rm＝0條件下，依據最大絕對值誤差極小化的準則來選擇參數a，即依據而構成的一種方法，是切比雪夫最大絕對值誤差極小化基本準則的一個推廣．

2．2 解的實現

如果零誤差型極小極大解存在，即存在a＝a＊使

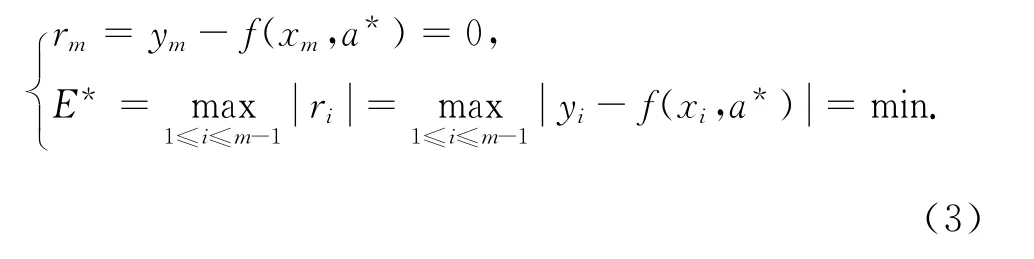
則至少存在1個零誤差點和n個切比雪夫交錯點x1，x2，…，xn使

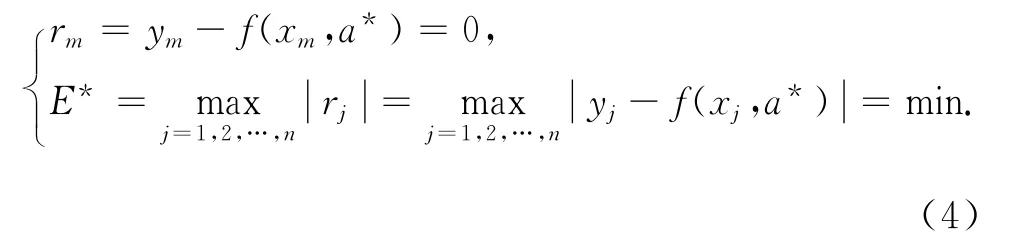
稱參數a＊為極小極大最佳擬合參數，稱f（xj，a＊）為極小極大最佳擬合方程，稱E＊為最佳逼近值，它們構成了零誤差型極小極大逼近的一般解．

2．3 零誤差

所謂零誤差就是沒有誤差或誤差為零．當將端點數據的誤差設定為零時，可使短期的預測得到保證．從曲線變化的一般規律來看，零誤差的兩端是以“－，0，＋”或“＋，0，－”形式出現，越接近零點，誤差絕對值就越小．這就給出一個提示，將端點誤差設定為零誤差即ym－f（xm）＝0，則對于端點外臨近的數據，其預測誤差rm＋1＝ym＋1－f（xm＋1）的絕對值也必定不會大，這為預測的準確性提供了理論依據，僅在出現大隨機誤差的特例下才會無法成立［11］．

2．4 CPI通道

某個變化的過程和狀態可用“通道”來描述，例如，處于下降（或上升）的通道之中等．通道，來往暢通的道路，與交通圖中的道路相似，是擬人化的表達．零誤差型極小極大逼近意義下的CPI指數變化通道，簡稱CPI通道（下同）有以下幾個特征：

1）通道的構成．通道由1條中心線，2條邊界線共同構建；中心線是CPI函數轉化的曲線，也稱為路線是前行的指導線；邊界線是距中心線兩旁±E的曲線．通道用Channel（x）表示：

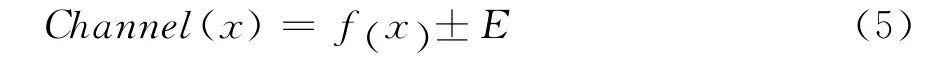
2）通道的作用．通道將離散的、有隨機誤差的數據加以分類和規范，它依據最佳逼近值±E將全部的數據規范在通道內，指出了位于邊界線上的數據，由于偏離中心線最遠，屬于波動最大的大誤差數據；通道將端點數據的誤差設定為零誤差，廢除了所有數據是權重相等的慣例，使權重往端點數據傾斜，并使對未來的預測建立在零誤差的基礎上；通道包含了所有的數據，所以隱函數必定在通道內，通過數學方法可以找到最佳逼近意義下的隱函數，或近似隱函數．

3）通道的意義．將理論的指導路線與實際行走的軌跡聯系在一起，數據沿著中心線前行，但實際是在偏離和糾正偏離中前行的；通道指出了數據變化的最大范圍，限定了安全的最大界線；在最大安全范圍內去探尋隱函數，從而找到CPI變化的某些規律，用于解釋過于、指導現在、預測未來．

3 具體算法

由于CPI數據的隨機性，波動性，難預測性，用通道的原理和方法尋找數據之間的關系有較好的效果．下面用圖示法加以介紹，用的是直線型通道．圖1橫坐標x是月，縱坐標y是CPI指數值（無量綱）．圖中參與計算的CPI數據yi是12個，均在虛線之內，虛線外的數據有1個，不參與計算．

3．1 通道的構成

通道的中心線是擬合函數描述f（x）＝f（x，a），與2條邊界線共同構建成通道f（x）±E．通道內包含了12個數據．由式（4）產生的最大正負誤差點位于邊界線上，如圖1中的點A和點B．通道內有1個零誤差點，位于數據的端點，如圖1中的點C．

3．2 零誤差點

零誤差點是人為設置的點，目的有3個：首先是將相等權重的數據變為不等權重，一般而言，距離現在最近的數據應該有較大的權重，而較遠的權重可以較小，這對于預測而言是合理的，所以端點數據是權重最大的數據．其次是使未來的預測建立在誤差為零的基礎上，這對于未來的預測誤差，難以判斷是正還是負而言，是合理的．再次是一般在零點附近的數據其誤差絕對值一般都是較小的，這使短期預測準確性有了理論上的依據．

3．3 邊界線

大誤差數據的出現，會使邊界線外移，使通道變寬．為使通道收窄，必須將最大（正負）誤差極小化．圖中由點A和點B的這2個最大誤差又都是極小化的，所以邊界線也是極小化的，使通道收窄．從安全意義上說，切比雪夫最佳逼近意義下的通道，是最窄的通道，也是數據變化的最大安全范圍，超出這個范圍就有可能是不安全或欠安全的．

3．4 預測假設條件

若未來短期CPI指數的變化不存在突變，或存在突變但其最大絕對誤差不大于通道內的最大絕對值誤差，則通道的外推延伸能較好的給出未來CPI指數變化的趨勢．預測是建立在預測值f（xm＋1）與最大正負誤差±E基礎上的，描述了CPI指數未來可能的數值與最大的波動范圍：f（xm＋1）±E．從統計概率角度出發，大部分變化不會超出f（xm＋1）±E，這樣就使得CPI指數未來的變化成為可知與可控．

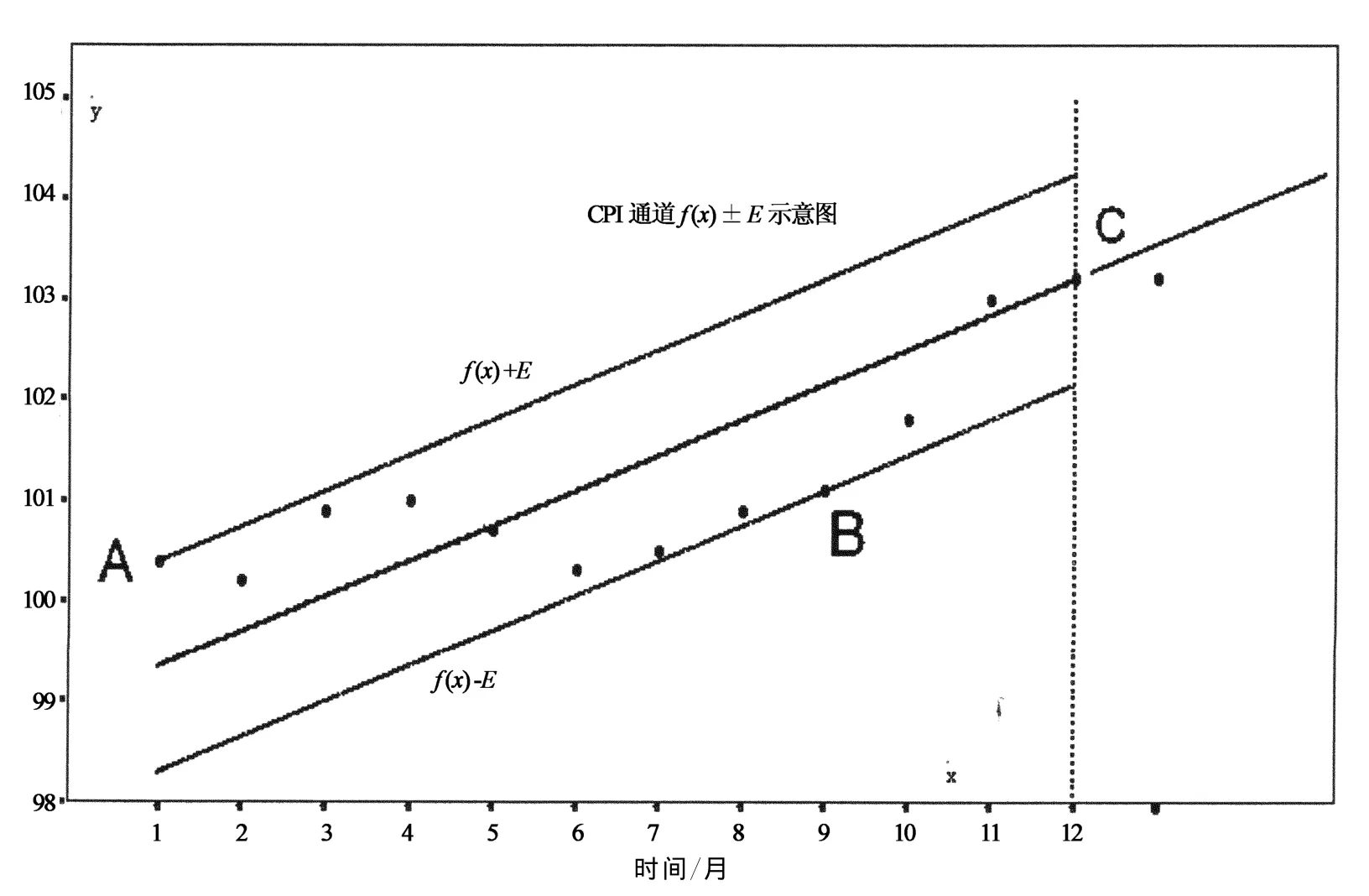
圖1 CPI指數變化通道示意圖

3．5 判斷法則與具體算法

判斷法則主要是判斷異常解是否存在，以及如何處理的問題．

最大絕對值誤差與最小絕對值誤差（即零誤差）之間在本質上是不相容的，強制將原本是最大誤差的端點改為零誤差點，會導致方程結構大的改變，甚至會使方程出現一種病態狀，結果是預測準確性變差．異常解出現的原因一般在于數據的隨機性偏大，數學模型選擇的不當所致．具體算法包含判斷法則，主要步驟如下．

1）判斷：先用最小二乘法對數據進行預處理，進行判斷．若用最小二乘法的數據處理，其最大絕對值誤差出現在端點，且該誤差值較其他誤差值明顯放大，則該點就是異常數據點，其解將可能會出現異常．最小二乘法是個簡單方便的數據處理法，它所獲得的最大絕對值誤差一般也是極小極大法的最大絕對值誤差，所以用最小二乘法進行預處理，用的是其方便與有效．

2）處理：對于異常數據，可以通過增加或減少數據數目，或轉移零誤差點，或改變數學模型等方式進行處理；若異常數據雖然存在，但誤差在允許的范圍內，可不作處理．

3）求解：取直線方程為f（xi）＝a＋bxi，對于式（4）設1≤j，k≤m－1，j≠k，可以通過

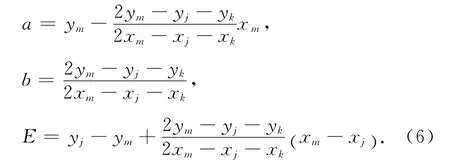
獲得參數a，b及逼近值E．取不同的j，k，使最大的E為極小minmaxE＝E＊，從而獲得最佳逼近值E＊，此時獲得的參數即為最佳參數a＊，b＊．

4 數值分析

2000年1月－2015年6月我國CPI指數來自國家統計局，共186個，每年的數據是12個，歸為1組（2015年除外），共有15組數據，先以2003年的數據處理為例．

4．1 實例一

2003年1月到12月的CPI數據有12個，由判斷法則進行預處理，用最小二乘法得到的方程用P2003（xi）表示：P2003（xi）＝99．41＋0．26xi，經判斷，端點i＝12不是最大誤差點，可以運用零誤差型極小極大逼近，得到的方程用f2003（xi）表示，其中xi＝1，2，…，12：

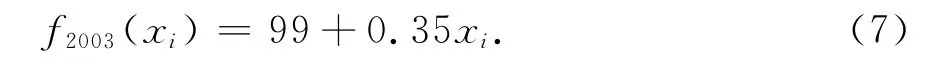
極小化的最大絕對值誤差出現在i＝1，9處，為max｜r｜＝1．05，由此構建的2003年CPI通道為：

Channel2003（x）＝f2003（）x±1．05，其中f2003（）x是f2003（xi）在去掉下標“i”后的函數表達，定義區間為［1，12］．將x13＝13代入，得2004年1月CPI指數預測值及波動值：103．55±1．05．已知2014年1月CPI指數是103．2，在預測的范圍之內．將預測值與實際值進行比較，預測的誤差為0．34%．

文中的圖1就是2003年1月至12月的CPI變化，以及CPI通道，在虛線外的點就是2014年1月的CPI指數，圖中有關說明可參見前文．

4．2 實例二

如法炮制，按序將2000，2001，…，2014年1月至12月的數據處理結果列于表1．

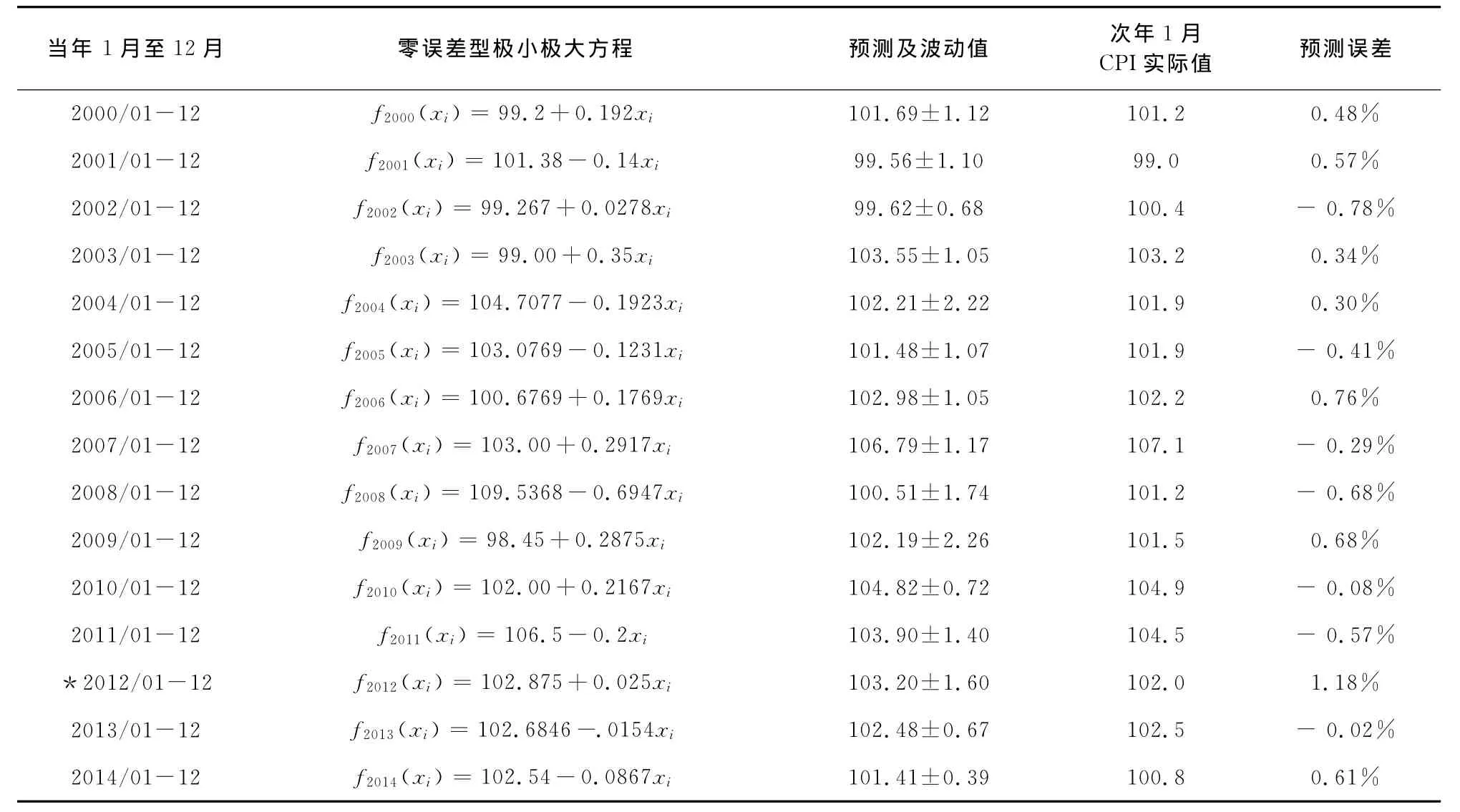
表1 我國2000～2014年，每年1月至12月CPI指數的數據處理及預測

從表1結果看，CPI實際值都落在預測值及波動范圍之內，所以預測的結果是有效的．其中2012年帶＊的數據屬于異常的數據處理，該年11月的CPI指數為102．0，但12月增至104．6，而次年1月又回落到102．0，計算表明12月份的數據屬于異常數據，通過零誤差點遷移，取絕對值誤差最小的點為零誤差點，獲得表中的方程式．

4．3 實例三

表2是按序2000，2001，…，2014年，當年6月至次年5月的12個CPI數據處理以及對次年6月預測情況，共15組．其中帶＊的2013／06－2014／05因出現3個零誤差點，故斜率為0，屬于特殊方程．為了與表1區別，方程用符號g（xi）表示．

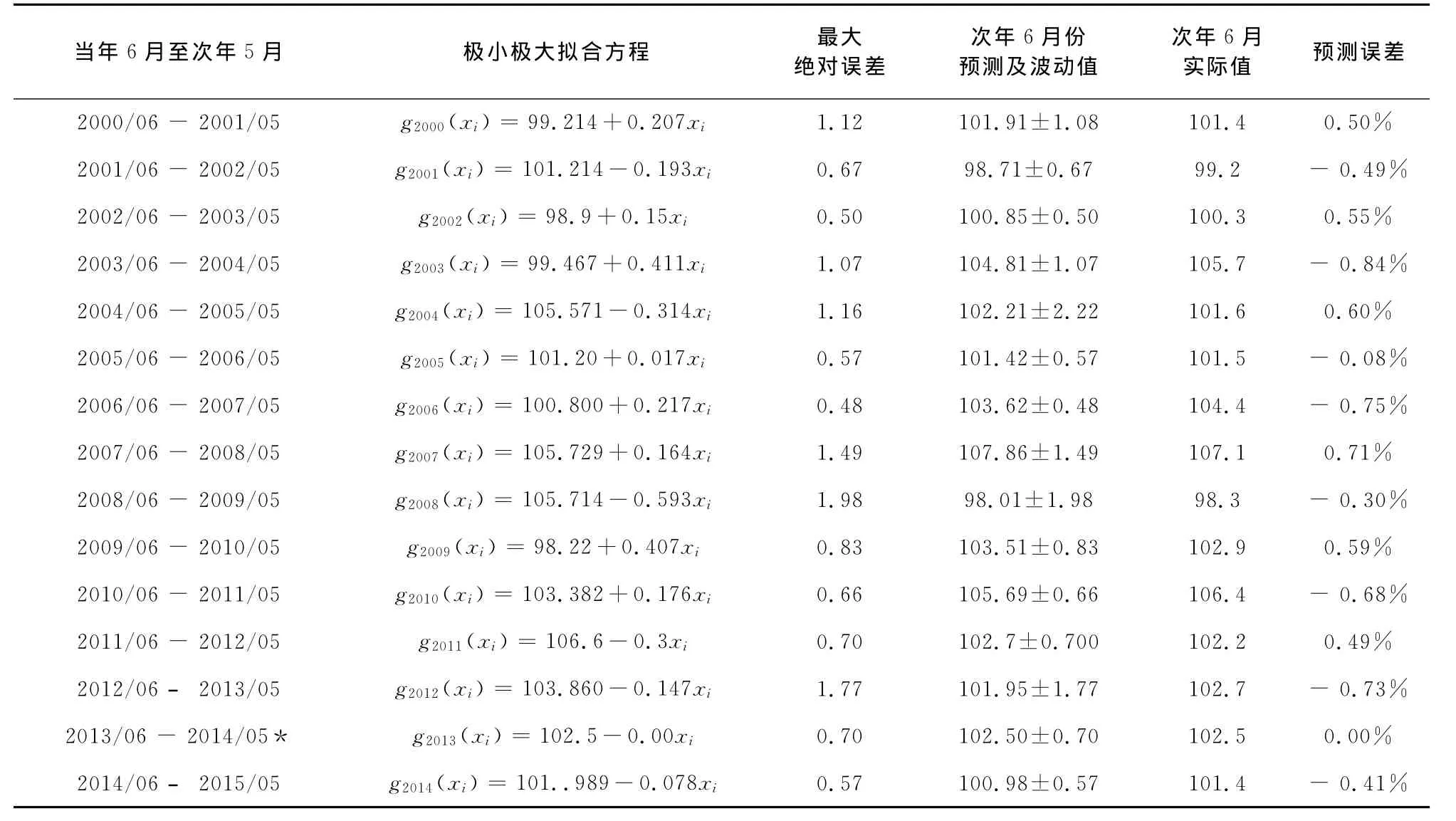
表2 我國2000～2014年，當年6月至次年5月CPI指數的數據處理及預測

5 結 論

提供的通道原理與方法，具有簡單易懂、直觀性強、計算方便、適用范圍廣、符合性較好等特點，是曲線擬合的一種推廣，目的是使預測及預測誤差成為可知與可控．由于直線通道是一個簡單的通道，在進一步的探討中還需要逐步加以完善．

［1］鄒正方，黎智，李迪．國際糧價波動對我國CPI影響的實證分析：以玉米、大豆為例［J］．數學的實踐與認識，2012，42（17）：41－46．

［2］黃飛雪，金建東．金融危機前后中國房價指數對CPI的影響［J］．經濟數學，2010，27（3）：64－72．

［3］陳升，李星野．基于小波分解自回歸模型的CPI預測［J］．統計與決策，2012，349（1）：18－20．

［4］李慶華．基于VAR模型的中國消費價格指數分析［J］．華中師范大學學報（人文社會科學版）．2006，45（4）：56－61．

［5］張本麗等．基于ARIMA模型的山東省居民消費價格指數分析［J］．魯東大學學報，2010，26（3）：285－288．

［6］劉海萍．神經網絡在CPI預測中的應用［C］．第五屆（2010）中國管理學年會——市場營銷分會場論文集，2010．

［7］曾波．居民消費價格指數的 GM（1，1）模型預測［J］．統計與決策，2009，289（13）：7－8．

［8］顧樂民．基于切比雪夫最佳逼近原理的俄羅斯人口變化通道［J］．俄羅斯研究，2015，191（2）：178－192．

［9］Gu LEMIN．Minimax curve fitting method in application of CD production function—— with the grain yield data in China as the example［J］．Journal of Modern Agriculture．2013，2（3）：43－55．

［10］Lemin GU．Zero－Error Type of chebyshev polynomials［J］．International Journal of Modeling and Optimization．2013（3）：272－277．

［11］顧樂民．預測型切比雪夫多項式［J］．計算機工程與應用．2012，48（7）：34－38．