無窮積分的幾個定理
蔡 瑾
(蘇州健雄職業技術學院 軟件與服務外包學院,江蘇 太倉 215411)
無窮積分的幾個定理
蔡 瑾
(蘇州健雄職業技術學院 軟件與服務外包學院,江蘇 太倉 215411)
文章給出了關于無窮積分的三個定理及其證明,證明了收斂(或發散)的正值函數的無窮積分沒有一個收斂(或發散)最慢的,且給出了構造收斂或發散更慢的無窮積分的一種方法.
無窮積分;收斂;發散
1 問題的提出
根據判別無窮積分的幾種方法[1]188-204,本文討論了關于正值函數f(x)使之無窮積分收斂與發散更慢的方法.


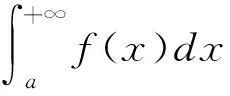
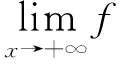
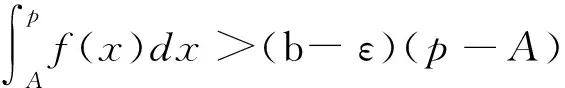
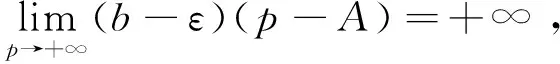
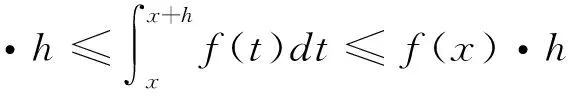

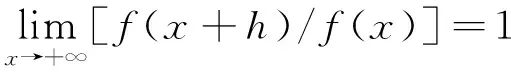
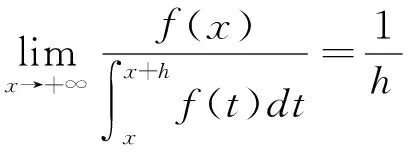
2 定理及證明
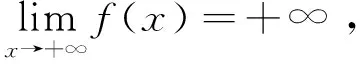
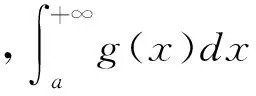

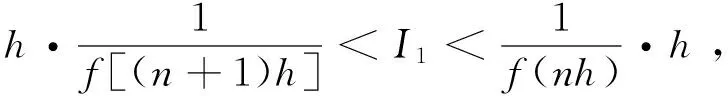

p>1時,x充分大時,f(x)≥1,所以fp(x)≥f(x)
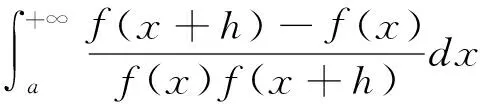
0 又因? p<0,x充分大時,有f(x)≥1,fp(x)≤1, 經驗定性法是根據區域的地貌特征、氣候差異特點、水資源分布狀況等客觀存在的區域表現,主要考慮的是自然因素,常用來進行高級分區。本研究在用該方法時,主要考慮上述干旱分區指標體系中的地貌、降雨量和受災率等3個自然因素,同時兼顧流域內干旱指數的因素,由于海拔較高的山區和丘陵區蓄水能力較弱,降雨量可能不能準確地反映當地的干旱程度,因此在這些地區以受災率指標為主,降雨量指標為輔,而在海拔較低的丘陵和平原地區則以降雨量因素為主,受災率指標為輔助指標,最后完成區域的一級干旱分區。 從而x充分大時,有 證明 令 (x)→C.(x→+∞) 令 由引理3知: 2)如果f(x)是單調遞減趨于0,令F(x) 由引理3知: 通過本文的論證,能夠得出一個很好事實,收斂的正值函數的無窮積分沒有一個收斂得最慢的,在發散的正值函數的無窮積分中沒有一個發散得最慢,并且給出了構造的方法.進一步證明了在比較法中,不存在普遍適用的函數. [1] 劉玉鏈,傅沛仁. 數學分析講義[M].北京:高等教育出版社,1992. [2] 鄒承祖. 數學分析習題課講義[M].長春:吉林大學出版社,1986. [責任編輯 迎客松] 2015-07-12 江蘇省現代教育技術研究2013 年度重點課題(項目編號:2013-R-25012) 蔡 瑾(1967- ) ,女,江蘇太倉人,蘇州健雄職業技術學院講師,主要從事高等數學教學與研究工作。 1671-8127(2015)05-0001-03 O172.2 A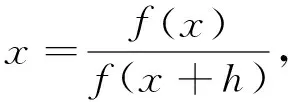
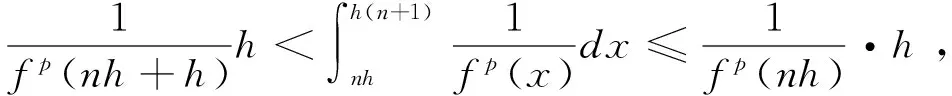
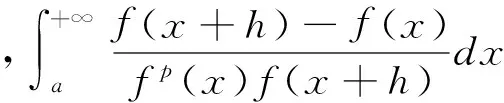
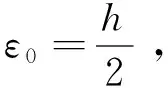
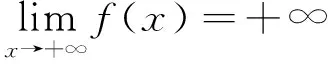
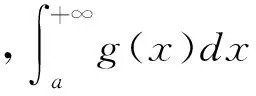
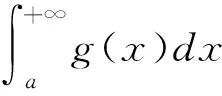
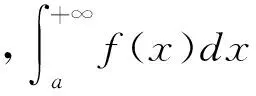
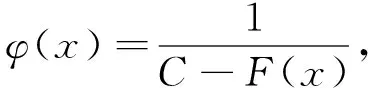
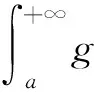
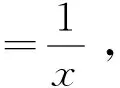
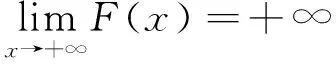
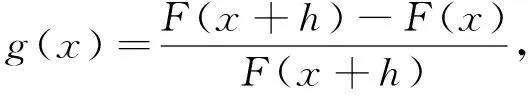
3 結語

