機床支撐地腳結合部法向粗糙接觸建模

田紅亮，余 媛，張 屹

（三峽大學 機械與動力學院，湖北 宜昌443002）

將式（39）代入式（42）得［12］

機床整機動態特性是指機床整機結構在動態力作用下所展現出來的動態特性，通常包含振型、固有頻率、阻尼比、諧響應、動剛度、動柔度等［1］.國內早在從20世紀80年代初期開始，北京機床研究所與陜西機械學院開展對整機動態特性的研發，編制了“金屬切削機床樣機試驗規范總則（試行稿）”，并開發了機床整機結構參數優化分析軟件包［2］.Greenwood等［3］率先研究了粗糙表面的微觀接觸機理，架構了粗糙表面的彈性接觸理論，即GW 理論.Polycarpou等［4］對GW 理論中簡單的指數分布進行了修正，采用修正的指數分布推導出了接觸粗糙表面法向接觸參數的解析近似解.Chang等［5］考慮微接觸點的2種變形方式，純彈性和塑性，根據兩半球體微接觸點在塑性變形時球臺體積守恒建立接觸粗糙表面實際接觸面積和法向接觸負載的分析解，但該模型只考慮了微凸體的完全彈性變形與完全塑性變形機制，沒計及兩者之間的彈塑性過渡變形機制，因此在臨界屈服點處導致法向接觸載荷不連續.Tian等［6-9］聯合分形理論和等效虛擬材料的有限元建模思路分析了螺栓結合部的接觸特性.尤晉閩等［10］基于對粗糙表面形貌統計分析的基礎上，綜合考慮微凸體的完全彈性、彈塑性與完全塑性3種變形機制，構建了結合部的接觸面積、接觸載荷與接觸剛度的統計模型.Zhao等［11］按照微凸體變形的連續性以及光滑性，用模板3次多項式擬合了彈塑性變形階段，提出了一種結合部彈塑性接觸模型，但對于彈塑性變形區間接觸壓應力的估計不夠準確.機床的安裝通常需要在床身與地基之間放置可以調整機床水平的支撐地腳，但現有文獻在對機床整機動態特性進行分析時，大多忽略了地腳的影響.近年來隨著機床向高速化發展，在高速切削領域機床的動態特性對機床性能的影響更加顯著.隨著有限元理論、分析軟件、機床振動測量與分析儀器的發展，當前國內外又一次開展了機床動態特性研究熱潮.

綜上所述，現有的微觀接觸力學理論還未對地腳進行全面的研究，本文在以上研究的基礎上，以混凝土地坪與標準平板互相接觸形成的金屬切削機床底座支撐地腳結合部為考察對象，考慮微接觸點的2個彈塑性變形區域，構架干摩擦金屬結合部法向接觸參數的統計模型.

1 地腳結合部的微觀變形與宏觀參數

機床底座支撐地腳結合部的組成見圖1.

混凝土地坪與標準平板的微觀接觸見圖2，其中，z為混凝土地坪微接觸點的高度，d 為混凝土地坪與標準平板之間的間距，w 為微接觸點的法向變形量，R 為微接觸點的半徑.

微接觸點的法向變形量為

微接觸點的彈性臨界法向變形量［5］為

式中：K 為最大接觸壓應力因子，K ＝0.454＋0.41ν，ν為較軟材料的泊松比；H 為較軟材料的硬度；E 為當量彈性模量，表達式為

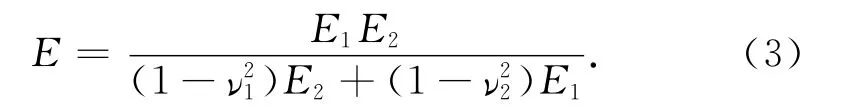
式中：E1與ν1分別為混凝土地坪的彈性模量與泊松比；E2及ν2依次為標準平板的彈性模量及泊松比.

Kogut等［12］認為，當wc≤w ≤110wc，微接觸點處于彈塑性變形范圍.根據數值計算結果，整個彈塑性階段又分為彈塑性變形Ⅰ區（wc≤w ≤6wc）和彈塑性變形Ⅱ區（6wc≤w ≤110wc）.

1.1 微接觸點的彈性變形

當w ＜wc時，微接觸點發生彈性變形.單個微接觸點的彈性接觸面積為

整個結合部的實際彈性接觸面積為

式中：η為微接觸點的面密度；An為名義接觸面積；φ（z）為微接觸點高度分布的概率密度.

將式（4）代入式（5）得

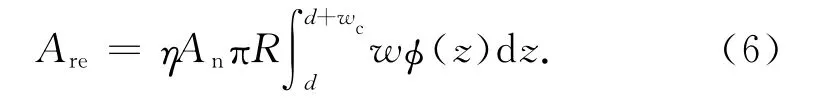
將式（1）代入式（6）得

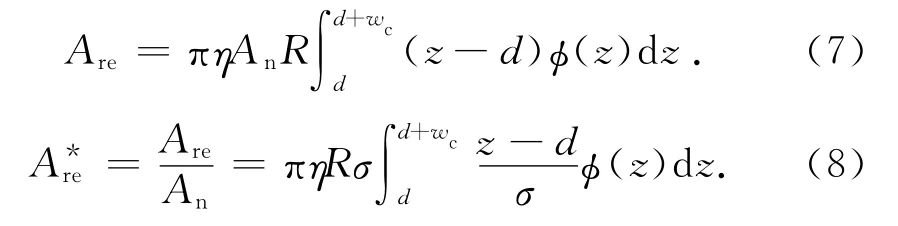
式中：σ為微接觸點高度分布的標準差.

式（8）可變為［13］

式中：β ＝ηRσ 為表面粗糙度參量；z＊＝z／σ；d＊＝d／σ；w＊c＝wc／σ；φ＊（z＊）＝σφ（σz＊）；φ（z）dz＝φ＊（z＊）dz＊.

單個微接觸點的彈性接觸負載為

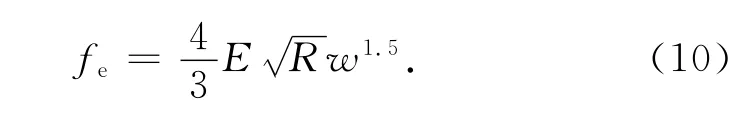
整個結合部的彈性接觸負載為

將式（1）代入式（12）得

將式（17）代入式（15）得［13］

由式（10）可得微接觸點與標準平板的彈性接觸剛度為

若w ＜wc時，由彈性接觸剛度引起的彈性應變能為

整個結合部的彈性接觸剛度為

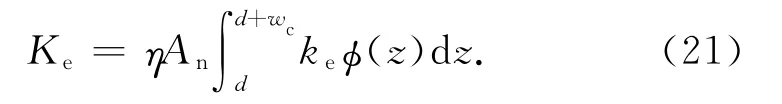
將式（19）代入式（21）得

將式（1）代入式（22）得

1.2 微接觸點的彈塑性變形

當w ＝wc時彈性臨界接觸 面積ac滿足［12］

第Ⅰ彈塑性接觸面積aep1滿足［12］

整個結合部的第Ⅰ實際彈塑性接觸面積為

將式（1）代入式（31）得

量綱為1的第Ⅰ實際彈塑性接觸面積為

式（33）可變為［13］

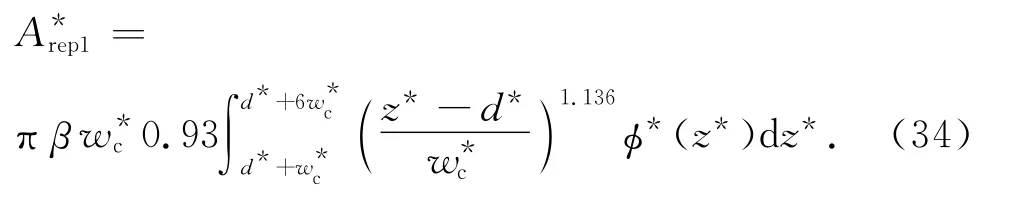
當w ＝wc時，彈性臨界接觸負載fc滿足［12］

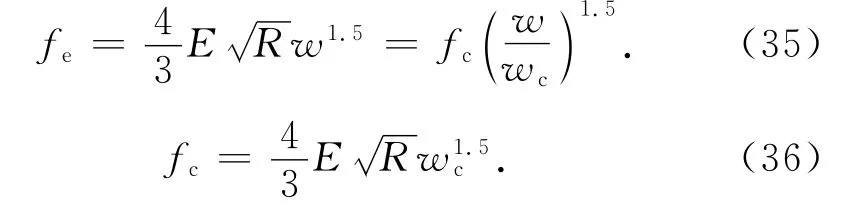
當w ＝wc時，平均接觸壓應力為

將式（27）和（36）代入式（37）得

將式（2）代入式（38）得［12］

平均彈性接觸壓應力［12］為

將式（26）和（35）代入式（40）得

將式（37）代入式（41）得［12］

將式（39）代入式（42）得［12］

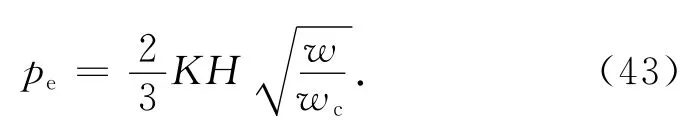
將式（43）代入式（41）得

將式（27）代入式（44）得

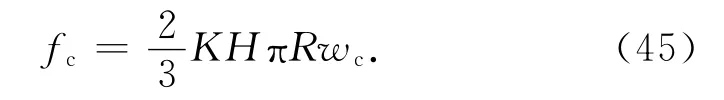
第Ⅰ彈塑性接觸負載fep1滿足［12］

整個結合部的第Ⅰ彈塑性接觸負載為

將式（1）代入式（49）得

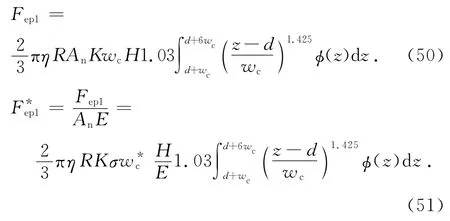
式（51）可變為［13］

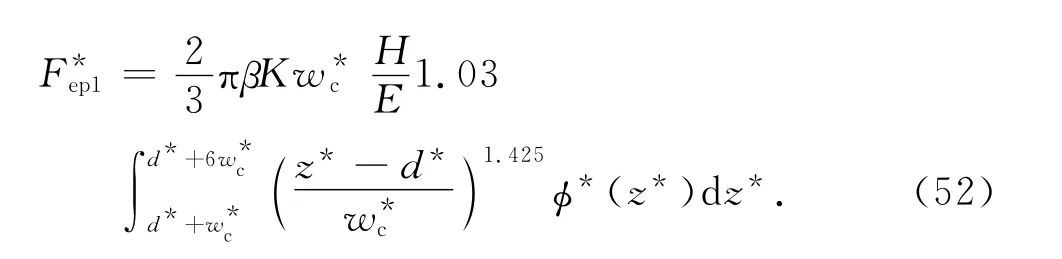
發生彈塑性的微接觸點產生彈塑性應變能.沒有達到彈性極限的微接觸點對彈性應變能有貢獻，根據式（20）可得區域Ⅰ的彈性應變能為

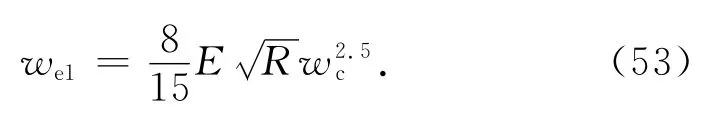
按照式（19），彈性接觸剛度隨著w 的增加而增加，直到w ＝wc時達到最大值為止，因此第Ⅰ彈塑性接觸剛度為

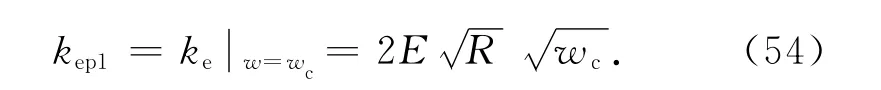
整個結合部的第Ⅰ彈塑性接觸剛度為

量綱為1的第Ⅰ彈塑性接觸剛度為

式（57）可變為

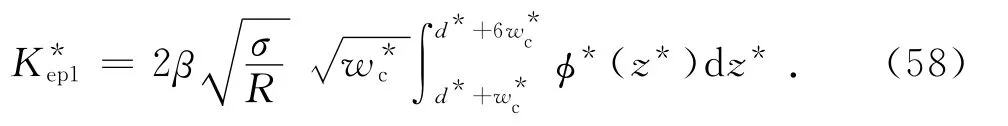
第Ⅱ彈塑性接觸面積aep2滿足［12］

將式（27）代入式（59）得

整個結合部的第Ⅱ實際彈塑性接觸面積為

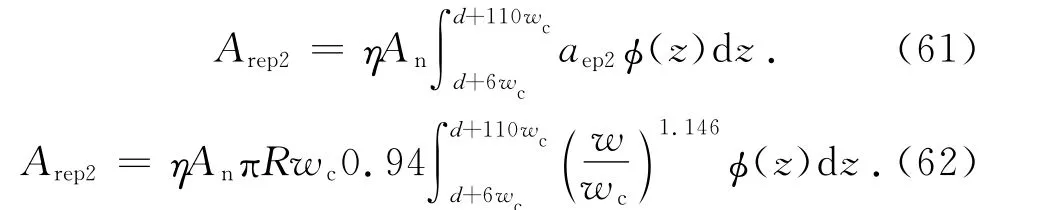
將式（1）代入式（62）得

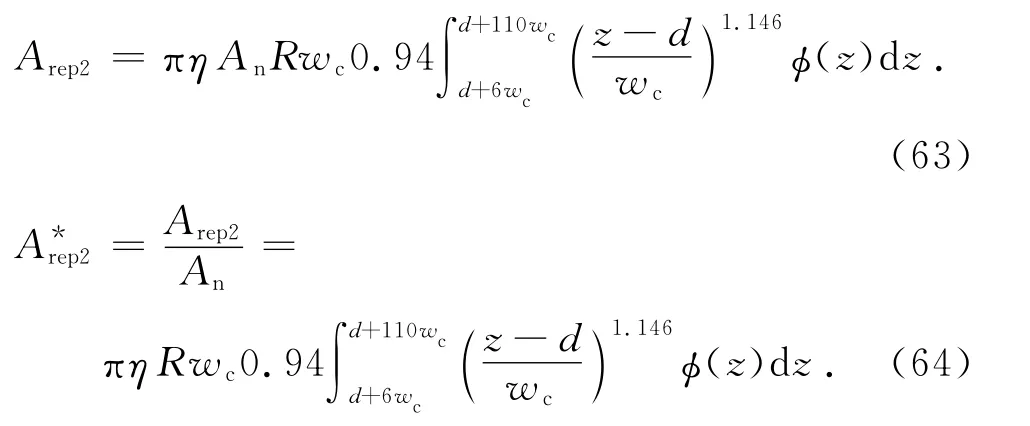
式（64）可變為［13］

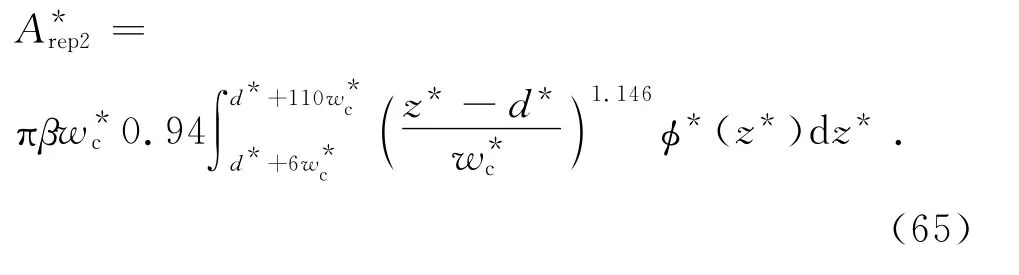
第Ⅱ彈塑性接觸負載fep2滿足［12］

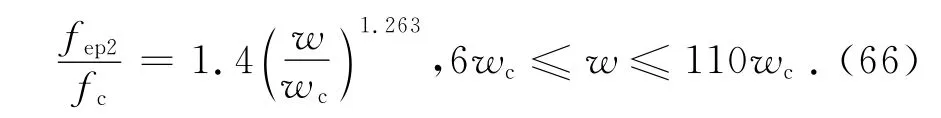
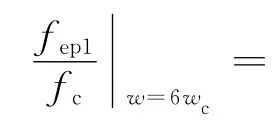
將式（45）代入式（66）得

整個結合部的第Ⅱ彈塑性接觸負載為

將式（1）代入式（69）得

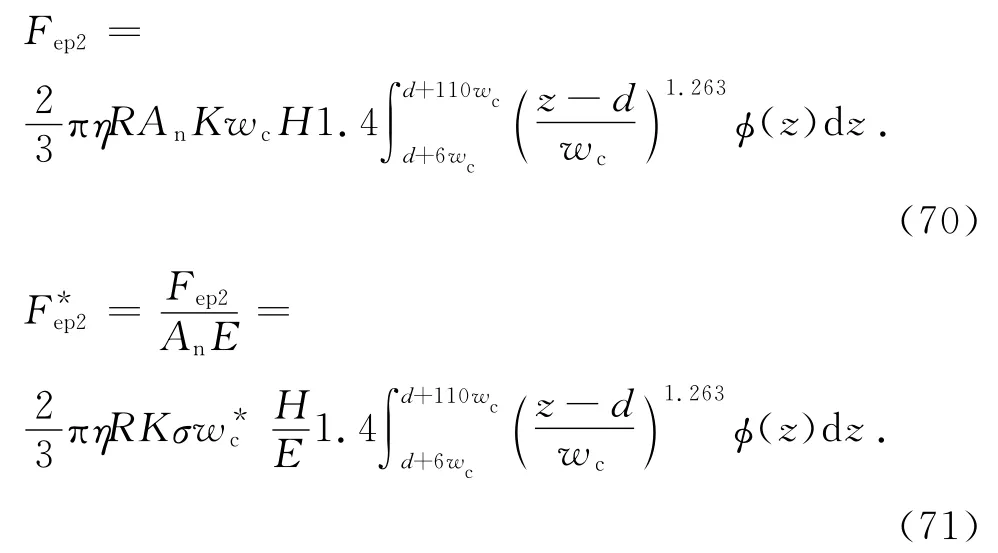
式（71）可變為［13］

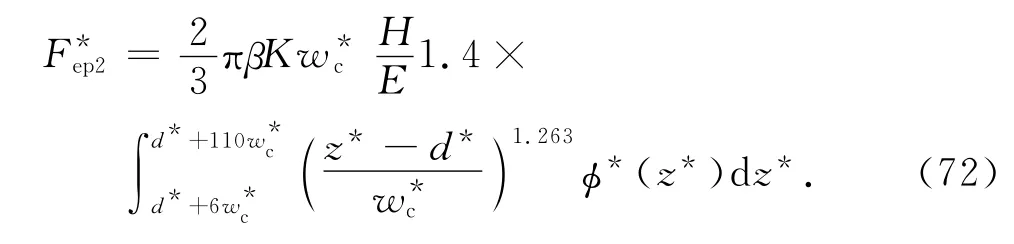
第Ⅱ彈塑性接觸剛度為

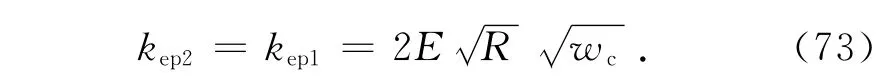
整個結合部的第Ⅱ彈塑性接觸剛度為

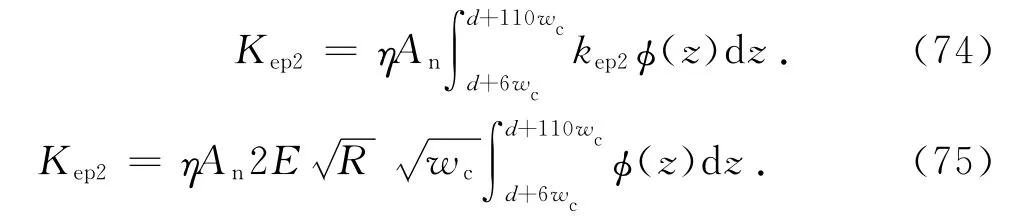
量綱為1的第Ⅱ彈塑性接觸剛度為

1.3 微接觸點的塑性變形

當w ＞110wc時，微接觸點發生塑性流動.單個微接觸點的塑性接觸面積［10］為

整個結合部的實際塑性接觸面積為

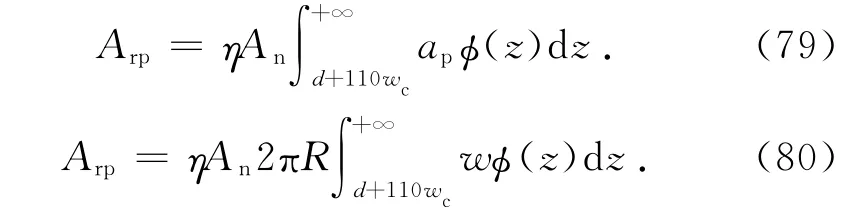
將式（1）代入式（80）得

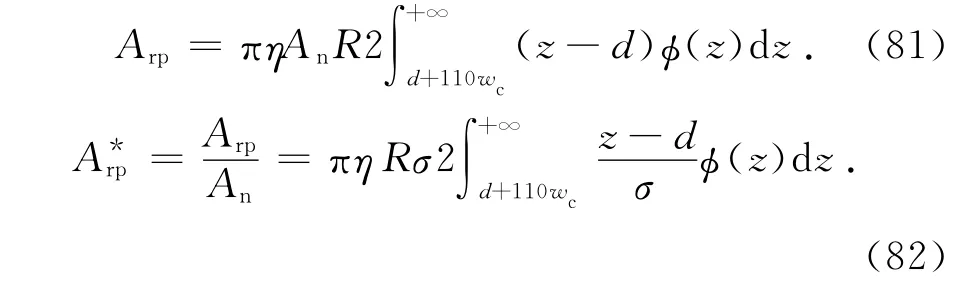
式（82）可變為［13］

單個微接觸點的塑性接觸負載［10］為

整個結合部的塑性接觸負載為

將式（1）代入式（86）得

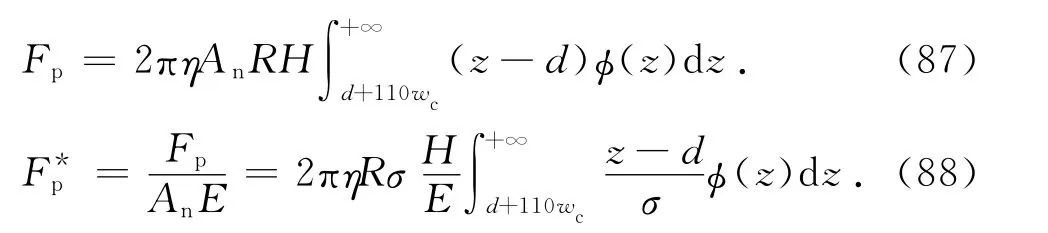
式（88）可變為［13］

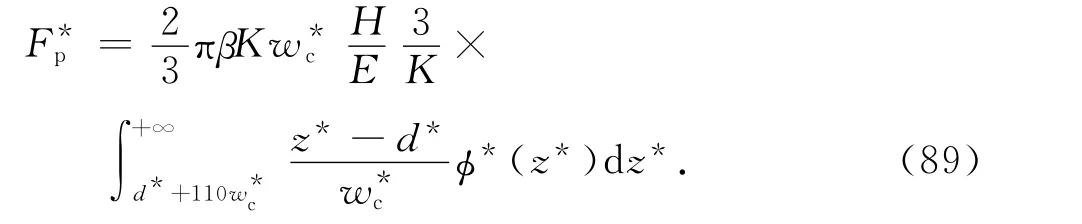
塑性接觸剛度為

整個結合部的塑性接觸剛度為

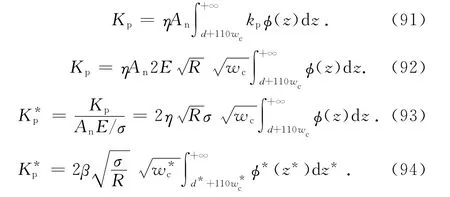
1.4 整個結合部的法向接觸參數

量綱為1的實際接觸面積為

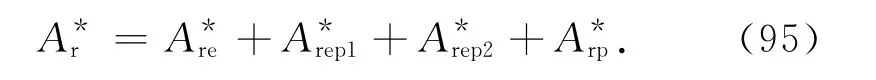
將式（9）、（34）、（65）、（83）代入式（95）得［13］

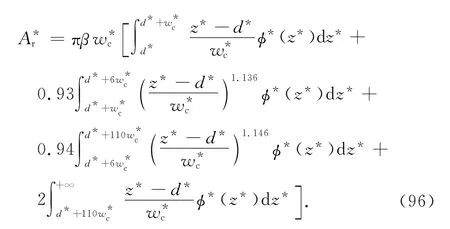
量綱為1的法向接觸負載為

將式（18）、（52）、（72）、（89）代入式（97）得［13］

量綱為1的法向接觸剛度為

將式（25）、（58）、（77）、（94）代入式（99）得

金屬制品塑性指數為

將式（16）代入式（101）得

2 地腳結合部加載的仿真

金屬地腳結合部材料采用同種材料普通碳素結構鋼Q235，參數為：E1＝E2＝2.07×1011Pa，H ＝1.96×109Pa，ν1＝ν2＝0.29.表面微觀幾何學形貌參數和待求解的塑性指數見表1.

在表1中取塑性指數ψ＝1.113 4，如圖3所示表示在微接觸點高度的3種概率密度下實際接觸面積、法向接觸負載和法向接觸剛度的比較情形.從圖3中看出，地腳結合部的實際接觸面積、法向接觸負載與法向接觸剛度都隨著混凝土地坪與標準平板之間間距的降低而增加，主要是因為混凝土地坪與標準平板之間間距的減少引起出現接觸的微接觸點的數目增多，使得實際接觸面積增加，為此需求更高的法向接觸負載，更大的法向接觸負載做功越多，地腳結合部間存儲的彈性應變能越大，法向接觸剛度上升.當間距較大時，GW 理論過高預測法向接觸參數，當d＊＝4時，GW 理論比本文大5個數量級.除了在d＊＝0和d＊＝4兩端附近區域外，在間距的正常范圍內，本文預測的法向接觸參數介乎GW 理論、文獻［4］之間.

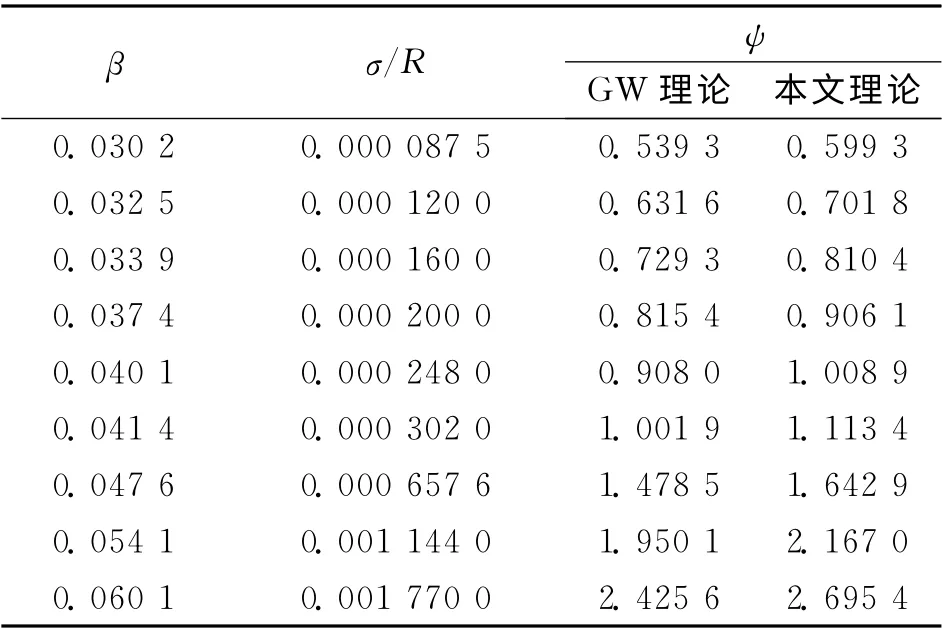
表1 涂層微觀形貌參數和導出塑性指數Tab.1 Coating micro topographical parameters and deducible plasticity indices

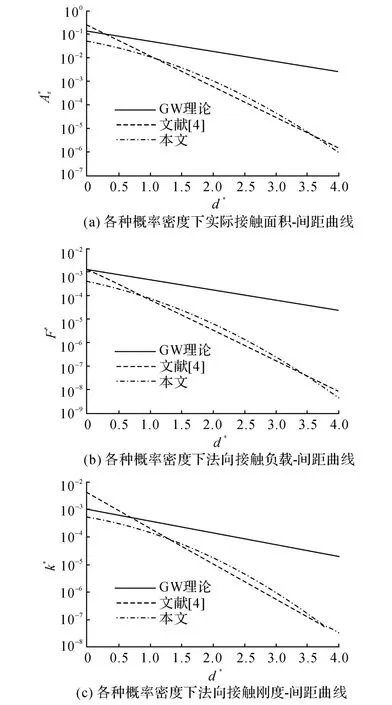
圖3 各種概率密度下法向接觸參數Fig.3 Normal contact parameters for different probability densities

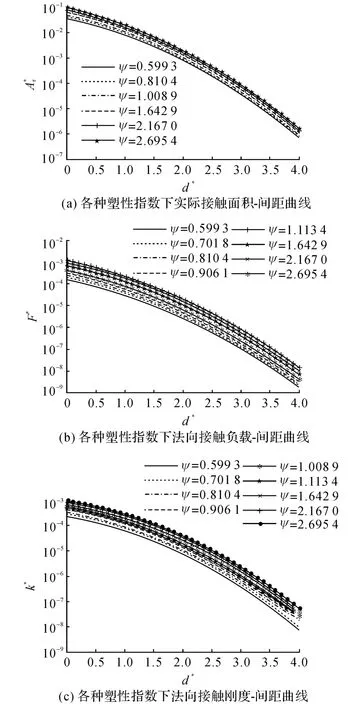
圖4 各種塑性指數下的法向接觸參數Fig.4 Normal contact parameters for diverse plasticity indexes

3 地腳結合部加載的試驗驗證

在有限元軟件ANSYS Workbench 中建立床身地腳結合部動力學模型［14］，將本文利用解析方法得到的法向接觸剛度嵌入到整體的有限元建模中.在對有限元模型進行模態分析的基礎上，進一步對仿真模型進行諧響應分析.最后對測試試件試驗、忽略地腳參數仿真、考慮地腳參數仿真3種模式下的頻率響應函數進行對比［15］，見圖5.f 為頻率.由圖5可知當考慮地腳結合部參數仿真值共振頻率與共振峰值更符合試驗值；忽略地腳結合部參數仿真值共振頻率大于試驗值，共振峰值小于試驗值.

根據三階模態試驗頻率、阻尼比和相關幾何參數，可以解算x、y、z 這3 個方向的剛度和阻尼.本文法向接觸剛度與試驗結果的對比見圖6，隨著正壓力的增大，本文法向接觸剛度曲線和z 軸法向試驗曲線走勢一致.

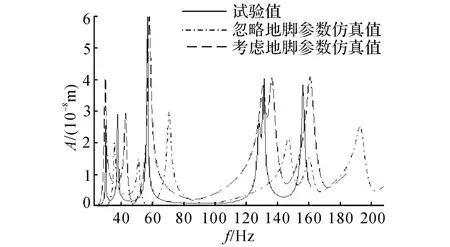
圖5 各種模式下的頻率響應函數Fig.5 Frequency response functions under distinct modes

4 結 論

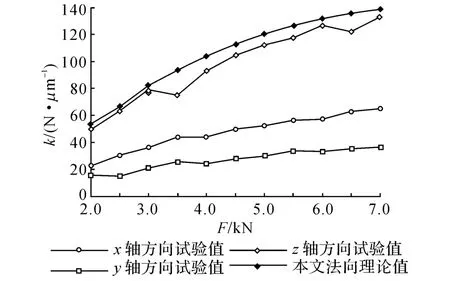
圖6 理論法向接觸剛度與試驗的對照Fig.6 Comparison of theoretical normal contact stiffness with experimental one

（1）地腳結合部的實際接觸面積、法向接觸負載與法向接觸剛度均隨著混凝土地坪與標準平板之間間距的減少而增大.

（2）地腳結合部的實際接觸面積、法向接觸負載及法向接觸剛度皆隨著塑性指數的增大而變大.

（3）通過有限元仿真的比較能夠看出，考慮了地腳參數的模型得到的諧響應分析和法向接觸剛度結果與試驗結果更為接近，間接和直接地驗證了地腳結合部法向參數辨識的準確性.

（4）單對微接觸點的法向接觸剛度等于法向接觸負載對微接觸點法向變形量的一階導函數.

（

）：

［1］葉佩青，王仁徹，趙彤，等.機床整機動態特性研究進展［J］.清華大學學報：自然科學版，2012，52（12）：1758-1763.YE Pei-qing，WANG Ren-che，ZHAO Tong，et al.Recent research advances of whole machine tool dynamics［J］.Journal of Tsinghua University：Science and Technology，2012，52（12）：1758-1763.

［2］黃玉美，付衛平，董立新，等.結合面法向動態特性參數研究［J］.機械工程學報，1993，29（3）：74-78.HUANG Yu-mei，FU Wei-ping，DONG Li-xin，et al.Research on the dynamic normal characteristic para meters of joint surface［J］.Chinese Journal of Mechanical Engineering，1993，29（3）：74-78.

［3］GREENWOOD J A，WILLIAMSON J B P.Contact of nominally flat surfaces［J］.Proceedings of the Royal Society of London：Series A Mathematical and Physical Sciences，1966，295（1442）：300-319.

［4］POLYCARPOU A A，ETSION I.Analytical approximations in modeling contacting rough surfaces ［J］.Transactions of the ASME Journal of Tribology，1999，121（2）：234-239.

［5］CHANG W R，ETSION I，BOGY D B.An elastic-plastic model for the contact of rough surfaces［J］.Transac-tions of the ASME Journal of Tribology，1987，109（2）：257-263.

［6］TIAN Hong-liang，LI Bin，LIU Hong-qi，et al.A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools［J］.Elsevier International Journal of Machine Tools ＆ Manufacture，2011，51（3）：239-249.

［7］田紅亮，方子帆，朱大林.赫茲點接觸133年［J］.三峽大學學報：自然科學版，2014，36（2）：88-97.TIAN Hong-liang，FANG Zi-fan，ZHU Da-lin.133years of Hertz point contact［J］.Journal of China Three Gorges University：Natural Sciences，2014，36（2）：88-97.

［8］左婧，徐衛亞，王環玲，等.巖石電鏡掃描圖像的分形特征研究［J］.三峽大學學報：自然科學版，2014，36（2）：72-76.ZUO Jing，XU Wei-ya，WANG Huan-ling，et al.Fractal analysis of SEM image for rocks［J］.Journal of China Three Gorges University：Natural Sciences，2014，36（2）：72-76.

［9］田紅亮，鄭金華，方子帆，等.阻尼系統的特征［J］.三峽大學學報：自然科學版，2015，37（2）：75-82.TIAN Hong-liang，ZHENG Jin-hua，FANG Zi-fan，et al.Characters of damping system［J］.Journal of China Three Gorges University：Natural Sciences，2015，37（2）：75-82.

［10］尤晉閩，陳天寧.結合面靜態接觸參數的統計模型研究［J］.振動與沖擊，2010，29（11）：47-50，252.YOU Jin-min，CHEN Tian-ning.Statistical model for static contact parameters of joint surfaces［J］.Journal of Vibration and Shock，2010，29（11）：47-50，252.

［11］ZHAO Yong-wu，MAIETTA D M，CHANG L.An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow［J］.Transactions of the ASME Journal of Tribology，2000，122（1）：86-93.

［12］KOGUT L，ETSION I.Elastic-plastic contact analysis of a sphere and a rigid flat［J］.Transactions of the ASME Journal of Applied Mechanics，2002，69（5）：657-662.

［13］KOGUT L，ETSION I.A finite element based elasticplastic model for the contact of rough surfaces［J］.Tribology Transactions，2003，46（3）：383-390.

［14］張輝，于長亮，王仁徹，等.機床支撐地腳結合部參數辨識方法［J］.清華大學學報：自然科學版，2014，54（6）：815-821.ZHANG Hui，YU Chang-liang，WANG Ren-che，et al.Parameters identification method for machine tool support joints［J］.Journal of Tsinghua University：Science and Technology，2014，54（6）：815-821.

［15］溫淑花，張宗陽，張學良，等.固定結合面剛度分形模型［J］.農業機械學報，2013，44（2）：255-260.WEN Shu-hua，ZHANG Zong-yang，ZHANG Xue-liang，et al.Stiffness fractal model for fixed joint interfaces［J］.Transactions of the Chinese Society for Agricultural Machinery，2013，44（2）：255-260.