考慮車輛超載的公路簡支梁橋疲勞性能

劉 揚，張海萍，鄧 揚，李 明

（長沙理工大學 土木與建筑學院，湖南 長沙410010）

隨著世界經濟的發展，交通量剛性需求急劇擴增，超載超限車輛占據總交通流量比例逐年增大，主要原因有以下2種：1）為追求經濟利益和運輸效率的最大化，加大車輛貨載質量，致使貨載質量大大超出原額定質量.2）設計荷載規范相對滯后.根據美國AASHO 道路試驗研究表明：汽車軸重質量與公路疲勞破壞關系為“四次方法則”.研究車輛超載對橋梁的疲勞性能影響意義重大.

超載車輛荷載統計研究方面：宗雪梅等［1］以府谷-店塔公路9種代表性運煤車為研究對象，對實測數據進行線性回歸得到車輛超載與超限的函數關系式；梅剛等［2］統計國道110車輛總重荷載概率分布呈現雙峰特征，用2個正態分布加權函數進行描述，并運用非線性最小二乘法對模型的參數進行評估計算；貢金鑫等［3-4］運用4個正態分布函數的加權分別對治超和非治超地區車輛總重概率模型進行擬合，并用極大似然估計法對參數進行評估.李彤等［5］采用極值Ⅰ型函數與2個正態分布函數加權描述得到輕車、普通車、重車的概率密度直分布圖.Gu等［6］運用貝葉斯極值分布函數擬合南京長江三橋車輛總重的直分布圖，得到概率密度函數.Miao等［7］基于動態稱重系統實測數據，分析得到香港地區車輛荷載模型.上述學者多以車輛總重或車重的荷載模型為研究對象，由文獻［1］可知，對于小跨徑橋梁而言，軸距和軸重是影響橋梁結構破壞的關鍵因素，同時也是影響建模精度的重要參數.同一輛車軸重與軸重之間不是相互獨立的隨機變量，而是存在一定的分配比例.建立協調的軸重概率模型具有一定的研究意義.

超載車輛荷載效應研究方面：Zhang等［8］對某服役43a的簡支梁橋進行實橋試驗，研究表明：橋梁在3倍30t車輛循環荷載作用下，橋梁出現明顯的線性累計損傷；Vigh 等［9］提出一種適用各種橋型的計算超載車輛荷載效應的方法；孫曉燕等［10］模擬車輛對一座服役37a的簡支T 梁橋進行為期1a的超載運營，分析表明超載運營1a對下排鋼筋造成的疲勞損傷與設計荷載作用下100a的損傷值只差一個數量級.上述文獻表明超載對于橋梁疲勞壽命影響極大，然而車輛超載率與橋梁疲勞損傷的關系表達式尚不明確.

本文以車輛超載（指貨載質量超過車輛額定載重）為研究對象，依據實測數據，在統計出車型總重概率模型的基礎上，運用剛性梁法計算各軸重分配比例，得到各軸重概率模型和車輛超載率（指車輛實際貨載重量與額定貨載重量的比值）概率模型.并推導車輛超載率與簡支梁橋疲勞損傷的關系式，結合車輛超載率與簡支梁橋疲勞損傷關系式和車輛超載概率模型，最終提出一種簡便、準確的簡支梁橋疲勞損傷計算方法.

1 車輛荷載概率建模方法

1.1 車重概率模型

一個總體樣本中包含M 個不同類的個體樣本Xi＝﹛X1，X2，…，Xm﹜，Xi為d 維隨機變量，在樣本空間中所占的比重為wi，子樣本Xi之間互為獨立變量，又第i個子樣本符合Wi（x）分布，則產生了有限混合模型：

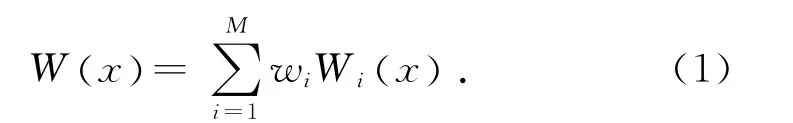
車輛不同載重率（空載、滿載和超載）形成多個個體樣本，符合有限混合模型統計原理.Wilsor［11］證明了高斯混合模型具有能夠任意逼近概率密度分布函數的能力，因此高斯混合模型能夠精確地描述多子樣本的車輛荷載概率分布，統計數據為一維空間的觀測樣本，則其概率密度表達式：

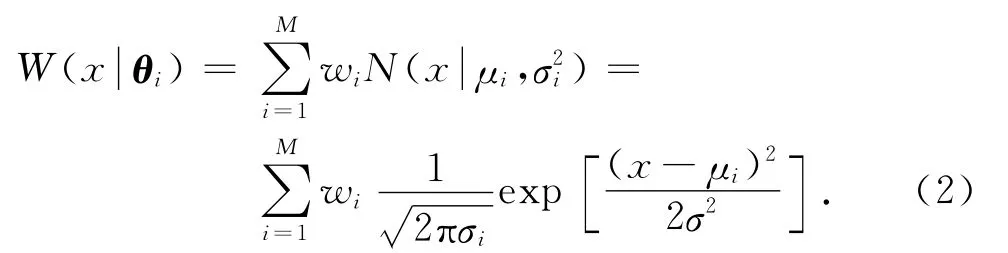
式中：x 為Xi的取值，μi 和σi2為相應的均值和方差，θi＝［w1，w2…wi；μ1，μ2…μi；σ21，σ22…σi2］.θi為式（2）參數的矩陣.

傳統單概率模型可以運用極大似然評估法對模型參數進行評估，而對于混合模型，由于缺乏已知訓練樣本的類標簽或存在部分數據缺失或不能觀測，為典型的具有不完全數據評估任務.由文獻［12］可知EM 算法對于解決典型不完全數據似然問題具有可行性.本文應用EM 算法實現對高斯混合模型的參數估計.

1.2 軸重和軸距概率模型

1.2.1 軸重概率模型 對于軸重概率模型的統計是在統計總重的概率荷載模型的基礎上參考文獻［13］中彈性支座連續梁法對輪軸荷載進行軸重分配計算，得到軸重分配系數，從而得到軸重概率統計模型：

式中：Pi（t）為車輛i軸重概率密度分布函數，ai為第i軸軸重分配系數.該方法確定軸重概率模型與直接對各軸重進行荷載統計的優點在于能夠確保模型車輛各軸重之間對應關系.若直接依據軸重統計數據建立軸重概率模型，再從模型中抽取各軸重值得到車輛模型軸重與現實車輛軸重分配比例有較大的差異，造成模擬車輛失真，影響結果精度.

1.2.2 軸距概率模型 由參考文獻［14］可知各車型軸距服從對數正態分布：

依據參考文獻［15］得其等效軸距為統計值的期望值：

式中：Se為等效軸距，S 為軸距分布函數.

2 車輛軸荷分配計算方法

將車輛車架簡化為一根剛性橫梁，輪胎和懸架均視為彈簧，在荷載作用下其變形均在線性彈性范圍內.車輛質量G 組成部分由裝載質量G1和車身質量G2組成，按照設計重心位置加載集中荷載G2到車架上，車架所受的彎矩為

式中：a為制動時車輛的加速度；mi為第i 個彈簧上的質量；Hi為第k 個支撐彈簧距車輛質心G 的距離.彈簧模型的彈性剛度為同一車軸懸架和輪胎的等效剛度：

式中：Ksi和KT分別為第i軸輪胎和懸架的垂直剛度.

結合文獻［13］和［16］進行軸荷分配計算，計算簡圖如圖1所示：

圖1 車輛軸荷分配計算簡圖Fig.1 Distribution of vehicle axle load calculation diagram

3 超載作用下梁橋疲勞壽命評估

3.1 車輛超載率與簡支梁疲勞損傷關系推導

空載重量分配至各輪軸的比例參數為ai，在車輛滿載時，貨載重量分配到各輪軸的比例參數為bi，各輪軸滿載時軸重為

則車輛超載X 倍時軸重：

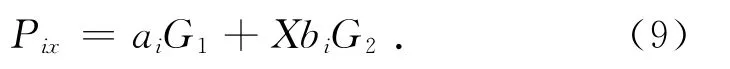
在只考慮梁截面小變形的情況下，各輪軸對橋梁結構作用為互不干擾的獨立變量，在多軸力作用下，梁跨中彎矩值為各單軸力作用對跨中產生的彎矩的累積，如圖2所示.

圖2 多軸車作用下簡支梁橋計算簡圖Fig.2 Moment of simple supported beam under vehicle axle load

在多軸車作用下，當li＜L／2 時，對支座A 取矩，支座A 反力表達式：

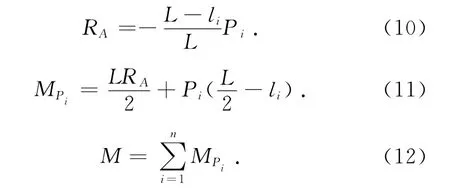
由式（10）、（11）、（12）得

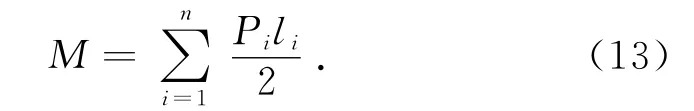
當li＞L／2時，對支座B 取矩，計算表達式同式（13）.式中RA為支座反力；L 為梁的計算跨徑；li為作用力至支座A 距離；Pi為輪軸作用力大小；MPi為單輪軸作用下跨中彎矩值；M 為多輪軸力作用下跨中的總彎矩值.同理可推導車輛超載率為X 時，簡支梁跨中彎矩表達式.

式中：β為橫向分布系數；μ 為車輛沖擊系數（為了簡化計算，車輛不同載重率下對橋梁的沖擊系數不變）；li為輪軸距較近支座的距離.

超載率X 與滿載車輛過橋對跨中底緣鋼筋產生應力幅比值：

令參數：

則超載率X 和滿載車輛過橋時結構底緣鋼筋產生應力幅比值：

材料的S-N 曲線：

在滿載情況下單輛車對橋梁造成的疲勞損傷：

超載率X 的車輛對橋梁造成的疲勞損傷：

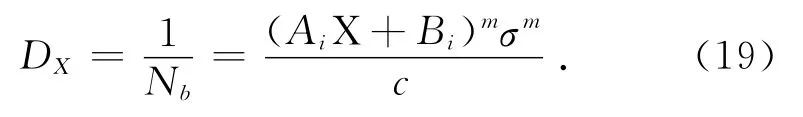
由式（18）和（19）得超載率X 的車輛相對滿載的疲勞損傷的倍數為

式（20）中軸重、軸距和橋梁跨徑確定參數Ai和Bi的取值，材料的S-N 曲線確定m 參數的取值.

3.2 簡支梁疲勞壽命評估方法

式（20）得到各代表車輛類型不同超載率與橋梁的疲勞損傷關系式，而要將其應用到公路橋梁疲勞損傷計算中，還需要做進一步的變換.首先，對荷載概率模型的變換，將各類型車重概率模型轉換成車輛超載率概率模型：

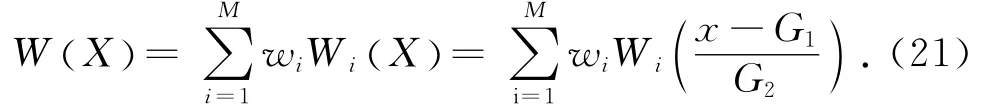
式中：X 為超載率，當X＞1時定義為車輛超載，G1為車輛空載重量，G2為車輛額定質量，x 為車重.

假設每一月有i種車型經過某橋，每種車型車量數Ni，各車型在滿載狀態下，對構件造成的疲勞損傷Dei，由式（20）可知在不同超載率狀態下，車輛對橋梁造成的疲勞損傷值為

結合式（21）和（22）得到該橋梁的月疲勞損傷計算式：

假設年交通量增長率函數為g（t），其中t為時間.則該橋梁的疲勞壽命為

基本計算流程如圖3所示：

4 實例分析

圖3 簡支梁橋疲勞損傷計算流程圖Fig.3 Assessment fatigue life flow chart of simply supported beam

基于WIM 系統對宜瀘高速南溪路段進行為期一個月的交通荷載監測統計，其每日車流量數目維持在5 000-6 500輛，車流量數目浮動范圍小，鑒于本文研究對象為疲勞車輛荷載，故過濾質量輕小客車和比重小的貨車車型.篩選得到6種典型車型，典型車型總數為27 837輛.各典型車輛所占交通流量的比重如表1所示.

表1 車型分類及比重Tab.1 Vehicle classification and proportion

表1中W 為各車型占總車流量的比重.從表中可知C2、C4、C6車輛明顯占據較大比例，而C3和C5車流量數目相對較少，呈現車“雙軸數多、單軸數少”特點.

依據文獻［1］中典型車輛的額定裝載質量和額定總質量如表2所示：

表2 典型車輛空載和額定裝載重量Tab.2 Empty weight and rated weight of type vehicle

表2中G1i和G2i分別表示第i 種車型的空載質量和貨載質量.基于實測統計數據并依據式（4）得到各軸距的統計數據如表3所示.

表3 典型車輛軸距統計Tab.3 Wheelbase of type vehicle

對統計數據進行描述得到各車型車重的概率密度P 分布函數，如圖4所示.

圖4 各車型總重概率密度分布與擬合曲線圖Fig.4 Type of vehicle weight density distribution models and fitting curves

由圖4可知，典型車輛的車荷載概率模型服從多峰分布，C2除外，其他典型運營車輛超載數量在總車流量中比例均大于50%.

各高斯混合模型的表達式參數如表4所示：

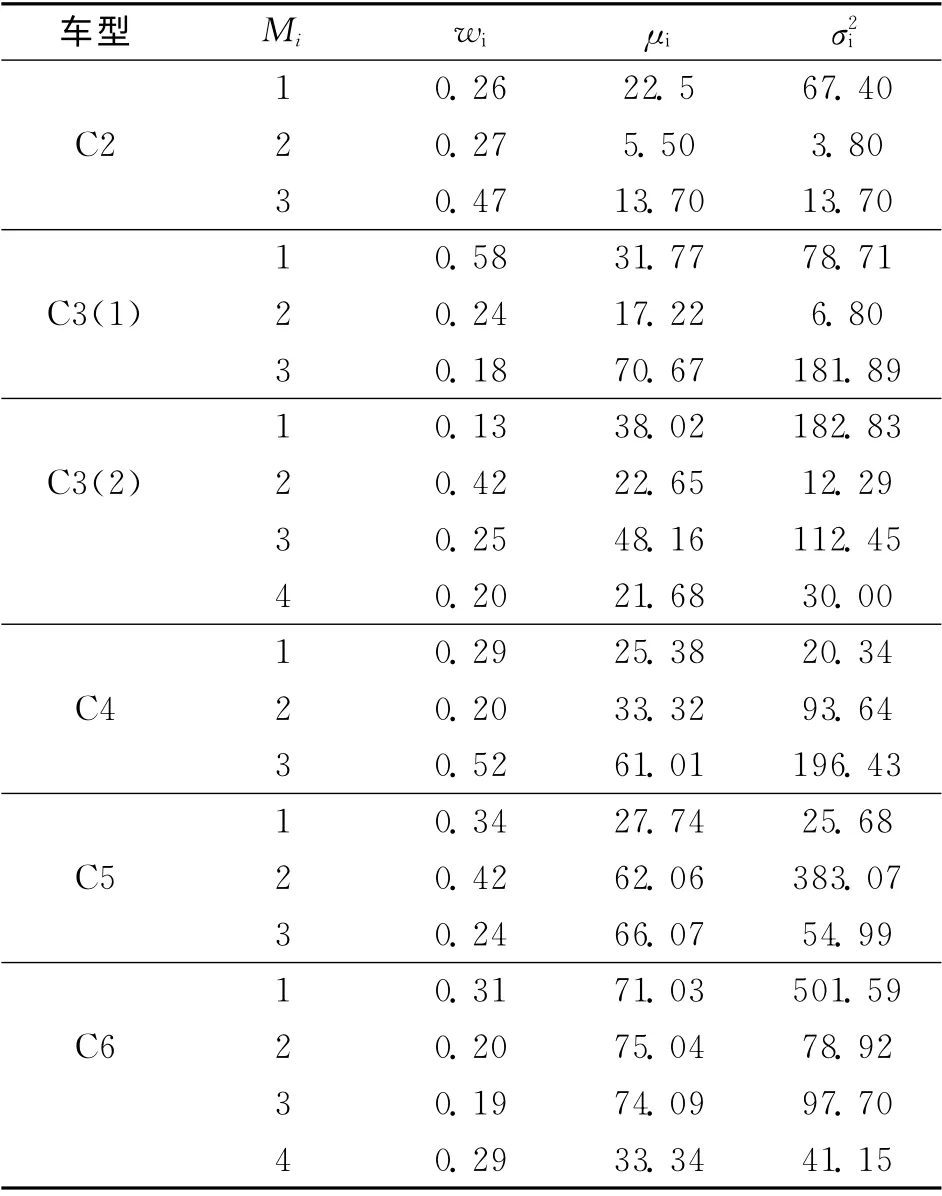
表4 車重高斯混合模型參數Tab.4 GMM parameters of vehicle weight

選用宜瀘高速某跨徑為40m 的簡支T 梁為加載對象，其基本參數：計算跨徑39.5m，公路Ⅰ級設計荷載，鋼絞線規格Φ15.2 mm2，截面具體參數值如圖5所示：

圖5 簡支T梁橫截面圖／mmFig.5 Cross section of simple supported T beam

根據文獻［13］對各車型滿載狀態下進行軸重分配計算，同時為了驗證該計算方法在本文中的適用性，將以C2車型為例，統計空載至超載400%的軸重數據與理論計算曲線如圖6所示.

由圖6可知，車輛超載率與軸重成線性關系，軸重分配理論計算曲線與實際車輛軸重統計數據能較好的擬合.由于車輛重心偏后C2隨超載率的增長，其二軸軸重增長斜率明顯大于一軸軸重.

不考慮車橋耦合振動的影響，將車輛輪軸荷載簡化為集中力，6種代表性車輛以36km／h的車速勻速過橋，在有限元軟件中進行時程分析得到跨中底緣鋼筋應力時程曲線如圖7所示.

圖6 不同超載率下C2軸重分布曲線Fig.6 Curve of C2axle load in different overload rate

圖7 C2-C6滿載車輛過橋跨中底緣鋼筋應力時程曲線Fig.7 Stress time-history curves of edge Reinforcement bars under vehicle load of C2-C6

得到各車型在滿載狀態下單次過橋的結構跨中底緣鋼筋的應力幅，并依據參考文獻［17］中變形鋼筋S-N 曲線參數得到各車型對梁橋結構產生的損傷值，如表5所示.

表5 車輛滿載作用下跨中底緣鋼筋應力幅值與損傷值Tab.5 Bottom edge of reinforced stress amplitude and damage values under vehicle fully loaded

△σi為底緣鋼筋應力幅值，依據2.1節計算推導過程以及實測統計數據計算參數Ai和Bi如表6所示，m 值依據材料S-N 曲線均取值3.

表6 典型車輛參數Ai 和Bi 計算值Tab.6 Parameters A and B of typical vehicle

依據式（21）及表5 和6 計算參數，筆者使用matlab數值分析軟件中trapz功能函數進行定積分計算得到橋梁的月疲勞損傷值為5.8×10-6.參考文獻［18］假設交通量年增長率為5%，在不考慮外界環境因素，車輛荷載作用下橋梁的疲勞壽命為88年，結構疲勞損傷發展曲線如圖8所示.

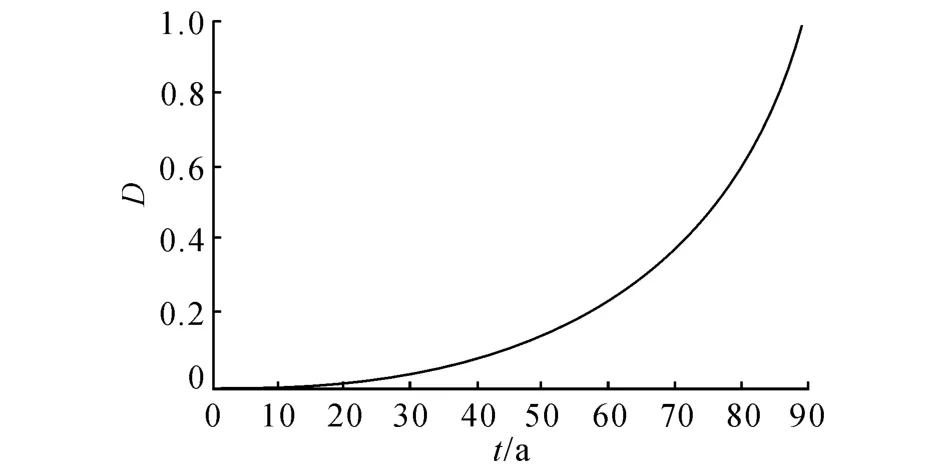
圖8 橋梁疲勞損傷發展曲線Fig.8 Developmental curve of bridge fatigue damage

5 結 論

（1）推導了車輛超載率與鋼筋混凝土簡支梁橋疲勞損傷倍數的關系式，可知車輛超載對結構疲勞損傷影響顯著.

（2）建立了車輛超載率概率模型，并將超載率與梁橋疲勞損傷倍數關系式應用于工程實際橋梁的疲勞損傷壽命評估中，以車輛超載率為切入點，提出了一種新的簡支梁橋疲勞損傷計算方法.

（3）基于WIM 系統對宜瀘高速南溪長江大橋路段進行交通調查統計，得到了6種典型車輛超載率概率模型.在此基礎上，依據所提出的疲勞損傷計算方法對宜瀘高速某簡支梁的疲勞壽命進行了評估，其疲勞壽命為88a.

（

）：

［1］宗雪梅，胡大琳，高軍.橋梁超重荷載與限載標準的確定［J］.長安大學學報：自然科學版，2008，28（1）：60-65.ZONG Xue-mei，HU Da-lin，GAO Jun.Vehicle’s overloadand limiting load standard for bridge safety ［J］.Journal of Chang’an University：Science and Technology，2008，28（1）：60-65.

［2］梅剛，秦權，林道錦.公路橋梁車輛荷載的雙峰分布概率模型［J］.清華大學學報：自然科學版，2003，43（10）：1394-1396.MEI Gang，QIN Quan，LIN Dao-jin.Bi-modal probabilistic model of highway and bridge vehicle loads［J］.Tsinghua University：Science and Technology，2003，43（10）：1394-1396.

［3］貢金鑫，李文杰，趙君黎，等.公路橋梁車輛荷載概率模型研究（一）——非治超地區［J］.公路交通科技，2010，27（6）：40-45.GONG Jin-xin，LI Wen-jie，ZHAO Jun-li，et al.Research on probabilistic model of high-way bridge vehicle loads（1）—non-controlling area［J］.Journal of Highway and Transportation Research and Development，2010，27（6）：40-45.

［4］貢金鑫，李文杰，趙君黎，等.公路橋梁車輛荷載概率模型研究（二）——計重收費地區和強制治超地區［J］.公路交通科技，2010，27（7）：56-60.GONG Jin-xin，LI Wen-jie，ZHAO Jun-li et al.Research on probabilistic model of high way bridge vehicle loads（2）—controlling Area［J］.Journal of Highway and Transportation Research and Development，2010，27（6）：40-45.

［5］郭彤，李愛群，趙大亮.用于公路橋梁可靠性評估的車輛荷載多峰分布概率模型［J］.東南大學學報：自然科學版，2008，38（5）：763-766.GUO Tong，LI Ai-qun，ZHAO Da-liang.Multiple–peaked probabilistic vehicle load model for highway bridge reliability assessment［J］.Journal of Southeast University：Science and Technology，2008，38（5）：763-766.

［6］GU Y，LI S，LIH，et al.A novel Bayesian extreme value distribution model of vehicle loads incorporating decorrelated tail fitting：Theory and application to the Nanjing 3rd Yangtze River Bridge［J］.Engineering Structures，2014，59：386-392.

［7］MIAO T J，CHANT H T.Bridge live load models from WIM data［J］.Engineering Structures，2002，24（8）：1071-1084.

［8］ZHANG J，PENG H，CAI C S.Field study of overload behavior of an existing reinforced concrete bridge under simulated vehicle loads［J］.Journal of Bridge Engineering，2010，16（2）：226-237.

［9］VIGH A，KOLLAR L P.Approximate analysis of bridges for the routing and permitting procedures of overweight vehicles［J］.Journal of Bridge Engineering，2006，11（3）：282-292.

［10］孫曉燕，王海龍.超載運營下服役鋼筋混凝土橋梁疲勞損傷研究［J］.應用基礎與工程科學學報，2008，16（5）：733-740.SUN Xiao-yan，WANG Hai-Long.Fatigue damage anlysis on esting reinforced Concrete bridge under over-loading［J］.Journel of Basic Science and Engineering，2008，16（5）：733-740.

［11］WILSON R G.Multiresolution Gaussian mixture models：theory and application［J］.Computer Science and Repository，2000.

［12］NG H K T，CHAN P S，BALAKRISHNAN N.Estimation of parameters from progressively censored data using EM algorithm［J］.Computational Statistics ＆Data Analysis，2002，39（4）：371-386.

［13］王興東，楊波，鄒光明.多軸汽車軸荷分配和轉移的計算方法研究［J］.湖北工業大學學報，2006，21（3）：165-167.WANG Xing-dong，YANG Bo，ZOU Guang-ming，Comuting methods for distribution and transfer of multiaxle vehicles vertical axle Loads［J］.Journal of Hubei University of Technology，2006，21（3）：165-167.

［14］GUO T，FRANGOPOL D M，CHEN Y.Fatigue reliability assessment of steel bridge details integrating weigh-in-motion data and probabilistic finite element analysis［J］.Computers ＆Structures，2012，112：245-257.

［15］孫守旺，孫利民.基于實測的公路橋梁車輛荷載統計模型［J］.同濟大學學報：自然科學版，2012，40（2）：198-204.SUN Shou-wang.SUN Li-min.Statistic model of vehicle loads for highway bridges［J］.Journal of Tong Ji University：Science and Technology，2012，40（2）：198-204.

［16］龍馭球.結構力學［M］.北京：高等教育出版社，1994：254-427.

［17］曾志斌，李之榕.普通混凝土梁用鋼筋的疲勞S-N 曲線研究［J］.土木工程學報，1999，32（5）：10-14.ZENG Zhi-bin，LI Zhi-rong.Research on fatigue S-N curves of reinforcing bars in common reinforced concrete beams［J］.China Civil Engineering Journal，1999，32（5）：10-14.

［18］王春生，周江，吳全有，等.既有混凝土橋梁疲勞壽命與使用安全評估［J］.中國公路學報，2012，25（6）：101-107.WANG Chun-sheng，ZHOU Jiang，WU Quan-you，et al.Fatigue life and service safety assessment for existing concrete bridges［J］.China Journal of Highway and Transport，2012，25（6）：101-107.