考慮受電弓系統的高速列車氣動噪聲分析

羅 樂，鄭 旭，呂 義，郝志勇

（1.浙江大學 能源工程學系 浙江 杭州310027；2.長春軌道客車股份有限公司 吉林 長春130000）

我國的高鐵產業正在蓬勃發展，但隨著運行時速的提升，高速列車的噪聲問題日益突出并引起廣泛關注.大量的試驗研究［1-3］表明，氣動噪聲的增長速度約為運行速度的6次方，是列車高速運行時的主要噪聲源.因此對氣動噪聲進行研究和控制是解決高速列車噪聲問題的重要課題之一.

高速列車的氣動噪聲是典型的流體聲學問題，該領域的理論基礎是經典Lighthill聲學比擬理論.隨著計算機技術的發展，諸如直接數值模擬（DNS）、大渦模擬（LES）、非定常雷諾平均模擬（URNS）等數值計算方法也越來越多地被用于高速列車氣動噪聲的研究工作中.Takehisa等［4］基于大渦模擬與緊致Green函數相結合的方法研究了高速列車受電弓弓角表面的偶極子噪聲源，并分析了弓角表面穿孔對氣動噪聲的降噪原理；Xiao等［5］采用二維大渦模擬和lighthill-Curle理論研究了高速列車頭部縱向對稱面上的氣動噪聲，并結合Nurbs曲線對頭部型線進行了低噪聲設計；劉加利等［6］基于標準κ-ε 湍流模型和寬頻帶噪聲源模型研究了高速列車車頭表面氣動噪聲源的頻譜特性，同時結合大渦模擬與FW-H聲學模型分析了遠場氣動噪聲的分布規律；孫振旭等［7］分別采用非線性聲學求解方法和FW-H 方程計算了CRH3型高速列車近場與遠場的氣動噪聲特性，并對關鍵部位的噪聲水平進行了綜合評估.

目前高速列車的氣動噪聲研究還主要集中在頭尾車及中間車組的車廂表面，而對于受電弓等結構復雜且突出的部位關注相對較少.鑒此，本文擬結合大渦模擬和聲學邊界元方法對帶有受電弓的高速列車車廂表面的不同氣動噪聲源進行數值計算，并對比分析頻譜特性和分布規律.

1 基本理論

1.1 氣動聲學方程

Lighthill根據N-S 方程和連續性方程推導了經典的氣動聲學傳播方程［8］：

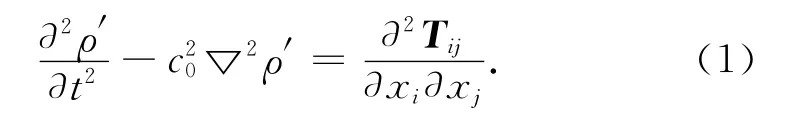
其中：

式中：Tij為Lighthill張量；eij為黏性應力張量；δij為單位張量；▽2為拉普拉斯算子；ρ′為流體密度的擾動量；p′為流場中壓力的脈動量；μ 為湍流黏性系數；ui、uj、uk分別為空氣速度分量；xi、xj、xk分別為直角坐標分量；ρ為流體密度；c0為聲速；t為時間.

1.2 湍流模型

本文采用大渦模型計算流場作用在結構表面的脈動壓力，其基本理論是將湍流脈動劃分為大小尺度2部分.其中大尺度脈動通過求解濾波后的N-S方程得到，而通過構建濾波產生的亞格子尺度應力來體現小尺度脈動對流場的影響［9］.控制方程為

為使方程封閉，采用渦旋黏性模型構造τij的數學表達式：

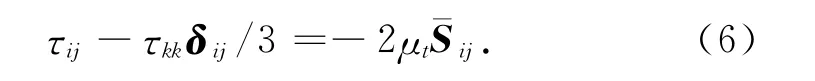
1.3 聲學邊界元

將脈動壓力作為氣動載荷的邊界條件，然后計算其聲場分布，本文采用直接邊界元法，聲場壓力應滿足Helmholtz方程：

式中：p（x，y，z）為聲場壓力；q（x，y，z）為單位體積的體積速度；m 為波數；ω 為角頻率.

直接邊界元［10］就是對邊界積分方程進行求解，外部輻射聲場中任意一點x 處的聲壓與聲源表面S（y）上聲壓和聲壓梯度值之間的關系為

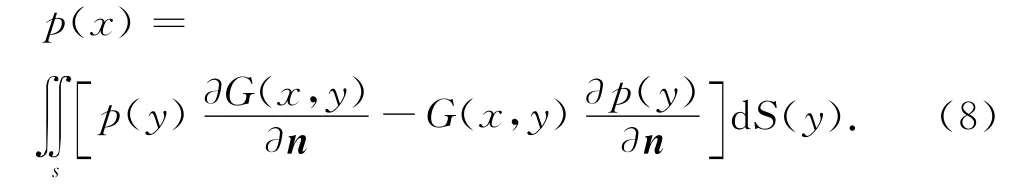
式中：p（x）和p（y）分別代表x 和y 點的聲壓；n 為S 面上的法線向量；G（x，y）為格林函數.

本文的研究對象是CRH3 型高速列車的一節帶受電弓系統的車廂（以下簡稱2號車廂）.由于整車的車廂結構與受電弓的細桿結構對流體網格的尺寸要求差別較大，如果放在同一個風洞模型中，則會大幅增加流體網格的數量和計算求解的時間，且網格質量和仿真精度較難保證，因此對受電弓系統和車廂主體分別進行建模和求解.

2 受電弓氣動噪聲計算

2.1 風洞模型

受電弓作為2號車廂車頂上的突出部件，棱角、凹凸面、空隙等幾何特征十分顯著.考慮到網格劃分的簡易性，同時保留其主要的氣動特性，幾何建模時忽略了升弓彈簧、傳動氣缸和平衡桿等部件，簡化后的受電弓模型主要包括了絕緣子、底架、下臂桿、推桿、上臂桿和雙滑板等，如圖1所示.受電弓系統的風洞模型如圖2所示，主要包括受電弓、導流罩、進風口、出風口以及風洞壁面等.風洞的計算域應該足夠大以消除尾流的影響，尺寸為14.8m×5.9m×9.8m.計算域的網格劃分采用三角形面單元和四面體單元，其中受電弓表面網格的最小尺寸為10 mm，整個計算模型的網格總量約為760萬.

風洞模型的邊界條件定義如下：入口速度為350km／h，出口壓力為1 個標準大氣壓，其余邊界均設為剛性壁面.外部流場的計算分為2步：首先采用標準κ-ε湍流模型計算受電弓系統的穩態流場，然后將穩態結果作為初始條件，采用大渦模擬繼續計算瞬態流場，進而獲得受電弓表面的脈動壓力.瞬態計算時，時間步長設為0.5×10-4s.時間步數設置為4 000 步，可保證空氣流經整個計算域.

圖1 受電弓幾何模型Fig.1 Geometry model of pantograph

圖2 受電弓風洞模型Fig.2 Wind tunnel model of pantograph

2.2 流場旋渦瞬時云圖分析

在列車高速行駛時，受電弓各部件會對氣流產生嚴重的擾動，導致不同尺度的旋渦形成、脫落及破碎，最終轉化為氣動噪聲.為了說明這一現象，從大渦模擬的計算結果中特別選取了3個監測面上的流場旋渦瞬時云圖，如圖3 所示，監測面參數z＝0、0.55、-0.55m 分別代表受電弓中心及兩側絕緣子在流速方向上的中心軸截面.云圖上的顏色越亮，代表渦量強度越大.

已知渦量是速度場旋度的度量.旋渦不僅隨時間產生、發展、衰減、消失，還會從渦量強度大的地方向渦量強度小的地方擴散，直至渦量強度均衡為止［11］.當z＝0m 時，受電弓表面旋渦最明顯的位置從上到下分別對應著雙滑板弓頭、上下臂桿和推桿的鉸接處、前端底架與推桿連接處、后端底架與下臂桿連接處，以及中心絕緣子表面等區域.類似地，當z＝0.55m 和z＝-0.55m 時，在雙滑板的弓角表面以及監測面對應的絕緣子表面旋渦最明顯.以上區域容易形成較大的脈動壓力，是受電弓結構表面的主要氣動噪聲源.

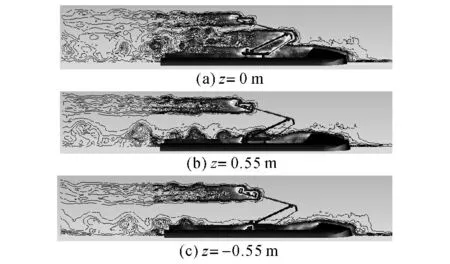
圖3 3個監測面上的流場旋渦瞬時云圖Fig.3 Transient contours of vortices on three monitor planes

2.3 聲學邊界元模型及結果分析

將大渦模擬計算得到的受電弓表面脈動壓力作為氣動噪聲源，利用直接邊界元法計算其外輻射聲場，同時建立車廂表面場點模型，可得到氣動噪聲在近場受電弓表面和遠場車廂表面的分布，分析模型如圖4所示.已知流場中的氣動噪聲源主要分為單極子聲源、偶極子聲源和四級子聲源3種.對于高速列車而言，將其表面看作是剛性的，體積脈動量幾乎為0，單極子聲源可以忽略；而四級子聲源與偶極子聲源強度之比正比于馬赫數的平方.高速列車以350km／h的速度運行時，其馬赫數約為0.286，說明四級子聲源遠小于偶極子聲源，也可不必考慮.所以本文在進行聲學計算時將氣動噪聲源定義為偶極子聲源.由1／6波長原理［12］可知，受電弓的邊界元網格尺寸最大取28mm 時，可滿足2 000 Hz以內的聲學計算精度.

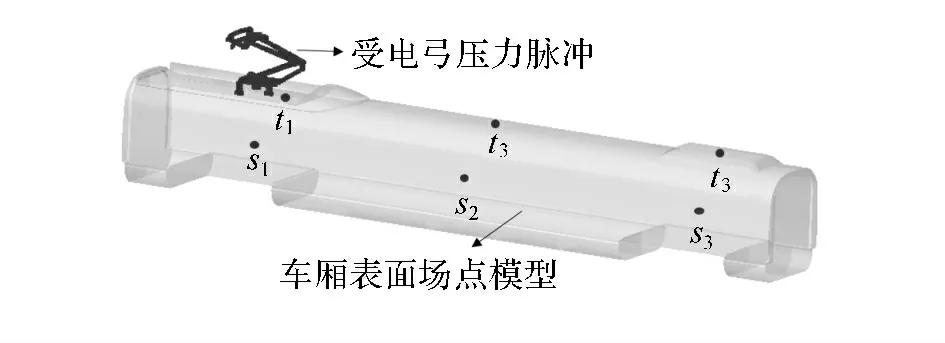
圖4 受電弓氣動激勵下的聲學邊界元分析模型Fig.4 Acoustic boundary element model for aerodynamic excitation of pantograph

在計算完成后，首先觀察受電弓表面氣動噪聲源的分布情況，如圖5所示為不同特征頻率f 下的聲壓級SPL 分布云圖.可以發現，受電弓表面聲壓級幅值較大的區域均集中在絕緣子、底架、上下臂桿與推桿的鉸接處，以及雙滑板弓頭與弓角等位置.以上位置的聲壓級較大，說明脈動壓力也較大，這與圖3流場旋渦瞬時云圖中反映的現象是一致的.另外隨著頻率的升高，氣動噪聲的分布情況變化不大，但幅值上呈降低趨勢，其中最大聲壓級從100Hz時的145dB下降到1 000 Hz時的114dB，形成了約30 dB的聲壓級差.

圖5 受電弓脈動壓力在表面形成的氣動噪聲源Fig.5 Aerodynamic noise source caused by fluctuating pressure of pantograph

受電弓的氣動噪聲源在車廂表面形成的聲激勵屬于遠場噪聲，其聲壓級分布云圖如圖6所示.可以看到，聲激勵集中分布在距離受電弓絕緣子較近的車廂頂部，并以此為中心向車廂壁面擴散，導致在受電弓導流罩、車廂后端的側面與車窗表面等位置均有不同程度的體現.相對而言，在遠離受電弓區域的車廂表面，氣動噪聲激勵并不明顯.對比100 和1 000Hz下的云圖還可以發現，低頻段聲激勵的幅值較大，且分布較集中；中高頻段聲激勵的幅值明顯降低，但擴散區域更廣，影響范圍更大.

圖6 受電弓氣動噪聲在車廂表面形成的聲激勵Fig.6 Acoustic excitation on coach surface caused by aerodynamic noise of pantograph

為了進一步說明聲激勵的頻譜特性和分布規律，如圖4所示在車廂表面布置6個觀察點，并提取每個觀察點的聲壓級頻譜.圖中t1、t2、t3分別代表頂面后端（靠近受電弓）、中心和前端觀察點，s1、s2、s3分別代表側面后端、中心和前端觀察點.

聲壓級頻譜SPL如圖7所示，受電弓的氣動噪聲源在車廂表面形成的聲激勵沒有明顯的峰值主頻率，是一種寬頻噪聲；低頻段的聲激勵幅值較大，占聲壓級總值的比重較高；各觀察點的頻譜變化趨勢一致，均是隨著頻率f 的升高，幅值持續下降，且500Hz以內的下降趨勢更明顯，500 Hz以上的趨勢較平緩；t1與t2之間、s1與s2之間分別形成了約15和12dB的聲壓級差，而t2和t3之間、s2和s3之間的頻譜相差較小，這說明受電弓的脈動壓力對車廂表面的聲激勵主要分布在車廂后端，而在車廂中部和前端等距離受電弓較遠的區域，聲激勵已有較大幅度的下降，且差異性越來越小.

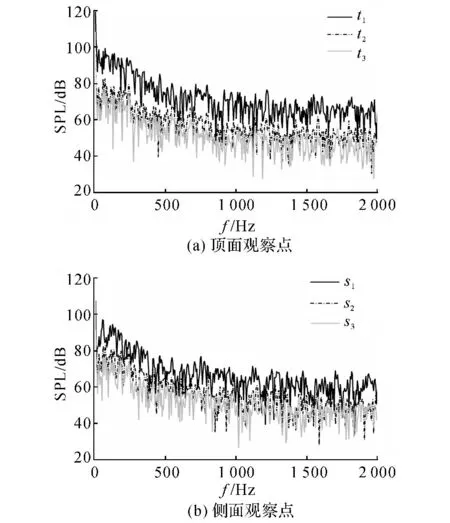
圖7 受電弓氣動激勵下的聲壓級頻譜Fig.7 SPL spectrum excited by aerodynamic noise of pantograph

3 氣動噪聲對比分析

3.1 車廂氣動噪聲計算

為了計算2號車廂氣動噪聲源在表面形成的聲激勵，根據本文第2節的計算思路，首先搭建車廂的風洞模型如圖8所示，包括進風口、頭車、2號車廂、尾車、風洞壁面和出風口等.頭車和尾車的主要作用是保證2號車表面的流場較為順暢，風洞計算域的具體尺寸為150m×15m×15m.計算域同樣由三角形面單元和四面體單元組成.由于研究主體是2號車廂，為了縮減計算時間，網格劃分時對其表面及周邊區域進行了細化，車廂表面網格的最小尺寸為50mm.而頭車和尾車及其流場區域的網格較粗，整個計算模型的網格總量約為640萬.

進風口和出風口的邊界條件與受電弓風洞模型的設置保持一致，各車廂表面定義為剛性壁面.為了模擬地面效應，將風洞底面設置為滑動壁面，滑動速度與來流速度相同，即350km／h.其余風洞壁面定義為對稱邊界.脈動壓力的計算同樣分兩步進行，其中瞬態計算的時間步長設為2.5×10-4s，時間步數為6 400 步.

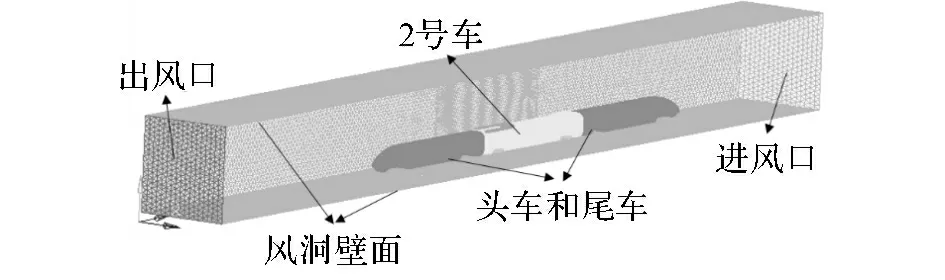
圖8 車廂風洞模型Fig.8 Wind tunnel model of coach

將大渦模擬計算得到的車廂表面脈動壓力作為偶極子噪聲源，并利用直接邊界元法進行聲學響應計算，得到氣動噪聲在車廂表面的近場分布.如圖9所示為2個特征頻率下的聲壓級分布云圖.與受電弓氣動激勵下的分布情況相比，車廂脈動壓力形成的氣動噪聲源分布更加均衡.其中聲壓級較大的位置集中在受電弓導流罩及其包圍面、空調導流罩四周以及轉向架和車體連接處等區域.這些區域有的存在結構突變，有的表面不平整，當空氣流過時會受到較大的阻礙，導致流場的平順性被破壞，流場與車體表面的作用加劇，進而產生明顯的脈動壓力，并形成氣動噪聲源.另外對比100和1 000Hz下的云圖還可以發現，單個氣動噪聲源在低頻時的作用面積較集中，而高頻時較分散.

圖9 車廂脈動壓力在表面形成的氣動噪聲源Fig.9 Aerodynamic noise source caused by fluctuating pressure of coach

同樣地取圖4中的6個場點作為聲壓級頻譜的觀察點，根據之前的云圖分析可知，所選場點中只有t1處于車廂表面氣動激勵較大的區域，其它觀察點所處的位置聲壓級較為均勻.如圖10所示，聲激勵的頻譜結果也印證了這一分布規律，其中側面觀察點s1、s2、s3的聲壓級頻譜高度一致，而頂面觀察點中僅t1在500 Hz以前的聲壓級明顯偏大，其余頻段的一致性較好.已知t1位于受電弓導流罩前端下行面與車廂頂面的交接處，該處存在明顯的旋渦運動，并沿列車的縱向與兩側延伸和發展，類似于圖3中的瞬時云圖現象，這也是導致t1觀察點聲壓級較大的原因.另外從頻域上來看，300 Hz以下的低頻段聲激勵頻譜急劇下降，300～1 500 Hz頻段內在66dB附近波動，再之后聲壓級先下降直到在1 600 Hz左右開始呈增長趨勢.

圖10 車廂氣動激勵下的聲壓級頻譜Fig.10 SPL spectrum excited by aerodynamic noise of coach

3.2 2種氣動噪聲對比

本文計算了2種氣動噪聲，一種是受電弓脈動壓力經空氣傳播后在車廂表面形成的遠場氣動噪聲，另一種是車廂脈動壓力在表面形成的近場氣動噪聲.對同一測點下的聲激勵進行對比，結果如圖11所示.考慮到人的主觀聽覺感受，對聲壓級頻譜作A計權并取對數坐標.圖中tp為受電弓氣動激勵，tc為車廂氣動激勵.

圖11（a）、（d）分別為車廂后端觀察點t1和s1的A 聲級頻譜對比，可以看到在不同的頻段上氣動噪聲的頻譜特性也有所不同.其中在60 Hz以下的低頻段車廂氣動激勵遠大于受電弓氣動激勵；60～600Hz頻段內受電弓氣動激勵會略高過車廂氣動激勵；而在600 Hz以上頻段兩者相差較小，僅在1 600Hz以后車廂氣動激勵開始上升而重新占主導.當觀察點移至車廂中部的t2和s2時，由于距離受電弓區域較遠，受電弓的氣動激勵會有較大幅度的下降，但同時車廂氣動激勵變化并不大，因此對比結果如圖11（b）、（e）所示，在60和100 Hz以下的低頻段以及600Hz以上的中高頻段內均是車廂氣動激勵占主導，而受電弓的氣動噪聲幅值僅在低頻向中高頻的過度頻段內與前者相當.最后隨著觀察點進一步遠離至車廂前端時，受電弓的氣動激勵幾乎在整個分析頻段內（10～2 000Hz）都比車廂氣動激勵小，如圖11（c）、（f）所示.由此可見，距離受電弓區域越遠，受電弓的氣動噪聲下降明顯，占總氣動噪聲的比重越低.

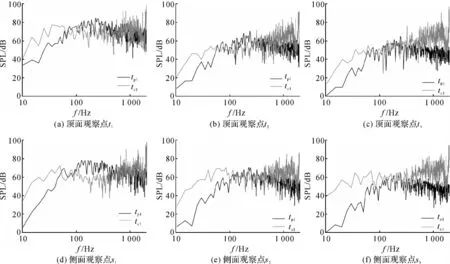
圖11 不同氣動噪聲的A聲級頻譜對比Fig.11 A-weighted SPL spectrum comparison of different aerodynamic noise

4 結 論

本文結合大渦模擬和直接邊界元法對CRH3型高速列車在350km／h運行速度下的氣動噪聲進行了研究，并分別考慮受電弓和車廂的氣動激勵，得到車廂表面氣動噪聲的頻譜特性和分布規律：

（1）受電弓在雙滑板弓頭及弓角、上下臂桿和推桿的鉸接處、底架與推桿和下臂桿的連接處以及絕緣子表面等區域的旋渦運動最明顯，是主要的氣動噪聲源.

（2）受電弓氣動激勵無明顯的峰值主頻率，是一種寬頻噪聲.低頻段的激勵幅值較大，且集中分布在車廂端部；中高頻段的激勵幅值明顯降低，但擴散區域更廣.

（3）車廂氣動激勵的分布比較均衡，主要作用于車廂表面不平整的位置.聲激勵頻譜在300Hz以下急劇下降，300～1 500 Hz頻段內平緩波動，再之后先下降直到1 600Hz左右開始呈上升趨勢.

（4）在車廂后端，受電弓的氣動激勵幅值僅在低頻向中高頻的過渡頻段上略高過車廂氣動激勵.隨著與受電弓區域距離的增加，受電弓氣動噪聲占總氣動噪聲的比重越來越低.

（

）：

［1］MELLET C，LéTOURNEAUX F，POISSON F，et al.High speed train noise emission：Latest investigation of the aerodynamic／rolling noise contribution［J］.Journal of Sound and Vibration，2006，293（3／5）：535-546.

［2］TALOTTE C，GAUTIER P E，THOMPSON D J，et al.Identification，modelling and reduction potential of railway noise sources：a critical survey［J］.Journal of Sound and Vibration，2003，267（3）：447-468.

［3］NOH H M，CHOI S，HONG S，et al.Investigation of noise sources in high-speed trains［J］.Proceedings of the Institution of Mechanical Engineers，Part F：Journal of Rail and Rapid Transit，2014，228（3）：307-322.

［4］TAKAISHI T，IKEDA M，KATO C.Method of evaluating dipole sound source in a finite computational domain［J］.Journal of the Acoustical Society of America，2004，116（3）：1427-1435.

［5］XIAO Y G，YANG Q，SUN L，et al.Longitudinal type-line optimization of high-speed train for low aerodynamic noise［J］.Journal of Central South University，2014（06）：2494-2500.

［6］劉加利，張繼業，張衛華.高速列車車頭的氣動噪聲數值分析［J］.鐵道學報.2011（09）：19-26.LIU Jia-li，ZHANG Ji-ye，ZHANG Wei-hua.Numerical analysis on aerodynamic noise of the high-speed train head［J］.Journal of the CHINA Railway Society，2011（09）：19-26.

［7］孫振旭，宋婧婧，安亦然.CRH3型高速列車氣動噪聲數值模擬研究［J］.北京大學學報：自然科學版，2012（05）：701-711.SUN Zhen-xu，SONG Jing-jing，AN Yi-ran.Numerical simulation of aerodynamic noise generated by CRH3 high speed train［J］.Acta Scientiarum Naturalium Universitatis Pekinensis，2012（05）：701-711.

［8］馬大猷.現代聲學理論基礎［M］.北京：科學出版社，2004：296-306.

［9］張兆順，崔桂香，許春曉.湍流理論與模擬［M］.北京：清華大學出版社，2005：236-263.

［10］BRANCATI A，ALIABADI M H.Boundary element simulations for local active noise control using an extended volume［J］.Engineering Analysis with Boundary Elements，2012，36（2）：190-202.

［11］YU H H，LI J C，ZHANG H Q.On aerodynamic noises radiated by the pantograph system of high-speed trains［J］.Acta Mechanica Sinica，2013，29（3）：399-410.

［12］PAPADOPOULOS C I.Development of an optimised，standard-compliant procedure to calculate sound transmission loss：numerical measurements［J］.Applied Acoustics，2003，64（11）：1069-1085.